Применение производной. Нахождение наибольшего и наименьшего значения функции на отрезке. Алгебра .10 класс.

Применение производной.

Тема № 6. Нахождение наибольшего и наименьшего значения функции на отрезке.

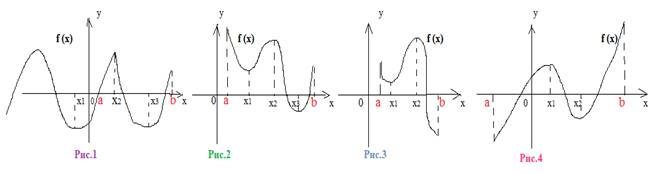
Краткая теоретическая часть (конспект вместе с разобранными примерами). Рассмотрим, как производная используется для нахождения  наибольшего  и наименьшего значения функции  на отрезке. Наибольшее и наименьшее значение непрерывной функции на отрезке может быть как на концах отрезка, так и внутри него. ( в отличие от  экстремумов функции, которые на концах промежутка не могут быть). Если наибольшее или наименьшее значение достигается внутри отрезка, то это только в стационарных точках (где производная равна нулю)  или в критических ( где производная не существует). Будем их называть одним словом «Критические». Рассмотрим рисунки.

 Рис.1.  На отрезок [a;b] попадают две  критические точки (Х₂ и Х₃). В точке Х₂   будет наибольшее значение, в точке Х₃ - наименьшее. В данном случае наибольшее значение совпало с максимумом функции, наименьшее значение совпало с минимумом функции.  У_наиб (Х₂)  и У_наим (Х₃)  .

Рис.2. На отрезок [a;b] попадают три  критические точки (Х_1, Х₂ и Х₃). Наибольшее значение получилось на конце промежутка в т. а : У_наиб (а) , наименьшее – в критической точке  Х₃ :

У_наим (Х₃) .

Рис.3.  На отрезок [a;b] попадают две  критические точки (Х₁ и Х₂). В данном случае наибольшее значение совпало с максимумом функции в точке Х_{2 ::} У_наиб (Х₂),  наименьшее значение получилось на конце промежутка в т. b : У_наим (b).

Рис.4.  На отрезок [a;b] попадают две  критические точки (Х₁ и Х₂). Наибольшее и наименьшее значение оказываются на концах отрезка:   У_наиб (b),  У_наим (а).

        Алгоритм нахождения наибольшего и наименьшего значения функции  y = f(x) на отрезке [a;b]

1.       Найти производную f  ´(x).

2.       Найти стационарные и критические точки  (приравнять производную к нулю, то есть

найти  f  ´(x)=0).

3.        Из полученных точек выбрать те, которые попадают в заданный  по  условию отрезок.

4.       Вычислить значение функции в выбранных точках и на концах промежутка.

5.        Из полученных чисел выбрать самое наибольшее У_наиб и самое наименьшее У_наим.

Рассмотрим примеры на данную тему.

Пример 1.  Найти наибольшее и наименьшее значение функции   f(x)= х⁴ - 2x² – 3   на отрезке  [ 0; 2]. В ответ записать наименьшее значение.

Решение.

1.Найти производную f  ´(x).

f ´ (x)= (х⁴ - 2x² – 3 )´ = 4 х³ - 4 х

2. Найти  f  ´(x)=0.

4 х³ - 4 х =0      4х ( х² – 1 )= 0    4 х= 0    х² – 1 =0     х = 0,  х= 1,  х= - 1

3.  Из полученных точек   х = 0,  х= 1,  х= - 1  выбрать те, которые попадают в заданный отрезок [ 0; 2].

0 ϵ [ 0; 2],       1 ϵ [ 0; 2],        - 1 не  ϵ [ 0; 2].

4. Вычислим значение заданной функции в выбранных точках    х = 0,  х= 1 и на концах отрезка[ 0; 2].

f(0)= 0⁴ – 2 · 0² – 3 = - 3

f(1)= 1⁴ – 2 ·1² – 3  = -4

f(2)= 2⁴ – 2 ·2² – 3  = 5

f наиб (2)  =5      f наим (1)  = - 4                  Ответ:         - 4

Пример 2.  Найти наибольшее и наименьшее значение функции   f(x)= х³/ 3 - x² /2 – 2х +10   на отрезке  [ -3; 3]. В ответ записать наибольшее значение. (Ответ округлить до десятых).     

Решение.

1.       f ´(x)= (х³/ 3 - x² /2 – 2х +10 )´ = х² – х -2

2.      х² – х -2 = 0     D = ( -1)² – 4 ·1· (- 2) = 1 +8 =9 = 3²

X₁ = ( 1+√9) / 2 = (1+3) / 2 =2           X₂ = ( 1- √9) / 2 = (1-3) / 2 = - 2 / 2  = - 1

3.       2 ϵ [ -3; 3],      - 1 ϵ [ - 3; 3].

4.          f(2)= 2³ / 3 - 2² /2 – 2 ·2 +10  = 8 / 3 -2 - 4 +10 = 6,7

 f(- 1)= (-1)³/ 3 – (-1)² /2 – 2·(- 1) +10  = (-1) / 3 – 1 / 2 +2 + 10 = 11,17

f(-3)= (-3)³/ 3 – (-3)² /2 – 2(-3) +10  = - 9 -4,5 + 6+ 10 =2,5

f(3)= 3³/ 3 - 3² /2 – 2·3 +10  =   9 - 4,5 – 6 + 10 = 8,5

f наиб (2)  =11,17        f наим (1)  = 2,5             Ответ:   11,2    

Пример 3.  Найти наибольшее и наименьшее значение функции   f(x)= 9 Cos x + 16x - 8   на отрезке  [ -3π/2; 0]. В ответ записать наибольшее значение.  

  Решение.

1.      f´ (x)= (9 Cos x + 16x - 8 )´  = - 9 Sinx +16

2.     - 9 Sinx +16 =0      - 9 Sinx =- 16      Sinx = ( - 16) / (- 9)= 1,8  > 1 – нет решения, так как     - 1 < Sinx  < 1.  Критических точек нет. Сразу выполняем пункт 4.

3.     Найдем значение функции на концах промежутка.

f(-3π/2)= 9 Cos (-3π/2 )+ 16 ·( -3π/2) - 8 = 9Cos (π/2) - 24π -8 =

9 ·0 - 24·3,14 – 8= - 83,36

f( 0)= 9 Cos (0 )+ 16 ·( 0) - 8 = 9·1 + 0 – 8 =1

f наиб (0)  =1        f наим (-3π/2)  = - 83,36            Ответ:   1

Пример 4.  Найти наибольшее и наименьшее значение функции   f(x)= 12 tg x – 12x+ 3π - 13   на отрезке  [ -π/4; π/4]. В ответ записать наибольшее значение.

Решение.

1.      f ´(x)= (12 tg x – 12x+ 3π – 13)´  = 12 / Cos² x – 12 + 0 – 0

(Примечание: производная ( 3π)´ = 0 так как это постоянная величина)

2.      12 / Cos² x – 12 =0  12(1 / Cos² x – 1)=0         1 / Cos² x =1      

 Cos² x =1       Cos  x =1  и  Cos  x = - 1. Получили два  простейших тригонометрических уравнения, для которых используем формулы частных случаев.

Cos  x =1         х = 2πn,  n ϵ Z.   При  n = 0      х = 2π·0 =0

 Cos  x = - 1    х = π + 2πn,  n ϵ Z.   При  n = 0      х = π + 2π·0 = π

3.      0 ϵ[ -π/4; π/4] ,         π  не ϵ [ -π/4; π/4] .

4.       f(0)= 12 tg 0 – 12·0+ 3π - 13  =12·0 - 12·0 +3·3,14 -13= -3,6

f(-π/4)= 12 tg (-π/4) – 12·(-π/4) +3π - 13 =12·( -1) + 3π +3π – 13=

-12 +6π -13 = -25 +6π = -25 +18,84 = - 6,16

f(π/4)= 12 tg (π/4) – 12·(π/4) +3π - 13 =12·( 1) - 3π +3π – 13= - 1

f наиб (π/4)  = -1        f наим (-π/4)  = - 6,16           Ответ:         - 1

Решить самостоятельно.

1.    Найти наибольшее и наименьшее значение функции  

 f(x)= х³ +4x² – 3х - 12   на отрезке  [ - 4; - 1]. В ответ записать наибольшее значение.

2.    Найти наибольшее и наименьшее значение функции  

 f(x)= х³ - 20x²  + 100х + 23   на отрезке  [  9;  13]. В ответ записать наименьшее значение.

3.    Найти наибольшее и наименьшее значение функции   

f(x)= 27х-  13 Sinx +11   на отрезке  [ -2π ; 0]. В ответ записать наибольшее значение.

4.       Найти наибольшее и наименьшее значение функции

  f(x)= 15 tg x – 15x+ 4   на отрезке  [ 0; π/4]. В ответ записать наименьшее значение.

Ответы.

1.    f _наим ( - 1)  = -6     f _наиб ( - 3)  = 6                 6

2.     f _наим ( 10)  = 23     f _наиб ( 13)  = 140           23   

3.     f _наим ( -2π) =- 158,56     f _наиб ( 0)  = 11      11   

4.    f _наим ( 0)  = 4       f _наиб (π/4 )  = 7,2               4