
Приведение
подобных радикалов
и применение формул сокращённого умножения
при преобразовании выражений с корнями
Цель: формировать умения выделять и приводить подобные радикалы, преобразовывать выражения, содержащие корни, с использованием формул сокращённого умножения.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
1. Вынесите множитель из-под знака корня:
а) ![]() ; б)
; б)
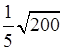 ; в)
; в)
![]() .
.
2. Внесите множитель под знак корня:
а) 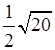 ; б)
; б)
![]() ; в)
; в)
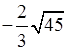 .
.
3. Сравните значения выражений:
а) ![]() и
и ![]() ; б)
; б)
![]() и
и 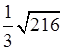 .
.
В а р и а н т 2
1. Вынесите множитель из-под знака корня:
а) ![]() ; б)
; б)
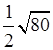 ; в)
; в)
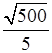 .
.
2. Внесите множитель под знак корня:
а) ![]() ; б)
; б)
![]() ; в)
; в)
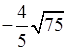 .
.
3. Сравните значения выражений:
а) ![]() и
и ![]() ; б)
; б)
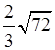 и
и ![]() .
.
III. Объяснение нового материала.
Сначала необходимо, чтобы учащиеся вспомнили все свойства квадратных корней и все виды преобразований выражений с корнями, которые они уже умеют выполнять.
Затем рассмотреть несколько примеров, отражающих другие виды преобразований: приведение подобных радикалов и применение формул сокращённого умножения.
П р и м е р 1 (пример из учебника).
П р и м е р 2. Преобразуйте выражение:
а) ![]() = 20
– 9 = 11;
= 20
– 9 = 11;
б) ![]() = 7.
= 7.
Остальные виды преобразований целесообразно рассмотреть на следующем уроке.
IV. Формирование умений и навыков.
Учащимся уже известно понятие «подобные слагаемые».
На этом уроке вводится понятие «подобные радикалы» и формируется умение упрощать соответствующие выражения.
З а д а н и я, которые должны быть выполнены на этом уроке, можно разбить на д в е г р у п п ы:
1) Выделение и приведение подобных радикалов.
2) Преобразование выражений, содержащих корни, с использованием формул сокращенного умножения.
1-я г р у п п а.
1. Приведите подобные слагаемые.
а) ![]() ; в)
; в)
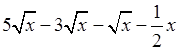 ;
;
б) ![]() ; г)
; г)
![]() .
.
2. № 421, № 422 (а, в).
2-я г р у п п а.
1. № 423, № 426.
2. № 425.
Р е ш е н и е
а) ![]()
![]()
= 8 + 6 = 14.
б) ![]()
![]() = 8.
= 8.
Сильным в учебе учащимся можно предложить дополнительно выполнить задания по карточкам.
К а р т о ч к а № 1
1. Упростите выражение:
а) ![]() ;
;
б) ![]() ;
;
в) 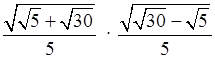 .
.
2. Докажите, что ![]() = 2.
= 2.
3. Выберите выражение, равное ![]() :
:
А. ![]() – 3; Б.
– 3; Б.
![]() ; В.
3 –
; В.
3 – ![]() .
.
К а р т о ч к а № 2
1. Упростите выражение:
а) ![]() ;
;
б) ![]() ;
;
в) 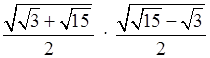 .
.
2. Докажите, что ![]() = 33.
= 33.
3. Выберите выражение, равное ![]() :
:
А. ![]() – 2; Б.
– 2; Б.
![]() ; В.
; В.
![]() .
.
Р е ш е н и е з а д а н и й карточки № 1
1. а) ![]()
![]() ;
;
б) ![]() ;
;
в) 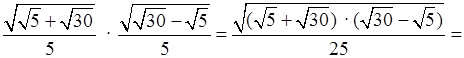
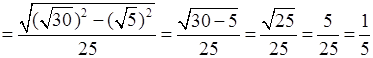 .
.
2. ![]()
![]()
![]()
![]() = 2.
= 2.
3. Выражение А является отрицательным, поэтому его можно не проверять. Возведём выражения Б и В в квадрат.
![]() ;
;
![]() .
.
О т в е т: В.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие существуют виды преобразований квадратных корней?
– Как привести подобные радикалы?
–
Рациональным или иррациональным является выражение вида ![]() ?
?
Домашнее задание: № 422 (б, г, д, е), № 424.
Д о п о л н и т е л ь н о: № 496.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.