Проект п теме "Математика вокруг нас"

 

ГКОУ

«Кочубейская средняя общеобразовательная

 школа- интернат»

 

 

                                 Исследовательский проект.

 

 

Математика вокруг нас !

 

 

 

 

Авторы:

 учащиеся  6 «а» класса                                                  

                                                          Руководитель:

                                                                        Лисицкая Ольга Николаевна                                  

                                                     учитель  математики.

                                                                                           

     2020 год

 

 

 

 

Оглавление

 

                                                                                                                      стр.

1.     Введение (цель, задачи, гипотеза, методы исследования)            2                     

2.     История возникновения математики                                               3

3.     Применение математики                                                                  10

3.1.         Математика в быту.

3.2.         Математика в профессиях

3.3.         Математика  и архитектура.

3.4.         Математика и живопись.

3.5.         Математика  в жизни животных.

3.6.          Математика в природе.

3.7.         Математика в  маркетинге.

4.     Практическая  часть.                                                                         22

5.     Заключение                                                                                        23

6.     Список используемых источников и литературы                          24

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

 

Цель исследовательской работы:

1.     Изучить значение математики в жизни человека.

2.     Доказать необходимость знаний основ математики в повседневной жизни.

3.     Повысить интерес обучающихся к изучению математики.

Задачи исследовательской работы:

1.       Выяснить историю возникновения математики, где и когда зародилась математика, счет у некоторых народностей.

2.       Ответить на вопросы: зачем нам нужна математика? что может дать математика каждому из нас?  Как часто  приходится взрослым решать в повседневной жизни математические задачи? Где и как используются  математические знания в повседневной жизни.

3.       Рассмотреть и проанализировать взаимосвязь между математикой и жизнью.

4.       Развить навык  работы с дополнительной литературой;   развить        умения анализировать и систематизировать полученные данные; развить умения обобщать, делать выводы и заключения.

5.       Создание буклета «Математика вокруг нас».

  Тип работы: исследовательский,  внутри классный, краткосрочный.

 

Гипотеза: если в повседневной жизни можно обойтись  без знаний математики, то    все, что мы изучаем на уроках математики нам в дальнейшем, не пригодится.

 

Практическая значимость: если гипотеза подтверждается, следовательно, можно утверждать, что без  знаний математики можно обойтись; если нет, то без знаний математики вся современная жизнь была бы невозможна.

 

Методы исследования:

·        изучение литературы по данной теме, её анализ;

·        сбор общественного мнения, наблюдение.

Класс разбит на четыре группы:

I группа  «Историки».

Руководитель группы: Арсланукаева У, Магомедов М.

Задачи группы: Выяснить где и когда зародилась математика, рассмотреть историю возникновения счета.

II группа «Теоретики».

Руководитель группы: Хабибулаева Д,  Дибирасулаева Х.

Задачи группы: Ответить на вопросы: зачем мы изучаем математику? что может дать математика нам?  Где и как используются  математические знания в повседневной жизни.

III группа «Практики».

Руководитель группы: ,  Дибирасулаев Шамиль

Задачи группы: Рассмотреть и проанализировать взаимосвязь между математикой и жизнью. Как часто  приходится взрослым решать в повседневной жизни математические задачи?

IVгруппа «Социологи».

Руководитель группы: Абакаров М,  Алиева С.

Задачи группы: провести опрос среди работников школы и родителей своего класса с целью выяснить используют ли они полученные в школе знания по математики в своей профессии, в быту.

 

Тот, кто не знает математики,

не может узнать никакой другой

науки и даже не может обнаружить своего невежества

Роджер Бэкон, XII в.

 

2. История возникновения  арифметики и геометрии

    

   Мы знаем, что математика берет свои корни из глубокой древности, и возникла она из практической потребности людей. У каждого народа необходимость в простейших арифметических подсчетах возникала задолго до появления первых зачатков письменности, потому что постижение Мира во всем его многообразии постоянно требовало количественной оценки обретенных знаний. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног, делали зарубки, завязывали узелки.

Учёные - археологи обнаружили стойбище древних людей. В нём они нашли волчью кость, на которой  30 тысяч лет назад какой - то древний охотник нанёс 55 зарубок. Видно, что, делая эти зарубки, он считал по пальцам.

Много тысячелетий прошло с тех пор. До сих пор в русском языке сохранилось слово «бирка». Теперь так называют дощечку с номером, которой отмечают товар. А ещё 200 - 300 лет тому назад так называли куски дерева, на которых зарубками отмечали сумму долга. Бирку с зарубками раскалывали пополам. При расчёте половинки складывались вместе, и это позволяло определить сумму долга без споров и сложных вычислений.

Первыми понятиями математики, с которыми столкнулись люди, были «меньше», «больше», «столько же». Если одно племя меняло рыбу на сделанные другим племенем каменные ножи, достаточно было положить рядом с каждой рыбой один нож, чтобы сделка состоялась.

А вот так выглядело счётное устройство инков.

 

 

 

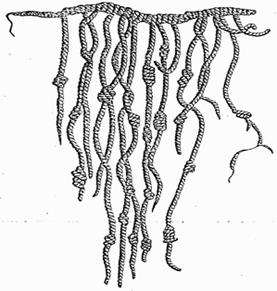
Для запоминания результатов счёта использовали зарубки, узелки и так далее.

Одна из древнейших нумераций, дошедших до нас в древних папирусах и рисунках – египетская.

Египтяне придумали эту систему около 5 000 лет тому назад. Это одна из древнейших систем записи чисел, известная человеку. Для записи чисел египтяне использовали картинки иероглифы, означавшие:

     Все остальные чис­ла составлялись из основных чисел, которые приведены в таблице, с помощью сложения. При записи числа иероглифы единицы, десятка, сотни и т. д. писались столько раз, сколько в этом числе единиц соответствующего разряда. Разряды писались справа налево (слева – меньшие, справа – большие) – в обратном порядке, чем у нас сейчас.

    Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.

Рассмотрим примеры записи некоторых чисел: 

     

 - 3000030.

      Далее постепенно у разных народов и племен стали появляться названия для чисел. Недаром ведь говорят: «Без названия, нет знания».  Учёные считают, что сначала названия получили числа 1 и 2.

Когда римляне придумали имя числу 1- «солюс»,  они исходили из того, что Солнце на небе одно. А название для числа 2 во многих языках связано с предметами, встречающимися попарно, - крыльями, ушами.

А на языке некоторых папуасских племён число 1 называлось  «урапун», число 2 - «оказа», а названия для остальных чисел строилось исходя  из состава числа, например:

3 (2+1)  - «оказа -урапун»,

4 (2+2)  - «оказа - оказа»,

        5 (2+2+1) - «оказа - оказа - урапун»,

        7 (2+2+ 2 +1) - «оказа - оказа – оказа - урапун»,

        8 (2+2+2+2) - «оказа – оказа - оказа - оказа» и т. д.

Как писать, так и считать тогда умели только специально обученные люди, для простых людей счет был так же недоступен, как и письменность. Эта система применялась в Древнем Египте при торговле и сборе податей, особенно распространившись при постройке Великих Пирамид, и постепенно угасла вместе с кастой строителей и счетоводов, при упадке Египта и подчинении его власти Александра Македонского.

Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумать названия для чисел.

 

Античная математика.

Третий век до нашей эры был золотым веком античной математики.

В 389 году до н. э. Платон основывает в Афинах свою школу - знаменитую Академию.

В III веке до н. э. в городе Александрия Птолемей I основал Дом Муз и пригласил туда виднейших учёных. Это  была первая академии, с богатейшей библиотекой, которая к I веку до н. э. насчитывала 70000 томов.

Но самая громкая слава выпала на долю трёх великих геометров древности - Евклид (написал книгу «Начала», авторитет которой был огромным в течение 2000 лет),  Архимед (развил метод вычисления площадей и объёмов фигур) а  Аполлоний Пергский (провел огромные  исследования сечений). 

Два достижения греческой математики далеко пережили своих творцов.

1.     греки построили математику как целостную науку;

2.     греки провозгласили, что законы природы постижимы для человеческого разума.

 

 

Страны ислама

 

Математика Востока, в отличие от греческой, всегда носила более практический характер. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия, механика, оптика.

Восточная математика возникала как прикладная наука, имевшая целью облегчить календарные расчеты, распределение урожая, организацию общественных работ и сбор налогов. Вначале, естественно, главным делом были арифметические расчеты и измерения. Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века, изображает число 35 в виде серии выстроенных в ряд 35 палочек-пальцев. Первыми существенными успехами в арифметике стали концептуализация числа и изобретение четырех основных действий: сложения, вычитания, умножения и деления. Однако в науке, которую столетиями культивировали специалисты, чьей задачей было не только ее применение, но и посвящение в ее тайны, должен был развиться абстрактный уклон. Постепенно наукой стали заниматься ради нее самой. Из арифметики выросла алгебра не только потому, что это облегчало практические расчеты, но и в результате естественного развития науки, культивируемой и совершенствуемой в школах писцов. В силу тех же причин из измерений возникли начатки (но не больше) теоретической геометрии. Обе развивающиеся науки стали использоваться в решении задач, поставленных торговлей, архитектурой, астрономией, географией, оптикой.

Математика у русского народа

Письменные памятники математических знаний русского народа мы можем наблюдать, начиная примерно с тысячного года нашего летосчисления. Эти знания являются результатом предшествовавшего долгого развития и основаны на практических нуждах человека.

Бирки - расчетные палочки

Рано возник в России интерес к науке в широких слоях населения. Сохранились сведения о школах при Владимире Святославовиче (978-1015), при Ярославе Мудром (1036-1054). Находились в очень раннюю эпоху "числолюбцы", интересовавшиеся математикой не только в той мере, в какой она были нужна непосредственно для практической деятельности.

Примером таких "числолюбцев" был новгородский монах начала двенадцатого столетия Кирик.

Говоря об интересе русского народа к математике в те отдаленные от нашего времени века, мы не должны забывать, что речь здесь идет о передовых слоях народа, стремившихся к знанию, строивших национальную культуру, которая пышно расцвела в последующие века.

Рядом с этими прогрессивными элементами имелись значительные круги духовенства и эксплуататоров, которые относились к знанию вообще и к математике в частности враждебно. Свидетельства о враждебном отношении к знанию мы встречаем еще в XVII и XVIII веках.

Основной предпосылкой для всех математических знаний служит нумерация, которая у разных древних народов имела различный вид.

По-видимому, все народы вначале обозначали числа зарубками на палочках, которые у русских назывались бирками. Такой способ записей долговых обязательств или налогов употреблялся малограмотным населением разных стран. На палочке делали нарезы, соответствующие сумме долга или налога.

Палочку раскалывали пополам; одну половину оставляли у должника или у плательщика, другую хранили у заимодавца или в казначействе.

При расплате обе половинки проверяли складыванием. В Англии этот способ записей налогов существовал до конца семнадцатого столетия. При ликвидации старых налоговых обязательств крестьян на дворе лондонского казначейства был устроен костер из накопившихся бирок. Этот костер оказался таким большим, что сгорело и само здание казначейства, а вместе с ним погиб и вделанный в стену образец английской меры длины, так что с тех пор англичане не знают точной длины своего фута.

Греки в шестом столетии до нашего летосчисления стали обозначать числа буквами, снабженными особым значком. Таким же образом писали числа наши предки при помощи букв славянского алфавита, над которыми ставился особый значок - титло. Приведенная  ниже таблица показывает, какими буквами какое число обозначалось в славянской нумерации. Влиянием этой нумерации объясняются некоторые термины русского языка. В старых учебниках грамматики буква "и" называлась "и осьмиричное", буква "i" - "и десятеричное". Объясняются эти названия тем, что в славянской нумерации буква "и" обозначала 8, буква "i" - 10.

Славянская нумерация

Потребности хозяйственной жизни далекого прошлого довольствовались сравнительно небольшими числами - так называемым "малым счетом" наших предков. Он доходил до числа 10000, которое в самых старых памятниках называется "тьма", то есть темное число, которое нельзя ясно представить. Рассмотрим славянскую нумерацию для обозначения больших чисел

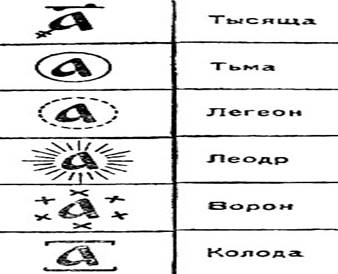
 В дальнейшем граница малого счета была отодвинута до 108, до числа "тьма тем". Старинная рукопись по этому случаю заявляет, что "больше сего числа несть человеческому уму разумети". Но наряду с этим "малым числом", "коли прилучался великий счет и перечень", употреблялась вторая система, называвшаяся "великим числом или счетом" или "числом великим словенским". В нем употреблялись более высокие разряды: тьма - 10⁶, легеон - 10¹², леодр - 10²⁴, ворон - 10⁴⁸; иногда еще колода - десять воронов - 10⁴⁹ (хотя нужно было за колоду принять, следуя системе, 10⁹⁶). Для обозначения этих больших чисел наши предки употребляли оригинальный способ, не встречающийся ни у одного из известных нам народов: число единиц любого из перечисленных высших разрядов обозначалось той же буквой, что и простые единицы, но обрамленной для каждого числа соответственным бордюром.

Таких больших чисел не требовала в то время, и не требует и теперь, ни одна из практических задач. Архимед, величайший греческий математик, сосчитал, что число песчинок во всем мировом пространстве, как это понимали в то время, не превышает 10⁶³. А славянский "числолюбец" сказал бы, что это число песчинок не больше "тысячи легеонов воронов" (10⁶⁸ = 10³ · 10¹²· 10⁴⁸). Число песчинок во всем мировом пространстве человеку того времени действительно могло казаться наибольшим мыслимым числом, чем и оправдываются заявления авторов рукописей о том, что "больше сего не дано человеку разумети".

Развитие науки в России в XIII веке было прервано нашествием монголов. После свержения ига оказалось, что Россия значительно отстала от других европейских стран. Огромную работу для преодоления этого отставания провел царь Пётр I.

Русский народ создал свою собственную систему мер длины с которой мы познакомились на уроках математики в 5 классе.

Древними русскими мерами длины, употреблявшимися уже в 11 – 12 веках были пядь, локоть, сажень.

Малая пядь равнялась расстоянию между концами вытянутых больших и указательных пальцев =19см, большая пядь - расстоянию между раздвинутыми большими и мизинцами =23см.

Локоть – расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба. Его длина колебалась от 38 см до 46 см или вершков. Её применяли в крестьянском хозяйстве, когда нужно было измерить длину изготовленной в домашних условиях шерстяной пряжи или пеньковой верёвки (такую продукцию наматывали на локоть).

Сажень - расстояние от ступни до конца среднего пальца поднятой руки = 3 аршинам = 7 футам ( 2,13 м)

С развитием производства и торговли люди убедились в том, что не всегда удобно измерять расстояние шагами или прикладыванием локтя. Кроме того, такое измерение уже не удовлетворяло возросшим требованиям точности. В самом деле, длина локтя или шага у разных людей различна, а мера длины должна быть постоянной. Постоянные образцы мер стали изготовлять из деревянных линеек и металлических стержней. Образцы мер в настоящее время называются эталонами.

Старой русской мерой длины был аршин, который делился на 16 вершков и  равен 28 дюймам ( 71,12 см). Когда говорили о росте человека, то указывали лишь, на сколько вершков он превышает 2 аршина. Поэтому слова «человек 12 вершков роста» означали, что его рост равен 2 аршинам 12 вершкам, то есть 196 см. Миля = 7 верстам ( 7,47 км), верста = 500 саженям ( 1,07 км), фут = 12 дюймам (30,48 см), дюйм = 10 линиям ( 2,54 см) и 1 линия = 10 точкам ( 2,54 мм).

 

 

3.   Применение математики.

3.1. Математика в быту.

    Жизнь наших родителей непосредственно связана с математическими расчетами. Наши мамы и бабушки ежедневно ведут семейный бюджет: на оплату коммунальных услуг, на питание, на покупку одежды, транспортные расходы, на медицинское обслуживание, на ремонт квартиры,  на отдых и т.д.

Рассмотрим задачи, которые приходится решать ежедневно нашим родителям.

1.                 Каждый день мы готовим пищу. Мама и бабушка большинство рецептов помнят наизусть и готовят, как они говорят, «на глаз». Но когда они приступают к приготовлению пищи, то выясняется, что без математики не как не обойтись.

Задача 1.  Для приготовления салата из шампиньонов на 4 порции необходимо взять по ½ желтого, зеленого и красного сладкого перца, 150 грамм шампиньонов, 100 грамм сыра, 4 ст. ложки майонеза, зелень укропа, 1 чайная ложка сока лимона, 25 грамм сливочного масла для жарки. А если этот салат необходимо приготовить на 8 порций, то все продукты необходимо увеличить, т.е. умножить на 2 и т.д.

Задача 2.  Для приготовления клубничного варенья на зиму бабушка  берет 1 часть сахарного песка и 2 части ягод клубники. Если собрано 7 кг ягод клубники, то опять необходимы математические расчеты что бы определить сколько надо взять сахарного песка:

	часть	масса, кг.
Сахар	1	х
Ягода	2	7

Составим пропорцию и получим, что на 7 килограмм  ягод клубники необходимо бабушке взять 3,5 кг сахарного песка.

Задача 3. Для при­го­тов­ле­ния фарша взяли го­вя­ди­ну и сви­ни­ну в от­но­ше­нии 7:13. Какой про­цент в фарше со­став­ля­ет сви­ни­на?

Ре­ше­ние.

Пусть вязли 7х г го­вя­ди­ны, тогда сви­ни­ны взяли 13х г. Сле­до­ва­тель­но, сви­ни­на со­став­ля­ет в фарше А если нам будет известно, что мама приготовила 630  грамм мяса говядины, то мы не нарушая пропорций рецепта возьмем нужное количество, необходимо взять (630: 7· 13) 1килограмм 170 грамм мяса свинины.

2.                 Ежедневно приходится нам совершать покупки в магазинах, производить математические расчеты.   С целью экономии семейного бюджета,  приходится вести наблюдение за ценами в разных магазинах и прибегнув к математическим расчетам выбрать наиболее дешевый набор продуктов. Очень часто в витринах магазинов мы наблюдаем предпраздничные скидки, и здесь нам ни как не обойтись без математических знаний - понятия «пропорция», «отношения», «процент».

Задача  1.  Чашка, ко­то­рая сто­и­ла 90 руб­лей, продаётся с 10%-й скид­кой. При по­куп­ке 6 таких чашек мама отдала кас­си­ру 1000 руб­лей. Сколь­ко руб­лей сдачи она дол­жна по­лу­чить?

        Решение:

Сто­и­мость одной чашки равна 90 − 0,1 · 90 = 81 руб. Сто­и­мость 6 таких  чашек равна 486 руб. Зна­чит, сдача с 1000 руб­лей со­ста­вит 514 руб­лей.

Задача 2. В  таблице  указаны  средние  цены  (в  рублях)  на  некоторые  основные  продукты  питания в трех магазинов г. Волгодонска.

Наименование продукта	«Магнит»	«Артемида»	Магазин № 24
Пшеничный хлеб	21	21,5	22
Молоко (1 литр)	37	45	58
Картофель (1 кг)	23	20	22
Подсолнечное масло (1 литр)	58	64	71
Мясо (говядина)	260	280	300

 

Необходимо определить,  в  каком  из  этих  трех магазинов  окажется  самым  дешевым  следующий  набор продуктов для  семьи: 2  батона  пшеничного  хлеба, 3  кг  картофеля, 1,5 кг  говядины, 1  л  подсолнечного масла. 

«Магнит», стоимость необходимого  набора продуктов составила: 559 рублей.

«Артемида», стоимость необходимого  набора продуктов составила: 587 рублей.

Магазин №24, стоимость необходимого  набора продуктов составила: 631 рублей.

  Для покупки продуктов мы выберем магазин «Магнит», где наша экономия составит от 28 рублей до 72 рублей.

3.                 Ежемесячно нам,  приходят квитанции по  оплате  коммунальных платежей (за квартиру, телефон,   электричество, газ и воду и т.д.). Чтобы оплатить коммунальные услуги,  например, за потребление газа  необходимо произвести математические расчеты  найти разность между текущими показаниями счетчика и учтенными. Количество потребленного газа умножим на стоимость 1 м³.

Задача 1. Предыдущие показания газового счетчика на начало февраля показало 1020 м², текущие показания на конец  месяца составило 1372 м² , значит   потребление газа за февраль составило 352 м².  И  так за февраль необходимо произвести оплату за потребления газа (352м² ·5,66557 рублей, после округления) 1994,28 рублей.

4.          А сколько же приходится выполнить математических вычислений и расчетов, во время  ремонта квартиры? Мы удивляемся своим родителям, какой это труд, чтобы составить мини план и сделать расчёт количества необходимых материалов (определить нужное количество  обоев, клея, ламината,  сколько уйдёт штукатурной смеси и т.д.), а также учесть свой бюджет. Для всех этих расчетов необходимы   знания математические полученные  в школе, это: нахождение площади комнат и стен, периметра и т.д. От этих точностей  будет зависеть  качество ремонта, а также расходы на транспортное средство по доставке и  хватит ли нам  материалов:  штукатурной смеси, обоев, чтобы отштукатурить и оклеить стены комнат.

Рассмотрим некоторые  расчеты, для ремонта детской комнаты,  подберем  необходимое количество  строительных материалов и   посчитаем, сколько для этого необходимо  денег.

Задача 1. Площадь  комнаты 12 м² , длина=4м., ширина 3м. а высота 2,5м.

Потолок 12 м²: 

- натяжной потолок, стоимость 1м² – 220 рублей, итого 2640 рублей;

- точечные светильники 6 штук по 148 рублей, итого 888 рублей;

- электрический провод 11 метров по 17 рублей, итого 187 рублей.

Пол 12 м² :

- Ламинат «Дуб серый», 385 рублей за 1м², итого 4620 рублей;

- Подложка под ламинат, 12м² по 27 рублей, итого 324 рубля;

- Плинтуса 14 метров, 2,5 метра – 145 рублей, надо купить 6 штук, итого 870 рублей;

Стены 35 м² – 3,7 м² = 31,3м² (отняли площадь окна и двери):

- Шпаклевка 2 мешка по 270 рублей, итого 540 рублей;

- Обои.  Казалось бы, что может быть проще расчета  количества обоев? На рулонах написана площадь обоев (10м² при ширине 1,06м). Но нужно учесть подгонку по рисунку (рапорт) и припуск на подрезку. Из рулона 10 метров, всегда выходит только 3 полосы. Мы выбрали обои с подгонкой по рисунку, после математических подсчетов необходимо 5 рулонов по 1,400 рублей, итого 7000 рублей;

- Клей для обоев 1 пачка за 275 рублей.

Все запланированные работы по ремонту, мы будем выполнять  своими силами, чтобы сэкономить денежные средства,  так как строители за работу берут довольно не маленькие деньги. После проведенных подсчетов получаем, что ремонт детской комнаты 12 м² , нам обойдется в 17344 рубля.

5.           Когда возникают проблемы со здоровьем, у нас и наших родных, мы обращаемся в медицинские учреждения, и лечащий врач выписывает рецепт, в котором назначает курс лечения. Где нам необходимо опять же выполнить некоторые математические расчеты.

    Задача 1 . Врач прописал больному курс лекарства, которое нужно пить по 0,5г.  три раза в день в течение двух недель. В одной упаковке содержится 10 таблеток по 0,5г. Какого наименьшего количества упаковок хватит на весь курс лечения?

        Решение:

1) 0,5·3·14=21(г) - лекарства нужно для лечения в течение 14 дней.

2) 10·0,5=5(г)  - масса 1 упаковки. 

 3)21:5=4,2 (упаковок лекарства). Значит, для прохождения всего курса лечения нам необходимо купить 5 упаковок лекарства.  

 

3.2.        Математика в профессиях.

Существует ряд профессий, которым математика нужна в «чистом» виде. Это экономист, инженер, предприниматель, бизнесмен, программист и т.д. Им необходимо умение вычислять, пользоваться различными формулами и т.д. А есть ряд профессий, которым, на первый взгляд, математика совсем не нужна. Например, массажист, токарь, футболист, следователь, юрист, адвокат, ветеринар т.д. Но в ходе исследования мы убедилась, что математику просто обязательно надо изучать

Задача №1.(для строителя).

Вычислите площадь стен дома снаружи. Высота дома 3м. Размер дома 12х11м. Сколько нужно облицовочного кирпича, если для того, чтобы выложить 1м² требуется 52 кирпича?

В одном поддоне 400 штук кирпича. Сколько стоит кирпич, если один поддон стоит 4200 рублей?

 

 

Задача №2 (для строителя).

При строительстве сельского дома можно использовать один из двух типов вариантов фундамента: каменный или бетонный. Для каменного фундамента необходимо 9 тонн природного камня и 9 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1600 рублей, щебень стоит 780 рублей за тонну, а мешок цемента стоит 230 рублей. Сколько рублей придется заплатить за материал для фундамента, если выбрать самый дешевый вариант?

Задача №3. (для юриста).

У трех подружек - Кати, Насти и Олеси - новогодние карнавальные костюмы белого, синего и фиолетового цветов, и шапочки тех же цветов. У Насти цвет костюма и шапочки совпали, у Кати ни костюм, ни шапочка не были фиолетового цвета, а Олеси была в белой шапочке, но цвет костюма у нее не был белым. Как были одеты девочки?

Задача №4 (для врача).

Больной должен принимать лекарство по 1 мг в порошках 4 раза в день в течении 7 дней, то сколько необходимо выписать данного лекарства ( расчет вести в граммах).

Задача №5 (для повара).

Определить, сколько килограммов сухарей с влажностью 15% можно получить из 255 кг хлеба с влажностью 45%.

Задача 6 (для дворника).

В бригаде 5 дворников. Площадку для праздника они могут расчистить за 210 минут. Но праздник начинается раньше. Сколько помощников им надо взять, чтобы расчистить площадку за 150 минут?

Задача №7 (для парикмахера).

 Имеется два раствора перекиси водорода: 30-процентный и 3-процентный. Нужно их смешать так, чтобы получился 12-процентный раствор. 

Задача №8 (для предпринимателя).

Предприниматель купил акции и через год продал их, получив прибыль, причем полученная сумма составила 11500р. Сколько акций было куплено, если прибыль от стоимости каждой акции составила 150р  и равна 15%?

 

3.3.          Математика и архитектура.

       Математика – это не только точная наука и  определенная система законов, но и уникальное средство познания красоты. А красота многогранна и многолика.

    На уроках математики мы знакомимся с понятием «пропорция».  Что же такое пропорция? Пропорция - равенство двух отношений: a : b = c : d.

   Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему:

   a : b = b : c или с : b = b : а.  

Рассмотрим где можно увидеть золотое сечение – гармоническую пропорцию.

 

 Одним из красивейших произведений  древнегреческой архитектуры является Парфенон (V в. до н. э.).

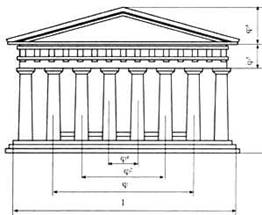
Фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза. Парфенон имеет 8 колонн по коротким сторонам прямоугольника и 17 по длинным. Отношение высоты здания к его длине равно 0,618.

Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери, и в пирамиде Хеопса, и в храме Василия Блаженного на Красной площади.

 

            

 

       «Золотое сечение» можно обнаружить в прекрасном творении    В. Баженова, которое прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г.

 

 

 

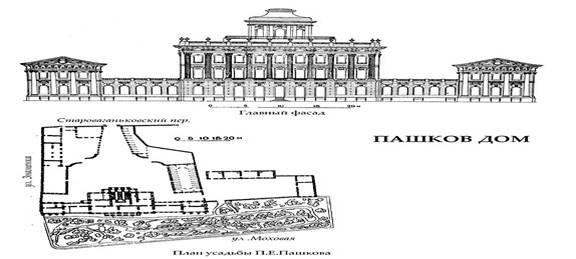
      Золотая пропорция  применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображённого человека делится пупочной линией в золотом сечении (талия делит совершенное человеческое тело в отношении золотого сечения  примерно  )

 

 

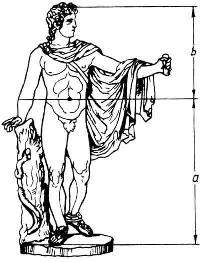
Скульпторы утверждают, что пропорции мужчин ближе к золотому сечению, чем пропорции женщин (однако, женщина в обуви на каблуках может оказаться ближе к золотым пропорциям).

3.4.          Математика и  живопись.

Во все эпохи процветания искусство вступало в союз с наукой. Художники-мыслители, теоретики и педагоги, размышлявшие над проблемами обучения молодых, всегда приходили к выводу, что без науки искусство развиваться и процветать не может. Художник и педагог Н. П. Крымов писал: «Говорят: искусство не наука, не математика, что это творчество, настроение и что в искусстве ничего нельзя объяснить — глядите и любуйтесь. По-моему, это не так. Искусство объяснимо и очень логично, о нем нужно и можно знать, оно математично... Можно точно доказать, почему картина хороша и почему плоха». В. И. Суриков утверждал, что в композиции есть какой-то непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика.

Ещё в эпоху Возрождения художники открыли, что любая картина имеет определённые точки, невольно приковывающие внимание, так называемые зрительные центры. Таких точек всего 4, они делят величину изображения по горизонтали и вертикали в золотом сечении. Данное открытие у художников того времени получило название «Золотое сечение» картины.

Фигура А. С. Пушкина в картине Н. Н. Ге «Александр Сергеевич Пушкин в селе Михайловском» поставлена художником на линии золотого сечения в левой части полотна (рис. 8). Но и все остальные величины по ширине вовсе не случайны: ширина печи равна 24 частям от ширины картины, этажерки — 14 частям, расстояние от этажерки до печи также равно 14 частям и т. д.

 

В ранней картине В. И. Сурикова «Милосердный самарянин» (1874) голова раненого помещена художником в правой нижней точке картины, ладонь правой руки самарянина — в левой верхней, где слуга льет в нее воду из кувшина. Обе эти точки находятся на диагонали. Устойчивость композиции придает и то, что голова самарянина находится на средней линии картины по вертикали:

Диагонали, линии золотого сечения и смысловой центр картины В. И. Сурикова «Милосердный самарянин»

 

Построение пейзажа по золотому сечению художник начинает разрабатывать эскиз пейзажа форматом 8x12 см. Для нахождения линии золотого сечения по вертикали и отрезков золотого сечения по нисходящему ряду можно воспользоваться проведением вспомогательной линии длиной 10 см за пределами поля эскиза.

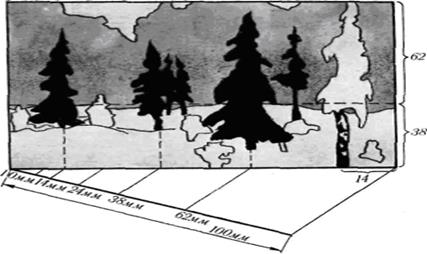
На этой замечательной картине И. И. Шишкина («Сосновая роща») так же просматриваются мотивы золотого сечения.

 

Наличие в картине вертикалей и горизонталей, делящих её в отношении золотого сечения, придаёт ей характер уравновешенности и спокойствия.

Рассматривая  примеры в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.

Портрет Моны Лизы привлекает тем, что композиция рисунка построена на «золотых треугольниках», являющихся частями правильного звездчатого пятиугольника. 
 

 

 

3.5.          Математика в жизни животных.

 «Математика и опыт – вот подлинные основания достоверного, естественного, разумного живого познания», Спиноза.

Мир животных - богатый и разнообразный мир живых существ. «Так причем здесь математика?» - скажите Вы. А мы вам скажем, что и здесь не обойтись без нее!                       

Пчелиные соты представляют собой пространственный паркет «шестигранные призмы», это математический шедевр из воска, созданный пчелами.

 

 

А если в лесу, в парке  обратить внимание на паутину, то мы увидим, что соблюдены строгие пропорции.

Строение живородящей ящерицы, то  с первого взгляда улавливаются приятные для нашего глаза пропорции. При общей длине ее тела 18 см  длина ее хвоста составляет 11 см, а остальная часть тела 7 см, при делении 11 на 7 получаем число 1,5714 которое близко к золотому числу (т.е. длина ее хвоста так относится к длине остального тела, как 62 к 38).

 

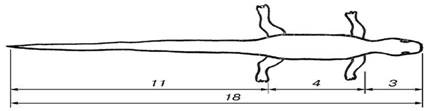
  У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и мы увидим тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

 

 

Большой интерес представляет исследование форм птичьих яиц.

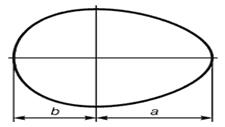 Линия проведенная по наиболее широкому месту яйца делит его на части «а» и «b» так, что часть «а» относится к части «b» в золотой пропорции.

3.6.          Математика в природе

«Природа формулирует свои законы языком математики»  Г.Галилей.

 

 

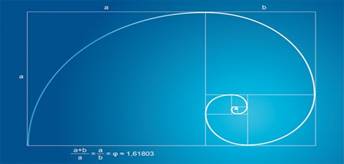
  Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.

  Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении семян подсолнечника, шишек сосны, ананасах, кактусах  и т.д. проявляет себя ряд Фибоначчи, то есть, проявляет себя закон золотого сечения.

 

 Среди придорожных трав растет ничем не примечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.

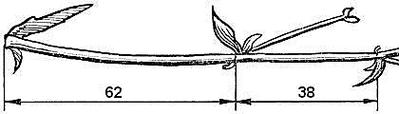 Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

3.7.        Математика в мерчандайзинге и маркетинге.

Всем известно, что любой владелец магазина стремиться получать максимальную прибыль. Как подтолкнуть покупателя к большему количеству покупок, или «заставить» купить товар, который ему не нужен был до входа в магазин? Именно в этих целях в мерчандайзинге и маркетинге применяется множество способов, одним из которых является правило золотого треугольника.

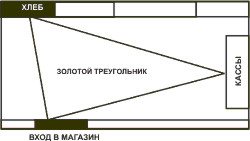
Правило золотого треугольника в мерчандайзинге гласит: основные точки, которые привлекают внимание покупателя - это вход, главная витрина (в ней зачастую размещают товары повседневного спроса) и касса. Чтобы охватить большую территорию полок и витрин с товарами импульсной покупки, расстояние между вершинами треугольника максимально увеличивают. Чем больше расстояние между вершинами золотого треугольника, тем больше покупатель затратит времени  на пребывание в магазине и, соответственно, тем больше товаров попадает в поле зрения потребителя, что подталкивает его в их покупке и повышает прибыль продаж магазина.

Исходя из этого принципа, строятся многие магазины (особенно магазины самообслуживания). Теперь давайте рассмотрим, как действует правило золотого треугольника в мерчандайзинге на конкретном примере.

   Самым классическим примером использования правила золотого треугольника служит обычный продуктовый сетевой магазин. Если задуматься, то за какой продукцией чаще всего мы приходим в магазин? Конечно же, это хлеб. Когда мы вспомним, где же обычно находится витрина с хлебом, то окажется что в самом отдаленном углу от зоны входа.

   Хлеб это товар, за которым специально каждый идет в магазин. Но, войдя в него, мы пройдем через весь торговый зал, обратив внимание на другие товары. И тут начинаем вспоминать, что же еще нужно было бы прикупить. К хлебу бы купить масла или джема, а там смотри, и чай дома заканчивается. А возле чая, посмотрев на цену сахара, подумываем, не купить ли и сахар. Таким образом, зайдя в магазин только за хлебом, к кассе мы направляемся уже с полной корзиной других продуктов, покупать которые мы и не собирались до входа в магазин.

 

 

4.     Практическая часть.

Прежде, чем сделать окончательный вывод, что для нас математика, мы предлагаем изучить результаты социологического опроса.

Цель опроса: изучение общественного мнения по данной теме.

Опрос вёлся  по следующим направлениям:

Для родителей:

1.     Используете ли Вы, математические знания, полученные Вами в школе:

- в своей профессии?

- в быту?

2. Считаете ли Вы, что без математических знаний нам в повседневной жизни не обойтись и «Математика – это жизнь»?

Для обучающихся:

1.         Зачем  надо изучать математику?

2.         Нужна ли математика в жизни людей?

3.         Где применяется математика?

Опрос проводился среди следующих категорий:

1.Обучающиеся 6-10 классов  (93 человек)

2. Учителя и работники  школы  (15 человек)

3. Родители школьников (21 человек)

В опросе приняли участие 129 человек.

Результаты опроса.

 

 

Число обучающихся школы, которым нравится предмет, остается не высоким. Обучающиеся, которые осознают, что изучение математики им необходимо для будущей профессии и без математики не обойтись в повседневной жизни ни куда - в основном уже в старших классах, что конечно бы хотелось, чтобы  и школьники 5-6 классов это тоже понимали.

 

 

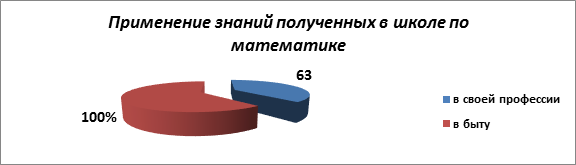
Из  опроса взрослых (родителей и коллектив школы) видно, что:

- у 63% опрошенных выбранная профессия непосредственно связана с математикой (это профессии учитель математики, учитель начальных классов, бухгалтер, повар, водитель, продавец и т.д.),  

-  100% считают, что математика применяется ими в быту и повседневной жизни.

 

5.      Заключение.

      С математикой мы встречаемся каждый день, на каждом шагу, с утра и до вечера: просыпаясь, мы смотрим на часы; в автобусе или маршрутном такси нужно рассчитаться за проезд и получить сдачу; чтобы сделать покупку в магазине, нужно снова выполнить денежные расчеты – хватит ли нам денежных средств на то  что мы решили купить, а если предлагается скидка на товар,  то нам необходимо уметь ее рассчитать; делая ремонт в квартире, нужно рассчитать, сколько купить строительных материалов и так же свой бюджет; идем в банк, чтобы положить деньги, нужно рассчитать проценты прибыли, которые мы получим; а если мы решили оформить кредит то должны понимать о том сможем ли мы из своих доходов вносить ежемесячные взносы банку по погашению долга; а если решили похудеть, то диета требует математические расчеты - надо высчитать калорийность продуктов; хотим приготовить блюдо по рецепту, нужно следовать всем пропорциям, указанным в рецепте.

Таким образом, математика одна из важных наук без неё не просто невозможно обойтись любому человеку в нашем современном мире. Математика заставляет думать, помогает человечеству открывать и использовать законы природы и в наше время является могучим двигателем науки и техники.

   То есть, наша гипотеза, что человек в повседневной жизни не может, обходится, без математических знаний подтвердилась.  Мы считаем, что математику необходимо изучать, все первоначальные знания необходимые в повседневной жизни закладываются в начальной школе.

   Таким образом, использование математических знаний является необходимой частью мира, в котором мы живем.

 

 

 

 

 

Список используемой литературы и источников.

 

 

 

1.  Аксенова. М. Д. - Энциклопедия для детей.Т. 11. Математика/ Главный ред. М.Д. Аксенова. - М. Аванта, 2000г.

2.  Глейзер.Г.И. «История математики в школе»

3.  Сергеев И.С. «Примени математику»

4.  Спивак А.В. Математический праздник. 4.1 - М.: Бюро Квантум, 2000

5.  Шалаева Г.П. Всё обо всём. Популярная энциклопедия для детей. Москва «Слово» 2005г.

6.  Материалы интернет ресурсов:

  - http://www.webmath.ru,

  - http://www.wikipedia.org,

- http://bse.sci-lib.com/article048077.html – «Золотое сечение»;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru