Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №10»

Исследовательский проект по математике

по теме: «Формула Пика»

 Выполнила:

ученица 9 «а» класса

Гурская Мария

Наставник:

Казакова Надежда Сергеевна

учитель математики

Кыштым, 2021 г.

Содержание

Введение……………………………………………………....................

Глава 1 Теория формулы Пика

1.1. Формула Пика. ………………………………………….

1.2 Решетки. Узлы………………………………….

1.2.Доказательство формулы Пика. ………………………………

Глава 2. Исследование формулы Пика

2.1.Исследование площадей многоугольников, изображенных на клетчатой бумаг………………

2.2 Эксперимент и исследование…………………………………………………………………….

2.3 Сравнительный анализ времени, затраченного на решение задач………

2.2. Геометрические задачи с практическим содержанием…....

Заключение …………………………………………………………..

Список литературы………………………………………………..

Введение

«Берем палец и считаем»

В.В.Вавилов

Увлечение математикой часто начинается с размышления над какой-то задачей. Увидев задачи в контрольно – измерительных материалах ОГЭ на нахождение площади многоугольника на клетчатой бумаге, я решила их исследовать. Возникли вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге.

Заинтересовавшись этой темой, я начала искать дополнительный материал в Интернете. В результате поисков я нашла  формулу Пика - это формула для вычисления площади многоугольника, нарисованного на клетчатой бумаге. Вычисление площади по этой формуле мне показалось доступным любому ученику. Именно поэтому я решила провести исследовательскую работу.

Актуальность: при решении задач по математике и геометрии часто встречаются задачи, где нужно вычислить площадь фигур. Если фигура сложная, то её площадь находить довольно долго. Выбор темы проекта не случаен. Способы нахождения площади многоугольника нарисованного на клетчатой бумаге очень интересная тема. Мы знаем разные способы выполнения таких заданий: способ достраивания, способ разбиения и др.

Цель: исследование рациональности использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.

Задачи:

1. Изучить доказательство теоремы Пика.

2. Изучить методы вычисления площадей сложных фигур на плоскости.

2. Научиться применять формулу Пика для вычисления площадей.

3. Сравнить и проанализировать результаты исследования.

4. Провести эксперимент, направленный на выявление эффективного способа вычисления площадей фигур по клетчатой бумаге.

5. Разработать сборник задач учащимся по применению формулы Пика при решении задач ОГЭ. 

Методы:

Системный анализ

Обобщение

Сравнение

Поиск

Гипотеза: мы считаем, что вычисление площадей сложных фигур с помощью формулы Пика легче, чем вычисление методом достраивания и разбивания фигур на части.

При решении задач на клетчатой бумаге понадобится геометрическое воображение и достаточно простые геометрические сведения, которые известны всем. При более внимательном исследовании задач на клетчатой бумаге, убеждаешься в их востребованности, оригинальности, полезности, возникает ощущение красоты, закона и порядка в природе.

Глава 1 Теория Формул Пика

1.1 Теорема Пика:

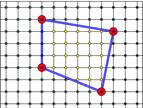
Пусть L - число целочисленных точек внутри многоугольника, B- количество целочисленных точек на его границе, S — его площадь. Тогда справедлива формула Пика: S=L+B/2-1

Для многоугольника на рисунке L=23(желтые точки), B=7(синие точки), значит S=23+3,5-1=25,5 клеток 

Доказательство:

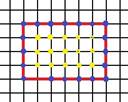
Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны X и Y . Имеем в этом случае:

•      L=(X-1)(Y-1)

•      B=2X+2Y

•     

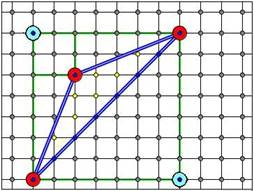
Рассмотрим прямоугольный           треугольник с катетами, II осям координат. Такой треугольник получается при разрезании прямоугольника по диагонали. Пусть на диагонали лежит С точек.

•      L=((X-1)(Y-1)-C+2)/2

•      B=X+Y+C-1

•      S=0,5XY-0,5X-0,5Y+0,5-0,5C+1+0,5X+0,5Y+0,5C-0,5-1

•      S=0,5XY-0,5X-0,5Y+0,5-0,5C+1+0,5X+0,5Y+0,5C-0,5-1

•     

Произвольный треугольник можно получить, отрезав от прямоугольника прямоугольные треугольники            и,         возможно,      прямоугольник. Поскольку и для прямоугольника, и для треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

Доказательство для многоугольника

Пусть многоугольник M и треугольник T имеют общую сторону. Предположим, что для M формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из M добавлением T. Так как M и T имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через c и получим LMT=LM+LT+(c-2) — число внутренних целочисленных точек нового многоугольника,

BMT=BM+BT-2(c-2)-2 — число граничных точек нового многоугольника.

Из этих равенств получаем

LM+LP=LMT-(c-2),BM+BP=BMT+2(c-2)+2 .

Так как мы предположили, что теорема верна для M и для T по отдельности, то SMT=SM+ST=(LM+BM/2-1)+(LT+BT/2-1)=(LM+LT)+(BM+BT)/2-2= LMT-(c-2)+(BMT+2(c-2)+2)/2-2=

=LMT+BMT/2-1 .

Тем самым, формула Пика доказана.

1.2 Решетки. Узлы.

Формула Пика справедлива для многоугольников с вершинами в узлах целочисленной решетки. На плоскости образуется решетка двумя системами параллельных равностоящих прямых. Эти прямые называются основными целочисленными прямыми, а точки их пересечения называются узлами решетки. Прямая, соединяющая два узла решетки, называется целочисленной прямой. Основные целочисленные прямые являются целочисленными линиями, но есть также много других целочисленных линий. Многоугольник, ребра которого лежат на целочисленных прямых, называется целочисленным многоугольником.

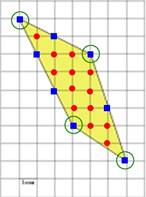
Внутренние узлы многоугольника - красные.

Узлы на гранях многоугольника - синие.

Теорема Пика утверждает, что площадь целочисленного многоугольника равна В + Г/2

- 1 , где В — число узлов решетки внутри многоугольника, а Г — число узлов решетки на границе многоугольника. Особенностью данной формулы является тот факт, что её можно применять только для многоугольников, нарисованных на клетчатой бумаге.

Чтобы оценить площадь многоугольника, нарисованного на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы примем за единицу).

2.1 Сравнительный анализ решения задач на нахождение площадей многоугольников по клетчатой бумаге по формулам планиметрии и формуле Пика

Я решила рассмотреть различные фигуры по клетчатой бумаге и найти их площадь. Провела сравнительный анализ решения задач на нахождения площадей многоугольников по клетчатой бумаге по формулам планиметрии и формуле   Пика. Мое внимание привлекли более интересные фигуры на клетчатой бумаге, площадь которых можно        найти только по формуле Пика.

 Найдите площадь окрашенной фигуры, изображенной на чертеже.

Размер каждой клетки равен 1 см * 1 см. Ответ дайте в квадратных сантиметрах

2.2 Эксперимент и исследование

Мы решили провести эксперимент для того, чтобы выяснить какой из рассмотренных способов является самым эффективным (безошибочным и малозатратным по времени). Обучающимся 9 классов мы напомнили и объяснили способы нахождения площадей     фигур на клетчатой бумаге. Каждому нужно было решить 2 задачи и засечь время их выполнения.

Затем мы рассказывали им о формуле Пика, показали на примерах её применение и  предложили решить те же задачи, но по формуле Пика (снова засекали время).

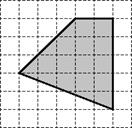
Задача 1.

1    способ: Нужно разбить фигуру на трапецию и треугольник. Найти их площади и сложить.

2 

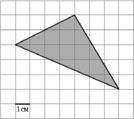
Задача 2.

1       способ: Достроить до прямоугольника, чтобы треугольник целиком в нем содержался. Найти площадь прямоугольника, площади трех прямоугольных треугольников, затем из площади прямоугольника вычесть сумму площадей трех треугольников.

2  способ: Формула Пика

2.3 Сравнительный анализ времени, затраченного на решение задач.

Результаты эксперимента:

Общие результаты эксперимента:

Проведенный эксперимент показал, что:

1)  практически никто из учеников не знал формулу Пика;

2)  12 из 20 учащихся допустили ошибки при решении задач альтернативными способами;

3)  6 из 20 учащихся допустили ошибки при решении задач, используя формулу Пика; 4) количество безошибочных работ при использовании формулы увеличилось в 2 раза.

5)  время, затраченное на решение по формуле Пика, сократилось почти в 2 раза.

6)   

Вывод: Таким образом, рассматривая задачи на нахождение площадей многоугольников, изображенных на клетчатой бумаге, по формулам геометрии и по формуле Пика и сравнивая результаты в таблицах, я показал справедливость формулы Пика и пришла к выводу, что площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по формуле геометрии.

Итак, моя гипотеза оказалась верной.

Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на бесконечном листке бумаги, расчерченном на одинаковые квадратики? Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Я научилась вычислять площади многоугольников, нарисованных на клетчатом листке.

Для многих задач на бумаге в клетку нет общего правила решения, конкретных способов и приёмов. Вот это их свойство обуславливает их ценность для развития не конкретного учебного умения или навыка, а вообще умения думать, размышлять, анализировать, искать аналогии, то есть, эти задачи развивают мыслительные навыки в самом широком их понимании.

Заключение

В результате своей работы я изучила много справочной, научно-популярной литературы, отобрала материал для исследования, проанализировала и систематизировала  полученную информацию, научилась решать задачи по формуле Пика. Провела эксперимент и доказала свою гипотезу, что вычисление площади фигуры по формуле Пика обеспечит правильное и быстрое решение задачи по сравнению с вычислением площади фигуры по формулам планиметрии. Рассмотрела различные задачи на построение и вычисления, заданные на клетчатой бумаге, подобрала нестандартные задания. Эти задачи отличаются от обычных задач, предложенных в действующих учебниках и задачниках по математике.

Любители   головоломок увлекаются   решением задач    на    клетчатой бумаге, прежде всего потому, что универсального метода решения таких задач не существует, и каждый, кто берётся за их решение, может в полной мере проявить свою смекалку, интуицию и способность к   творческому мышлению,   поскольку здесь   не   требуется глубокого знания геометрии.

Вместе с тем, задачи на клетчатой плоскости не являются несерьёзными или бесполезными, они не так уж и далеки от серьёзных математических задач.

В результате работы я расширила свои знания о решении задач на клетчатой бумаге, определила для себя классификацию исследуемых задач, убедилась в их многообразии.

Результат моей работы -это разработанный мною задачник с рекомендациями по использованию формулы Пика.

Список литературы

1.      Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7-9 классы. М. Просвещение, 2016.

2.      Геометрия на клетчатой бумаге. Малый МЕХмат МГУ.

3.      Вавилов В.В, Устинов А.В. .Многоугольники на решетках. М.МЦНМО,2006.

4.      Игнатьев Е. И. В царстве смекалки. – М.: Наука, 1982.

5.      Математические этюды.etudes.ru

6.      Семенов А.Л. ЕГЭ: 3000 задач с ответами по математике. Все задания группы В. – М.: «Экзамен», 2013гг

7.      Смирнова И. М., Смирнов В. А. Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2010.

8.      Задачи открытого банка заданий по математике ФИПИ, 2019 – 2202г.

Скачано с www.znanio.ru