Проектная работа на тему: «Путешествие в мир фракталов»

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

 «СРЕДНЯЯ ШКОЛА № 58 ГОРОДА МАКЕЕВКИ»

 

 

 

 

 

 

Проектная работа

На тему: «Путешествие в мир фракталов»

 

 

 

 

 

 

 

 

 

Работу выполнил учащийся 11-А класса Кокоша Игорь   Руководитель учитель математики Кривобок Оксана Сергеевна

 

                                                                                        

 

Макеевка

2022 год

СОДЕРЖАНИЕ

1. Паспорт проекта…………………………………………..3

2. Актуальность проекта……………………………………4

3. Цели и задачи проекта……………………………………4

4. Значимость проекта………………………………………5

5. Прогнозируемые результаты реализации проекта…...5

6.Этапы проекта……………………………………………...6

7. Использованные источники……………………………..7

8. Путешествие в мир фракталов………………...………..8

   8.1. История появления…………………………………...8

   8.2.Термин…………………………………………………..9

   8.3. Классификация………………………………………12

   8.4. Применение…………………………………………...16

Приложение 1. Галерея фракталов………………………24

Приложение 2.   Фракталы в природе…………………...26

 

 

 

 

 

 

 

ПАСПОРТ ПРОЕКТА

 

Название проекта	Путешествие в мир фракталов
Автор проекта	Кокоша Игорь Александрович, учащийся 11-А класса МБОУ «Средняя школа №58» города Макеевки
Срок реализации проекта	2021-2022
Тип проекта	Информационный (по результатам деятельности) Предметный (по направленности) Индивидуальный (по взаимодействию)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математика,

если на нее правильно посмотреть,

отражает не только истину,

но и несравненную красоту.
Бертранд Рассел

Актуальность

       С появлением фракталов со всей очевидностью стала ясна ограниченность описания природы с помощью гладких кривых, поверхностей и гиперповерхностей. Окружающий нас мир гораздо разнообразнее, и в нем оказалось немало объектов, допускающих фрактальное описание и не укладывающихся в жесткие рамки евклидовых линий и поверхностей.

       Развитие представлений фрактальной физики и геометрии позволяет объяснить многие ранее представлявшиеся необъяснимыми явления и феномены. К сожалению, наше мышление пока не приспособлено к осознанию этих понятий и тем более к их интуитивному осознанию. Мы привыкли описывать окружающий нас мир с помощью понятий классической физики, опирающихся на наши органы чувств и их восприятие.

       В работе я постарался указать, как фракталы могут быть использованы и где в природных явлениях можно ожидать возникновение самоподобных фрактальных структур.

Цели и задачи проекта

Цель проекта: познакомиться с таким математическим понятием как «фрактал», увидеть их красоту.

Задачи проекта:

·        Познакомиться с историей появления фракталов;

·        Дать определение фрактала;

·        Изучить фракталы в разных сферах жизни;

·        Увидеть мир фракталов вокруг нас.

Значимость проекта

     Данный проект -   это краткое повествование об одном из чудес современной науки - фракталах. В работе я хотел показать, что появление фрактальной геометрии есть свидетельство продолжающейся эволюции человека и расширения его способов познания и осознания мира; что когда речь заходит о науке, мы ставим не точку, а многоточие - наука продолжает жить и созидать новое знание.

 

Прогнозируемые результаты реализации проекта

Реализация проекта содействует:

v формированию у учащихся знаний о математическом понятии «фрактал»;

v получению возможности раскрыть ключевые аспекты процессов исследования и проектирования для составителя проекта;

v подготовке дополнительного материала для его использования на уроках алгебры и геометрии.

 

 

 

 

 

 

 

 

 

 

 

 

 

Этапы проекта

Этапы работы	Деятельность учащегося
1.Вступление в проект. Подготовка.	Обсуждение предмета с учителем, определение целей и задач проекта, поиск необходимой информации.
2. Планирование деятельности.	Выработка плана-алгоритма действий: определение источников информации; определение способов сбора информации, выбор способов презентации результатов; формирование представлений об ожидаемых результатах (форма устного и письменного отчета); выработка критериев оценки результата и процесса деятельности.
3. Исследование.	1. Сбор информации. 2. Решение промежуточных задач. 3. Работа с источниками.
4. Оформление отчета. Подготовка к презентации.	1. Обобщение и классификация собранных результатов. 2. Изготовление иллюстративного материала (фотографии, рисунки). 3. Подготовка презентационных информативных материалов и окончательное оформление продуктов проекта.
5.Презентация результатов исследования. Защита проекта.	Показ результатов в форме устного отчета, письменного отчета  информационного пакета результатов проекта.
6. Итоги. Рефлексия. Оценка проектной деятельности и ее результатов.	1.Подведение итогов. 2. Самооценка результатов и процесса исследования по установленным критериям.

 

Использованные источники

1. https://allatravesti.com/

2. https://yandex.ua/

3. https://ru.wikipedia.org/

4. https://nsportal.ru/

5. https://infourok.ru/

6. http://codenet.ru/

7. Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.

8. Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.

 

 

 

 

 

 

 

 

 

 

 

 

 

Путешествиев мир фракталов

 История появления

       Первые идеи фрактальной геометрии возникли в 19 веке. Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками. Пеано нарисовал особый вид линии (рисунок №1). Для ее рисования Пеано использовал следующий алгоритм.

       На первом шаге он брал прямую линию и заменял ее на 9 отрезков длинной в 3 раза меньшей, чем длинна исходной линии. Далее он делал то же самое с каждым отрезком получившейся линии. И так до бесконечности. Ее уникальность в том, что она заполняет всю плоскость. Доказано, что для каждой точки на плоскости можно найти точку, принадлежащую линии Пеано. Кривая Пеано и пыль Кантора выходили за рамки обычных геометрических объектов. Они не имели четкой размерности. Пыль Кантора строилась вроде бы на основании одномерной прямой, но состояла из точек (размерность 0). А кривая Пеано строилась на основании одномерной линии, а в результате получалась плоскость. Во многих других областях науки появлялись задачи, решение которых приводило к странным результатам, на подобие описанных выше (Броуновское движение, цены на акции).

         

Рис. 1. Пыль Кантора                                   Рис. 2. Кривая Пеано

 

 

 Термин

 

Отец фракталов

  

       Вплоть до 20 века шло накопление данных о таких странных объектах, без какой либо попытки их систематизировать. Так было, пока за них не взялся Бенуа Мандельброт - отец современной фрактальной геометрии и слова фрактал. Работая в IBM математическим аналитиком, он изучал шумы в электронных схемах, которые невозможно было описать с помощью статистики. Постепенно сопоставив факты, он пришел к открытию нового направления в математике - фрактальной геометрии.

      В 1975 году Мандельброт опубликовал свою работу Какова длина побережья Великобритании? — первое исследование фракталов^]. Понятие «фрактал» придумал сам Бенуа Мандельброт). Используя находящиеся в его распоряжении компьютеры IBM, Мандельброт создал графические изображения, сформированные на основе множества Мандельброта. По словам математика, он не чувствовал себя изобретателем, несмотря на то, что никто до него не создавал ничего подобного. 

Что такое фрактал

       Что такое фрактал? Как устроен мир вокруг нас? Что лежит в основе всего? Почему наша Галактика по форме похожа на раковину Наутилуса, человеческий глаз на космическую туманность, а клетки мозга на всю нашу Вселенную?

       Кому из вас не доводилось видеть похожие формы в живых и неживых объектах? Будто одна и та же формула, пронизывает всё вокруг. 

       Что же такое фрактал?  Сам Мандельброт вывел слово fractal от латинского слова fractus, что означает разбитый (поделенный на части). И одно из определений фрактала - это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого (по крайней мере, приблизительно).  

       Можно сказать, что фрактал – это узор, который повторяет сам себя в разных масштабах до бесконечно малого или/и бесконечно большого. Он рождается не просто повторением форм, а скорее повторением процесса, который применяется к форме. Бесконечная цепочка самопостроения.

       Чтобы представить себе фрактал понаглядней рассмотрим пример, приведенный в книге Б.Мандельброта "The Fractal Geometry of Nature" ("Фрактальная геометрия природы") ставший классическим - "Какова длина берега Британии?". Ответ на этот вопрос не так прост, как кажется. Все зависит от длины инструмента, которым мы будем пользоваться. Померив берег с помощью километровой линейки мы получим какую-то длину. Однако мы пропустим много небольших заливчиков и полуостровков, которые по размеру намного меньше нашей линейки. Уменьшив размер линейки до, скажем, 1 метра - мы учтем эти детали ландшафта, и, соответственно длина берега станет больше. Пойдем дальше и измерим длину берега с помощью миллиметровой линейки, мы тут учтем детали, которые больше миллиметра, длина будет еще больше. В итоге ответ на такой, казалось бы, простой вопрос может поставить в тупик кого угодно - длина берега Британии бесконечна.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Классификация

 

Фракталы делятся на группы. Самые большие группы это:

* геометрические фракталы

* алгебраические фракталы

* стохастические фракталы.

 

Геометрические фракталы.

       Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется "затравка" - аксиома - набор отрезков, на основании которых будет строиться фрактал. Далее к этой "затравке" применяют набор правил, который преобразует ее в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем (по крайней мере, в уме) бесконечное количество преобразований - получим геометрический фрактал.

       Примерами таких фракталов являются треугольник Серпинского, снежинка Коха, кривая Леви и многие другие.

 

Рис.3  Снежинка Коха

    

Рис.4 Треугольник Серпинского                    Рис. 5 Кривая Леви

       Из этих геометрических фракталов очень интересным и довольно знаменитым является первый - снежинка Коха. Строится она на основе равностороннего треугольника. Каждая линия которого ___ заменяется на 4 линии каждая длинной в 1/3 исходной _/\_. Таким образом, с каждой итерацией длинна кривой увеличивается на треть. И если мы сделаем бесконечное число итераций - получим фрактал - снежинку Коха бесконечной длинны. Получается, что наша бесконечная кривая покрывает ограниченную площадь.

Алгебраическиефракталы.
       Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:

1.     С течением времени стремится к бесконечности.

2.     Стремится к 0

3.     Принимает несколько фиксированных значений и не выходит за их пределы.

4.     Поведение хаотично, без каких либо тенденций.

       Чтобы проиллюстрировать алгебраические фракталы обратимся к классике - множеству Мандельброта.

     

 

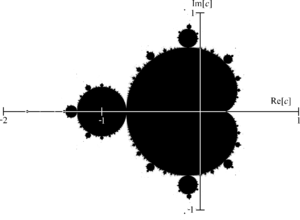
Рис. 6. Множество Мандельброта             Рис.7. Фрагмент границы множества  

                                                                                  в цветном варианте

Стохастические фракталы.

Типичный представитель данного класса фракталов "Плазма".

    

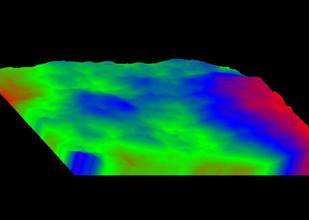
Рис. 8. Плазма

       Для ее построения возьмем прямоугольник и для каждого его угла определим цвет. Далее находим центральную точку прямоугольника и раскрашиваем ее в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число - тем более "рваным" будет рисунок. Если мы теперь скажем, что цвет точки это высота над уровнем моря - получим вместо плазмы - горный массив. Именно на этом принципе моделируются горы в большинстве программ. С помощью алгоритма, похожего на плазму строится карта высот, к ней применяются различные фильтры, накладываем текстуру и пожалуйста фотореалистичные горы готовы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V. Практическое применение фракталов

       Фракталы доказали свою пользу в ряде прикладных областей. Фракталы используются при анализе и классификации сигналов сложной формы, возникающих в разных областях, например при анализе колебаний курса валют в экономике. Они применяются в физике твердого тела, в динамике активных сред. Также в настоящее время фракталы используются для сжатия изображений.

       Поскольку фракталы позволяют с помощью всего лишь нескольких коэффициентов определить сложные линии и поверхности, то их лучшим применением оказывается создание таких фонов, как облака, горы, поверхности моря. Поэтому фракталами должны владеть как разработчики игр, так и разработчики различных тренажеров. Ведь практически в любой игре вы ощущаете их присутствие. Широкое применение фракталы находят при оживлении (анимации) изображений на Web. Создание медленных волн на воде или расходящихся кругов от капель дождя - вот только некоторые яркие примеры использования фракталов.

       Подобно тому как композитор садится к роялю и начинает наигрывать в поисках новой мелодии, так и работа с абстрактными узорами, получаемыми с помощью фракталов, может стимулировать художников в их творческих планах. Попробуйте, тогда и вы сами, и ваши друзья и малые дети - никто не сможет оторваться от завораживающего зрелища.

       Роль фракталов в интенсивных научных исследованиях в сегодняшнем мире достаточно велика. Фракталы используются в медицине, биологии, метеорологии, физике полимеров, геоморфологии, теории турбулентности, теории броуновского движения и т.п.

       Фракталы находят все большее и большее применение в науке. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Вот несколько примеров:

1. КОМПЬЮТЕРНЫЕ СИСТЕМЫ

       Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом, картинки сжимаются гораздо лучше, чем это делается обычными методами (такими как jpeg или gif).

       Другое преимущество фрактального сжатия в том, что при увеличении картинки, не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.

2. МЕХАНИКА ЖИДКОСТЕЙ

       Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к из фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков.

       При помощи фракталов также можно смоделировать языки пламени.

       Пористые материалы хорошо представляются в фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в нефтяной науке.

3. ТЕЛЕКОММУНИКАЦИИ

       Для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес.

       Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка на зданиях внешних антенн. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, а затем присоединил к приёмнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы работы такой антенны не изучены до сих пор, это не помешало Коэну основать собственную компанию и наладить их серийный выпуск.

4. ФИЗИКА ПОВЕРХНОСТЕЙ. 

       Фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов.

5. МЕДИЦИНА

1 Биосенсорные взаимодействия

2 Биения сердца

3 Беспорядочная жизнь.

       Похоже, предположение инженера Корохова о "конструкции" жизни как совокупности фрактальных структур не так уж невероятно. Тому подтверждение - недавно опубликованные в США результаты оригинального исследования, ставшие своего рода научной сенсацией, ибо из них следовал вывод, опровергающий представления, укоренившиеся в медицине за последние, по крайней мере, 50 лет. Поиск вёлся там, где никто никогда не искал, - изучались фрактальные свойства физиологических систем.

Но к фракталам два доцента Гарвардского университета, Эри Л.Голдбергер, Дейвид Р.Ригни, и профессор физики Университета Северного Техаса Бруст Дж.Уэст пришли несколько позже. Первоначально они искали периодичные закономерности, которые могли бы служить индикаторами развивающихся заболеваний, в частности сердечных. При этом ученые опирались на общепризнанную концепцию гомеостаза, согласно которой все физиологические системы организма стремятся возвратиться в состояние

устойчивого равновесия, как только перестаёт действовать фактор, выводящий их из этого состояния. С такой позиции объясняются, например, нарушения сердечного ритма у старых и больных людей - ослабленному организму труднее поддерживать стабильность сокращений сердечной мышцы. Поэтому считалось: чем ярче выражена аритмия, тем вернее перспектива внезапной остановки сердца. Хотя кардиологам известны значительные даже у здоровых людей изменения частоты пульса в продолжение дня: от 40, иногда от 20 до 180 ударов в минуту. Согласно концепции гомеостаза подобные вариации - просто ответные реакции на изменения в окружающей среде.

        Экспериментаторы, обследовав в течение суток добровольцев, отличавшихся "космическим" здоровьем и защищённых, насколько возможно, от внешних раздражителей, получили на первый взгляд совершенно случайный, нерегулярный график сердечных сокращений, не несший никакой информации о предмете их поиска - периодичных закономерностях. Однако, проанализированный в различных временных масштабах, он неожиданно "заговорил". Так, на участке кривой, соответствующей нескольким часам, обнаружились более быстрые флуктуации, диапазон и последовательность которых походили на более медленные флуктуации исходного часового графика. В минутном масштабе находились ещё более быстрые флуктуации, которые также соответствовали характеристикам исходной кривой. Флуктуации выглядели подобными самим себе, так же как ветки геометрического фрактала. Предписанное теорией стремление к гомеостатической стабильности не наблюдалось.

Динамическая система вела себя неравномерно даже без изменений со стороны внешних стимулов.

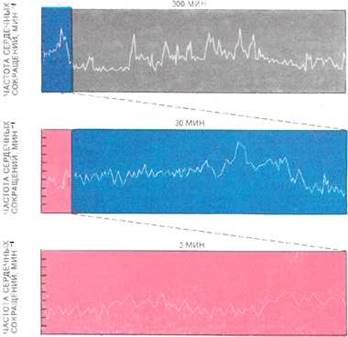
       Когда сердечный ритм здорового человека регистрируется в интервалах 300, 30 и 3 минуты, быстрые флуктуации выглядят почти так же, как медленные.

     Итак, если кардиограмма - фрактальная кривая, то, во-первых, причиной её

самоподобия в отсутствие внешних раздражителей должно быть устройство и условия жизнедеятельности самого организма, а во-вторых, признаком здоровья становился не стабильный сердечный ритм, а повторяющиеся в разных масштабах скачки амплитуды сердечных сокращений.

 

 

 

 

 

 

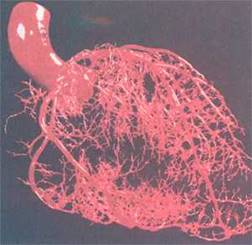
        Подтверждение первого вывода напрашивалось само собой. Ведь сердце снабжается кровью с помощью фракталоподобной структуры артерий и вен. В самом сердце ветвящиеся сухожилия прикрепляют митральный и трехстворчатый клапаны к мышцам. Наконец, фрактальная организация прослеживается в картине разветвления некоторых сердечных мышечных волокон и в так называемой системе Гиса, передающей электрические сигналы от предсердий к желудочкам.

       Если ещё учесть, что управляющие "механизмом" сердца нервные клетки с их расходящимися на всё более мелкие волокна отростками-дендритами являют пример типичного фрактала, то наблюдение гарвардцев и техасца становится вполне объяснимым.

       Второй вывод требовал экспериментального подтверждения. И через несколько месяцев, проведенных учёными в клинике возле кардиографов, доказательства были получены Тогда-то и окрепли сомнения в абсолютной справедливости положений теории гомеостаза. Полученные графики оказались красноречивее любых слов. На одном из них сердечный ритм почти стабилен. Получен он за 13 часов до... остановки сердца. На другом заметна его явная упорядоченность, произошедшая за 8 суток до внезапной смерти от сердечной недостаточности. И, наоборот, кривая сердцебиения здорового человека отличается "болезненной" хаотичностью.

        Получалось, что вопреки сложившимся представлениям беспорядок означал жизнь, а выраженная стабильность предрекала близкую смерть. Но почему природа противоречит здравому смыслу, предпочитая рациональному порядку непредсказуемый хаос? Вероятно, потому, что, с её точки зрения, хаос и есть вершина рациональности. Ведь хаотическая динамика даёт организму много функциональных преимуществ. Благодаря этому он способен работать в широком диапазоне условий и легко адаптироваться к изменениям. Пластичность позволяет учитывать требования постоянно изменяющейся внешней среды. Динамику "случайности" обеспечивают фрактальные структуры, обладающие к тому же и значительным запасом прочности.

       Физиологам ещё предстоит лучше понять то, каким образом эволюция приводит к возникновению фрактальных структур и как динамические процессы в организме порождают наблюдаемые признаки хаоса. В недалеком будущем благодаря изучению фракталов, возможно, возникнут более тонкие методы анализа различных нарушений функций организма при старении, заболеваниях, употреблении лекарств с побочным действием.

6. БИОЛОГИЯ

       Моделирование хаотических процессов, в частности при описании моделей популяций.

 

 

 

 

 

 

 

7. КОМПЬЮТЕРНАЯ ГРАФИКА

       Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и т. д.

8. ЭКОНОМИКА

     В последнее время фракталы стали популярны у «трейдеров» для анализа курса фондовых бирж, валютных и торговых рынков.

 

9. ФИЗИКА И ДРУГИЕ ЕСТЕСТВЕННЫЕ НАУКИ

       В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Также фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

10. ЛИТЕРАТУРА

       Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой. В текстуальных фракталах потенциально бесконечно повторяются элементы текста неразветвляющееся бесконечное дерево, тождественные самим себе с любой итерации («У попа была собака…», «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится…», «Ложно утверждение, что истинно утверждение, что ложно утверждение…») неразветвляющиеся бесконечные тексты с вариациями («У Пегги был весёлый гусь…») и тексты с наращениями («Дом, который построил Джек»).

         В структурных фракталах схема текста потенциально фрактальна венок сонетов (15 стихотворений), венок венков сонетов (211 стихотворений), венок венков венков сонетов (2455 стихотворений), «рассказы в рассказе» («Книга тысячи и одной ночи», Я.Потоцкий «Рукопись, найденная в Сарагоссе»)

 

 

 

 

ПРИЛОЖЕНИЕ 1

Галерея фракталов

ПРИЛОЖЕНИЕ 2

Фракталы в природе

 

 

 

Скачано с www.znanio.ru