
Программа элективного курса
«Задачи, содержащие переменную под знаком модуля»
Составила учитель математики
Милаенко Е.В.
Пояснительная записка
Создание программы данного
курса вызвано тем, что в школьном курсе математики учащиеся знакомятся лишь с понятием
модуля и учатся решать лишь уравнения вида ![]() ,
где
,
где ![]() - постоянная величина. Поэтому
задачи, в которых присутствует модуль, вызывают у учащихся затруднения, они не
имеют соответствующих умений и навыков по этой теме.
- постоянная величина. Поэтому
задачи, в которых присутствует модуль, вызывают у учащихся затруднения, они не
имеют соответствующих умений и навыков по этой теме.
Предложенный курс «Задачи, содержащие переменную под знаком модуля», знакомит учащихся с основными свойствами модуля, основными типами уравнений и неравенств, содержащих переменную под знаком модуля. Этот курс позволяет учащимся выработать умение применять определение и свойства модуля для преобразования выражений, нахождения их значений, решения уравнений, содержащих переменную под знаком модуля.
Цель программы: создание ориентационной и мотивационной основы учащихся, направленных на:
-овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
-интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе.
Программа рассчитана на 16 учебных часов.
Направлена на подготовку учащихся к выпускным и вступительным экзаменам и на то, чтобы учащиеся могли использовать приобретённые знания и умения в практической деятельности, в повседневной жизни.
· сформировать понятие о модуле, его свойствах, границах их применения;
· способствовать интеллектуальному развитию учащихся, формированию качеств мышления, характерных для математической деятельности.
· сформировать умение применять определение модуля для упрощения выражений, содержащих переменную под знаком модуля;
· сформировать умение решать уравнения, содержащие переменную под знаком модуля.
Данный курс рассчитан на 16 часов, предполагает изучение теории по теме, решение задач и самостоятельную работу учащихся.
Преподаватель предложенную подборку теории и задач может изменять как в сторону увеличения, так и в сторону уменьшения, в зависимости от состава учащихся.
Программа может быть использована в 9-11 классах.
В результате изучения курса учащиеся должны
· понимать определение модуля;
· уметь применять определение и свойства модуля.
|
№ п/п |
Содержание материала |
К-воча-сов |
Рекомендуемая литература |
|
|||||||
|
1 |
2 |
3 |
|
||||||||
|
1,2
3-5
6,7
8-12
13-15
16 |
Определения и свойства модуля.
Преобразование выражений, со-держащих переменную под зна-ком модуля.
Построение графиков функций, содержащих переменную под знаком модуля.
Решение уравнений, содержащих переменную под знаком модуля.
Решение неравенств, содержащих переменную под знаком модуля.
Итоговое занятие. |
2
3
2
5
3
1 |
Стр.7
Стр.15-24
Стр.25-73, 74-129 |
Стр.5
Стр.5,6
Стр.14-25 |
Стр. 34
Стр.34-48, 128-143 |
||||||
для нахождения значений выражений, содержащих переменную под знаком
модуля.
Формировать понятие о свойствах модуля и умение применять их в различных ситуациях.
2. Преобразование выражений, содержащих переменную под знаком модуля
(3 часа).
Формировать умение применять определения и свойства модуля, для преобра-
зования выражений, содержащих переменную под знаком модуля, нахождения
значений таких выражений.
3. Построение графиков функций, содержащих переменную под знаком модуля( 2 часа).
4. Решение уравнений, содержащих переменную под знаком модуля (5 часов).
Формировать умение решать уравнения, содержащие переменную под знаком модуля.
5. Решение неравенств, содержащих переменную под знаком модуля (3 часа).
6. Итоговое занятие.(1час).
Материалы для учителя
1. Определение и свойства модуля.
Опр. Абсолютной величиной числа ![]() (модулем числа
(модулем числа ![]() ) называется расстояние от точки, с
координатой
) называется расстояние от точки, с
координатой ![]() , на числовой прямой, до начала
отсчёта.
, на числовой прямой, до начала
отсчёта.
Обозначают абсолютную
величину числа ![]() как
как ![]() .
.
Из определения модуля
следует, что 
Свойства модуля.
1) ![]() ;
7)
;
7)![]() ;
;
2) ![]() ;
8)
;
8) ![]() , тогда и только тогда, когда
, тогда и только тогда, когда ![]() ;
;
3) ![]() ; 9)
; 9) ![]() , тогда и только тогда, когда
, тогда и только тогда, когда ![]() и
и
![]() ;
;
4) ![]() ; 10)
; 10) ![]() , тогда и только тогда, когда
, тогда и только тогда, когда![]() ;
;
5) ![]() ,
, ![]() ;
11)
;
11)![]() , тогда и только тогда, когда
, тогда и только тогда, когда![]() .
.
6) ![]() ;
;
Упражнения для самостоятельной работы.
Раскройте знак модуля:
1.
![]() ;
5.
;
5. ![]() ; 9.
; 9. ![]() ; 13.
; 13. ![]() ;
;
2.
![]() ;
6.
;
6. ![]() ; 10.
; 10. ![]() ; 14.
; 14. ![]() ;
;
3.
![]() ;
7.
;
7. ![]() ; 11.
; 11. ![]() ; 15.
; 15. 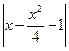 .
.
4.
![]() ;
8.
;
8. ![]() ; 12.
; 12. ![]() ;
;
Решите уравнения:
1.
![]() ; 6.
; 6. ![]() ; 11.
; 11. ![]() ;
;
2.
![]() ; 7.
; 7. ![]() ; 12.
; 12. ![]() .
.
3.
![]() ; 8.
; 8. ![]() ;
;
5.
![]() ;
9.
;
9. ![]() ;
;
6.
![]() ;
10.
;
10. ![]() ;
;
Решите неравенство:
1.
![]() ;
4.
;
4. ![]() ; 7.
; 7. ![]() ; 10.
; 10. ![]() ;
;
2.
![]() ;
5.
;
5. ![]() ; 8.
; 8. ![]() ; 11.
; 11. ![]() ;
;
3.
![]() ;
6.
;
6. ![]() ; 9.
; 9. ![]() ; 12.
; 12. ![]() .
.
2. Преобразования рациональных выражений
Тождественное преобразование выражений, содержащих переменную под знаком модуля, состоит в разбиении их области допустимых значений на промежутки знакопостоянства, в каждом из которых освобождаются от модуля по определению последнего, а затем упрощают выражение, не содержащее модуля.
№1.
Упростить выражение А=![]() .
.
Решение. Область допустимых значений данного выражения – все действитель-ные числа.
Найдём значения переменной, при которых каждый из модулей равен нулю:
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Этими значениями переменной множество всех действительных чисел разбива-ется на три промежутка, на каждом из которых выражения стоящие под знаком модуля не меняют свой знак.
1)
![]() ,
,
![]() ,
, ![]() ,
,
![]() ;
;
2) ![]() ,
, ![]() ,
,
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Ответ. Если ![]() , то А=
, то А=![]() ;
;
если ![]() ,
тоА=
,
тоА=![]() ;
;
если ![]() , тоА=
, тоА=![]()
![]() .
.
№2. Упростить выражение А=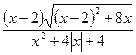 .
.
Решение. А=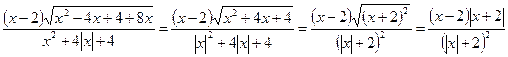 .
.
Область допустимых значений данного выражения – все действительные числа.
Найдём значения переменной, при которых каждый из модулей равен нулю:
![]() ,
,
![]() ;
; ![]() .
.
Этими значениями переменной множество всех действительных чисел разбива-ется на три промежутка, на каждом из которых выражения стоящие под знаком модуля не меняют свой знак.
1)
![]() ,
,![]() ,
, ![]() ,
,
А=![]() ;
;
2)![]() ,
,
![]() ,
, ![]() ,
,
А=![]() ;
;
3)![]() ,
,
![]() ,
, ![]() ,
,
А=![]() .
.
Ответ. Если ![]() , то А=
, то А=![]() ;
;
если ![]() , то А=
, то А=![]() ;
;
если ![]() , то А=
, то А=![]()
![]() .
.
№3. Упростить выражение А=![]() , где
, где ![]() .
.
Решение. А=![]() =
=![]() .
.
Так как ![]() , то
, то ![]() ,
значит,
,
значит, ![]() ,
поэтому А=
,
поэтому А=![]() .
.
Ответ. ![]() .
.
№4. Упростить выражение А=![]() .
.
Решение.Так как ![]() при
при ![]() ,
то
,
то ![]() при
при ![]() ;
;
![]() ,
,
![]() ,
, ![]() .
.
1)![]() ,
, ![]() ,
,
А=![]() ;
;
2)![]() ,
, ![]() ,
,
А=![]() .
.
Ответ. Если ![]() , то А=1;
, то А=1;
если ![]() , то А=
, то А=![]() .
.
1.
![]() ;
4.
;
4. ![]() ; 7.
; 7.
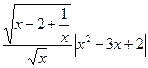 ;
;
2.
![]() ;
5.
;
5. ![]() ;
8.
;
8. ![]() ;
;
3.
![]() ;
6.
;
6. ![]() при
при ![]() ;
9.
;
9. 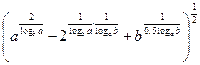 .
.
3. Решение уравнений, содержащих переменную под знаком модуля.
1). Уравнения вида ![]() (с – число).
(с – число).
Алгоритм решения таких уравнений следующий:
1) если с >![]() 0,
то
0,
то ![]() или
или ![]() ;
;
2) если с < 0, то решений нет;
3) если с = 0, то ![]() .
.
№1. Решить уравнение ![]() .
.
Решение.
![]()
![]() или
или ![]() .
.
Ответ. 1;4.
№2. Решить уравнение ![]() .
.
Решение.
Так как ![]() при
при ![]() , то данное уравнение корней не имеет.
, то данное уравнение корней не имеет.
Ответ. ![]()
![]()
№3. Решить уравнение ![]() .
.
Решение.

![]()
Ответ. –1;2;3;6.
Решите уравнения:
1.![]() =
=![]() Ответ.-2; 4.
Ответ.-2; 4.
2.![]() =
=![]() Ответ.-4; 2.
Ответ.-4; 2.
3.![]() Ответ.-0,5; 0,5.
Ответ.-0,5; 0,5.
4.![]() Ответ.-1; 4.
Ответ.-1; 4.
5.![]() Ответ.
Ответ.![]() ;
; ![]() .
.
2). Уравнения вида ![]() .
.
По свойству модуля имеем ![]()
![]()
![]()
№1. Решить уравнение ![]()
Решение.![]()
Ответ.![]()
№2. Решить уравнение ![]() .
.
Решение.![]()
Ответ.![]()
№3. Решить уравнение ![]()
Решение.![]()
Ответ. ![]() .
.
Решите уравнения:
6. ![]() Ответ.
Ответ.
![]()
7.![]() Ответ.
Ответ. ![]()
![]()
8.![]() Ответ.
Ответ. ![]()
9.![]() Ответ.
Ответ. ![]()
10.![]() Ответ.
Ответ. ![]()
3). Уравнения вида ![]() .
.
По свойству модуля решение уравнения сводится к решению совокупности уравнений:
если ![]() , то
, то ![]()
№1.Решить уравнение ![]()
Решение.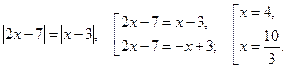
Ответ. ![]()
№2.![]()
Решение. 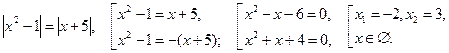
Ответ.![]()
Решите уравнения:
11.![]() Ответ.
Ответ. ![]()
12.![]() Ответ.
Ответ. ![]()
13.![]() Ответ.
Ответ. ![]()
14.![]() Ответ.
Ответ. ![]()
4). Уравнения вида![]()
![]() .
.
Если ![]() , то
, то 
№1.Решить уравнение ![]()
Решение. Это уравнение равносильно следующей системе


![]() .
.
Ответ:![]()
№2. ![]()
![]()
Решение. 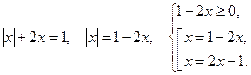 Решив
эту систему, получим что
Решив
эту систему, получим что ![]()
Ответ:![]()
Решите уравнения:
15.![]() Ответ.
Ответ. ![]()
16.![]() Ответ.
Ответ. ![]()
17.![]() Ответ.
Ответ. ![]()
18.![]() Ответ.
Ответ. ![]()
19.![]() Ответ.
Ответ. ![]()
В ответе запишите сумму корней.
20. Ответ.
Ответ. ![]()
5). Уравнения, решаемые подстановкой (заменой переменной).
Одним из эффективных методов решения уравнений различных типов является метод подстановки, при котором данное уравнение сводится к более простому виду относительно новой переменной.
При применении
подстановки для решения уравнений с модулями часто используется следующее
свойство ![]() , позволяющее данное уравнение с модулями сводить к уравнению без
модуля относительно новой переменной.
, позволяющее данное уравнение с модулями сводить к уравнению без
модуля относительно новой переменной.
№1. Решить уравнение ![]()
Решение. Введем подстановку ![]()
![]()
Тогда уравнение принимает вид
![]()
![]() значит,
значит, ![]()
Ответ: ![]()
Решите уравнения:
21. ![]() Ответ.
Ответ.
![]()
22. ![]() Ответ.
Ответ. ![]()
23. ![]() Ответ.
Ответ.
![]()
24. ![]() .
Ответ.
.
Ответ. ![]()
25.  Ответ.
Ответ. ![]()
8). Уравнения вида ![]() где
где ![]()
![]() .
.
![]() где
где ![]()
![]() , тогда и только тогда, когда
, тогда и только тогда, когда ![]()
№1. ![]()
Решение. Т.к. ![]() и
и ![]() , то
, то

Ответ: ![]()
№2. ![]()
Решение. ![]()
Это уравнение равносильно следующей системе
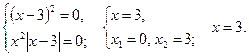
Ответ: ![]()
Решите уравнения:
26. ![]() Ответ.
Ответ. ![]()
27. ![]() Ответ.
Ответ. ![]()
28. ![]() Ответ.
Ответ. ![]()
6). Уравнения со «сложным» модулем
Будем называть «сложным» модулем такое выражение, в котором под знаком модуля находится функция, в записи которой – один или несколько модулей. Уравнения указанного в названии вида решаются, как правило, методом интервалов или применением рассмотренных выше свойств модуля.
Решим следующие уравнения
№1. ![]()

Ответ: ![]()
№2. ![]()
Решение. Т.к. ![]() при
при![]() , то
, то ![]() при
при![]() . Таким образом,
уравнение не имеет решений.
. Таким образом,
уравнение не имеет решений.
Ответ: ![]()
Решите уравнения:
29. ![]() Ответ.
Ответ. ![]()
30. ![]() Ответ.
Ответ. ![]() .
.
31. ![]() Ответ.
Ответ. ![]()
32. ![]() Ответ.
Ответ. ![]()
7). Уравнения общего вида.
№1.
Решить уравнение![]()
Решение.
Данное уравнение равносильно совокупности двух систем
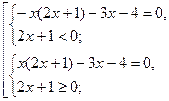

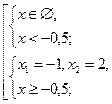
![]()
![]() .
.
Ответ: 2.
№2.
Решить уравнения: ![]()
![]()
Решение.
Данное уравнение равносильно совокупности двух систем
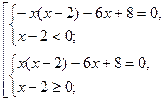
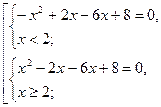
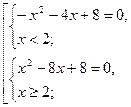
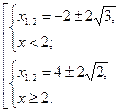
Первой
системе удовлетворяют оба решения, а второй только ![]() ,
т.к.
,
т.к. ![]() .
.
Ответ.-2![]()
![]() ,
, ![]() .
.
Подчеркнем, что выбор того
или иного из двух предложенных путей решения уравнения вида ![]() связан
лишь с вопросом, какие из неравенств
связан
лишь с вопросом, какие из неравенств ![]() или
или ![]() решить легче.
решить легче.
№4.![]()
Решение.
Находим интервалы
знакопостоянства трехчленов ![]() и
и ![]() :
:
![]() ;
; ![]() ;
;

![]() + + 1 - 3
+ +
+ + 1 - 3
+ + ![]()
![]() + - - - +
+ - - - +
![]()
![]() -1 5
-1 5
значит, данное уравнение равносильно совокупности пяти систем:
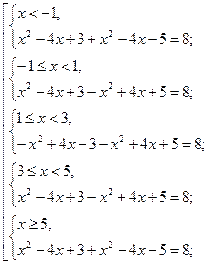
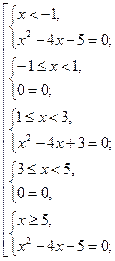
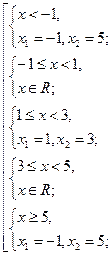
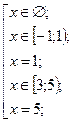
![]()
Объединяя полученные результаты, имеем
Ответ.![]() или
или
![]()
Решите уравнения:
33. ![]() .
Ответ. -6;2.
.
Ответ. -6;2.
34. ![]() .
Ответ.
.
Ответ. ![]() .
.
35. ![]() Ответ.
1;3.
Ответ.
1;3.
4. Решение неравенств, содержащих переменную под знаком модуля.
1). Неравенства вида ![]() и
и ![]() .
.
Из определения модуля
следует, что если ![]() ,
то
,
то
из того, что ![]() , следует, что
, следует, что ![]() ,
,
а из того, что ![]() , следует, что
, следует, что ![]() или
или ![]()
Если же ![]() , то из того, что
, то из того, что ![]() следует, что
следует, что![]() ,
,
а из того, что ![]() , следует, что
, следует, что ![]() - любое число из области допустимых значений
неравенства.
- любое число из области допустимых значений
неравенства.
Если ![]() , то из того, что
, то из того, что ![]() следует, что
следует, что![]() ,
,
а из того, что ![]() , следует, что
, следует, что ![]() - любое число из области допустимых значений
неравенства, кроме тех, при которых
- любое число из области допустимых значений
неравенства, кроме тех, при которых ![]() .
.
№1. Решите нравенство ![]() .
.
Решение. ![]() ,
, ![]()
![]() .
.
Ответ. ![]() .
.
№2. Решите нравенство ![]() .
.
Решение.![]()
![]()
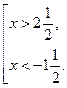
Ответ.![]() .
.
№3. Решите нравенство ![]() .
.
Решение.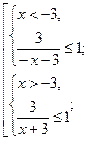
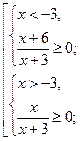
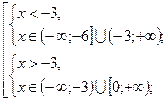
![]()
Ответ.![]() .
.
Решите неравенства:
1. ![]() .
Ответ.
.
Ответ. ![]() .
.
2. ![]() . Ответ.
. Ответ. ![]() .
.
3.
![]() .
Ответ.
.
Ответ. ![]() .
.
4.
![]() .
Ответ.
.
Ответ. ![]() .
.
5.
![]() .
Ответ.
.
Ответ. ![]() .
.
6.
![]() .
Ответ.
.
Ответ. ![]() .
.
7. ![]() .
Ответ.
.
Ответ. ![]() .
.
8. ![]() .
Ответ.
.
Ответ. ![]() .
.
2). Неравенства вида ![]() и
и
![]() .
.
Если ![]() , то
, то ![]() ;
;
если ![]() , то
, то ![]() ;
;
если ![]() , то
, то ![]()
если ![]() , то
, то ![]()
№1. Решите неравенство ![]() .
.
Решение. ![]() ,
,
![]()
![]()

![]() .
.
Ответ. ![]() .
.
№2. Решите неравенство ![]() .
.
Решение.![]()
![]()
![]()
![]() .
.
Ответ.![]() .
.
№3. Решите неравенство ![]() .
.
Решение.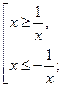

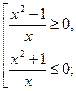
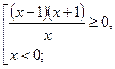
![]()
![]() .
.
Ответ.![]() .
.
Решите неравенства:
9. ![]() . Ответ.
. Ответ. ![]() .
.
10. ![]() . Ответ.
. Ответ. ![]() .
.
11. ![]() . Ответ.
. Ответ. ![]() .
.
12. ![]() . Ответ.
. Ответ.![]() .
.
2). Неравенства вида ![]() и
и ![]() .
.
Если ![]() , то
, то ![]() и
и ![]() ;
;
если ![]() , то
, то ![]() и
и
![]() .
.
№1. Решите неравенство ![]() .
.
Решение. ![]() ,
,
![]() ,
,
![]() .
.
Ответ.![]() .
.
№2. Решите неравенство ![]() .
.
Решение.![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() + - + -
+
+ - + -
+
-4 -1 ![]() 4
4 ![]()
Ответ. ![]() .
.
Решите неравенства:
13. ![]() . Ответ.
. Ответ.![]() .
.
14. ![]() . Ответ.
. Ответ.![]() .
.
15. ![]() . Ответ.
. Ответ.![]() .
.
16.![]() . Ответ.
. Ответ. ![]() .
.
3). Неравенства, решаемые с помощью введения новой переменной.
№1. Решите неравенство.![]() .
.
Решение. Так как по свойству
модуля ![]() , данное неравенство можно представить в виде
, данное неравенство можно представить в виде ![]() .
.
Пусть ![]() , тогда неравенство примет вид
, тогда неравенство примет вид
![]()
![]() ,
, ![]() ,
+ - +
,
+ - + ![]() ;
;
0 1 ![]()
значит, ![]() ,
, ![]() .
.
Ответ.![]() .
.
№2. Решите неравенство ![]() .
.
Решение. 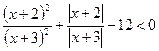 ,
,
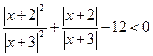 ,
,
![]() ,
,
пусть ![]() , тогда неравенство примет вид
, тогда неравенство примет вид
![]() ,
,
![]()
![]() , + - + ,
, + - + , ![]() , так как
, так как ![]() ,
то
,
то
-4 3 ![]()
![]() ,
поэтому
,
поэтому
![]() ,
, 
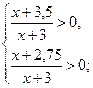
![]()
![]() .
.
Ответ. ![]() .
.
Решите неравенства:
17. ![]() . Ответ.
. Ответ.![]() .
.
18. ![]() . Ответ.
. Ответ.![]() .
.
19. 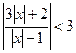 . Ответ.
. Ответ.![]() .
.
20. ![]() . Ответ.
. Ответ.![]() .
.
Приложение 1
Тематическое оценивание
«Модуль»
1вариант
1. Решите уравнения:
1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() ; 6)
; 6) ![]() .
.![]()
2. Решите неравенства:
1) ![]() ; 2)
; 2)![]() .
.
Тематическое оценивание
«Модуль»
2вариант
1. Решите уравнения:
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]() ;
;
5) ![]() ;
6)
;
6) ![]() .
. ![]()
2. Решите неравенства:
1) ![]() ;
2)
;
2)![]() .
.
Приложение 2
Проверочная работа
Модуль.
1 вариант
______________ ___________________________
Дата Фамилия, класс
1 уровень
1. Выберите правильное утверждение.
|
а |
б
|
в |
г
|
|
|
|
|
|
2. Раскройте знак модуля![]()
|
а |
б |
в |
г
|
|
|
|
0 |
|
3. Решите уравнение ![]() .
.
|
а |
б |
в |
г
|
|
|
2; |
корней нет |
2 |
4. Решите неравенство![]()
|
а |
б |
в |
г
|
|
решений нет |
|
|
|
2 уровень
5. Решите уравнение ![]() .
7. Решите неравенство
.
7. Решите неравенство![]() .
.
Ответ._____________ Ответ._____________
6. Решите уравнение ![]() . 8. Решите неравенство
. 8. Решите неравенство ![]() .
.
Ответ._____________ Ответ._____________
3 уровень
9. Решите уравнение![]() .
.
8. Решите неравенство ![]() .
.
Проверочная работа
Модуль.
2 вариант
______________ ___________________________
Дата Фамилия, класс
1 уровень
1. Выберите правильное утверждение.
|
а |
б
|
в |
г
|
|
|
|
|
|
2. Раскройте знак модуля![]()
|
а |
б |
в |
г
|
|
|
|
2 |
-2 |
3. Решите уравнение ![]() .
.
|
а |
б |
в |
г
|
|
-1,5 |
1,5; 6,5 |
-6,5 |
-1,5; -6,5
|
4. Решите неравенство![]()
|
а |
б |
в |
г
|
|
|
|
решений нет |
|
2 уровень
5. Решите уравнение![]() .
7. Решите неравенство
.
7. Решите неравенство![]() .
.
Ответ._____________ Ответ._____________
6. Решите уравнение![]() . 8. Решите неравенство
. 8. Решите неравенство ![]() .
.
Ответ._____________ Ответ._____________
3 уровень
9. Решите уравнение .
.
8. Решите неравенство ![]() .
.
Рекомендуемая литература:
1. Я.С.Фельдман, А.Я.Жаржевский. Математика. Решение задач с модулями. «Оракул», Санкт-Петербург, 1997.
2. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. Алгебраический тренажёр. «А.С.К.», Киев, 1997.
3. В.В.Вавилов, И.И.Мельников, С.Н.Олехник, П.И.Пасиченко. Задачи по математике. Уравнения и неравенства. «Наука», Москва, 1987.
4. Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.