Программа элективного курса

«Решение задач с параметрами»

(подготовка к ЕГЭ)

                        Пояснительная записка

Целью профильного обучения, как одного из направлений модернизации математического образования является обеспечение углубленного изучения предмета и подготовка учащихся к продолжению образования. Основным направлением модернизации математического школьного образования является отработка механизмов итоговой аттестации через введение единого государственного экзамена. Появление таких заданий на экзаменах далеко не случайно, т.к. с их помощью проверяется техника владения формулами элементарной математики, методами решения уравнений и неравенств, умение выстраивать логическую цепочку рассуждений, уровень логического мышления учащегося и их математической культуры. Решению задач с параметрами в школьной программе уделяется мало внимания. Большинство учащихся либо вовсе не справляются с такими задачами, либо приводят громоздкие выкладки. Причиной этого является отсутствие системы заданий по данной теме в школьных учебниках. В связи с этим возникла необходимость в разработке и проведении элективного курса для старшеклассников по теме: «Решение задач с параметрами». Многообразие задач с параметрами охватывает весь курс школьной математики. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления. Задачи с параметрами дают прекрасный материал для настоящей учебно-исследовательской работы.

                                   Цель курса

·         Формировать у учащихся умения и навыки по решению задач с параметрами для подготовки к ЕГЭ и к обучению в ВУЗе.

·         Изучение курса предполагает формирование у учащихся интереса к предмету, развитие их математических способностей.

·         Развивать исследовательскую и познавательную деятельность учащихся.

·         Обеспечить условия для самостоятельной творческой работы.

              В результате изучения курса учащийся должен:

• усвоить основные приемы и методы решения уравнений, неравенств, систем уравнений с параметрами;
• применять алгоритм решения уравнений, неравенств, содержащих параметр;
• проводить полное обоснование при решении задач с параметрами;
• овладеть исследовательской деятельностью.

Структура курса планирования учебного материала

Темы:

       I.            Первоначальные сведения. 2ч

    II.            Решения линейных уравнений, содержащих параметры. 2ч

 III.            Решения линейных неравенств, содержащих параметры. 2ч

IV.            Модуль и параметр. 2ч.

   V.            Квадратные уравнения и неравенства, содержащие параметры. 7ч

VI.            Свойства квадратичной функции в задачах с параметрами. 4ч

VII.            Рациональные уравнения.  2ч

VIII.            Рациональные неравенства. 2 ч

IX.            Иррациональные уравнения. 2ч  

   X.            Иррациональные неравенства. 2ч

XI.            Показательные и логарифмические уравнения, содержащие параметры.  4 ч 

XII.            Показательные и логарифмические неравенства, содержащие параметры . 4ч 

XIII.            Производная и ее применения. 4ч

XIV.            Тригонометрия и параметры. 4ч

XV.            Графические приемы решения. 4ч

XVI.            Нестандартные задачи с параметрами. 6ч

        §   количество решений уравнений;

        §   уравнения и неравенства с параметрами с некоторыми условиями.

XVII.            Текстовые задачи с использованием параметра. 4 ч

                               Краткое содержание курса

1.     Первоначальные сведения.

Определение параметра. Виды уравнений и неравенств, содержащие параметр.
Основные приемы решения задач с параметрам.
Решение простейших уравнений с параметрами.

Цель: Дать первоначальное представление учащемуся о параметре и помочь привыкнуть к параметру, к необычной форме ответов при решении уравнений.

II. Решение линейных уравнений (и уравнений, приводимых к линейным), содержащих параметр.

Общие подходы к решению линейных уравнений. Решение линейных уравнений, содержащих параметр.
Решение уравнений, приводимых к линейным.
Решение линейно-кусочных уравнений.
Применение алгоритма решения линейных уравнений, содержащих параметр.
Геометрическая интерпретация.
Решение систем уравнений.

Цель: Поиск решения линейных уравнений в общем виде; исследование количества корней в зависимости от значений параметра.

III. Решение линейных неравенств, содержащих параметр.

Определение линейного неравенства.
Алгоритм решения неравенств.
Решение стандартных линейных неравенств, простейших неравенств с параметрами.
Исследование полученного ответа.
Обработка результатов, полученных при решении.

Цель: Выработать навыки решения стандартных неравенств и приводимых к ним, углубленное изучение методов решения линейных неравенств.

IV. Модуль и параметр.

Определение модуля.

Алгоритм решения уравнений и неравенств с модулем.

Раскрытие разных модулей.

Графический способ решения.

Цель: Выработать навыки решения уравнений и неравенств с модулем, содержащих параметр.

V. Квадратные уравнения, содержащие параметр.

Актуализация знаний о квадратном уравнении. Исследования количества корней, в зависимости от дискриминанта. Использование теоремы Виета.

Исследование трехчлена.
Алгоритм решения уравнений.
Графический способ. Аналитический способ решения.
Классификация задач, с позиций применения к ним методов исследования.

Цель: Формировать умение и навыки решения квадратных уравнений с параметрами.

VI. Свойства квадратичной функции в задачах с параметрами.

Область значений функции. 
Область определения функции.
Монотонность. Координаты вершины параболы.

Цель: Познакомить с многообразием задач с параметрами, решаемых с помощью свойств  квадратичной функции.

VII. Рациональные уравнения. 

Общая схема решения целых и дробно-рациональных уравнений.

Решение соответствующих уравнений, содержащих параметр.

Различные способы решения.

Цель: Сформировать умение решать рациональные уравнения с параметром.

Исследование дробно-рациональных уравнений, содержащих параметр.

VIII. Рациональные неравенства.

Общая схема решения, «метод областей».

Различные способы решений.

Цель: Формировать умение и навыки решения рациональных неравенств с параметром.

IX.                        Иррациональные уравнения.

Схемы решения иррациональных уравнений.

Область определения уравнения.

Решение соответствующих уравнений, содержащих параметр.

Цель: Сформировать умение решать иррациональные уравнения с параметром.

Исследование иррациональных уравнений, содержащих параметр.

Х. Иррациональные неравенства.

Схемы решения иррациональных неравенств.

Решение соответствующих неравенств, содержащих параметр.

Цель: Формировать умение и навыки решения иррациональных неравенств с параметром.

XI. Показательные и логарифмические уравнения, содержащие параметры. 

Свойства степеней и показательной функции. Решение показательных уравнений, содержащих параметры.
Свойства логарифмов и логарифмической функции. Решение логарифмических уравнений с параметрами.

Цель: Сформировать умение решать показательные и логарифмические уравнения с параметрами.

XII. Показательные и логарифмические неравенства, содержащие параметры.

Свойства показательной функции. Решение показательных неравенств, содержащих параметры.
Свойства логарифмической функции. Решение логарифмических неравенств с параметрами.

Цель: Формировать умение и навыки решения показательных и логарифмических неравенств с параметром.

XIII. Производная и ее применения.

Касательная к функции.
Критические точки.
Монотонность.
Наибольшие и наименьшие значения функции.
Построение графиков функций.

Цель: Познакомить учащихся с типом задач с параметрами на применение методов дифференциального исчисления.

XIV. Тригонометрия и параметры.

Использование основных свойств тригонометрических функций в задачах с параметрами. Тригонометрические уравнения, содержащие параметр.
Тригонометрические неравенства, содержащие параметр.
Область значений тригонометрических функций.

Цель: Сформировать умение использования свойств тригонометрических функций при решении тригонометрических уравнений и неравенств с параметрами.

XV. Графические приемы решения.

Использование свойств различных функций при решении заданий с параметром.

Специфика решений графическим способом.

Преимущества и недостатки графического способа.

Цель: Научить графическим приемам решения задач с параметром.

XVI. Нестандартные задачи с параметрами.

Использование различных свойств при решении задач с параметрами.

Умение проводить анализ задачи, находить алгоритм решения.

Цель: Формировать навыки исследовательской деятельности, развивать логическое и математическое мышление.

XII. Текстовые задачи с использованием параметра.

Использование различных свойств при решении задач с параметрами.

Умение проводить анализ задачи, находить алгоритм решения.

Цель: Формировать навыки исследовательской деятельности, развивать логическое и математическое мышление.

Планирование   (64 часа)

Методические рекомендации  при изучении некоторых тем

                       Линейные и квадратные уравнения

Линейное уравнение, записанное в общем виде, можно рассматривать как уравнение с параметрами: ах = b, где х – неизвестное, а, b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Особым значением параметра а является значение а = 0. 

1. Если  а ≠ 0 , то  при  любой  паре  параметров  а   и  b  оно  имеет  единственное  решение  х = .

2. Если  а = 0, то  уравнение  принимает  вид: 0 х = b. В  этом  случае  значение  b = 0  является  особым  значением  параметра  b. 

2.1.    При  b ≠ 0 уравнение  решений  не  имеет.

2.2.    При  b = 0  уравнение  примет  вид: 0 х = 0. Решением  данного  уравнения  является  любое  действительное  число.

Пример.  Решить уравнение

2а(а — 2) х = а — 2.         (1)

Решение. Здесь контрольными будут те значения параметра, при которых коэффициент при х обращается в 0. Такими значениями являются а=0 и а=2. При этих значениях а невозможно деление обеих частей уравнения на коэффициент при х. В то же время при значениях параметра а≠0, а≠2 это деление возможно. Таким образом, целесообразно множество всех действительных значений параметра разбить на подмножества

A₁={0}, А₂={2} и А₃= {а≠0, а≠2}

и  решить уравнение (1) на каждом из этих подмножеств, т. е. решить уравнение (1) как семейство уравнений, получающихся из него при следующих значениях параметра:

1) а=0 ;    2) а=2 ;    3) а≠0, а≠2.

Рассмотрим эти случаи.

1) При а=0 уравнение (1) принимает вид 0 х = - 2. Это уравнение не имеет корней.

2) При а=2 уравнение (1) принимает вид 0 х=0. Корнем этого уравнения является любое действительное число.                                                                                   

3) При а≠0, а≠2  из уравнения (1) получаем, х =  ,

откуда х =  .

0твет:   1) Если а=0,то корней нет;

                     2)если а=2, то х – любое  действительное число;                                          

                     3)  если а≠0, а≠2 , то  х = .

Свойства квадратичной функции в задачах с параметрами

При решении различных задач часто используются не только свойства квадратного уравнения, но и свойства квадратичной функции. Полезно дать учащимся таблицу, позволяющую составлять систему неравенств для  нахождения решений задачи. Обратить внимание, что тогда  неравенства составляются в виде  аf(A)< 0 или аf(A)> 0 (а- старший коэффициент).

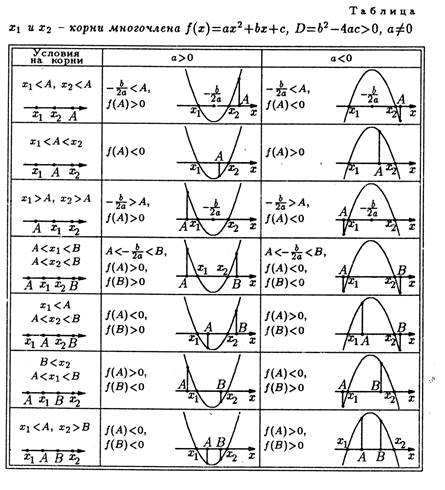Пример. При каких значениях параметра а один из корней уравнения

(а²-2)х²+(а²+а-1)х-а³+а=0

больше числа а, а другой меньше числа а?

Решение. Задача равносильна следующей: при каких значениях параметра а нули квадратичной функции

              g(х)= (а²-2)х²+(а²+а-1)х-а³+а

лежат на вещественной оси по разные стороны от точки х = а?

Исходя из таблицы, имеем условие: аf(A)< 0.

В нашем случае это условие принимает вид

(а²-2) g(а)<0.

Следовательно, требованию задачи удовлетворяют решения неравенства

(а²-2)((а²-2)а²+(а²+а-1)а-а³+а)<0, где а²-20 (а =, а =- требованию задачи не удовлетворяют).

Решая полученное неравенство,

находим, что а(-; -1)(1; ).

Ответ:     При  а(-; -1)(1; ).

                 Иррациональные уравнения с параметрами

       Существует несколько способов решения иррациональных уравнений с параметрами. Познакомимся с ними, разобрав следующий пример.

 Пример.          В зависимости от значений параметра  решить уравнение

(1)                                                                   

Решение. Решим уравнение (1) пятью способами, которые необходимо знать, ибо наряду с другими подходами они могут быть использованы и при решении иных типов уравнений.

1.Уравнение (1) равносильно системе

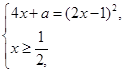
или системе

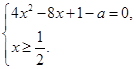(2)                                                                               

Решая уравнение из системы (2), находим

                                                                                         (3)

откуда следует, что при  уравнение (1) имеет одно решение . Если , то , и тогда уравнение (1) будет иметь два решения при тех значениях параметра , при которых совместна система

,

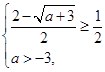т.е. при

Уравнение (1) будет иметь только один корень , если , а . В этом случае решая систему

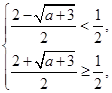
приходим к выводу, что .

Замечая теперь, что при  дискриминант уравнения системы (2) отрицателен, получаем

Ответ:    если , то решений нет;

                   если , то ;

                   если , то ;

                   если , то .

                                               Заключение

        Введение элективного курса «Решение задач с параметрами» необходимо учащимся в наше время как при подготовке к ЕГЭ, так и к вступительным экзаменам в ВУЗы. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики.

      Поэтому учащиеся, владеющие методами решения задач с параметрами, успешно справляются (и опыт это подтверждает) с другими задачами. Решение задач, уравнений с параметрами открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях и на любом другом математическом материале.

      При решении задач с параметрами одновременно активно реализуются основные методические принципы:

принцип параллельности – следует постоянно держать в поле зрения несколько тем, постепенно продвигаясь по ним вперед и вглубь;

принцип вариативности – рассматриваются различные приемы и методы решения с различных точек зрения: стандартность и оригинальность, объем вычислительной и исследовательской работы;

принцип самоконтроля – невозможность подстроиться под ответ вынуждает делать регулярный и систематический анализ своих ошибок и неудач;

принцип регулярности – увлеченные математикой дети с удовольствием дома индивидуально исследуют задачи, т. е. занятия математикой становятся регулярными, а не от случая к случаю на уроках. 

Разработанный элективный курс может быть использован учителями математики при подготовке к ЕГЭ, вступительным экзаменам в ВУЗы, на занятиях математического кружка.

Список литературы.

1.           Амелькин. В. В., Рабцевич В. Л.  Задачи с параметрами. Справочное пособие по      математике. – 2-е изд. - Мн. ООО «Асар», 2012. – 464 с.; ил.

2.           Галицкий М. Л. и др.  Сборник задач по алгебре для      учащихся шк. и кл. с углубл. изуч. математики. – 4-е изд. – Просвещение, 2007. – 271 с.; ил.

3.           Горнштейн П. И., Полонский В. Б., Якир М. С.  Задачи с параметрами. – 3-е изд. – М.; Илекса, Харьков: Гимназия, 2008, - 336 с.

4.           Дорофеев Г. В. и др.  Математика: Для поступающих в вузы: Пособие. – 5-е изд. – М.: Дрофа, 2010. – 672 с.; ил.

5.           Сканави М. И. и др. Сборник задач по математике для поступающих во втузы. – 7-е изд. – М. 1996. – 528 с.; ил.

27.             

Подбор задач с параметрами 7-11 классы.

7 класс

1. При каком значении  параметра  ,   является корнем уравнения   7?

Решение: Так как  корень уравнения 7 , то при подстановке    в уравнение получим верное равенство7  , откуда находим  .

Ответ:  при .

2. Решить уравнение     

1.         Если  , , то уравнение  примет следующий вид

   ,, это уравнение не имеет корней.

2.         Если ,                    

Ответ:  при , корней нет;

при   

3. Решить уравнение  относительно переменной  .

Решение:    Раскроем скобки:     

Запишем уравнение в стандартном виде: .     

В случае, если выражение а + 2 не нуль , т. е. если   , имеем решение

.

 Если  равно нулю, т.е., то имеем  равенство , поэтому

 – любое число.

Ответ: при         ;

при        - любое число.

4.Найдите значение коэффициента а в уравнении ах + 5у – 40 = 0, если известно, что решением уравнения является пара чисел:

а) (3; 2); б) (9; -1)

5. Найдите значение коэффициента b в уравнении 6х + bу – 35 = 0, если известно, что решением уравнения является пара чисел:

а) (0; 1); б) (3; 8,5)

6.  Найдите значение коэффициента с в уравнении 8х + 3у – с = 0, если известно, что решением уравнения является пара чисел: а) (2; -1); б) (3; 0)

7. При каком значении m решением уравнения mх + 4у – 12 m = 0 является пара чисел: а) (0; 3); б) (12; 0)

8.  Дана система уравнений х + ау = 35,bх + 2у = 27.Известно, что пара чисел (5; 6) является её решением, найдите значения а и b.

9.  При каком значении р график функции у = рх + 1 пройдёт через точку пересечения прямых 6х – у = 13 и 5х + у = 20 ?

10.  При каких значениях р график функции у = р² – 2рх проходит через точку (-1; 0) ?

8класс

1.  При каких значениях параметра а уравнение а(а + 3)х²+2(а + 3) – 3(а + 3) = 0

имеет более одного корня?

Решение.

Рассмотрим три случая.

1).   а  и   а-3

При таких значениях параметра а уравнение будет квадратным. Квадратное уравнение имеет более одного корня ( 2 различных ), когда дискриминант  Д>0.

Д = 4 ( а +3 )² + 12а ( а + 3 )² = 4 ( а + 3 )²( 1 + 3а ) >0.

Решая данное неравенство методом интервалов получаем ано так как а, то получаем, что а.

2).  а = 0.  Тогда данное уравнение принимает вид 6х – 9 = 0  и имеет только один корень, что не удовлетворяет условию задачи.

3).  а= -3. Получаем уравнение  0х²  + 0х + 0 = 0, которое имеет бесконечное множество решений, что удовлетворяет условию задачи.

  Ответ:   при а ; а = - 3.

2. При каких значениях a уравнение ax²—x+3=0 имеет единственное решение?

Решение.

Ошибочно считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй. Исходя из этого соображения, рассмотрим следующие случаи:

а) a=0. При этом уравнении принимает вид –x+3=0, откуда x=3, т.е. решение единственно.

б) a≠0, тогда ax²—x+3=0 – квадратное уравнение, дискриминант D=1-12a. для того, чтобы уравнение имело единственное решение, нужно чтобы D=0, откуда   

ответ:   или 

3. при каких значениях a уравнение (a-2)x²+(4-2a)x+3=0 имеет единственное решение?

Решение.

1)При a=2 исходное уравнение не имеет решения.

2) a≠2, тогда данное уравнение является квадратным и принимает вид

Искомые значения параметра- это корни дискриминанта, который обращается в нуль при         

Ответ: 

4.  Решить уравнение при всех значениях параметра.

c - 2 = x + 2 (Какое значение будет иметь корень уравнения при ?

Ответ: х = с - 4,

5.  Решить уравнение при всех значениях параметра.

x + 4 = a - 3 (Выяснить, при каких значениях параметра а корень уравнения равен -7)

Ответ: х = а - 7, х ≠ -7 ⇒ а ≠ 0.

6.  Решить уравнение при всех значениях параметра.

b - 8 + 2x = 2b (Выяснить, при каких значениях параметра корень уравнения не равен 4,5)

Ответ:

7.  При каких значениях параметра а уравнение (а² - 6а + 5) = а - 1 имеет

1) один корень;

2) ни одного корня;

3) бесконечно много корней?

Ответ: 1) а ≠ 1; а ≠ 5;

2) а = 5;

3) а = 1.

Решить уравнения при всех значениях параметра (№5 - 6).

8.  (2 - х)а = х + 1.

Ответ: а ≠ -1 ⇒x = (2a - 1)/(1+a).

9.  ( а² - 1)х = а + 1.

Ответ: а ≠ 1 ⇒ х = 1/(а - 1).

10*. |3x - c| = |x + 2|.

Ответ: с = -6 ⇒x = -2;c ≠ -6 ⇒x₁ = 0,5(c + 2), x₂ = 0,25(c - 2).

9 класс

1. Найдите все значения параметра а, при которых график функции

у=ах²+2х-а+2 пересекает ось Ох в одной точке.

Решение:1)Если а =0,то у=2х+2—линейная функции, графиком которой является прямая, пересекающая ось Ох в одной точке, т.к. к=2≠0

2)Если а≠0, то у=ах²+2х-а+2 - квадратичная функция, графиком которой является парабола, и пересекающая ось Ох в одной точке, если у_в=0

Итак, у_в= -(4-4а(-а+2))/4а, у_в=0

-(4+4а²-8а)/4а=0,

(4а²-8а+4)/4а=0

Т.к. а ≠ 0, то 4а²-8а+4=0,

а²-2а+1=0,

(а-1)²=0,

а=1.

2. Найдите все значения m, при которых парабола у=х²- х+1 имеет с прямой х + my - 1= 0 одну единственную общую точку.

Решение: Парабола и прямая имеют единственную общую точку, если система y=x²-x+1,x+my -1=0 имеет единственное решение.

Выясним, при каких m это возможно:

y=x²-x+1,

x+my-1=0;

x=1-my,

y=(1-my)²-(1-my)+1.

Преобразуем второе уравнение системы:

у=1-2my+m²y² - 1+my+1,

m²y² – (1+m)y+1=0.

Очевидно, что рассматриваемая система имеет единственное решение, если полученное квадратное уравнение имеет единственное решение.

Если m=0, то уравнение примет вид: у+1=0, которое имеет единственное решение и условие задачи выполняется.

Если m ≠ 0, то квадратное уравнение имеет 1 решение, если его D=0

D = (1+m)²- 4m²= 1+2m+m²- 4m²= 1+2m-3m²,

3m²- 2m -1 = 0

Ответ:  0; 1.

3. Найдите все значения а, при которых уравнение |3|x| - a²| =x – a имеет ровно три различных решения.    (Ответ: а=-3, а=-1)

4. Найдите все значения а, при каждом из которых уравнение ||x – a| - 2| =x+4 имеет бесконечное число корней.      (Ответ: а=-2, а=-6)

Найдите все значения k, при которых прямая y=kx пересекает график функции у= ||2x – 10|-4| в четырех различных точках.   (Ответ: 0<k<0,8)

5. Найдите все положительные значения k, при которых прямая y=kx пересекает в двух различных точках ломаную, заданную условиями:

                             1,   если |x|≤ 3

                  у=   -2x-5, если х<-3

                           2x-5, если x>3      

         (Ответ:  < k <2)

6.Найдите все значения m, при котором точки  А(-3;15), В(9;-5) и С(24;m) лежат на одной прямой.         (Ответ: m=-30)

7.  Найдите все значения а, при которых точка пересечения прямых у=2х+1 и у=а-5х находится в первой координатной четверти. (Ответ:а>1)

8.  Парабола у=х²+bx+c, симметричная относительно прямой х=-2, касается  прямой у= х+3. Найдите коэффициенты b, c.  (Ответ: b=4,c=4)

9.   При каких значениях а парабола у=3х²-2ах+4 и прямая у=а-2 не имеют общих точек?       (Ответ: -6<a<3)

10.  Постройте график функции y=f(x), где

                                    2x²+8x+8, если x<-1

                     f(x) =    |x|+1, если   -1≤x≤3

                                                , если  x>3.

 При каких значениях m прямая у=m имеет с графиком этой функции три общих точки.    (Ответ: m Î (0;1)∪(2;4))

10-11 класс 

            1.     При каких значениях a сумма квадратов корней уравнения больше чем 12? 
 Решение:     Дискриминант уравнения  равен 4a. Поэтому действительные корни этого уравнения существуют, если a і 0. Применяя к данному уравнению теорему Виета получаем x₁+x₂ = 2a и  . Отсюда  . Решениями неравенства  > 12, удовлетворяющими условию a і 0, являются числа a > 2. 
 Ответ: a > 2. 

2.  Для каждого значения параметра a определите количество решений уравнения |x²-7|x|+6| =а .

Решение:

Заметим, что количество решений уравнения

 |x²-7|x|+6| =а . 

 равно количеству точек пересечения графиков функций

y= |x²-7|x|+6|  и y = a.

График функции  y=x²-7x+6=(x)²-  показан на рис.1.

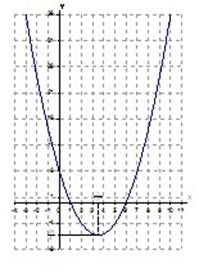
Рис.1

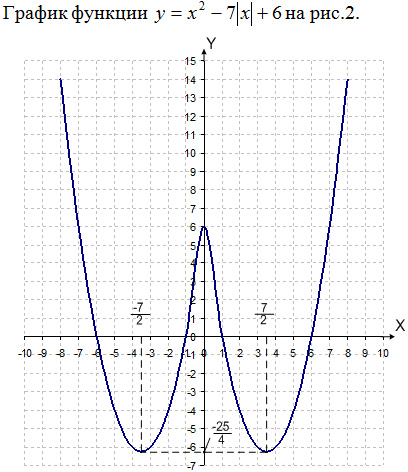
           Рис. 2

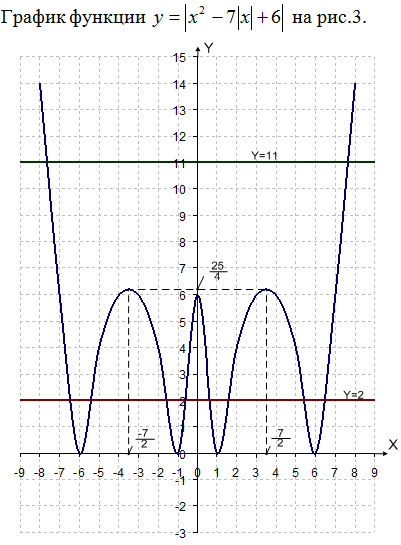
                                       Рис. 3

y = a – это горизонтальная прямая. По графику несложно установить количество точек пересечения в зависимости от a (например, при  a = 11 – две точки пересечения; при a = 2 – восемь точек пересечения).

Ответ: при a < 0 – решений нет; при a = 0 и a = 25/4  – четыре решения; при 0 < a < 6  – восемь решений; при a = 6 – семь решений; при

6 < a < 25/4 – шесть решений; при a > 25/4 – два решения.

Метод симметрии.  

 Довольно часто среди задач с параметрами встречаются такие, в которых требуется единственность решения. В ряде случаев необходимо обратить внимание на внешний вид условия задачи. Различного рода симметрии (симметрия областей значений, областей определения; симметрия относительно переменных) могут значительно упростить поиск искомых значений параметра.

Для решения задач данным методом можно воспользоваться следующим алгоритмом:

1.Изучить условие задачи.

2. Выполнить преобразования.

3. Решить задачу в данном виде.

3.Выбрать достаточное условие для даной задачи .

3. Найти все значения параметра b, при которых уравнение

  имеет единственное решение. [1]

Решение:

Уравнение не меняет своего вида при замене x на (−x) (ведь x ² и cos x это чётные функции).

 Уравнение  симметрично относительно преобразования x → (−x) (по другому относительно отражения в начале координат). Значит, данной симметрией будут обладать и решения данного уравнения. Если x₀ — корень уравнения  , то и число (−x₀) будет его корнем. Однако, условию задачи решение должно быть одно. Соответственно, корнем уравнения  является ноль. Если уравнение имеет ненулевое решение, то всего решений будет как минимум два.

Подставляя x = 0 в уравнение  , получаем

     .

Это — необходимое условие на b (только при таком b  уравнение может иметь нулевое решение).

 Является ли это условие достаточным; то есть, окажется ли при b = ctg 1 нулевое решение и в самом деле единственным, или же уравнение   будет иметь и другие корни помимо нуля.

 Для выяснения условия достаточности  значение b подставляется в уравнение :

Тангенс является возрастающей функцией на интервале (– ; ) . Косинус, являющийся аргументом тангенса, принимает значения из отрезка [−1; 1], а этот отрезок находится внутри интервала (– ; )

 Тогда, справедливо неравенство tg(cos (x)) <= tg 1, то есть при x = 0.

Итак,  при b = ctg 1 уравнение    имеет единственное (нулевое) решение. Ответ: b = ctg 1.

 Метод изменения ролей переменных.

Достаточно часто бывает необходимым поменять роли искомой переменной и одного из параметров, чтобы, по крайней мере, получить возможность проведения анализа представленного условия. Достаточно часто бывает, что степень искомой переменной гораздо выше, чем степень входящего в условие параметра. Изменение ролей в этом случае приводит к реальному упрощению процесса решения.

Для решения задач данным методом можно воспользоваться следующим алгоритмом:

1. Выполнить преобразования исходя из условия задачи.

3. Решить задачу в данном виде.

3.вернуться к первоначальному варианту и завершить решение.

4. Указать все значения параметра а , для которых уравнение имеет решение:   [4]

 =sinx

Sinx = t

│t│

 =t

│t│

Решение: Обозначим исходное уравнение равносильно системе

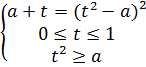
рассмотрим квадратное уравнение относительно параметра, найдём дискриминант данного уравнения :

    (2

   или

Последняя система равносильна

y= t²-t (  )[;0]

Ответ  

5. При каких значениях параметра  уравнение  имеет единственный корень?

Ответ:  )            .

6.  При каких значениях параметра  уравнение     имеет ровно три корня?

ответ:                 .

7. При каких  уравнение     имеет ровно три корня?

Ответ: .

8. Найдите все значения параметра , при каждом из которых система уравнений

имеет ровно два решения.

ответ: .

9. Найти все значения параметра , при которых система

имеет ровно два решения.

ответ: 

10. Найдите все значения , при каждом из которых уравнение  имеет два корня.

ответ: 

Скачано с www.znanio.ru