Министерство образования и науки Российской Федерации

Департамент образования Комитета по социальной политике и культуре администрации города Иркутска

Муниципальное бюджетное общеобразовательное учреждение 

Лицей №1

 

 

 

 

 

 

 

ПРОГРАММА ФАКУЛЬТАТИВНОГО КУРСА 

 

ДОПОЛНИТЕЛЬНЫЕ МЕТОДЫ  РЕШЕНИЯ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ

 

для обучающихся 9 класса

 

 

образовательная область математика

 

 

 

 

 

 

 

 

 

Составил: Руднева Н.Н.

учитель математики МБОУ г. Иркутска Лицей № 1

 

 

 

 

Иркутск, 2019  

Оглавление

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА ............................................................................................................ 3

ПЛАНИРУЕМЫЕ ОБРАЗОВАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ ............................................................. 4

СОДЕРЖАНИЕ ПРОГРАММЫ ............................................................................................................ 6

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ................................................................................................ 8

СИСТЕМА ОЦЕНИВАНИЯ ПЛАНИРУЕМЫХ РЕЗУЛЬТАТОВ И УУД ОБУЧАЮЩИХСЯ

 ..................................................................................................................................................................... 12

ОПИСАНИЕ ПРИМЕНЯЕМЫХ ВИДОВ ДЕЯТЕЛЬНОСТИ ....................................................... 13

СПИСОК ЛИТЕРАТУРЫ ..................................................................................................................... 15

ИНТЕРНЕТ РЕСУРСЫ ......................................................................................................................... 15

Приложение 1 ........................................................................................................................................... 16

Зачетные работы по содержанию факультативного курса ............................................................. 16

Приложение 2 ........................................................................................................................................... 20

Промежуточное тестирование по теме «Опорные факты, связанные с равновеликостью и

отношением площадей» ......................................................................................................................... 20 Приложение 3 ........................................................................................................................................... 24

Методическая разработка занятия ...................................................................................................... 24

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

 

Нормативные документы, обеспечивающие реализацию программы:

Федеральный закон от 29 декабря 2012 № 273-ФЗ «Об образовании в Российской Федерации». 

Концепция развития математического образования в Российской Федерации (утв. распоряжением Правительства РФ от 24 декабря 2013 г. N 2506-р).

Федеральный государственный образовательный стандарт Основного общего образования (утв. приказом Министерства образования и науки Российской Федерации от 17 декабря 2010 г. № 1897).

 

Изучение геометрии в 7-9 классах имеет ряд особенностей: обучающимся необходимо запоминать много фактов, требующих аккуратности в формулировках; осваивать математический язык и символику; выполнять чертежи к задачам; осуществлять умозаключения по определённым правилам; оформлять решение задач, опираясь на лаконичные пояснения и грамотные ссылки на определения и теоремы. Исходя из сущности геометрических задач, обучение их решению – это обобщение и систематизация учебного опыта учащихся. Одним из средств целенаправленной организации этого процесса является планомерное знакомство обучающихся с системой методов решения задач. Зная разновидности методов, их названия, специфику использования, отличительные особенности, имея зрительные ассоциации по конкретным конфигурациям, школьник на этапе поиска решения задачи будет осуществлять не хаотичный, а осознанный поиск походящего решения. Это позволит отказаться от стихийности учебной деятельности ученика и перейти к её целенаправленной организации и планомерному формированию.

 Основная функция факультативного курса по геометрии – формирование представлений об идеях и методах решения геометрических задач; развитие творческих способностей у школьников, осознанных мотивов учения.

Решение геометрических задач вызывает трудности у многих учащихся. Это объясняется, прежде всего, тем, что редко какая-либо задача по геометрии может быть решена с использованием определённой теоремы или формулы. Большинство задач требует применения разнообразных теоретических знаний, доказательства утверждений, справедливых лишь при определенном расположении фигуры, применение различных формул. Приобрести навык в решении задач можно, лишь решив достаточно большое их количество, ознакомившись с различными методами, приёмами и подходами.

Программа для общеобразовательных школ по геометрии не акцентирует внимание на методах решения задач, особенно на их частные случаи.

Искусство же решать задачи основывается на хорошем знании теоретической части курса, знании достаточного количества геометрических фактов, в овладении определённым арсеналом приёмов и методов решения геометрических задач.

Методы решения геометрических задач обладают некоторыми особенностями, а именно: большое разнообразие, трудность формального описания, взаимозаменяемость, отсутствие чётких границ области применения.

Поэтому целесообразно рассмотреть применение подходов, приёмов, методов при решении конкретных задач.

Знакомство учащихся с методами решения геометрических задач стимулирует анализ учащихся своей деятельности по решению задач, выделению в них общих подходов и методов, их теоретическое осмысление и обоснование, решение заданий несколькими способами. Особое внимание уделяется аналитическому способу решения задач, доводится до понимания учащихся, что анализ условия задачи, анализ решения задачи – важнейшие этапы её решения. 

Знание методов решения геометрических задач позволяет решать, казалось бы, сложные математические задачи просто, понятно и красиво.

Кроме того, предлагаемый курс позволяет создать целостное представление о теме и значительно расширить спектр задач, благодаря пониманию методов, приёмов решения задач.

Цель курса: 

Расширение и систематизация знаний о математических идеях, методах и приёмах решения планиметрических задач.

Задачи курса:

Общеобразовательные: 

Формировать навыки решения задач с использованием различных математических методов, в том числе задач на доказательство:

•      алгебраического метода;

•      метода дополнительного построения;

•      метода вспомогательной окружности;

•      метода площадей;

•      метода геометрических преобразований.

Формировать умение определять и отбирать (комбинировать) методы при решении задач, навыки решения задач на комбинацию геометрических фигур (треугольник, четырехугольник, окружность).

Развивающие:

•      Развитие познавательного интереса;

•      Развитие        логического   мышления,    наблюдательности,   воображения, математической интуиции, математической речи;

•      Развитие умственных способностей: гибкости, критичности и глубины ума, самостоятельности и широты мышления, памяти, способности к цельности восприятия, генерированию идей, укрупнению информации.

•      Формирование исследовательских навыков применения методов научного познания: анализа и синтеза, абстрагирования, обобщения и конкретизации, индукции и дедукции, классификации, аналогии и моделирования.

•      Развитие общих учебных умений: постановки учебной цели, выбора средств ее достижения, структурирования информации, выделения главного.

Воспитательные:

•      Формирование представлений о математике как части общечеловеческой культуры, о роли математики и ее методов в общественном прогрессе.

•      Развитие и углубление познавательного интереса к геометрии, стимулирование самостоятельности учащихся в изучении теоретического материала, создание ситуаций успеха по преодолению трудностей.

•      Стимулирование исследовательской деятельности учащихся.

•      Воспитание нравственных качеств личности: настойчивости, целеустремленности, творческой активности и самостоятельности, критичности мышления, способности к аргументированному отстаиванию своих взглядов и убеждений. Место факультативного курса в учебном плане

На изучение факультативного курса отводится 1 час в неделю в 9 классе в течение учебного года, всего – 34 часа. 

ПЛАНИРУЕМЫЕ ОБРАЗОВАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ

 Факультативный курс направлен на развитие у обучающихся пространственного геометрического воображения и зоркости, логического мышления, способностей позволяющих моделировать проблемную ситуацию и находить варианты её разрешения; на формирование умения применять систему знаний по геометрии в жизненных ситуациях.  Факультативный курс направлен на формирование:

Личностных результатов: ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры; распознавать логически некорректные высказывания, отличать гипотезу от факта; контролировать процесс и результат учебной математической деятельности.

Метапредметных результатов: 

•      Умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и

познавательных задач;

•      Умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;

•      Умение адекватно описывать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;

•      Осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовитых связей;

•      Умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;

•      Умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;

•      Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;

•      Умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;

•      Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимать сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;

•      Умение самостоятельно ставить цели, выбирать и создавать алгоритм для решения учебных математических проблем.

 Предметных результатов:

•      Овладение базовым понятийным аппаратом по основным разделам содержания.

•      Умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символически, логические обоснования доказательства математических утверждений;

•      Овладение навыками устных, письменных, инструментальных вычислений при решении планиметрических задач.

•      Умение применять систематические знания о плоских геометрических фигурах и их свойствах для решения геометрических задач.

•      Умение применять изученные идеи и методы для решения планиметрических задач повышенной трудности, практического характера.

•      Умение работать в информационном поле (таблицы, схемы, диаграммы, графики, последовательности, цепочки, совокупности).

•      Умение представлять, анализировать и интерпретировать условие и требование планиметрических задач, выводить следствий из требования и условия задачи, выполнять запись решения задачи (доказательства задачи – теоремы).

 

СОДЕРЖАНИЕ ПРОГРАММЫ

 

1.  МЕТОДЫ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ (2 ЧАСА)

Цель: Создание условия для формирования навыков и умений по организации поиска метода решения планиметрических задач, используя анализ условия задачи, выделении этапов решения задач и содержания каждого этапа, оформлению решения задачи с обоснованием шагов решения.

 

Три основных метода решения геометрических задач: геометрический; алгебраический; комбинированный. Геометрические методы решения задач. Анализ условия задачи, анализ решения задачи – этапы решения задачи. 

 

2. АЛГЕБРАИЧЕСКИЙ МЕТОД РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ (3 ЧАСА)

Цель: Создание условий для усвоения обучающимися сути алгебраического метода решения геометрических задач: искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнения (системы уравнений).

 

Метод прямого счета или поэтапно-вычислительный метод. Метод геометрических мест. Метод составления уравнений или систем уравнений. Метод применения тригонометрии к решению геометрических задач.  Решение планиметрических задач алгебраическим методом.

 

3. МЕТОД ПЛОЩАДЕЙ (6 ЧАСОВ)

 

Цель: Создание условия для усвоения обучающимися сути метода площадей, заключающегося в составлении и сравнении различных выражений для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, решая которое находят значение неизвестной переменной. 

Опорные факты, связанные с равновеликостью многоугольников и отношением площадей. Метод перекраивания фигуры в равновеликую ей фигуру. Метод сравнения площадей фигур. Метод перегруппировки площадей. Метод перекрывающихся площадей.  Отношение площадей.

 

4. МЕТОД ДОПОЛНИТЕЛЬНЫХ ПОСТРОЕНИЙ (10 ЧАСОВ)  

Цель: Создание условий для усвоения обучающимися сути метода дополнительных построений, заключающейся в том, что чертеж к задаче, на котором трудно заметить связи между данными и искомыми величинами, дополняется новыми (вспомогательными) элементами, после чего эти связи становятся более ощутимыми или даже очевидными.

Роль чертежа при поиске решения планиметрических задач. Дополнительные построения, связанные с данной фигурой. Дополнительные построения определённого вида при решении конкретных геометрических задач. Типовые конфигурации для выбора дополнительного построения: разбиение  и дополнение. Решение задач, требующих дополнительные построения. Признаки принадлежности четырех точек окружности (задача-теорема). Метод вспомогательной окружности.

5. МЕТОД ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ (7 ЧАСОВ)

 

Цель: Создание условий для усвоения обучающимися сути метода геометрических преобразований, где кроме данных в условии задачи фигур, рассматриваются  вспомогательные фигуры, полученные из данных фигур или их элементов при помощи какого-либо частного вида преобразования (осевой симметрии, параллельного переноса, гомотетии и др.). 

 

Метод осевой симметрии.  Метод параллельного переноса. Метод поворота.  Метод центральной симметрии.  Метод подобия. Теорема Менелая. Теорема Чевы. Метод вспомогательных фигур, полученных с помощью «спрямления».

 

6. КОМБИНИРОВАННЫЕ МЕТОДЫ РЕШЕНИЙ (6 ЧАСА)

 

Цель: Создание условий для развития навыков решения планиметрических задач комбинированием алгебраического и геометрических методов решения, систематизировать знания учащихся по геометрическим методам решения задач.

 

Решение задач комбинированным методом на нахождение линейных элементов многоугольников и окружностей. Решение комбинированным методом на нахождение площадей геометрических фигур.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ 

ПО ФАКУЛЬТАТИВНОМУ КУРСУ

«ДОПОЛНИТЕЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ»

9 класс, 34 часа (1 час в неделю) 

 

№пп	Тема	Колво часов	Вид деятельности	Планируемые результаты (обучающиеся научатся)
				Предметные	Познавательные УУД	Коммуникативные УУД	Регулятивные УУД
1	Методы решения геометрических задач	2	Составление опорного конспекта. Планирование хода решения задачи. Пошаговый контроль правильности и полноты выполнения плана решения задачи.	Систематизировать знания об основных методах решения геометрических задач. Осуществлять построение модели условия задачи в виде чертежа или уравнения. Осуществлять способ поиска решения задачи, используя анализ условия задачи, выделять этапы решения задачи и содержание каждого этапа. Оформлять решение задачи опираясь на лаконичные пояснения и грамотные ссылки на определения и теоремы. Обучающийся получит возможность научиться:  Анализировать затруднения при решении задач.	Структурировать знания, устанавливать причинноследственные связи, строить логическое рассуждение. Использовать математические средства наглядности для иллюстрации, интерпретации, аргументации.	Формулировать собственное мнение, аргументировать его, владея приёмами монологической и диалогической речи. Владеть письменной речью в соответствии с нормами русского языка.	Адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.
2	Алгебраический метод решения геометрических задач	3	Составление опорного конспекта. Построение модели (рисунки, чертежи, выкладки, математические записи) по условию задачи. Планирование хода решения задачи. Пошаговый контроль правильности и полноты выполнения плана решения задачи. Поиск, обнаружение и устранение ошибок логического (в	Осознавать            выбор алгебраического   метода решения                 планиметрических задач.  Геометрически интерпретировать формулы и приёмы вычислений, перенося их на фигуры. Рационально         применять формулы в процессе решения задач. Применять алгебраический метод при решении задач на вычисление площадей	Владеть логическими действиями: анализ, синтез, обобщение, аналогии. Создавать модели решения учебных и познавательных задач. Использовать математические средства наглядности для иллюстрации, интерпретации, аргументации.	Находить общее решение задачи и разрешать конфликты на основе согласования позиций и учета интересов участников конфликта.	Определять последовательность действий, способов и средств решения, в том числе альтернативных, учебных и познавательных задач, выбирать наиболее эффективные способы решения. Осуществлять контроль своей деятельности в процессе достижения результата

 

			ходе решения) и арифметического (в вычислении) характера. Сравнение разных способов решения задачи, выбор удобного способа.	многоугольников. Обучающийся получит возможность научиться:  Выбирать оптимальный метод решения задачи и осознавать выбор метода. Решать задачи алгебраическим методом                решения планиметрических                 задач, применять его в новых по сравнению             с                 изученными ситуациях.
3	Метод площадей	6	Составление опорного конспекта. Построение модели (рисунки, чертежи, выкладки, математические записи) по условию задачи. Планирование хода решения задачи. Пошаговый контроль правильности и полноты выполнения плана решения задачи. Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера. Сравнение разных способов решения задачи, выбор удобного способа. Накопление и использование опыта решения планиметрических задач.	Решать задачи на вычисление площади фигур, используя приёмы перекраивания, перегруппировки, сравнения, отношения площадей, основанные на понятии равновеликости и равносоставленности. Обучающийся получит возможность научиться:  Выбирать оптимальный метод решения задачи, находить разные решения задачи, если возможно. Решать задачи геометрическим методом решения планиметрических задач: метод площадей, применять его в новых по сравнению с изученными ситуациях.	Владеть логическими действиями: анализ, синтез, обобщение, аналогии. Устанавливать причинноследственные связи, использовать их для объяснения свойств. Создавать модели решения учебных и познавательных задач. Использовать математические средства наглядности для иллюстрации, интерпретации, аргументации.	Находить общее решение задачи и разрешать конфликты на основе согласования позиций и учета интересов участников конфликта.  Ясно, точно, грамотно излагать свои мысли в письменной речи.	Выделять и осознавать то, что уже усвоено и что еще подлежит усвоению, осознавать качество и уровень усвоения. Определять последовательность действий, способов и средств решения, в том числе альтернативных, учебных и познавательных задач, выбирать наиболее эффективные способы решения. Осуществлять контроль своей деятельности в процессе достижения результата
4	Метод дополнительных построений	10	Составление опорного конспекта. Построение модели (рисунки, чертежи, выкладки, математические записи) по условию задачи. Планирование хода решения задачи. Пошаговый контроль	Выполнять чертёж к задаче, максимально соответствующий условию. Применять типовые конфигурации для выбора дополнительного построения. Извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах и их	Осознанно владеть логическими действиями определения понятий, обобщения, установления аналогий. Проводить сравнение, классификацию по заданным критериям. Использовать математические средства	Находить общее решение задачи и разрешать конфликты на основе согласования позиций и учета интересов участников конфликта.  Распознавать логически некорректные высказывания	Выделять и осознавать то, что уже усвоено и что еще подлежит усвоению, осознавать качество и уровень усвоения. Определять последовательность действий, способов и средств решения, в том

 

			правильности и полноты выполнения плана решения задачи. Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера. Сравнение разных способов решения задачи, выбор удобного способа. Накопление и использование опыта решения планиметрических задач.	свойствах, для осознанного выбора типа дополнительного построения.  Решать задачи, требующие дополнительных построений, в том числе вспомогательной окружности. Обучающийся получит возможность научиться:  Выбирать оптимальное дополнительное построение при решении задач, рассматривать возможности различных дополнительных построений в определенных конфигурациях, находить разные решения задачи, если возможно. Решать задачи геометрическим методом решения планиметрических задач: метод дополнительных построений, применять его в новых по сравнению с изученными ситуациях.	наглядности для иллюстрации, интерпретации, аргументации. Создавать модели для решения учебных и познавательных задач.		числе альтернативных, учебных и познавательных задач, выбирать наиболее эффективные способы решения. Осуществлять контроль и корректирование своей деятельности в процессе достижения результата.
5	Метод геометрических преобразований	7	Построение модели (рисунки, чертежи, выкладки, математические записи) по условию задачи. Планирование хода решения задачи. Пошаговый контроль правильности и полноты выполнения плана решения задачи. Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера. Сравнение разных способов решения задачи, выбор удобного способа. Накопление и	Владеть приёмами построения фигур с использованием движений и преобразования подобия. Применять свойства движения и подобия для обоснования свойств фигур, при решении задач методом геометрических преобразований.  Применять идеи движения и подобия при решении задач на вычисление площадей многоугольников. Обучающийся получит возможность научиться:  Решать задачи геометрическим методом решения планиметрических задач: метод геометрических преобразований, применять его в новых по сравнению с	Осознанно владеть логическими действиями определения понятий, анализа. Устанавливать причинноследственные связи, строить логические рассуждения. Создавать модели для решения учебных и познавательных задач.	Слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие и сотрудничество со сверстниками и учителем. Ясно, точно, грамотно излагать свои мысли в письменной речи.	Адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.  Определять последовательность действий, способов и средств решения учебных и познавательных задач, выбирать наиболее эффективные способы решения. Осуществлять контроль своей деятельности в процессе достижения результата.

 

			использование опыта решения планиметрических задач.	изученными ситуациях. В             повседневной                 жизни: выделять                 характеристики рассматриваемой                в                 задаче ситуации,                 отличные               от реальных                (те, от                 которых абстрагировались), конструировать новые ситуации с учетом этих характеристик.
6	Комбинация методов	6	Поиск необходимой теоретической информации в учебной и в справочной литературе. Построение модели (рисунки, чертежи, выкладки, математические записи) по условию задачи. Планирование хода решения задачи. Пошаговый контроль правильности и полноты выполнения плана решения задачи. Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера. Сравнение разных способов решения задачи, выбор удобного способа. Накопление и использование опыта решения планиметрических задач.	Осознавать выбор геометрического и алгебраического метода решения планиметрических задач.  Геометрически интерпретировать формулы и приёмы вычислений, перенося их на фигуры. Рационально         применять формулы в процессе решения задач. Применять                 комбинированный метод при решении задач на вычисление           площадей многоугольников. Обучающийся получит возможность научиться:  Проводить доказательство, выполнять опровержение, используя изученные методы,; Выбирать изученные методы и их комбинации для решения математических задач.	Выполнять анализ заданий с большей долей самостоятельности. Самостоятельно конструировать новый способ действия.	Организация и планирование учебного сотрудничества с учителем и сверстниками. Представлять конкретное содержание и сообщать его в письменной и устной форме. Вступать в диалог, участвовать в коллективном обсуждении проблем, владеть монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка	Определять последовательность действий, способов и средств решения, в том числе альтернативных, учебных и познавательных задач, выбирать наиболее эффективные способы решения. Осуществлять контроль и корректирование своей деятельности в процессе достижения результата.

СИСТЕМА ОЦЕНИВАНИЯ ПЛАНИРУЕМЫХ РЕЗУЛЬТАТОВ И УУД ОБУЧАЮЩИХСЯ

 

Система оценки предметных результатов освоения программы факультативного курса осуществляется с учётом уровневого подхода: предполагается выделение базового уровня достижений как точки отсчёта при построении всей системы оценки и организации индивидуальной работы с обучающимися. Реальные достижения обучающихся могут соответствовать базовому уровню, а могут отличаться от него как в сторону превышения, так и в сторону недостижения.

Достижения обучающихся предметных результатов распределяются по уровням:

Необходимый уровень (базовый) – решение типовой задачи, подобной тем, что решали уже много раз, где требовались отработанные действия (раздел «Обучающийся научится» программы курса) и усвоенные знания, входящие в опорную систему знаний курса. Это достаточно для продолжения образования, это возможно и необходимо всем. Качественные оценки «хорошо, но не отлично» или «нормально» (решение задачи с недочётами). 

Повышенный уровень (программный) – решение нестандартной задачи, где потребовалось: либо действие в новой, непривычной ситуации (в том числе действия из раздела «Обучающийся получит возможность научиться» программы курса); либо использование новых, усваиваемых в данный момент знаний, в том числе выходящих за рамки опорной системы знаний по курсу.  Умение действовать в нестандартной ситуации – это отличие от необходимого уровня. Качественные оценки: «отлично» или «почти отлично» (решение задачи с недочётами). 

Максимальный уровень (необязательный) – решение не изучавшейся в классе «сверхзадачи», для которой потребовались либо самостоятельно добытые, не изучавшиеся знания, либо новые, самостоятельно усвоенные умения и действия, требуемые на следующих ступенях образования. Это демонстрирует исключительные успехи отдельных учеников по отдельным темам сверх программы курса.  Качественная оценка «превосходно». 

 

Уровни успешности

  

Не достигнут необходимый уровень   Не решена типовая, много раз отработанная задача

Необходимый (базовый) уровень   Решение типовой задачи, подобной тем, что решали уже много раз, где требовались отработанные умения и уже усвоенные знания

Повышенный (программный) уровень   Решение нестандартной задачи, где потребовалось либо применить новые знаний по изучаемой в данный момент теме, либо уже усвоенные знания и умения, но в новой, непривычной ситуации

Максимальный (необязательный) уровень   Решение задачи по материалу, не изучавшемуся в классе, где потребовались либо самостоятельно добытые новые знания, либо новые, самостоятельно усвоенные умения

Пониженный уровень достижений свидетельствует об отсутствии систематической базовой подготовки, о том, что обучающимся не освоено даже и половины планируемых результатов, которые осваивает большинство обучающихся, о том, что имеются значительные пробелы в знаниях, дальнейшее обучение затруднено. Данная группа обучающихся требует специальной диагностики затруднений в обучении, пробелов в системе знаний и оказании целенаправленной помощи в достижении базового уровня. После изучения данного курса учащиеся должны:

Учащиеся должны знать / понимать:

-                     значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

-                     универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности.

Учащиеся должны уметь:

•       точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе решения заданий;

•       правильно анализировать условие задачи;

•       выполнять грамотный чертеж к задаче;

•       осознанно выбирать метод решения планиметрической задачи;

•       в сложных задачах использовать вспомогательные задачи (задачи - спутники);

•       логически обосновывать собственное мнение;

•       использовать символический язык для записи решений геометрических задач; • следить за мыслью собеседника; корректно вести дискуссию.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

-                     исследования (моделирования) несложных практических ситуаций на основе изученных моделей;

-вычисления площадей геометрических фигур при решении практических задач, используя при необходимости справочники и вычислительные устройства.

Достижение обучающимися личностных результатов описываются готовностью и способностью обучающихся к саморазвитию, сформированностью мотивации к обучению и познанию.

Достижение обучающимися метапредметных результатов описываются освоенными обучающимися универсальными учебными действиями (познавательные, регулятивные и коммуникативные), обеспечивающими овладение ключевыми компетенциями, составляющими основу умения учиться, и межпредметными понятиями. 

 

ОПИСАНИЕ ПРИМЕНЯЕМЫХ ВИДОВ ДЕЯТЕЛЬНОСТИ

 

№ п/п	Вид деятельности	Действия учителя	Действия учащихся
1	Составление опорного конспекта.	Проводит объяснение учебного материала, записывает на доске опорные слова. Стимулирует самообразовательную деятельность учащихся. Обучает учащихся осознанно сворачивать информацию, составлять опорный конспект.	Упорядочивает свои знания, классифицирует, систематизирует, структурирует, выявляет существенное. Фиксирует объяснение нового материала в виде опорного конспекта.
2	Поиск необходимой теоретической информации в учебной и в справочной литературе.	Предлагает задания, для выполнения которых необходимо использовать альтернативные источники информации – дополнительную литературу, компьютерные базы данных, Интернет и т. д. Поощряет учащихся к использованию дополнительной информации. Обучает учащихся осознанно сворачивать информацию, составлять план, конспект и т. д. Стимулирует критически оценивать информацию.	Получает информацию из разных источников: учебной, справочной, научнопопулярной, компьютерных баз данных и Интернета. Объединяет различные источники информации. Выделяет необходимый массив информации – сворачивает информацию, используя опорные слова составляет план, конспект и т. д. Упорядочивает свои знания. Критически оценивает информацию.
3	Построение              модели	Ставит (обсуждает с учащимися)	Соотносит теоретические знания с
	(рисунки,                чертежи, выкладки, математические записи) по условию задачи.	учебные задачи, организует беседу, дает, при необходимости, образец записи, стимулирует самостоятельность и активность учащихся при построении рисунков и чертежей, математических выкладок.	практикой. Высказывает собственное мнение и презентует свой рисунок или чертеж к задаче. Умеет аргументированно доказывать свое высказывание. Оценивает свой ответ.
4	Планирование       хода решения задачи.	Стимулирует творчество учащихся. Предлагает задания разного уровня, вариативные домашние задания. Организует фронтальную и парную работу. Создает проблемные ситуации. Побуждает высказывать собственное мнение. Стимулирует предоставлять аргументированные ответы.  Консультирует учащихся по «раскрытию термина понятия» (выделению существенных признаков понятия), выведению следствий из условия задачи, выведению следствий из требований задачи.  Обучает правильно задавать вопросы и отвечать на них. Рекомендует самооценивание и взаимооценивание.	Устанавливает несоответствие между условиями новой учебной задачи и известными способами действий, определяет способ выполнения учебной задачи. Осознанно выбирает уровень тематической работы, уровень домашней работы. Работает фронтально и в паре. Выявляет способ решения (прием работы). Устанавливает причинно-следственные связи, ищет способ решения задачи, решения проблемы. Высказывает собственное мнение, аргументированно его доказывает. Оценивает свой ответ. Определяет цели своей деятельности, ставит личностно значимые цели. Оценивает отдельные операции и результаты учебной деятельности, дает прогностическую оценку своих возможностей относительно решения поставленной перед ним учебной задачи.
5	Пошаговый контроль правильности и полноты выполнения плана решения задачи.	Используя диалоговые методы, организует обсуждение с учащимися плана решения задачи. Побуждает высказывать собственное мнение. Стимулирует предоставлять аргументированные ответы.  Фиксирует результат мысленного построения цепи рассуждений при доказательстве, решении задач. При необходимости оказывает учащимся помощь в обобщении результатов.	Выделяет в каждом шаге доказательства (решения) промежуточное условие, промежуточный вывод, обоснование. Работает в паре и выполняет пошаговую запись доказательства (решения) в соответствии с планом доказательства.  Обобщает способ решения на определенный класс задач.
6	Поиск, обнаружение и устранение ошибок логического (в ходе решения)               и арифметического (в вычислении) характера.	Предоставляет возможность учащимся самостоятельно с помощью других учащихся сравнивать полученный результат с эталоном.	Находит и исправляет допущенные ошибки, осмысливает их причины.
7	Сравнение разных способов решения задачи, выбор удобного способа.	Побуждает к поиску альтернативных решений, направляет учебную (поисковую) деятельность учащихся, контролирует ход поиска, даёт оценку.	Работает в паре. Сравнивает, устанавливание частное или действует по известному образцу (по аналогии) при выполнении типовых заданий, формулирует гипотезы, ищет другие способы решения, исследует, классифицируют задачи по методам решения задачи, самостоятельно составляют новую модель, для решения задачи другим способом.
8	Накопление и использование опыта решения планиметрических задач.	Предлагает дифференцированные по уровню трудности задания, для выполнения которых необходимо привлечение собственного опыта решения задач.	Устанавливают несоответствие между условиями новой учебной задачи и известными способами, и методами решения геометрических задач. Самостоятельно генерирует идеи, применяет свои знания для решения задач в новой ситуации, задач практической направленности. Решает задачу аналитическими методами, выбирает метод решения задачи; конкретизирует и обобщает задачу, использует аналогию.

 

 

 

СПИСОК ЛИТЕРАТУРЫ

Боженкова Л.И. Методика формирования универсальных учебных действий при обучении геометрии / Л.И. Боженкова. – 2- е изд. – М. : БИНОМ. Лаборатория знаний, 2015ю – 205 с. : ил.

Гордин Р.К., Геометрия. Планиметрия. 7-9 классы. – 3-е изд., испр. – М.: МЦНМО, 2006. – 416 с: ил.

Полонский В.Б., Рабинович Е.М., Якир М.С. Учимся решать задачи по геометрии. Учеб.метод. пособие. – К.: «Магистр – S», 1996. – 256 с.

Рогановский, Н.М. Геометрия. 9 класс. Многообразие идей и методов: пособие для учащихся / Н.М. Рогановский, Е.Н. Рогановская, О.И. Тавгень. – Минск: Аверсэв, 2011. – 144 с.: ил. – (Факультативные занятия)

 Рогановский, Н.М. Геометрия. 7 – 9 классы. Многообразие идей и методов: пособие для учителей / Н.М. Рогановский, Е.Н. Рогановская, О.И. Тавгень. – Минск: Аверсэв, 2011. – 313 с.: ил. – (Факультативные занятия)

Смирнова, Е.С. Планиметрия: виды задач и методы их решений: Элективный курс для учащихся 9 – 11 классов. Электронное издание. М.: МЦНМО, 2017. – 416 с.

 

 

ИНТЕРНЕТ РЕСУРСЫ

 

Воистинова Г. Х., Кулаков А. П. Обучение учащихся использованию дополнительных построений в геометрических задачах [Текст] // Педагогическое мастерство: материалы V Междунар. науч. конф. (г. Москва, ноябрь 2014 г.). — М.: Буки-Веди, 2014. — С. 68-71. — URL https://moluch.ru/conf/ped/archive/144/6587/ (дата обращения: 06.06.2019).

https://shkolkovo.net/catalog/zadachi_po_planimetrii/trebuyuschie_dopolnitelnogo_postroeniya https://shkolkovo.net/catalog/zadachi_po_planimetrii/reshaemye_metodom_ploschadej

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 1 

Зачетные работы по содержанию факультативного курса

 

Зачётная работа по теме «Вспомогательная окружность»

1.                  В выпуклом четырёхугольнике ABCD угол ABC равен 111^◦, угол CBD равен 49^◦, угол ACD равен 62^◦. Найдите углы CAD и ADC.

2.                  В остроугольном треугольнике ABC проведены высоты AA1 и BB1, пересекающиеся в точке H. Известно, что угол CAB равен 70^◦, а угол ABC равен 80^◦. Найдите углы треугольников CA₁B₁ и A₁BH.

3. 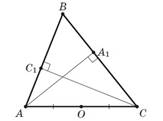                 В остроугольном треугольнике ABC проведены высоты AA1 и CC1; O—середина стороны AC, длина которой равна 10 см. Найдите расстояние от точки O до точек A1 и C1.

 

 

 

 

 

4.                  В треугольнике ABC проведены высоты AA1 и BB1. Найдите угол AA1B1, если угол ABB1 равен 40^◦.

 

5.                  Вне прямоугольника ABCD отмечена точка H так, что угол BHD равен 90^◦. Найдите угол AHC. 

Указание. Точки A, B, H, C, D лежат на одной окружности.

 

6.                  В выпуклом четырёхугольнике ABCD известно, что угол ABC равен 112^◦, угол ABD равен 48^◦, угол CAD равен 64^◦. Найдите угол ACD.

 

7.                  В выпуклом четырёхугольнике ABCD известно, что угол BAD равен 100^◦, угол BCD равен 80^◦, угол CAD равен 60^◦. Найдите угол CDB.

 

8.                  Внутри угла с вершиной O взята точка A. Точки B и C — проекции точки A на его стороны. Найдите углы треугольника ABC, если луч OA образует со сторонами данного угла углы 30^◦ и 40 ^◦ .

 

9.                  В треугольнике ABC проведены высоты AA1 и CC1. Найдите углы треугольника A1BC1, если углы BAC и BCA соответственно равны α и γ. 

Указание. Рассмотрите случаи, когда треугольник остроугольный и тупоугольный (B тупой).

 

10.              На сторонах треугольника ABC вне его построены равносторонние треугольники. Вокруг равносторонних треугольников описаны окружности с центрами в точках O1, O2 и

O3.  Докажите, что все три описанные окружности имеют общую точку (например, точку

F). 

Указание. Рассмотрите две окружности с центрами в точках O1 и O2; вычислите углы AFB и BFC. После этого легко доказать, что Окр(O3) проходит через точку F.

 

 

 

Зачётная работа. Методы решений задач по теме «Площади»

 

1.                  Найдите площадь параллелограмма, стороны которого равны 4 и 6, а угол между диагоналями равен 60^◦.  Указание. При решении полезно использовать метод геометрических преобразований.

 

2.                  В треугольнике ABC на стороне BC взята точка D, а на стороне AB — точка E. Прямая DF, параллельная AB, пересекает AC в точке F, а прямая DE, параллельная AC, пересекает AB в точке E. Докажите, что площади треугольников EDF и BDF равны.  Указание. При решении используйте метод сравнения площадей.

 

3.                  В параллелограмме ABCD с площадью S на стороне CD отмечена точка M так, что  CM : MD=1 : 2. Точка K—середина стороны AB, а точка P—середина стороны AD. Найдите площадь треугольника PKM.

 

4.                  В треугольнике ABC, площадь которого равна P, на стороне AB отмечена точка D, а на стороне BC—точка E так, что DE ‖ AC. Найдите площадь четырёхугольника BEMD, если точка M принадлежит AC, а площадь треугольника BDE равна Q.

 

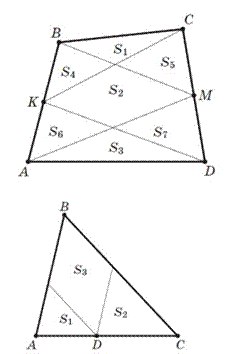
5.                  В выпуклом четырёхугольнике ABCD точка K — середина стороны AB, а точка M —середина стороны CD. Отрезки KC, KD, MA, MB делят четырёхугольник на части, площади которых равны S1, S2, S3, S4, S5, S6, S7 (рис.). Докажите, что S₂ =S₁ +S₃. 

Указание.       Используйте метод перекрывающихся площадей.

 

 

 

6.                  На стороне треугольника ABC выбрана точка D, и через неё проведены прямые, параллельные сторонам AB и BC. По площадям S1 и S2 образовавшихся треугольников найдите площадь S3 образовавшегося параллелограмма

(рис.). 

 

 

Указание. При решении используйте метод подобия.

 

 

 

7.                  На плоскости треугольника ABC найдите множество точек M, для которых площади треугольников MAB, MBC, MAC равны.

 

8.                  AK—биссектриса угла BAC треугольника ABC. Найдите площадь этого треугольника, если AK = 12, AB = 14, AC = 35.  Указание. При решении используйте метод равных площадей.

 

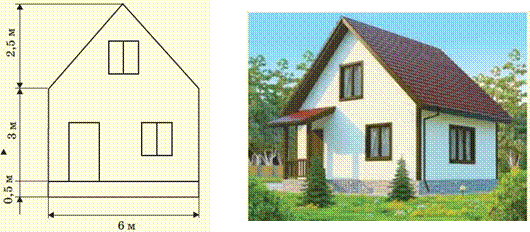
9.                  (задача практического содержания) Необходимо покрасить дом, изображенный на рисунке. Фундамент дома представляет собой квадрат со стороной 6 м. В доме имеется: 5 малых окон с размерами 1 м 50 см x 80 см, два больших окна с размерами 2 м 50 см x 80 см и дверь с размерами 2 м x 0,8 м.

По размерам, данным на чертеже (рис.), определите:

а) общую площадь той части стен дома, которые нужно покрасить;

б) сколько килограммов краски потребуется, чтобы покрасить стены дома в 2 слоя, если на покраску 1 м2 в один слой уходит 250 г краски;

в) какое оптимальное число пластиковых ведер краски необходимо купить, если в строительном магазине имеется нужная краска для фасадов по 5 л и 11 л.

 

Зачетная работа по теме «Метод подобия. Теорема Менелая. Теорема Чевы»

1.                  Решите задачу двумя способами—с использованием и без использования теоремы Менелая сравните способы. На сторонах AB и BC треугольника ABC взяты точки M и N так, что отношение длин отрезков AM и MB равно 2, отношение длин отрезков BN и NC равно 3. Пусть прямые MN и AC пересекаются в точке P. Найдите PC, если сторона AC равна 10.

2.                  В треугольнике ABC на сторонах AB и BC взяты точки K и M. Прямая KM пересекает прямую AC в точке P. Найдите отношение CP : PA , если AK : KB =2, BM : MC = 1 : 3.

Решите задачу двумя способами.

3.                  Докажите, что прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжений боковых сторон, делит основания трапеции пополам.

4.                  В треугольнике ABC на стороне AC отмечены точки P и E, на стороне BC—точки M и K так, что AP : PE : EC=CK : KM : MB. Докажите, что точка O пересечения отрезков AM и BP, точка T пересечения отрезков AK и BE и вершина C лежат на одной прямой.

5.                  Н а сторонах BC и AC треугольника ABC взяты точки A₁ и B₁ так, что BA₁ : A₁C = 1 : 3, CB₁ : B₁A = 1 : 2. Пусть K—точка пересечения отрезков AA₁ и BB₁. Найдите отношение AC₁ : C₁B, где C₁—точка пересечения CK и AB.

6.                  В треугольнике ABC на продолжении стороны AC за точку C взята точка N так, что CN = AC. Точка K—середина стороны AB. В каком отношении прямая KN делит сторону BC?

7.                  На сторонах AB и AC треугольника ABC взяты такие точки M и N, что AM : BM =        CN : NA = 1 : 2. Отрезки BN и CM пересекаются в точке K. Найдите отношения BK : KN и            CK: KM. 

Указание. Примените теорему Менелая сначала к треугольнику CAM и секущей BK, а затем к треугольнику ABN и секущей CK.

8.                  На медиане CM треугольника ABC взята точка P. Прямые AP и BP пересекают стороны BC и AC соответственно в точках A1 и B1. Докажите, что отрезок A1B1 параллелен AB и делится медианой CM пополам. 

 

 

Зачётная работа по теме «Комбинация методов»

(Задачи на вычисление)

 

 

 

 

 

 

 

 

 

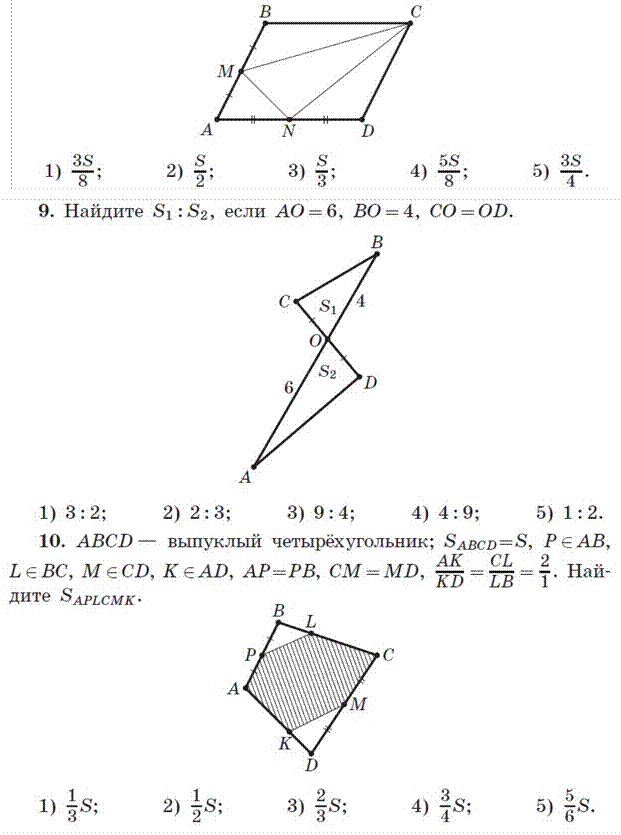
Приложение 2 

Промежуточное тестирование по теме «Опорные факты, связанные с равновеликостью и отношением площадей»

 

 

 

 

 

 

 

Приложение 3 

Методическая разработка занятия 

 

Тема: Метод перекрывающихся площадей

Тип урока: Урок изучения нового материала Формируемые результаты занятия:

 Предметные: формировать умение применять метод перекрывающихся площадей при решении задач.

Личностные: формировать умение планировать свои действия в соответствии с учебным заданием.

Метапредметные: формировать умение устанавливать причинно- следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы.

Планируемые результаты: Учащийся научится применять метод перекрывающихся площадей при решении задач.

Основные понятия: Площадь треугольника, площадь четырехугольника, свойства площадей, метод площадей, перекрывающиеся площади.

Описание хода урока

I.                   Организационный момент. (2 мин)

Приветствие. Проверка готовности класса к занятию. Использование педагогических приёмов наведения дисциплины в классе.

 

II.                Постановка цели и задач урока. Формулирование темы урока.

 

Форма организации учебной деятельности: фронтальная

 

Слайд 1

 

 

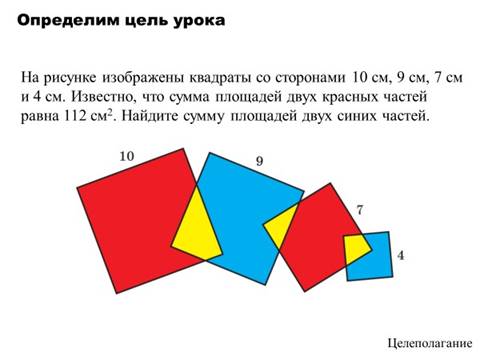
Вопросы для построения диалога:

Каково взаимное расположение квадратов на рисунке? [квадраты наложены друг на друга]

Что можете сказать про площади желтых частей? [площади желтых частей являются общей частью площади двух квадратов – синего и красного]

Как бы вы назвали площади желтых фигур? [перекрывающиеся]

Что требуется найти? [площадь синих квадратов]

Как можно назвать метод решения данной задачи, исходя из специфичного расположения фигур? [Метод перекрывающихся площадей] Сформулируйте тему занятия. [Метод перекрывающихся площадей]

Сформулируйте цель занятия. [Применение метода перекрывающихся площадей при решении задач]

Что мы должны сделать чтобы достичь данной цели? Сформулируйте задачи занятия.

[Задачи занятия:

1.      Сформулировать и усвоить суть метода перекрывающихся площадей.

2.      Научиться, используя свойства площадей, выражать площади перекрывающихся фигур.

3.      Научиться решать задачи с помощью метода перекрывающихся площадей.]

 

III.      Актуализация опорных знаний (Вхождение в тему урока и создание условий для осознанного восприятия нового материала)

Форма организации учебной деятельности: фронтальная

Приём: Решение задач на готовых чертежах

Слайд 2

 

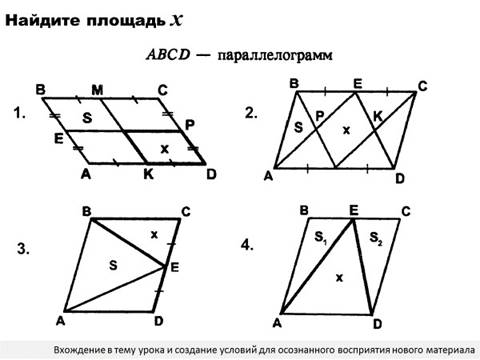
Вопросы (к слайду 2) для построения диалога:

1.      Какие свойства площадей вы использовали для нахождения площади x?

2.      Какое дополнительное построение необходимо сделать для параллелограмма, чтобы установить зависимость площади параллелограмма и треугольников? 3. Найдите равновеликие и равносоставленные фигуры в каждой комбинации 1-4.

   

 

Слайд 3

 

 

 

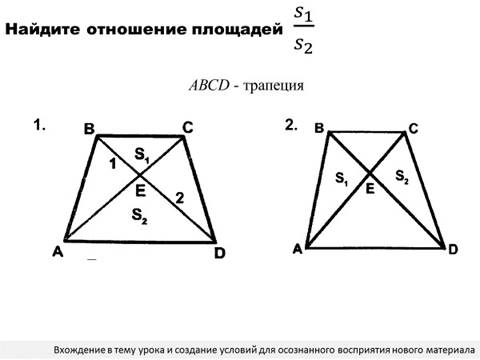
IV.             Мотивация учебной деятельности

Форма организации учебной деятельности: индивидуальная

Приём: «Мотивационные вопросы»

✓  Как я планирую организовать свою работу на занятии?

✓  При каких условиях занятие будет для меня полезным?

✓  Где я буду применять знания и умения, получаемые на данном занятии?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V.                Решение заданий (Организация и самоорганизация учащихся. Организация обратной связи) Форма организации учебной деятельности: фронтальная, парная

 

Ресурсный материал по содержанию урока	Этапы организации деятельности учащихся при решении задач	Результат деятельности учащихся (по этапам)	Помощь учителя
1. Дано: ABCD—параллелограмм; E∈BC, F∈AD; AE∩BF=M, ED∩FC=N. Доказать:  а) SAMF +SFND = SBME +SENC; б) SMENF =SABM +SNCD.	1)                 Постановка учебной цели в процессе решения задачи; 2)                 выявление средств, необходимых для решения задачи;   3)                 соотнесение выявленных средств выполнения              учебно- познавательной деятельности (далее -УПД) с собственными знаниями и умениями, принятие решения о помощи, выбор уровня самостоятельности; 4) поиск решения задачи;	1)                 Найти и обобщить способ решения данной задачи;   2)                 Перечисляют: а) свойства площадей;      б) формулы для вычисления площадей;       в) приём работы с задачей: выведение следствий из условия и требования. 3)                 Формулируют свойства площадей; записывают формулы для вычисления площади параллелограмма, треугольника.             4)                 Работа с текстом задачи: анализируют условие и чертеж; изображают фигуру в соответствии с условием задачи, записывают данные и требование: «Дано», «Доказать».  Поиск решения задачи: Выводят следствия из условия задачи:  Точки E∈BC, F∈AD, причем BC ‖ AD, то можно использовать свойство площадей треугольников в параллелограмме. Выводят следствия из требования: для доказательства а) нужно на чертеже найти фигуру, которая была бы составлена из данных	Помогает назвать нужные теоретические факты и этапы решения задачи.                   Предлагает: ✓  Постараться вспомнить, что ещё известно про площади фигур; ✓  Придумать, какие фигуры должны получиться при разбиении и пересекающихс

 

5)              составление решения задачи;                             6)              реализация плана;

плана

треугольников      –      такие      фигуры      есть      - 𝛥𝐵𝐹𝐶 и 𝛥𝐴𝐸𝐷. Если поиск решения задачи не закончен – то выбирают способ помощи и уровень помощи.  1           уровень:         воспользоваться       идеей           метода решения: перекрывающиеся площади. 2                уровень: воспользоваться перечнем обоснований, необходимых для решения задачи; 3                уровень: по готовой схеме поиска решения задачи           вспомнить      формулировки           теорем            – обоснований и разобрать решение задачи. 5) Составляют план решения: А)  1.              Доказать SBFC = SAED 2.              Используя свойство площадей, записать чему равны площади треугольников 𝛥𝐵𝐹𝐶 и 𝛥𝐴𝐸𝐷. 3.              Выделить       пересекающиеся       площади           в 𝛥𝐵𝐹𝐶 и 𝛥𝐴𝐸𝐷. 4.              Используя свойство аддитивности, доказать требуемое утверждение. Б) 1.              Дополнительное построение: провести высоту к основанию АD. 2.              Доказать, что  SABF +SFCD= 0,5 SABCD. 3.              Доказать, что SABF +SFCD = SBFC. 4.              Используя свойство аддитивности, площадей доказать требуемое утверждение. 6) Записывают решение задачи. Обобщают решение задачи. Фиксируют в устной речи созданный приём: 1. Найти равновеликие фигуры с пересекающимися площадями или сделать дополнительное построение, чтобы их найти; 2. Выяснить, из каких частей состоят искомые

я площадях.                                                       Даёт образец решения для контроля. Помогает правильно сформулировать отдельные шаги приёма.

 

	7)                 контроль             решения задачи;     8)                 Оценка процесса и результатов выполненной деятельности, с использованием соответствующих приёмов; 9)                 Коррекция собственной УПД	фигуры; 3.                  Найти (доказать равенство) площади фигур, входящих в искомую фигуру; 4.                  Используя свойство аддитивности площадей, выразить площадь искомой фигуры через известные площади фигур.   7)                 перечисляют все определения, свойства и теоремы, которые использовались при решении задачи.    8)                 Оценивают свою деятельность при решении задачи по пяти бальной системе.       9)                 Фиксирует свое внимание на ошибке и устанавливает её характер, анализирует причины ошибки – применение теоретических положений (определения, теоремы, формулы), делает вывод о причине ошибки, использует откорректированные знания и действия в процессе решения аналогичных задач.	Предлагает перечислить умения, которые использовались. Предлагает зафиксировать оценку на листке контроля.     Предлагает коррекцию собственных учебных действий выполнить дома.
2. Точки Е, F, К, L - середины сторон четырехугольника АВСD.  Докажите, что сумма площадей треугольников АLМ, ВNЕ, СРF, КQD равна площади четырехугольника МNРQ.		1)                 Применение приёма (метода) решения задачи 1 к решению данной задачи; 2)                 Перечисляют: а) свойства площадей;      б) формулы для вычисления площадей;       в) приём работы с задачей: выведение следствий из условия и требования. 3)                 Формулируют         свойства         площадей; записывают формулы для вычисления площади параллелограмма, треугольника. 4)                 Работа с текстом задачи: анализируют условие и чертеж; изображают фигуру в	Помогает назвать нужные теоретические факты и этапы решения задачи.       Предлагает: ✓ Постараться

 

соответствии с условием задачи, записывают данные и требование: «Дано», «Доказать». Осуществляют поиск решения задачи (выводит следствия из условия и следствия из требования; выясняет какие дополнительные построения можно выполнить, чтобы получить равновеликие фигуры с перекрывающимися площадями).           5)                 Составляют план решения. 6)                 Записывают решение задачи.     7)                 перечисляют все определения, свойства и теоремы, которые использовались при решении задачи.    8)                 Оценивают свою деятельность при решении задачи по пяти бальной системе.     9)                 Фиксирует свое внимание на ошибке и устанавливает её характер, анализирует причины ошибки – применение теоретических положений (определения, теоремы, формулы), делает вывод о причине ошибки, использует откорректированные знания и действия в процессе решения аналогичных задач.

вспомнить, что ещё известно про площади фигур; ✓ Придумать, какие фигуры должны получиться при разбиении и пересекающихс я площадях.   Даёт образец решения для контроля. Предлагает другой способ решения. Предлагает перечислить умения, которые использовались. Предлагает зафиксировать оценку на листке контроля.   Предлагает коррекцию собственных учебных действий выполнить дома.

VI.             Проверка полученных результатов. Коррекция

Форма организации учебной деятельности: индивидуальная

Решение самостоятельно заданий по вариантам (№ 1 – I вариант, № 2 – II вариант) и последующей проверкой решения по эталону.

1.       Дано: ABCD — квадрат; N∈AD, M∈CD; отрезки BN, CN, BM, AM делят квадрат на части с площадями S1 — S8.

             Сравнить: площади S₁ и S₃ +S₆ +S₇.

 

 

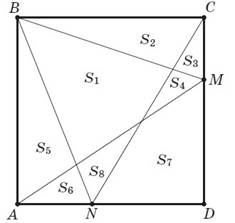
2.       Дано: ABCD—трапеция (BC ‖ AD); BB₁ ‖CC₁, B₁, C₁ ∈ AD; отрезки AC, BD, BB₁, CC₁ делят трапецию на части с площадями S1—S8. Доказать: S₄ =S₁ +S₂ +S₃.

 

 

  

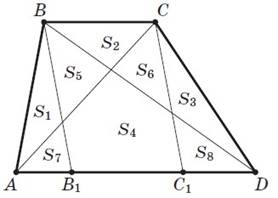
VII. Подведение итогов урока. Рефлексия

✓  Какой метод решения планиметрических задач вы использовали сегодня на занятии?

✓  Какие пробелы в своих знаниях я заметил на уроке?

✓  Можно ли сказать, что я научился применять метод перекрывающихся площадей при решении задач? 

✓  Над чем нужно поработать дома?

 

VIII.                      Домашнее задание: Решить задачу на использование метода перекрывающихся площадей. Дан выпуклый четырехугольник ABCD. Середины сторон АВ и CD обозначены соответственно через К и М, точку пересечения отрезков ВМ и СК – через Р, точку пересечения отрезков АМ и DК – через О. Докажите, SMOKP = S_▲BPC + S_▲AOD.

31