Программа внеурочной деятельности для учащихся 7 класса " Тайны Математики"

Государственное бюджетное общеобразовательное учреждение

 

средняя общеобразовательная школа № 311 с углубленным изучением физики

 

Фрунзенского района Санкт-Петербурга

 

 

РАССМОТРЕНА на заседании методического совета ГБОУ СОШ № 311 Протокол №___ от «___» августа 20___ Председатель МО: ________________(Ф.И.О.)		ПРИНЯТА на Педагогическом совете ГБОУ СОШ № 311 Протокол №____ от «___» августа 20___		УТВЕРЖДАЮ Директор ГБОУ СОШ № 311 _______В.Л. Виноградова Приказ №____ от «___» августа 20___
СОГЛАСОВАНО Зам.директора по УВР ________________(Ф.И.О.) «___» августа 20___

 

 

Рабочая программа

курса внеурочной деятельности

«Математическая мозаика»

(Общеинтеллектуальное направление)

 

 

 

 

Класс: 6

 

Срок реализации: 2018/2019 учебный год

 

 

Разработчик:

 

Михайлова Е.А

Учитель математики

 

 

 

 

 

 

 

 

 

 

Санкт-Петербург

 

2018

 

 

Пояснительная записка

 

Программа курса направлена на формирование универсальных (метапредметных) умений, навыков, способов деятельности, которыми должны овладеть обучающиеся, на развитие познавательных и творческих способностей и интересов, которые определены Федеральным государственным образовательным стандартом основного общего образования.

Рабочая программа детализирует и раскрывает содержание тем, а также учитывает возрастные особенности обучающихся, уровень развития их познавательных способностей, специфику образовательного учреждения.

 

ПРАВОВАЯ ОСНОВА РАЗРАБОТКИ И УТВЕРЖДЕНИЯ РАБОЧЕЙ ПРОГРАММЫ

1. Закон Российской Федерации от 29.12.2012 г. № 273 – ФЗ «Об образовании в Российской Федерации»;

2. Приказ Министерства образования и науки Российской Федерации от 17.12.2010 № 1897 «Об утверждении федерального государственного образовательного стандарта основного общего образования» с последующими изменениями;

3. Методические рекомендации Министерства образования и науки Российской Федерации от 18.08.2017 № 09-1672 «По организации содержания внеурочной деятельности в рамках реализации основных общеобразовательных программ, в том числе в части проектной деятельности»;

4.  Инструктивно-методическое письмо от 21.05.2015 «Об организации внеурочной деятельности при реализации федеральных государственных образовательных стандартов начального общего и основного общего образования в образовательных организациях Санкт-Петербурга»;

5. Постановление Федеральной службы по надзору в сфере защиты прав потребителей и благополучия человека и Главного государственного санитарного врача Российской Федерации от 29.12.2010 № 189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях»;

6. Образовательная программа ГБОУ СОШ № 311 с углубленным изучением физики Фрунзенского района Санкт-Петербурга;

7. Положение о рабочей программе курса внеурочной деятельности ГБОУ СОШ № 311 с углубленным изучением физики Фрунзенского района Санкт-Петербурга;

8. Учебный план ГБОУ СОШ № 311 с углубленным изучением физики Фрунзенского района Санкт-Петербурга на 2018-2019 учебный год.

 

Цель и задачи курса

Формирование у обучающихся интереса к математике как науке и на основе соответствующих заданий развитие их математических способностей и внутренней мотивации к предмету.

      Задачи программы:

·         развивать логическое и творческое мышление, интеллект обучающихся;

·         расширять кругозор обучающихся;

·         повышать степень вовлеченности обучающихся в учебно-творческую деятельность;

·         пробуждать активность исследовательских и познавательных интересов;

·         cформировать навыки исследовательской работы при решении нестандартных задач и задач повышенной сложности;

·         повышать математическую культуру учащихся.

 

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ  освоения  курса и Формы их учёта

 

По окончании изучения курса «Математическая мозаика» рабочая программа обеспечивает достижение обучающимися следующих личностных, метапредметных и предметных результатов:

  Личностными результатами реализации программы станет формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества, а также формирование и развитие универсальных учебных умений самостоятельно определять, высказывать, исследовать и анализировать, соблюдая самые простые общие для всех людей правила поведения при общении и сотрудничестве (этические нормы общения и сотрудничества).

Метапредметными результатами реализации программы станет формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности, а именно следующих универсальных учебных действий.

Регулятивные УУД:

· Самостоятельно формулировать цели занятия после предварительного обсуждения.

· Учиться совместно с учителем обнаруживать и формулировать учебную проблему.

· Составлять план решения проблемы (задачи).

· Работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки.

· В диалоге с учителем учиться вырабатывать критерии оценки и определять степень успешности выполнения своей работы и работы всех, исходя из имеющихся критериев.

Познавательные УУД:

· Ориентироваться в своей системе знаний: самостоятельно предполагать, какая информация нужна для решения той или иной задачи.

· Отбирать необходимые для решения задачи источники информации среди предложенных учителем словарей, энциклопедий, справочников, интернет-ресурсов.

· Добывать новые знания: извлекать информацию, представленную в разных формах (текст, таблица, схема, иллюстрация и др.).

· Перерабатывать полученную информацию: сравнивать и группировать факты и явления; определять причины явлений, событий.

· Перерабатывать полученную информацию: делать выводы на основе обобщения знаний.

· Преобразовывать информацию из одной формы в другую: составлять более простой план учебно-научного текста.

· Преобразовывать информацию из одной формы в другую: представлять информацию в виде текста, таблицы, схемы.

Коммуникативные УУД:

· Донести свою позицию до других: оформлять свои мысли в устной и письменной речи с учётом своих учебных и жизненных речевых ситуаций.

· Донести свою позицию до других: высказывать свою точку зрения и пытаться её обосновать, приводя аргументы.

· Слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения.

· Читать вслух и про себя тексты научно-популярной литературы и при этом: вести «диалог с автором» (прогнозировать будущее чтение; ставить вопросы к тексту и искать ответы; проверять себя); отделять новое от известного; выделять главное; составлять план.

· Договариваться с людьми: выполняя различные роли в группе, сотрудничать в совместном решении проблемы (задачи).

· Учиться уважительно относиться к позиции другого, учиться договариваться.

 

Предметными результатами реализации программы станет создание фундамента для математического развития, формирование механизмов мышления, характерных для математической деятельности, а именно:

· познакомиться со способами решения нестандартных задач по математике;

· познакомиться с нестандартными методами решения различных математических задач;

· освоить логические приемы, применяемые при решении задач;

· рассуждать при решении логических задач, задач на смекалку, задач на эрудицию и интуицию

· познакомиться с историей развития математической науки, биографией известных ученых-математиков.

· расширить свой кругозор, осознать взаимосвязь математики с другими учебными дисциплинами и областями жизни;

·  познакомиться с новыми разделами математики, их элементами, некоторыми правилами, а при желании самостоятельно расширить свои знания в этих областях;

· познакомиться с алгоритмом исследовательской деятельности и применять его для решения задач математики и других областей деятельности;

· приобрести опыт самостоятельной деятельности по решению учебных задач;

· приобрести опыт презентации собственного продукта.

 

Формы учёта результатов

ЛИСТ индивидуальных достижений учащегося_______ 6__класса по курсу внеурочной деятельности «Математическая мозаика»

 

	Сентябрь	Октябрь	Ноябрь	Декабрь	Январь	Февраль	Март	Апрель	Май
Посещаемость
Выполнение заданий на занятии
Сообщения и мини доклады
Выполнение практических работ
Самооценка учащегося

В конце каждой четверти и в году выставляется зачет или не зачет по итогом листа индивидуальной деятельности

 

СОДЕРЖАНИЕ КУРСА

 

Четность и нечетность. (4 часа)

Понятие четности. Применение идеи четности: известные утверждения. Четность суммы и разности нескольких чисел. Идея «разбиения на пары».

Задачи, в которых используется понятие четности встречаются очень часто. Поэтому желательно познакомить школьников с подходами к решению этих задач. Задачи естественным образом разбиваются на три цикла:

1.      Разбиение на пары.

Если предметы разбиты на пары, то их четное число. Следовательно, если из нечетного числа предметов образовано несколько пар, то, по крайней мере, один предмет остался без пары. Для решения таких задач нужно в каждом случае увидеть, что именно и на какие пары разбивается.

2.      Чередование.

Если из предметов двух сортов образована цепочка, в которой соседние предметы разных сортов, то на всех четных местах стоят предметы одного сорта, а на всех нечетных – другого. Отсюда вывод: предметов одного сорта на один больше, чем предметов другого сорта в случае, когда длина цепочки нечетна и предметов обоих сортов поровну, тогда длина цепочки четна.

3.      Чет – нечет.

Решение задач основано на простом наблюдении: сумма четного числа нечетных чисел – четна. Обобщение этого факта: четность суммы нескольких чисел зависит лишь от четности числа нечетных слагаемых: если количество нечетных слагаемых (не)четно, то и сумма – (не)четна.

Примеры задач:

ü За круглым столом сидят мальчики и девочки. Докажите, что количество пар соседей разного пола чётно.

ü На плоскости расположено 11 шестерёнок, соединенных в кольцо. Могут ли все шестерёнки вращаться одновременно?

ü Шахматный конь вышел с поля a1 и через несколько ходов вернулся на него. Докажите, что он сделал чётное число ходов.

ü Может ли прямая не содержащая вершин замкнутой 11-звенной ломаной, пересекать все ее звенья?

ü На клетчатой бумаге нарисован замкнутый путь, идущий по линиям сетки. Может ли он иметь длину 1999? А длину 2000?

ü Улитка ползет по плоскости с постоянной скоростью, поворачивая на 90 каждые 15 минут. Докажите, что она может вернуться в исходную точку только через целое число часов.

ü Из набора домино выбросили все кости с «пустышками». Можно ли оставшиеся кости выложить в ряд по правилам?

ü Пусть расположение шашек в предыдущей задаче симметрично относительно обеих диагоналей. Докажите, что одна из шашек стоит в центральной клетке.

 

Логические задачи.(8  часов)

Среди задач на сообразительность особый интерес представляют логические задачи. Если для решения задачи требуется лишь логически мыслить и совсем не нужно производить арифметические выкладки, то такую задачу обычно называют логической. При решении подобных задач решающую роль играет правильное построение цепочки точных, иногда очень точных рассуждений.

На первом этапе целесообразно  рассмотреть три  широко распространенных типа логических задач:

1.      Задачи, в которых на основании серии посылок, сообщающих те или иные сведения о действующих лицах, требуется сделать определенные выводы.

2.      Задачи о «мудрецах».

3.      Задачи о лжецах и тех, кто всегда говорит правду.

 

Софизмы ( 6 часов)

Софизмы – это умышленные ложные умозаключения, которые имеют вид правильных. Они обязательно содержат одну или несколько замаскированных логических ошибок. Например, в математических софизмах часто выполняются «запрещенные» действия, такие как деление на ноль, не учитываются условия применимости формул и правил. 

Софистика – направление философии, которое возникло в V-IV вв. до н.э. в Греции и стало очень популярным а Афинах. Софистами называли платных «учителей мудрости», которые учили граждан риторике, искусству слова, приемам ведения спора, красноречию. Одним из представителей софистов был философ Протагор, который говорил: «Я обучаю людей риторике, а это и есть гражданское искусство».

Софисты считали, что истина субъективна, то есть у каждого человека своя истина, человек сам создает себе истину и сам же её оценивает, поэтому в суждениях об истине очень много личного. Справедливость, как и истина, у каждого человека тоже своя, а значит, о каждой вещи можно судить двояко, то есть о каждой вещи есть два противоположных мнения. Софисты учили людей оценивать одно и то же событие, как положительное и как отрицательное одновременно, таким образом они приучали людей к широте взглядов. Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки «вне речи», то есть в мышлении.

Учащимся предлагаются для решения не только широко известные софизмы, но ставится задача сконструировать (придумать) свои софизмы.

 

Арифметика остатков ( 4 часа)

Тема является чрезвычайно важной, хотя и может показаться несколько скучной. Для первого этапа работы вполне достаточно тех теоретических сведений, которые имеют учащиеся 6 класса. В процессе работы теоретическая база может быть несколько пополнена, однако увлекаться теорией не следует. При решении задач выделяются те свойства целых чисел, которые помогают добраться до ответа. Методика работы:

Первый этап: учащиеся должны понять, что свойства делимости полностью определяются разложением числа на простые множители. Этому могут помочь следующие ключевые вопросы:

ü   делится ли 3⁵ *2 на 3;

ü   делится ли 3⁵ *2 на 4;

ü   делится ли 3⁵ *2 на 5;

ü   делится ли 3⁵ *2 на 6?

ü   верно ли, что если натуральное число делится на 4 и на 6, то оно делится на 24?

ü   число 5А делится на 3. Верно ли, что А делится на 3?

ü   число А – четно. Верно ли, что 3А делится на 6?

ü   число А  не делится на 3. Может ли на 3 делится число 2А? и т.п.

Далее актуализируются определения взаимно простых чисел, наибольшего общего делителя и наименьшего общего кратного, определение деления одного целого числа на натуральное число с остатком.

 

 

Игры ( 14  часов)

На занятиях внеурочной деятельности рассматриваются так называемые «конечные игры с полной информацией», теория которых проста и доступна школьникам. На занимательном материале учащиеся знакомятся с такими важными понятиями теории игр, как «стратегия» и «выигрышная стратегия», а также на простом и наглядном примере «изоморфизма игр» - с важнейшим для все математики понятием изоморфизм.

Поиск выигрышной стратегии требует настойчивости и упорства в достижении поставленной цели, развивает логические, комбинаторные и вычислительные способности учащихся.

Первый класс игр – игры-шутки. Это игры, исход которых не зависит от того, как играют соперники. Игры-шутки позволяют снять напряжение и усталость, дают школьникам возможность переключиться от напряженной творческой работы. Целесообразно предлагать их по одной после разбора трудного материала. Полезно перед решением, дать школьникам возможность  поиграть друг с другом.

Задачи – игры весьма содержательны. При изложение их решения, необходимо, во-первых, грамотно сформулировать стратегию, а  во-вторых, доказать, что она, действительно, ведет к выигрышу. Поэтому, задачи-игры чрезвычайно полезны для развития  речевой математической культуры и четкого понимания того, что значит решить задачу.

 

Принцип Дирихле( 4 часов)

При решении многих задач используются сходные между собой приемы рассуждений. Очевидно, что если в каждую клетку разрешается посадить не более одного зайца, то разместить 6 зайцев в 5-ти клетках не удастся и вообще, ни для какого натурального  n не удастся разместить n+1 зайцев в n клетках. Можно сказать иначе: если в n клетках находится n+1 зайцев, то найдется клетка, в которой сидит не менее двух зайцев.

Сформулированное выше утверждение о зайцах-клетках имеет следующий математический смысл: при отображении множества А, содержащего n+1 элементов  в множество В, содержащее n элементов, найдутся два элемента  множества А, имеющие один и тот же образ. Это утверждение называется принципом Дирихле. Принцип Дирихле, несмотря на всю простоту и очевидность очень часто используется при доказательстве теорем и решении задач.

При разборе задач полезно четко разделять доказательство на поиск «зайцев» и «клеток», на дополнительные соображения и, наконец, на применение принципа Дирихле.

 

Графы ( 8 часов)

Теория графов находит свое применение в различных областях современной математики и ее многочисленных приложений, особенно экономике. Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность. Многие доказательства также упрощаются, приобретают убедительность, если воспользоваться графами, особенно это относится к комбинаторике.

Понятие графа должно появиться на занятии после того, как разобрано несколько задач, решающее соображение в которых – графическое изображение условия.

Первая и главная цель, которую нужно преследовать, занимаясь графами, - научить школьников видеть граф в условии задачи и грамотно переводить это условие на язык теории графов. Кроме того, важно, чтобы учащиеся правильно применяли  теорему о четности числа нечетных вершин графа, понимали, что такое компонента связности и умели пользоваться критерием Эйлеровости.

 

Геометрия:  задачи на разрезание (6 часов)

Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих задач на разрезание были найдены еще с древними греками и китайцами. Первый систематический трактат на эту тему принадлежит перу Абул-Вефа – персидского астролога X века. Геометры всерьез занялись решением задач на разрезание фигур на наименьшее число частей и последующее составление из них той или иной новой фигуры лишь в XX веке, прежде всего, потому, что универсального метода решения таких задач не существует и каждый, кто берется за их решение, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению. Учитывая, что здесь не требуется глубокое знание геометрии, любители могут иногда даже превзойти профессионалов-математиков.

Задачи на разрезание помогают как можно раньше формировать геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе.

На первом этапе рекомендуется рассмотреть задачи на клетчатой бумаге. Задачи, в которых разрезание фигур (в основном это квадраты и прямоугольники) идет по сторонам клеток.

Далее могут рассматриваться задачи, связанные с фигурами-пентамино. Пентамино́, изначально, (от др.-греч. πέντα пять, и домино) — пятиклеточные полимино, то есть плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами («ходом ладьи»). Сегодня пентамино понимается более широко – плоская фигура, составленная из плиток.

Задачи разбиения плоскости, в которых нужно находить сплошные разбиения прямоугольников на плитки прямоугольной формы, задачи на составление паркетов, задачи о наиболее плотной укладке фигур в прямоугольнике или квадрате, задачи, в которых одна фигура разрезается на части, из которых составляется другая фигура.

В наши дни любители головоломок увлекаются решением задач на разрезание, п

Примеры задач:

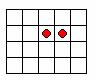
ü Разрежьте фигуру, изображенную на рисунке, на две равные части по линиям сетки так, чтобы в каждой из частей был кружок.

ü На клетчатой бумаге нарисован квадрат размером 5*5 клеток. Придумайте, как разрезать его по линиям сетки на 7 различных прямоугольников.

 

Комбинаторика( 10 часов)

В последние годы необычайно возросла роль комбинаторных методов не только в самой математике, но и в ее многочисленных приложениях: физике, химии, биологии, лингвистике, технике, экономике. Поэтому важно как можно раньше начать знакомить учащихся  с комбинаторными методами и комбинаторными подходами. Изучение этой темы способствует развитию у учащихся «комбинаторного» мышления.

Главная цель, которую должен преследовать  педагог при разборе и решении этих задач – осознанное понимание школьниками в какой ситуации при подсчете вариантов следует перемножать, а в какой – складывать. Для этого следует демонстрировать учащимся комбинаторные методы на большом  количестве простых и конкретных примеров, продвигаясь вперед осторожно и постепенно. Не следует переходить к введению понятий «размещение» и «перестановки» пока это правило не освоено всеми учащимися.

 

 

Повторение. Математическое соревнование. Метаматематическая карусель (4 часа)

По окончании цикла занятий проводится обобщающее занятие, в рамках которого проходит повторение изученного материала, а также проводится один из видов математического соревнования, который наиболее подходит для организации работы со школьниками, занятыми во внеурочной деятельности. Это может быть математический КВН, математический аукцион, математическая регата, игра по станциям, математический хоккей, математическое лото, мозговая атака и другие формы работы.

 

 

 

 

КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

 

Сроки	№	Тема занятия	Форма проведения занятия	Количество часов
				теория	практика
05.09	1	Математическое домино	Обсуждение  Практикум	1	1
12.09	2	Логика и не только	Обсуждение  Практикум	1	1
19.09	3	Принцип Дирихле	Практикум соревнование	1	1
26.09	4	Делимость и остатки	Обсуждение  Практикум	1	1
03.10	5	Признаки делимости	Практикум соревнование	1	1
10.10	6	Краски и раскраски	Обсуждение  Практикум	1	1
17.10	7	Графы и графини	Обсуждение  Практикум	1	1
24.10	8	Математическая регата	Практикум соревнование	1	1
07.11	9	Задачи о разном	Обсуждение  Практикум	1	1
14.11	10	Задачи о пути и движении	Обсуждение  Практикум	1	1
21.11	11	Время. Календарь. Возраст	Обсуждение  Практикум	1	1
28.11	12	«Много» и «мало»	Игра	1	1
05.12	13	Комбинаторные задачи	Беседа лабораторный практикум	1	1
12.12	14	И снова графы	Исследовательская работа	1	1
17.12	15	Сравнения и комбинаторика	Обсуждение  Практикум	1	1
24.12	16	Математическая карусель	Игра	1	1
16.01	17	Посчитаем, поиграем	Практикум соревнование	1	1
23.01	18	Выигрышные и проигрышные стратегии	Исследовательская работа	1	1
30.01	19	Симметрия	Обсуждение конструирование	1	1
06.02	20	Шахматы и доски	Игра	1	1
13.02	21	Четность	Обсуждение  Практикум	1	1
20.02	22	Чередование	Практикум соревнование	1	1
27.02	23	Задачи-шутки	Игра	1	1
06.03	24	Задачи о турнирах	Обсуждение  Практикум	1	1
13.03	25	Математический футбол	Игра	1	1
20.03	26	Логические задачи	Обсуждение конструирование	1	1
03.04	27	Перебор в логических задачах	Обсуждение  Практикум	1	1
10.04	28	Кто есть кто?	Практикум соревнование	1	1
17.04	29	Остров рыцарей и лжецов	Практикум соревнование	1	1
24.04	30	Африканские игры	Игра	1	1
01.05	31	Как придумывают задачи	Обсуждение  Практикум	1	1
08.05	32	Логика и не только	Обсуждение  Практикум	1	1
15.05	33	Математическая карусель	Практикум соревнование	1	1
22.05	34	Математическая карусель	Практикум соревнование	1	1

 

 

Методическое и информационное обеспечение

Основная

 

1.      Анфимова Т.Б. Математика. Внеурочные занятия. 5-6 классы. – М.: Илекса, 2011.

2.      Вакульчик П.А. Сборник нестандартных задач. – Минск: БГУ, 2001.

3.      Генкин С.А., Итенберг И.В., Фомин Д.В. Математический кружок. Первый год. – Л.: С-Петербургский дворец творчества юных, 1992.

4.      Екимова М.А., Кукин Г.П. задачи на разрезание. – М.: МЦНМО, 2005.

5.      Игнатьев Е.И. В царстве смекалки. – М.: Наука, 1979.

6.      Канель-Белов А.Я., Ковальджи А.К. Как решают нестандартные задачи. – М.: МЦНМО, 2015.

7.      Математический кружок. Первый год обучения, 5-6 классы (Коллектив авторов). – М.: Изд. АПН СССР, 1991.

8.      Руденко В.Н., Бахурин Г.А., Захарова Г.А. Занятия математического кружка в 5 классе. – М.: Изд. дом «Искатель», 1999.

9.      Спивак А.В. Математический кружок. 6-7 классы. – М.: Посев, 2003.

10.  Спивак А.В. Математический праздник. – М.: МЦНМО, 1995.

11.  Столяр  А. А. Зачем и что мы доказываем в математике. – Минск: Народная асвета, 1987.

12.  Шарыгин И.Ф., Шевкин А.В. Математика. Задачи на смекалку. 5-6 кл. – М.: Просвещение, 2001.

13.  Шейкина О.С., Соловьева Г.М. Математика. Занятия школьного кружка. 5-6 кл. – М.: НЦ ЭНАС, 2003.

 

Дополнительная

1. Спивак А.В. Математический кружок. – М.: МЦНМО, 2015.
2. Гарднер М. А ну-ка догадайся! – М.: Мир, 1984.
3. Гарднер М. Есть идея! – М.: Мир, 1982.
4. Гарднер М. Крестики-нолики. – М.: Мир, 1988.
5. Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1971.
6. Гарднер М. Математические досуги. – М.: Мир, 1972.
7. Гарднер М. Математические новеллы. – М.: Мир, 1974.
8. Гарднер М. Путешествие по времени. – М.: Мир, 1990.
9. Гик Е.Я. Замечательные математические игры. – М.: Знание, 1987.
10. Гусев В.А., Орлов А.И., Розенталь А.Л. Внеклассная работа по математике в 6-8 классах.  -  М.: Просвещение, 1984.
11. Кноп К. А. Взвешивания и алгоритмы: от головоломок к задачам. - М., МЦНМО, 2011.  
12. Кордемский Б.А. Математическая смекалка. – М., ГИФМЛ, 1958.
13. Линдгрен Г. Занимательные задачи на разрезание. – М.: Мир, 1977.
14. Пойа Д. Как решать задачу. – М.: Учпедгиз, 1961.
15. Пойа Д. Математика и правдоподобные рассуждения. – М.: Наука, 1975.
16. Пойа Д. Математическое открытие. – М.: Наука, 1970.
17. Радемахер Г.Р., Теплиц О. Числа и фигуры.  – М.: Физматгиз, 1962.
18. Смаллиан Р. Алиса в стране  Смекалки – М.: Мир, 1987.
19. Смаллиан Р. Как же называется эта книга? – М.: Мир, 1981.
20. Смаллиан Р. Принцесса или тигр? – М.: Мир, 1985.
21. Смыкалова Е.В. Необычный урок математики. – СПб.: СМИО Пресс, 2007.
22. Уфнаровский В.Л. Математический аквариум. – Кишинев: Штиинца, 1987.
23. Фарков А.В. Математические олимпиады: методика подготовки 5-8 классы. – М.: ВАКО, 2012.
24. Агаханов Н. X. Математика. Районные олимпиады. 6—11 классы / Агаханов Н.X., Подлипский О.К. — М.: Просвещение, 2010.

 

 

 

Лист коррекции рабочей программы

Курс внеурочной деятельности: Математическая мозаика

Класс: 6

Учитель: Михайлова Е.А

2018/2019 учебный год

По плану			После коррекции
№ занятия	Тема	Часы	№ занятия	Тема	Часы
Утверждена приказом № 32/2 от «28»апреля 2019 года
33-34	Математическая карусель	4	33	Математическая карусель	2

 

Учитель:     (подпись)          Михайлова Е.А