Программа

(внеурочной деятельности,

дополнительного образования)

в рамках летней интеллектуально оздоровительной школы 2019

«Школа магии и чародейства»

по олимпиадной математике для учащихся 5-8 класса

Предметная область: математика

 

 

 

 

 

 

 

 

Составитель: Руднева Н.Н.

 Учитель математики

МБОУ г. Иркутска Лицей № 1

 

 

г. Иркутск , 2019

Оглавление

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.. 3

ПЛАНИРУЕМЫЕ ОБРАЗОВАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ... 4

СОДЕРЖАНИЕ ПРОГРАММЫ... 4

ТЕМАТИЧЕСКИЙ ПЛАН.. 5

СПИСОК ЛИТЕРАТУРЫ... 6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

 

Среди многочисленных приемов работы, ориентированных на интеллектуальное развитие обучающихся, особое место занимает подготовка к предметным олимпиадам.

Данная программа позволяет учащимся в рамках летнего интеллектуально-оздоровительного лагеря (далее - ЛИОШ) ознакомиться с интересными вопросами математики, выходящими за рамки школьной программы, расширить целостное представление о проблеме данной науки. Решение математических задач, связанных с логическим мышлением, закрепит интерес детей к познавательной деятельности, будет способствовать развитию мыслительных операций и общему интеллектуальному развитию.

Основная функция занятий по олимпиадной математике – формирование представлений об идеях и методах решения отдельных классов задач; развитие творческих способностей у школьников, осознанных мотивов учения.

Содержание программы соответствует познавательным возможностям школьников и предоставляет им возможность работать на уровне повышенных требований, развивая учебную мотивацию.

Программа направлена на расширение и углубление знаний по предмету. В результате занятий учащиеся должны приобрести навыки и умения решать более трудные и разнообразные задачи олимпиадного уровня.

Цель курса:

·         ознакомление учащихся с некоторыми методами и приемами решения олимпиадных задач;

·         развитие творческого потенциала школьников, их способностей к плодотворной умственной деятельности;

·         расширение и углубление знаний учащихся по математике.

Задачи курса:

Общеобразовательные: формировать навыки решения задач олимпиадной математики с использованием различных методов:

·         Четность;

·         Делимость и остатки;

·         Принцип Дирихле;

·         Инвариант и раскраски.

Развивающие:

·         Развитие познавательного интереса;

·         Развитие логического мышления, наблюдательности, воображения, математической интуиции;

·         Развитие умственных способностей: гибкости, критичности, самостоятельности и широты мышления, памяти, способности к генерированию идей, укрупнению информации.

Воспитательные:

·         Развитие и углубление познавательного интереса к олимпиадной математике, стимулирование самостоятельности учащихся при решении задач по олимпиадной математике.

Основными формами организации учебно-познавательной деятельности являются практикумы.

Программа курса составлена на одну смену ЛИОШ для двух групп обучающихся (1 группа-   5-6 классы, 2 группа – 7-8 классы) в объеме по 6 часов для каждой группы.

 

ПЛАНИРУЕМЫЕ ОБРАЗОВАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ

 

Курс направлен на развитие у обучающих логического мышления, позволяющего переформулировать математическую задачу основываясь на теории чисел, свойствах суммы, разности чисел, находить способ решения нестандартных задач по теории чисел и решении задач олимпиадного типа.

Личностных результатов: ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, распознавать логически некорректные высказывания.

Метапредметных результатов:

·         Умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

·         Умение адекватно описывать правильность и ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;

·         Умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы.

Предметных результатов:

·         Овладение приемами решения задач по основным разделам содержания.

·         Умение применять знания из теории чисел для решения задач олимпиадной математики.

 

СОДЕРЖАНИЕ ПРОГРАММЫ

 

1 ГРУППА (5-6 КЛАСС)

1.       Чётность (1 ЧАСА)

Цель: создать условия для развития навыков поиска одинаковой идеи решения, основанной на чётности, чётности суммы и разности, произведения, в задачах с различными условиями, сути построения доказательства утверждений.

Чётность. Чётность суммы или разности чисел. Чётность произведения чисел.

2.      Делимость (1 ЧАСА)

Цель: создать условия для развития навыков поиска идеи решения, основанной на делимости, свойствах делимости суммы, разности и произведения, в задачах с различными условиями.

Делимость. Отсечение невозможных вариантов

3.      Принцип Дирихле (2 ЧАСА)

Цель: создать условия для применения принципа Дирихле при решении задач в разных условиях.

Принцип Дирихле. Переформулировка принципа Дирихле для площадей и покрытия фигур.

4.      Инвариант и раскраски (2 ЧАСА)

Цель: создать условия для развития навыка анализировать состояние системы, определять, что является в данной системе инвариантом.

Инвариант. Вспомогательные раскраски.

 

 

2 ГРУППА (7-8 КЛАСС)

 

1.      ИНВАРИАНТ (2 ЧАСА)

Цель: создать условия для развития навыка анализировать состояние системы, определять, что является в данной системе инвариантом, выполнять задания для построения инварианта.

 

Инвариант. Построение инвариантов.

2.      ПОЛУИНВАРИАНТ (1 ЧАС)

Цель: создать условия для развития навыка анализировать изменения состояние системы, определять, что является в данной системе полуинвариантом, осуществлять выбор полуинварианта.

 

Полуинвариант. Выбор полуинварианта.

3.      ТУРНИРЫ (2 ЧАСа)

Цель: создание условия для развития навыка решения заданий по турнирам в различных схемах турнира, с заданной системой подсчета очков.

 

Схема турнира. Схема подсчета очков. Примеры и контрпримеры. Принцип Дирихле в заданиях на турниры.

4.      ОЛИМПИАДНАЯ ГЕОМЕТРИЯ (1 ЧАСА)

Цель: создание условия для развития навыка решения олимпиадных заданий по геометрии на нахождения площадей фигур.

 

 Площади фигур.

ТЕМАТИЧЕСКИЙ ПЛАН

занятий по олимпиадной математике в рамках ЛИОШ (сезон 2019)

№ занятия	Тема занятия	Количество часов
1 ГРУППА (5-6 КЛАСС)
1	Чётность. Чётность суммы или разности чисел. Чётность произведения чисел	1
2	Делимость. Отсечение невозможных вариантов	1
3	Принцип Дирихле	1
4	Переформулировка принципа Дирихле для площадей и покрытия фигур	1
5	Инвариант	1
6	Вспомогательные раскраски	1
	Итого:	6 часов
2 ГРУППА (7-8 КЛАСС)
1	Инвариант	1
2	Построение инварианта	1
3	Полуинвариант. Выбор полуинварианта	1
4	Схема турнира. Схема подсчета очков. Примеры и контрпримеры. Принцип Дирихле в заданиях на турниры.	1
5	Турниры	1
6	Площади	1
	Итого:	6 часов

СПИСОК ЛИТЕРАТУРЫ

 

Математический кружок 6 класс. / Универсальная методическая разработка для элективного курса по решению нестандартных задач в средних образовательных учреждениях г. Москвы // Сост. Д.А. Коробицын, Г.К. Жуков. – М.: МГУ, 2017

Математический кружок 5-6 классы. / Универсальная методическая разработка для элективных курсов по решению нестандартных задач в средних образовательных организациях // Сост. И.И. Осипов. – М.: МГУ, 2017

Математический кружок, 6-7 классы, 1-е полугодие (15 занятий) / Методическое пособие для выявления и развития математических способностей обучающихся // Сост.                             Н.П. Стрелкова, С.Л. Кузнецов. – М.: МГУ, 2017

Математический кружок 8 классы. / Универсальная методическая разработка для элективных курсов по решению нестандартных задач в средних образовательных организациях // Сост. А.Л. Канунников. – М.: МГУ, 2018

Математический кружок (7 класс, I полугодие). Часть II: Методические указания / Универсальная методическая разработка для элективного курса по решению нестандартных задач в средних образовательных учреждениях г. Москвы // Сост. Е.А. Асташов, Я.А. Верёвкин, А.А. Дейч, С.М. Саулин, А.В. Феклина. – М.: МГУ, 2017

 

СПИСОК ИНТЕРНЕТ РЕСУРСОВ

 

Делимость http://www.ashap.info/Uroki/KirovLMSH/1999/14-Delimost.pdf

Олимпиадная математика. Инвариант. 8 класс. http://www.vk.com/mathin1580

Принцип Дирихле http://www.ashap.info/Uroki/KirovLMSH/1999/11-Dirichle.pdf

Процессы. Полуинвариант www.ashap.info/Uroki/KirovLMSH/2012/index.html

Чётность http://www.ashap.info/Uroki/KirovLMSH/1999/09-Chetno.pdf

 

 

 

 

 

 

 

 

 

Приложение 1

 

ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ К ЗАНЯТИЯМ

5-6 класс

Чётность

«Знакомство в Школе чародейства и волшебства»

 

Идея занятия: Четность, важное свойство, которое легко отслеживать, и которое позволяет отсекать невозможные случаи, используя свойства четности суммы, разности и произведения, разбиения на пары, чередования.

Основные свойства четности:

1.      Произведение любого (целого) числа на чётно число чётно.

2.      Произведение двух нечётных чисел нечётно.

3.      Сумма двух чисел разной чётности нечётна.

4.      Сумма двух чисел одной чётности чётна.

 Раздаточный материал № 1-2.

Свойство разбиения на пары:

Если предметы можно разбить на пары, то их количество чётно.

 Раздаточный материал № 4-8.

Свойства чередования:

1.      Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их чётное число (и каждого вида поровну).

2.       Если в некоторой замкнутой цепочке чередуются объекты двух видов:

·         начало и конец цепочки разных видов, то в ней чётное число объектов,

·         начало и конец одного вида, то нечётное число.

3.      Обратно: По чётности длины чередующейся цепочки можно узнать, одного или разных видов её начало и конец.

Раздаточный материал № 9-11.

 

РАЗДАТОЧНЫЙ МАТЕРИАЛ

Презентация  в МS РР

1.                  «Письма и волшебные превращения». 13 листов писем - приглашений, присланных «Мистеру Г. Поттеру, графство Суррей, город Литтл Уингинг, улица Тисовая, дом 4, чулан под лестницей», дядя Вернон разорвал или на 3, или на 5 частей. Затем некоторые из листов опять разорвал  или на 3, или на 5 частей, и так несколько раз.  С его слов после всего этого получилось 100 листов?  Мог ли он получить 100 листов, если не являлся волшебником?

2.                  При отправке в Хогвартс студенты должны иметь с собой десять монет магической валюты достоинством в 1, 3 и 5 кнатов. В магической лавке Рон Уизли подал на размен 1 сикль, с просьбой получить десять монет вышеуказанного достоинства. Однако, Рону отказали в выполнении такого условия. Правомерно ли поступил сотрудник магической лавки? Справочно: Обменный курс магических валют следующий: 1 сикль = 29 кнатов.

3.                Волшебная Распределяющая шляпа приветствует вас, участники Школы чародейства и волшебства ЛИОШ 2019, и просит вас пройти испытание и ответить на вопрос. Верно ли, что если каждый из вас совершит с другими участниками нечетное число рукопожатий, то вас –   четное число?

4.                  На шахматной доске стоят 11 фигур волшебных шахмат, расположенных симметрично относительно большой диагонали. Есть фигура или фигуры и на большой диагонали?

5.                  Может ли шахматный конь пройти с поля a1 на поле h8, побывав по дороге на каждом из остальных полей ровно один раз? Справочно: волшебная шахматная доска совпадает с обычной.

6.                  Студенческий парламент состоит из представителей факультетов Гриффиндор и Слизерин, причём они представлены одинаковой численностью студентов. На совместном заседании парламента присутствовали все, и никто не воздержался при голосовании. Когда было объявлено, что некоторое решение было принято большинством в 23 голоса, представители Гриффиндора закричали: «Это обман!». Почему?

7.                  В конференции магов принимало участие 19 волшебников. После конференции каждый из них отправил четыре или два письма другим ученым, бывшим на конференции. Каждый из участников по прибытии домой получил по три письма. Хорошо ли сработала почтовая служба?  Все ли письма дошли до адресатов?

8.                  В магической лавке задумались над оригинальной выкладкой волшебных палочек, которые до этого хранились в мешке. Всего было четыре волшебные палочки длины 11 см, две палочки длины 12 см, семь палочек длины 13 см и  пять палочек длины 14 см. Продавец хочет сложить из них  прямоугольник, использовав все палочки. Удастся ли ему это?  (Ломать волшебные палочки нельзя).

9. 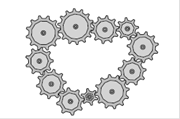                 Гарри отдал в ремонт остановившиеся карманные часы – символ факультета Гриффиндор.  Часовщик был изумлен, увидев, что в механизме одиннадцать шестерёнок соединены в замкнутую цепочку так, как показано на рисунке. Что вызвало удивление у часовщика?

10.              Магический браслет волшебника начального уровня состоит из 237 звеньев, к каждому из которых прикреплен магический шарм одного из двух видов. Получит ли Гермиона браслет, в котором два шарма одного вида будут рядом?

11.              В клетчатом квадрате, на котором была изображена карта Хогвартса и его окрестностей, разрезая по границам клеток, прорезали квадратную дырку поменьше - территория без магии.  Может ли оставшаяся фигура состоять ровно из 250 клеток, для применения в каждом по одному виду магических заклинаний?

Делимость. Отсечение невозможных вариантов

«Магическое заклинание»

Идея занятия: показать, что делимость является легко проверяемым свойством, которое можно использовать для отсечения невозможных вариантов. На основе заданий по теме расшифровать магическое заклинание, позволяющее сделать невидимые чернила видимыми и узнать, кто его применял и для чего (Апарекиум, Гермиона Грейнджер, заклинание применялось для того, чтобы узнать, что скрывает дневник Тома Реддла).

Основные понятия: простое число, составное число, делитель, делимое, признаки делимости.

Свойства делимости произведения, суммы и разности:

1.    Если один из множителей делится на некоторое число, тои всё произведение делится на это число.

2.      Если каждое слагаемое делится на некоторое число, то и сумма делится на это число.

3.      Если уменьшаемое и вычитаемое делятся на некоторое число, то и разность делится на это число.

4.      Если одно из двух слагаемых делится на некоторое число, а другое – нет, то сумма на это число не делится.

Раздаточный материал

Решение задач на скорость за определенное время, тот кто верно решил задачу получает право открыть одну букву в слове, если в результате оказались не все буквы, то вместе решаем не решенные задачи и открываем оставшиеся буквы (9 задач, 9 букв).  Далее определяем смысл заклинания, кто, и при каких обстоятельством использовал его.

1.      Чтобы открыть сейф в банке «Гринготтс», нужно ввести код — число, состоящее из семи цифр: двоек и троек. Сейф откроется, если двоек больше, чем троек, а код делится и на 3, и на 4 Придумайте код, открывающий сейф.

2.      Можно ли волшебными монетами в 14 и 35 галлеонов заплатить без сдачи сумму в 2019 галлеонов?

3.      Волшебный банк «Гринготтс» - хранит сбережения волшебников. По запросу одного из вкладчиков были выданы шесть мешков с золотыми галлеонами, проверяя содержимое мешков выяснилось, что в первых четырёх мешках оказалось по 60, 30, 20 и 15 золотых монет. Когда подсчитали монеты в оставшихся двух, кто-то заметил, что число монет в мешках составляет некую последовательность. Приняв это к сведению, волшебник точно сказал, сколько монет в пятом и шестом мешках? Как он это сделал?

4.      Гермиона для приготовления магического зелья приобрела в лавке несколько лягушек по 35 пенсов, несколько бутылочек бесовского зелья по 1 фунту 40 пенсов за штуку и змею за 2 фунта 80 пенсов. Продавец сказал, что с неё 20 фунтов 50 пенсов. Гермиона обиделась и превратила продавца в мышку. Докажите, что было за что.

5.      В справочнике «Магия для чайников» написано: Замените в слове ЗЕМЛЕТРЯСЕНИЕ одинаковые буквы на одинаковые цифры, а разные — на разные. Если полученное число окажется простым, случится настоящее землетрясение. Возможно ли таким образом устроить землетрясение? (Натуральное число, большее 1, называется простым, если у него нет других делителей, кроме 1 и самого себя.)

6.      При подготовке праздничного магического шествия Хагрид решил построил эльфов Хогвартса в колонну по 4, но при этом женщина-эльф Винки осталась лишней. Тогда Хагрид построил эльфов в колонну по 5. И снова Винки осталась лишней. Когда же и в колонне по 6  Винки опять осталась лишней, Хагрид посулил ей работу на кухне вне очереди, после чего в колонне по 7 Винки нашла себе место и никого лишнего не осталось. Какое наименьшее количество эльфов могло быть в Хогвартсе?

7.      Жители Хогвартса, как и мы с вами, делят сутки на несколько часов, час на несколько минут, а минуту на несколько секунд. Маховик времени опять сбился, и у них в сутках стало 77 минут, а в часе 91 секунда. Сколько стало секунд в сутках в Хогвартсе?

8.      Маленькие детки кушали конфетки. Каждый съел на 7 конфет меньше, чем все остальные вместе, но всё же больше одной конфеты. Сколько всего конфет было съедено?

9.      Студенты 1 курса, построенные парами, возвращаются с вечернего чая с пряниками в карманах. В каждой паре у одного пряников вдвое больше, чем у другого. Может ли у всех вместе быть ровно 1000 пряников?

 

 

Принцип Дирихле

«Торжественно клянусь, что замышляю шалость и только шалость!»

Идея занятия: показать применение принципа Дирихле: если кроликов в клетках больше, чем клеток, то найдется клетка с не менее чем двумя кроликами, при решении задач. Искусство применения состоит в умении понять, что считать клетками, а что - кроликами. Приобщить учащихся к оценкам, рассуждениям от противного и неконструктивных доказательств. 

Принцип Дирихле:

Если в n «клетках» сидят не менее n+1 «кроликов», то в какой-то из «клеток» сидят не менее 2-х «кроликов».

Различные усиления, обобщения принципа Дирихле:

1. Если в n клетках сидят не более n-1 кроликов, то есть пустая клетка.
Доказывается методом от противного.

2. Если в n клетках сидят ровно n кроликов, то либо в каждой клетке сидит ровно один кролик, либо есть и пустая клетка, и клетка, в которой не менее 2-х кроликов.
(!) П.2 очень полезен в тех случаях, когда мы знаем, что ровно по одному кролику в каждой клетке сидеть не может.

3. Если в n клетках сидят не менее n ∙ (k – 1) + 1 кроликов, то в какой-то из клеток сидят не менее k кроликов.

4. Если в n клетках сидят не более n ∙ (k+1) – 1 кроликов, то в какой-то из клеток сидят не более k кроликов.

Правила оформления решения:

На принцип Дирихле при решении задач на олимпиаде можно прямо ссылаться, на обобщения и усиления - не рекомендуется. Легче подставить в нужное место решения доказательство соответствующего утверждения. Слова «принцип Дирихле» в таком случае можно вообще не упоминать.

Раздаточный материал

Восстановите цитату:

 

,

!

 

Данное заклинание раскрывало истинную природу объекта (карта мародёров) и перед вами появится полная карта Хогвартса и его окрестностей. Созданная Сириусом Блэком, Джеймсом Поттером, Римусом Люпином и Питером Петтигрю - бандой бывших учеников Хогвартса, карта проявляет не только всю территорию замка школы магии, но и секретные проходы и потайные комнаты.

Единственным недостатком артефакта является то, что он показывает не все части замка. Поскольку ученики, создавшие карту, не смогли нанести на нее места, где сами никогда не бывали. Так, например, в ней отсутствует тайная комната и выручай-комната, однако это мощный инструмент для тех, кто хочет скрытно пробраться в любую часть замка.

 

    1.   На факультет Гриффиндор – 400 учеников. Докажите, что хотя бы двое из них родились в один день года.

    2.   В школе магии Хогвартс 30 классов и 1000 первокурсников. Докажите, что есть класс, в котором не менее 34 первокурсников.

    3.   В классе 30 учеников. Во время контрольной работы по зельеварению Рон сделал 13 ошибок, а остальные – меньше. Докажите, что найдутся три ученика, сделавшие одинаковое число ошибок.

    4.   Тыквенное печенье — одно из самых популярных лакомств в волшебном мире. Его можно купить в «Сладком королевстве» или же сделать самостоятельно. Для праздника нужно 9 ящиков тыквы одного сорта, в ближайший магазин привезли 25 ящиков с тыквами трех сортов, причем в каждом ящике лежали тыквы одного сорта. Найдутся ли 9 ящиков одного сорта?

    5.   В ящике лежат носки: 10 чёрных, 10 синих, 10 белых. Какое наименьшее количество носков надо вынуть не глядя, чтобы среди вынутых оказалось два носка а) одного цвета; б) разных цветов; в) чёрного цвета?

    6.   Хагрид хоть и не очень умел готовить, но всё делал от души. Его «каменные кексы» (Rock Cakes), кстати, — классический британский десерт, названный так не из-за жёсткости, а из-за внешнего вида, ведь напоминают они обломки скал. В его рецепт входили: сливочное масло, овсяные хлопья, мука, сахар, сухофрукты и измельчённые орехи.  Собрав ингредиенты для приготовления печенья было обнаружено, что орехи отсутствуют, пятнадцати мальчикам поручили собрать вместе сто орехов. Докажите, что какие-то двое из них должны собрать одинаковое количество орехов.

    7.   В поисках философского камня, способного превращать любые металлы в золото и являющегося средством для приготовления эликсира жизни, на карьере собрали 36 камней. Их веса соответственно 490 кг, 495 кг, 500 кг, …, 665 кг (арифметическая прогрессия). Можно ли увезти эти камни на семи трёхтонных грузовиках?

    8.   Волшебник решил сыграть в лотерею «6 из 49», какое наименьшее число карточек спортлото «6 из 49» ему надо купить, чтобы наверняка хоть на одной из них был угадан хоть один номер?

 

Переформулировка принципа Дирихле для площадей и покрытия фигур

«Мантия - невидимки»

Идея занятия: сформулировать утверждения принципа Дирихле и его расширений для площадей и покрытия фигур.

Основные утверждения:

Если фигура площади S покрыта несколькими фигурами с суммой площадей (строго!) больше S, то у нее имеется точка, покрытая не менее 2-х раз

1.                  Если фигура площади S покрыта несколькими фигурами с суммой площадей (строго!) меньше S, то у нее имеется точка, ни покрытая ни разу.
2. Если фигура площади S покрыта несколькими фигурами с суммой площадей ровно S, то либо каждая точка покрыта ровно один раз, либо есть и точка, не покрытая ни разу, и точка, покрытая не менее 2-х раз.

3. Если фигура площади S покрыта несколькими фигурами с суммой площадей (строго!) больше (k – 1) ∙ S, то у нее имеется точка, покрытая не менее k раз.

4. Если фигура площади S покрыта несколькими фигурами с суммой площадей (строго!) меньше (k + 1) ∙ S, то у нее имеется точка, покрытая не более k раз.

 

Правила оформления решения:

На принцип Дирихле при решении задач на олимпиаде можно прямо ссылаться, на обобщения и усиления - не рекомендуется. Легче подставить в нужное место решения доказательство соответствующего утверждения. Слова «принцип Дирихле» в таком случае можно вообще не упоминать.

Раздаточный материал

На вопрос «Какой из Даров Смерти вы бы предпочли?» Гермиона Грейнджер ответила, что её. Что она имела в виду? («Мантию-невидимку») Ключ: этот предмет сделан из лёгкой, серебристой ткани. Не рвётся от заклинаний и не поддаётся Манящим чарам. Ключ выдается при условии решения всех пяти задач.

 

1. В ковре размером 4´4 метра моль проела 15 дырок. Докажите, что из этого ковра можно вырезать коврик размера 1´1 метр, в котором нет ни одной дырки.

2. В прямоугольнике 5 х 6 закрашена 19 клеток. Докажите, что в нём можно выбрать квадрат 2х 2, в котором закрашено не менее трёх клеток.

3. На площади 1 км х 1 км растёт сосновый лес, состоящий из 4500 деревьев диаметром 50 см каждое. Докажите, что на этом квадратном участке можно разместить 50 прямоугольных площадок 10 м х 20 м, на которых не растёт ни одного дерева.

4. В ковре размером 3х3 м. Коля проделал 8 дырок. Докажите, что из него можно вырезать коврик размером 1х1, не содержащий внутри себя дырок (дырки можно считать точечными).

5. Альбус Дамблдор пообещал студентам Гринффиндора открыть великую тайну, если он составит чудесный квадрат 6 х 6 из чисел +1, -1, 0 так, чтобы все суммы по строкам, по столбцам и по большим диагоналям были различны. Помогите юным волшебникам.

 

Дополнительные задания:

1.                  В классе 35 учеников. Можно ли утверждать, что среди них найдутся хотя бы 2 ученика, фамилии которых начинаются с одной буквы?

2.                  В лесу растет миллион елок. Известно, что на каждой из них не более 600 000 иголок. Докажите, что в лесу найдутся две елки с одинаковым количеством иголок.

 

Инвариант

«Магические игры»

Определение инварианта.

Инвариант – это что-то (число, свойство, величина), не изменяющееся при разрешенных действиях (сложение, вычитание, при разрезании не меняется сумма площадей частей фигуры).

Типичные инварианты: четность, остаток по какому-то модулю, произведение или сумма всех чисел или остатков и т.п.

Инварианты дружат с подсчетом двумя способами. Если разрешенные преобразования инвариант сохраняют, то нельзя получить ситуацию с другим значением инварианта (например, нельзя доехать на поезде от Стокгольма до Нью-Йорка, поскольку поезд не меняет континент).

Виды инвариантов:

Инварианты с четностью в решениях задач могут являться четностью суммы, разности, остатка, произведения, частного и др. Эти инварианты являются четностью некоторого объекта изначально или путем простейших преобразований, таких как умножение, деление, вычитание и сложение. Четность или нечетность результата этих операций очень часто влияет на решение задачи.

Инварианты с разбиением на пары чаще всего встречаются в геометрических задачах с пересекающей стороны фигуры ломанной.

Инварианты с раскраской объектов в 2 цвета можно встретить в тех задачах, где есть предпосылки для раскраски (например, круг, поделенный на несколько секторов) или где используется шахматное поле.

Инварианты с чередованием состояний объекта часто соседствуют с инвариантами на четность. Эти инварианты характеризуют несколько состояний объекта, которые всегда сменяют друг друга в определенном порядке. Например, мяч сначала летит к стене в одном направлении, а потом отскакивает от нее и летит в руки в другом направлении.

Алгоритм решения задач (после рассмотрения первой задачи сформулировать пошаговый алгоритм):

1.                  Удостоверьтесь, что ваша задача – инвариантная, ведь если это не так, то мой алгоритм окажется для вас бесполезным. В инвариантных задачах всегда бывают эксперименты: переворачивать что либо, считать довольно большие суммы чисел и другие похожие задания.

2.                  После того, как вы удостоверились, что ваша задача инвариантная, выполните условия эксперимента. Желательно несколько раз. Это очень важно! Только эксперимент поможет вам найти инвариант. Так что не поленитесь и на практике раскрасьте клетки, переверните стаканы или раздайте пирожки детям (кстати, это можно сделать и схематично, в тетради).

3.                  После выполнения условий детально разложите требуемые условия для решения задачи. Например, если все стаканы должны стоять правильно, то правильных стаканов будет n, а неправильных 0.

4.                  Затем попытайтесь найти что-либо неизменяемое во всех ваших экспериментах. Это должно быть логичным по отношению к вашим условиям для решения.

5.                  Соотнесите инвариант и условия для решения. Сделайте вывод исходя из этого соотношения. Например, число неправильных стаканов всегда нечетно, а их должно быть 0 – четное количество. Значит, все стаканы не могут стоять правильно.

6.                  Если вашего вывода достаточно для решения задачи, то вы правильно решили задачу с помощью нахождения инварианта. Если нет, то попробуйте дальше дополнить ее логичными рассуждениями и поисками. Бывает, что после нахождения инварианта нужно еще немного додумать задачу и все получится. В противном случае попробуйте найти инвариант еще раз.

Раздаточный материал

Презентация  в МS РР

1.                  Голодный удав разлёгся вокруг камня и с голодухи прикусил свой хвост. В это время кролик, пользуясь беспомощностью удава, начал издеваться над ним, перепрыгивая через лежащего удава на камень и обратно. Но через полчаса ему это надоело, и он пошёл домой, где с гордостью заявил, что ровно 357 раз перепрыгнул через бедное животное. Докажите, что он заблуждается.

2.                  Рон, Гарри и Гермиона придумали игру со следующими условиями: на доске написаны шесть чисел 1, 2, 3, 4, 5, 6. За один ход разрешается к любым двум из них одновременно добавить по единице. Игра заканчивается, когда в результате нескольких ходов все числа сделаются равными.  Выигрывает тот, кто последним ходом делает все числа равными.

3.                  На столе в банке стоят шесть столбиков монет. В первом столбике одна монета, во втором - две, в третьем - три, ..., в шестом - шесть.  Разрешается на любые два столбика положить по монете. Можно ли за несколько таких операций сделать все столбики одинаковыми?

4.                  В кабинете Северуса Снегга в ряд выставлены 100 баночек с зельем. Однообразность угнетала, он решился на эксперимент, каждый день менять местами две баночки, стоящие через одну.       У Снегга было желание с помощью таких операций переставить все баночки в обратном порядке. Эксперимент удался?

5.                  В комнате смешивания зелий колбы с зельями пронумерованы числами 1, 2, ..., 714 по порядку. Решив расставить колбы в обратном порядке (в связи с переносом стеллажей на противоположную сторону комнаты), решили менять местами колбы с числами, стоящими «через одно» (например, можно поменять 3 и 5). Можно ли с помощью таких перестановок расположить все колбы с зельем в обратном порядке?

6.                  Три клабберта на прямой играют в чехарду: каждую секунду один из них прыгает через какого - то другого (но не через двух).   Игра будет закончена, когда они все окажутся на том месте, с которого начинали игру. Могут ли они через 111 секунд закончить игру?

7.                  Рон, Гермиона и Гарри играли в слова. Каждый записывал по сто слов. После этого записи сравнивали. Если слово встречалось у всех троих, за него давали 0 очков, если у двоих -каждый получал 1 очко, если у одного - он получал 4 очка.  За подсчёт очков отвечал Рон. В результате его подсчётов сам Рон набрал 161, Гермиона – 180, а Гарри – 286 очков. Могло ли такое быть?

8.                  На столе стоят 7 стаканов вверх дном. За ход разрешается одновременно перевернуть любые 2 стакана. Можно ли за несколько ходов все стаканы поставить правильно?

9.                  На столе стоят 11 стаканов вверх дном. За ход разрешается одновременно перевернуть любые 6 стаканов. Можно ли за несколько ходов все стаканы поставить правильно?

Вспомогательные раскраски

«Практическая магия - Раскраска»

Инвариант и раскраски клетчатых досок.

Очень важный и стоящий несколько особняком класс задач на инвариант - какие-то преобразования на клетчатых досках. Либо мы ходит чем-нибудь по доске, либо заставляем доску фигурами. В любом случае, очень полезной может быть раскраска доски в два или более цветов, обладающая какими-то особыми свойствами. Рассматриваем три способа раскраски:

- шахматная (два цвета чередуются так, что любые две соседние по стороне клетки - разных цветов);

- «зебра» (чередование строк, выкрашенных в два цвета - или столбцов);

-  укрупненная шахматная (в шахматном порядке красятся не отдельные клетки, а целые блоки 2 х 2, 3 х 3 и т.д.).

На основании раскрашенной доски делаем вывод об инварианте.

Обход заданной фигуры:

Очень популярны задачи на шахматной доске, в которых используются как свойства шахматной раскраски, так и особенности «ходов» шахматных фигур. К свойствам шахматной доски относят общее количество клеток, количество черных и белых клеток в отдельности.

Идеи чередования при обходе заданной фигуры:

1. Если объекты двух видов чередуются, то количество объектов одного вида отличается от количества другого вида не более чем на 1.

2.  Если процесс (путь) начинается и заканчивается на одном и том же объекте, или начало и конец – объекты разного вида, то количество объектов каждого вида одинаковое, а число шагов – четное.

Задачи на обход заданной фигуры – задания №№ 1-3, 8, 9.

Задачи на замощение/разрезание – задание № 4.

Задания на построение раскраски по заданным условиям или на раскрашивание фигур, задачи об изменении положения объектов – задания №№ 5 – 7.

                                                  Раздаточный материал

К каждой задаче создается её геометрический образ, в виде заданной геометрической фигуры. Идеи раскрасок и решения задач предлагаются после проведения эксперимента и поиска инварианта для задачи.

1.      В прямоугольном доме (рис.1) 40 комнат и между каждыми двумя соседними комнатами – дверь. Можно ли пройти из в так, чтобы через каждую комнату проходить ровно один раз?

Рис. 1

Идеи решения: 1) раскрасим таблицу в шахматном порядке, тогда общее количество клеток можно рассматривать как совокупность белых и черных, 2) при каждом шаге цвет комнаты меняется на противоположный.

 

2.       Можно ли шахматным конем обойти доску 5 х 5, побывав в каждой клетке ровно по одному разу, и вернуться в начальную клетку?

Идеи решения: 1) раскрасить доску в шахматном порядке; 2) конь при каждом ходе

меняет цвет клетки на противоположный

 

3.       Шахматный король обошёл всю доску 6 х 6, побывав на каждой клетке ровно по одному разу и вернулся на исходную. Докажите, что он сделал чётное число диагональных шагов.

Идеи решения: 1) раскрасить доску в шахматном порядке; 2) после диагонального хода король не меняет цвет клетки, после прямого – меняет на противоположный.

 

4.      Можно ли выложить квадрат 8 х 8, используя 32 прямоугольника 2 х 1, чтобы 17 из них располагались горизонтально, а 15 – вертикально.

Идеи решения: 1) раскрасить квадрат, вертикально чередуя черный и белый цвет (раскраска «зебра»); 2) каждый прямоугольник 2 х 1 закрывает либо одну черную и одну

белую клетки, либо две клетки одного цвета.

 

5.       На доске 10 х 10 для «морского боя» стоит четырехпалубный корабль. Какое наименьшее число выстрелов необходимо сделать, чтобы наверняка ранить его?

Идеи решения: 1) раскрасить квадрат в 4 цвета; 2) любой прямоугольник 1 х 4 накрывает ровно по одной клетке каждого цвета.

 

6.       На каждой клетке доски 5 х 5 сидели бабочки. Вдруг, испугавшись громкого звука, они перелетели на соседние по стороне клетки. Обязательно ли осталась одна клетка свободная?

Идеи решения: 1) раскрасить доску в шахматном порядке; 2) каждая бабочка перелетает на клетку противоположного цвета.

 

7.       В клетках квадрата 3 х 3 расставлены числа. Разрешается к любым двум соседним (по стороне клетки) одновременно прибавлять или отнимать одно и то же число. Можно ли в какой-то момент получить второй квадрат?

 

Идеи решения: 1) раскрасить клетки каждого квадрата в шахматном порядке;

2)вычислить суммы чисел на клетках одного цвета; 3) прибавляя одно и то же число к

двум соседним клеткам, мы одновременно изменяем обе суммы.

 

8.      Можно ли обойти все города на рис., побывав в каждом городе ровно один раз? Точки на схеме — города, отрезки, их соединяющие — дороги между городами.

 

 

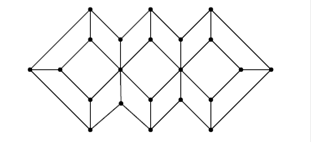
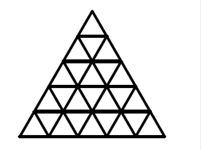
9.      Замок имеет форму правильного треугольника, разделенного на 25 маленьких залов той же формы. В каждой стене между залами проделана дверь. Путник ходит по замку, не посещая более одного раза ни один из залов. Найдите наибольшее число залов, которое ему удастся посетить.

 

 

 

 

 

 

 

 

 

 

 

7-8 класс

 

Инвариант

 

Определение инварианта.

Инвариант – это что-то (число, свойство, величина), не изменяющееся при разрешенных действиях (сложение, вычитание, при разрезании не меняется сумма площадей частей фигуры).

Типичные инварианты: четность, остаток по какому-то модулю, произведение или сумма всех чисел или остатков и т.п.

Инварианты дружат с подсчетом двумя способами. Если разрешенные преобразования инвариант сохраняют, то нельзя получить ситуацию с другим значением инварианта (например, нельзя доехать на поезде от Стокгольма до Нью-Йорка, поскольку поезд не меняет континент).

Виды инвариантов:

Инварианты с четностью в решениях задач могут являться четностью суммы, разности, остатка, произведения, частного и др. Эти инварианты являются четностью некоторого объекта изначально или путем простейших преобразований, таких как умножение, деление, вычитание и сложение. Четность или нечетность результата этих операций очень часто влияет на решение задачи.

Инварианты с разбиением на пары чаще всего встречаются в геометрических задачах с пересекающей стороны фигуры ломанной.

Инварианты с раскраской объектов в 2 цвета можно встретить в тех задачах, где есть предпосылки для раскраски (например, круг, поделенный на несколько секторов) или где используется шахматное поле.

Инварианты с чередованием состояний объекта часто соседствуют с инвариантами на четность. Эти инварианты характеризуют несколько состояний объекта, которые всегда сменяют друг друга в определенном порядке. Например, мяч сначала летит к стене в одном направлении, а потом отскакивает от нее и летит в руки в другом направлении.

Алгоритм решения задач (после рассмотрения первой задачи сформулировать пошаговый алгоритм):

1.      Удостоверьтесь, что ваша задача – инвариантная, ведь если это не так, то мой алгоритм окажется для вас бесполезным. В инвариантных задачах всегда бывают эксперименты: переворачивать что либо, считать довольно большие суммы чисел и другие похожие задания.

2.      После того, как вы удостоверились, что ваша задача инвариантная, выполните условия эксперимента. Желательно несколько раз. Это очень важно! Только эксперимент поможет вам найти инвариант. Так что не поленитесь и на практике раскрасьте клетки, переверните стаканы или раздайте пирожки детям (кстати, это можно сделать и схематично, в тетради).

3.      После выполнения условий детально разложите требуемые условия для решения задачи. Например, если все стаканы должны стоять правильно, то правильных стаканов будет n, а неправильных 0.

4.      Затем попытайтесь найти что-либо неизменяемое во всех ваших экспериментах. Это должно быть логичным по отношению к вашим условиям для решения.

5.      Соотнесите инвариант и условия для решения. Сделайте вывод исходя из этого соотношения. Например, число неправильных стаканов всегда нечетно, а их должно быть 0 – четное количество. Значит, все стаканы не могут стоять правильно.

6.      Если вашего вывода достаточно для решения задачи, то вы правильно решили задачу с помощью нахождения инварианта. Если нет, то попробуйте дальше дополнить ее логичными рассуждениями и поисками. Бывает, что после нахождения инварианта нужно еще немного додумать задачу и все получится. В противном случае попробуйте найти инвариант еще раз.

Раздаточный материал. Презентация

1.                  Голодный удав разлёгся вокруг камня и с голодухи прикусил свой хвост. В это время кролик, пользуясь беспомощностью удава, начал издеваться над ним, перепрыгивая через лежащего удава на камень и обратно. Но через полчаса ему это надоело, и он пошёл домой, где с гордостью заявил, что ровно 357 раз перепрыгнул через бедное животное. Докажите, что он заблуждается.

2.                  Рон, Гарри и Гермиона придумали игру со следующими условиями: на доске написаны шесть чисел 1, 2, 3, 4, 5, 6. За один ход разрешается к любым двум из них одновременно добавить по единице. Игра заканчивается, когда в результате нескольких ходов все числа сделаются равными.  Выигрывает тот, кто последним ходом делает все числа равными.

3.                  На столе в банке стоят шесть столбиков монет. В первом столбике одна монета, во втором - две, в третьем - три, ..., в шестом - шесть.  Разрешается на любые два столбика положить по монете. Можно ли за несколько таких операций сделать все столбики одинаковыми?

4.                  В кабинете Северуса Снегга в ряд выставлены 100 баночек с зельем. Однообразность угнетала, он решился на эксперимент, каждый день менять местами две баночки, стоящие через одну.       У Снегга было желание с помощью таких операций переставить все баночки в обратном порядке. Эксперимент удался?

5.                  В комнате смешивания зелий колбы с зельями пронумерованы числами 1, 2, ..., 714 по порядку. Решив расставить колбы в обратном порядке (в связи с переносом стеллажей на противоположную сторону комнаты), решили менять местами колбы с числами, стоящими «через одно» (например, можно поменять 3 и 5). Можно ли с помощью таких перестановок расположить все колбы с зельем в обратном порядке?

6.                  Три клабберта на прямой играют в чехарду: каждую секунду один из них прыгает через какого - то другого (но не через двух).   Игра будет закончена, когда они все окажутся на том месте, с которого начинали игру. Могут ли они через 111 секунд закончить игру?

7.                  Рон, Гермиона и Гарри играли в слова. Каждый записывал по сто слов. После этого записи сравнивали. Если слово встречалось у всех троих, за него давали 0 очков, если у двоих -каждый получал 1 очко, если у одного - он получал 4 очка.  За подсчёт очков отвечал Рон. В результате его подсчётов сам Рон набрал 161, Гермиона – 180, а Гарри – 286 очков. Могло ли такое быть?

8.                  На столе стоят 7 стаканов вверх дном. За ход разрешается одновременно перевернуть любые 2 стакана. Можно ли за несколько ходов все стаканы поставить правильно?

9.                  На столе стоят 11 стаканов вверх дном. За ход разрешается одновременно перевернуть любые 6 стаканов. Можно ли за несколько ходов все стаканы поставить правильно?

Построение инварианта

 

Типичная ситуация: есть набор позиций (состояний) и переходы между ними. Это можно рассматривать как граф. Пусть с каждой позицией можно связать некоторую величину. Если величина при переходах не меняется, она – инвариант. Значения инварианта разбивают граф на компоненты связности, и нет маршрута между позиций с разными значениями инварианта. Соответственно. можно доказывать невозможность действия: например, нельзя доехать на поезде от Нью-Йорка до Москвы, поскольку поезда из Америки ходят только в Америку. Но можно доказать и существование: если добраться-таки удалось, то был либо перелет, либо плавание.

Типичные инварианты: четность, общий делитель, сумма.

 

1.                  На чудо яблоне растут бананы и ананасы. За один раз разрешается сорвать с неё два плода. Если сорвать два банана или два ананаса, то вырастет ещё один ананас, а если сорвать один банан и один ананас, то вырастет один банан. В итоге остался один плод. Какой это плод, если известно, сколько бананов и ананасов росло вначале.

 

2.                  На прямой стоят две фишки: слева - красная, справа - синяя. Разрешается производить любую из двух операций: вставку двух фишек одного цвета подряд (между фишками или с краю) и удаление пары соседних одноцветных фишек (между которыми нет других фишек). Можно ли с помощью таких операций оставить на прямой ровно две фишки: слева- синюю, а справа- красную?

3.                  На острове Серобуромалин живут хамелеоны: 13 серых, 15 бурых и 17 малиновых. Если 2 хамелеона разных цветов встречаются, то они оба меняют свой цвет на третий. Может ли случиться, что в не который момент все хамелеоны на острове станут одного цвета?

4.                  По кругу расположены 30 монет, чередуясь: три подряд орлом, три решкой, три орлом, три решкой и т. д. Если у монеты два соседа лежат по-разному, ее можно перевернуть. Какое наибольшее число монет можно положить орлом с помощью таких операций?

5.                  В Зазеркалье имеют хождение монеты достоинством 7, 13 и 25 гиней. Алиса заплатила за пирожок несколько монет, и получила на сдачу на две монеты больше. Какова минимально возможная стоимость покупки?

6.                 На доске написано несколько плюсов и минусов. Разрешается стереть любые два одинаковых знака и написать вместо них плюс или стереть два разных знака и написать минус. Эта операция повторяется, пока на доске не останется один знак. Докажите, что этот последний знак не зависит от порядка и операции.

7.                В стоэтажном небоскрёбе испортился лифт. Теперь в нём работают только две кнопки. При нажатии на первую лифт поднимается на 8 этажей, при нажатии на вторую – опускается на 6 этажей. Можно ли попасть с первого этажа а) на 98-й; б) на 95-й.

8.                На доске написаны числа 1, 2, ..., 101. Разрешается стереть любые два числа и написать вместо них их разность. Так продолжается до тех пор, пока на доске не останется одно число. Может ли это быть 0?

9.               На 44 деревьях, расположенных по кругу, сидели по весёлому чижу.  Время от времени какие-то два чижа перелетают на соседнее дерево - один по часовой стрелке, а другой - против. Могут ли все чижи собраться на одном дереве?

 

 

Полуинвариант. Выбор полуинварианта

 

Пусть есть последовательность объектов, или процесс, в котором позиции последовательно сменяются.

Полуинвариант – это связанное с позицией число, которое при разрешенных действиях все время растет или все время убывает (возможно, нестрого). Выбор полуинварианта зависит от цели.

Если есть строгий полуинвариант, то позиция не может повториться (и, в частности, процесс не может зациклиться). В большинстве игр наличие полуинварианта гарантирует, что игра закончится.

Типичные полуинварианты: сумма, произведение, модуль разности, сумма модулей, сумма квадратов.

Как решать задачи:

В типовых задачах на полуинвариант доказывают невозможность:

а) повторения позиций;

б) бесконечного числа ходов;

в) построения конструкций.

Для последнего находят полуинвариант и проверяют, что для получения искомой конструкции из исходной полуинвариант должен был бы меняться не в ту сторону.

Полуинвариант тоже имеет постоянное при преобразованиях свойство, только он, в отличие от инварианта, величина не постоянная, а монотонно изменяющаяся (увеличивающаяся или уменьшающаяся). Понять присутствие полуинварианта в задаче нам помогает наличие «процесса» в задаче.

Можно использовать инвариант или полуинвариант как для доказательства того, что какое-то условие недостижимо, так и для понимания, какие изменения могут происходить при действиях, описанных в задаче. Если мы обнаружили в задаче уменьшающийся полуинвариант, который может принимать конечное количество значений, то рано или поздно его минимальное значение будет достигнуто. Аналогичная ситуация возникает при увеличивающемся инварианте. Если мы знаем, на сколько за один ход может уменьшаться полуинвариант, мы можем оценить количество ходов, через которое достигается минимум.

 

Раздаточный материал

 

1.                  В колоде 52 карты, по 13 каждой масти. Ваня вынимает из колоды по одной карте.

Вынутые карты в колоду не возвращаются. Каждый раз перед тем, как вынуть карту, Ваня загадывает какую-нибудь масть. Докажите, что если Ваня каждый раз будет загадывать масть, карт которой в колоде осталось не меньше, чем карт любой другой масти, то загаданная масть совпадёт с мастью вынутой карты не менее 13 раз.

2.                  Пьяный библиотекарь каждую минуту снимает с полки какой-то том Британской Энциклопедии, стоящий не на своём месте, и ставит его на своё место (т. е. если номер тома равен k, то он ставит его k-м по счёту). Если в некоторый момент все тома окажутся на своих местах, то библиотекарь запишется в Общество Трезвости. Может ли Общество однозначно рассчитывать на пополнение своих рядов?

3.                  На Архипелаге Сыщик гоняется за Шпионом. Оба используют только маршрутные корабли, которые курсируют ежедневно между некоторыми островами. Каждый корабль отплывает утром и приплывает на остров назначения к вечеру. С пересадками можно добраться с любого острова на любой. Сыщик всегда знает, где сейчас Шпион, и поймает его, если окажется с ним на одном острове. Сыщик может плыть в любой день, Шпион не плавает по пятницам. Как Сыщику поймать Шпиона?

4.                  В десяти сосудах содержится 1, 2, 3,…, 10 литров воды. Разрешается перелить из сосуда А в сосуд В столько воды, сколько имеется в В. Можно ли добиться, чтобы после нескольких переливаний в 5 сосудах оказалось 3 литра, а в остальных 6, 7, 8, 9, 10?

5.                  Двое по очереди ломают шоколадку 6×8. За ход разрешается сделать прямолинейный разлом любого из кусков вдоль углубления. Проигрывает тот, кто не сможет сделать ход. Кто выиграет в этой игре? Подсказка: после каждого хода количество кусков увеличивается ровно на 1.

6.                  На окружности сидят 12 кузнечиков в различных точках.  Эти точки делят окружность на 12 дуг. По сигналу кузнечики одновременно прыгают по часовой стрелке, каждый – из конца своей дуги в ее середину. Образуются новые 12 дуг, прыжки повторяются, и т. д. а) Все кузнечики одновременно вернулись в исходные точки, каждый в свою. Какое наименьшее число прыжков мог сделать каждый кузнечик? б) Может ли хотя бы один кузнечик вернуться в свою исходную точку после того, как им сделано 2 прыжка? в) Как (б), но 13 прыжков?

7.                  В колонию из 2014 бактерий попадает вирус. Каждую секунду каждый вирус уничтожает одну бактерию, после чего каждая бактерия делится на две бактерии, а каждый вирус на два вируса. Докажите, что рано или поздно все бактерии будут уничтожены, и выясните, в какой момент это произойдет.

8.                  В городе живёт 1000 жителей, и у каждого нечётное число врагов. Каждый житель живёт в отдельном доме, и каждый дом окрашен либо в синий, либо в зелёный цвет. В январе первый житель красит свой дом в цвет, отличный от цветов домов большинства его врагов. В феврале это же делает второй житель, и т.д. Докажите, что в некоторый момент цвета домов перестанут меняться.

9.                  Компания производит тамагочи. Каждый день тамагочи мутируют. Если сегодня тамагочи имеет r ручек и n ножек, то назавтра он будет иметь 2r − n ручек и 2n − r ножек. Тамагочи погибает, если число его ручек или ножек становится отрицательным. Докажите, что тамагочи может жить вечно, только если у него число ручек равно числу ножек.

10.              На доске написаны 2014 целых чисел. За ход можно выбрать два числа a и b такие, что a> b+ 2, и заменить из на a −1 и b + 1. Докажите, что в некоторый момент процесс закончится (т.е. больше нельзя будет сделать хода).

11.              На плоскости дано 2014 точек общего положения (т. е. никакие три из них не лежат на одной прямой). Некоторые из них соединены отрезками. Известно, что из любой точки выходит не более 14 отрезков. Докажите, что эти точки можно раскрасить в пять цветов так, чтобы отрезков с одноцветными концами было не более 2014.

12.              На шести гранях кубика написано 6 чисел, среди которых есть 5 и 2014. Каждое из шести чисел одновременно заменили средним арифметическим четырёх чисел, стоящих на соседних гранях. С новыми числами проделали то же самое, и т. д. В некоторый момент на каждой грани оказалось то же самое число, что было вначале. Докажите, что в вычислениях была допущена ошибка.

13.              По окружности расставлены 2014 чисел. Если подряд стоят числа a,b,c,d и при этом (a−d)(b−c)>0,то числа b и c разрешается поменять местами. Докажите, что рано или поздно перестановки прекратятся.

 

 

Схема турнира. Схема подсчета очков. Примеры и контрпримеры.

Принцип Дирихле в заданиях на турниры. Турниры

 

Простейшие понятия, связанные с турнирами: турнирная таблица, системы организации турниров и начисления очков.

Турнир — это в принципе любое соревнование, где количество участников больше двух. Содержание турнира может быть самым разным: футбол, шахматы, решение математических задач и т. д

 

 

 

Схема организации турнира:

·         однокруговые турниры, когда каждый участник встречается с каждым один раз — играет с ним один матч (партию).

·         многокруговые турниры, когда каждая пара участников встречается несколько раз.

Подсчёт очков:

Чаще всего за выигранную партию начисляется 1 очко, за ничью пол-очка ( ½ ) , за проигрыш 0 (шахматная система подсчёта очков).

В некоторых видах соревнований за победу начисляется 2 очка, за ничью 1, за проигрыш 0.

в футболе за выигрыш начисляется 3 очка, за ничью 1, за проигрыш 0.

в волейбольных турнирах, если встреча заканчивается со счетом 3 : 0 или 3 : 1, то выигравшая команда получает 3 очка, а проигравшая 0, если же игра закончилась со счетом 3 : 2, то 2 и 1 очко соответственно.

Турниры по большому. и настольному теннису имеют ту специфику, что в них невозможны ничьи. Бывают и другие схемы организации турниров. В частности, при кубковой, или олимпийской системе турнир состоит из нескольких туров, в каждом из которых участники проводят по одной встрече и проигравший вылетает (если в туре участвует нечётное число спортсменов, то один из них по жребию, отдыхает, и проходит в следующий тур).

Сумма очков, набранных спортсменом во всех партиях, является его результатом. Отдельную партию называют результативной, если она закончилась победой одного из участников, и ничейной в противном случае. Итоги турнира оформляются в виде турнирной таблицы.

Основные виды заданий по турнирам:  восстановить результаты, алгебра турниров

 

 

Раздаточный материал

 

1.      Команда Вымпел во втором матче турнира забросила больше шайб, чем в первом, а в третьем матче — на 6 шайб меньше, чем в двух первых вместе взятых. Известно, что в этих трёх матчах Вымпел забросил 6 шайб. Мог ли Вымпел выиграть все 3 матча?

2.     Аня, Боря, Валя и Гена сыграли однокруговой турнир в крестики-нолики и начали заносить результаты в турнирную таблицу (В — число выигрышей, Н —ничьих, П — поражений). Они успели заполнить только4 клетки (см. рис.). Заполните все остальные клетки.

 

Рассмотрите разные способы восстановления таблицы: перебор вариантов, арифметическое свойство суммы очков по каждой строке.

3.      а) В однокруговом шахматном турнире с восемью участниками все партии

закончились вничью. Сколько всего очков набрали участники? А сколько всего партий

было сыграно?

б) В незаконченном шахматном турнире сыграно пока только 15 партий. Сколько всего очков успели набрать участники?

в) Закончился однокруговой шахматный турнир с 16 участниками. Чему равна сумма набранных очков?

4.      Шахматист сыграл в турнире 20 партий и набрал 12,5 очков. На сколько больше он выиграл партий, чем проиграл?

5.      В однокруговом турнире была применена система подсчёта очков 2–1–0. Вася набрал очков меньше Пети. Может ли у него стать очков больше, чем у Пети, если результаты пересчитать а) по шахматной системе (за победу 1 очко, за ничью ½ , за поражение 0), б) по футбольной системе (за победу 3 очка, за ничью 1,за поражение 0)?

6.      В соревнованиях по олимпийской системе (проигравший выбывает) участвует 47 боксёров. Сколько поединков надо провести, чтобы определить победителя?

7.      На школьном турнире по старой системе подсчета очков за победу в шахматной партии игроку присуждается 1 очко, за ничью — 0,5 очка, за поражение — 0 очков. Известно, что на соревнованиях шахматист набрал 20 очков, сыграв 30 партий. Определите, сколько очков набрал бы этот шахматист, если бы на данных соревнованиях использовалась новая система подсчета очков: за победу — 1 очко, за ничью — 0 очков, за поражение — минус 1 очко (в случае поражения из набранных очков вычитается 1 очко).

8.      В чемпионате России по футболу участвуют 16 команд. Каждая команда играет с каждой по 2 матча. а) Сколько матчей за сезон должен сыграть ярославский "Шинник"? б) Сколько всего матчей играется за один сезон?

9.      Трое друзей играли в шашки. Один из них сыграл 25 игр, а другой – 17 игр. Мог ли третий участник сыграть   а) 34;  б) 35;   в) 56 игр?

10.  Сборная Лихтенштейна по футболу выиграла у сборной Люксембурга со счетом 9:5. Докажите, что по ходу матча был момент, когда сборной Лихтенштейна оставалось забить столько голов, сколько уже забила сборная Люксембурга.

11.  Три шахматиста A, B и C сыграли матч-турнир (каждый с каждым сыграл одинаковое число партий). Может ли случиться, что по числу очков A занял первое место, C – последнее, а по числу побед, наоборот, A занял последнее место, C – первое (за победу присуждается одно очко, за ничью – пол-очка)?

 

 

 Дополнительные задания:

 

Шахматный турнир (1-3)

1.    А) В однокруговом шахматном турнире с 8 участниками все партии закончились вничью. Сколько всего очков набрали участники? А сколько всего партий было сыграно?

Б) В незаконченном шахматном турнире сыграно пока только 17 партий. Сколько всего очков успели набрать участники?

В) Закончился однокруговой шахматный турнир с 16 участниками. Чему равна сумма набранных очков?

Г) Закончился однокруговой турнир 16 команд. Очки считают по старой системе (2-1-0). Чему равна сумма набранных очков? А если бы очки считали по футбольной системе?

2.    Сколько шахматистов играло в однокруговом турнире, если всего в этом соревновании было сыграно 190 партий?

3.    Сколько шахматистов играло в однокруговом турнире, если всего было набрано больше 50, но меньше 60 очков?

Задачи на старую систему подсчета очков (2-1-0) (№№ 4-8)

4.    В однокруговом турнире четырех команд с начислением очков по системе 2-1-0 команда А набрала 5 очков, Б – 2 очка, В – 1 очко. Какое место заняла команда Г?

5.    В розыгрыше приза открытия футбольного сезона в один круг по системе 2-1-0 участвовали пять команд А, Б, В. Г и Д, которые заняли места в том же порядке, начиная с первого. Команда А не сделала ни одной ничьей, команда Б  не проиграла ни одной встречи, команда Г не выиграла ни одной встречи. Все команды набрали разное количество очков. Как окончилась каждая встреча?

6.    В первенстве гимназии по футболу в один круг участвовало 6 команд. Наибольшее число очков в первенстве набрала одна команда. Может ли быть так, что она одержала меньше побед, чем любая другая команда?

7.    В турнире участвовало 6 команд, которые набрали разное число очков. Только один матч закончился вничью. Каждая команда, кроме победительницы, выиграла у одной из занявших более высокое место. Постройте турнирную таблицу.

8.    В первенстве гимназии по футболу в один круг участвовало 6 команд. Наибольшее число очков в первенстве набрала одна команда. Может ли быть так, что она одержала меньше побед, чем любая другая команда?

Футбольная система 3-1-0 (№№ 9-12)

9.    В однокруговом футбольном турнире участвовало 4 команды (А, Б, В, Г). Команда А заняла первое место, а команда Б набрала 3 очка и заняла «чистое» второе место (то есть команда выше нее набрала больше очков, а команда ниже нее – меньше очков). Восстановите результаты всех матчей.

10.                       В футбольном турнире пяти команд победитель набрал столько очков, сколько все остальные вместе взятые. Сколько ничьих было в этом турнире? 

11.                       В однокруговом турнире по футболу участвовали n команд. Сколько партий было сыграно? Какова наибольшая и какова наименьшая возможная сумма очков может быть набрана всеми командами?

12.                       Несколько команд участвуют в однокруговом футбольном турнире. Докажите, что независимо от расписания игр в любой момент найдутся хотя бы две команды, сыгравшие к этому моменту одинаковое количество матчей.

 

Площади

 

Основные понятия: площадь треугольника, площадь трапеции, медиана, высота треугольника, высота трапеции, метод площадей, свойства площадей.

Отношения площадей треугольников:

Если треугольники имеют равные высоты, то отношение их площадей равно отношению их оснований.

Теорема о площадях смежных треугольников:

Если прямая, проведенная из вершины треугольника делит противоположную сторону в отношении m : n, то и площадь треугольника она делит в таком же отношении.

Следствие: Медиана треугольника, проведенная из вершины треугольника, делит треугольник на два равновеликих.

 

 

 

 

 

 

 

 

Раздаточный материал

1. 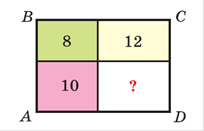     Прямоугольник разбит прямыми, перпендикулярными его сторонам, на четыре части (рис.). Площади трех частей равны 8, 10 и 12. Найдите площадь четвертой (незакрашенной) части прямоугольника. Через точки M и N, делящие сторону AB треугольника ABC на три равные части, проведены прямые, параллельные стороне AC. Найдите площадь части треугольника, заключённой между этими прямыми, если площадь треугольника ABC равна 1.

 

2. 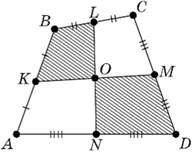      (Обобщение результатов задачи 1) Пусть К, L, М, N – середины сторон АВ, ВС, CD, DA (соот­ветственно) выпуклого четырёхугольника ABCD (см. рис.). Отрезки КМ и LN пересекаются в точке О. До­кажите, что сумма площадей четырёх­угольников AKON и CLOM равна сум­ме площадей    четырёхугольников BKOL и DМОN. 

 

3.      Два равновеликих четырехугольника ABCD и MNPK совместили, как показано на рисунке. Докажите, что сумма площадей зеленых треугольников равна сумме площадей красных треугольников.

 

 

4.      На стороне AB треугольника ABC взяты точки M и N, причём AM  : MN : NB = 2 : 2 : 1, а на стороне AC — точка K, причём AK : KC = 1 : 2. Найдите площадь треугольника MNK, если площадь треугольника ABC равна 1.

5.      Сторону АВ треугольника АВС продолжили за вершину В и выбрали на луче АВ точку А₁ так, что точка В – середина отрезка АА₁. Сторону ВС продолжили за вершину С и отметили на продолжении точку В₁ так, что С – середина ВВ₁. Аналогично, продолжили сторону СА за вершину А и отметили на продолжении точку С₁ так, что А – середина СС₁ . Найдите площадь треугольника А₁В₁С₁, если площадь треугольника АВС равна1.

6.      В треугольнике ABC на стороне АВ взята точка К так, что АК: ВК = 1:2, а на стороне ВС     взята точка L так, что CL: BL = 2:1. Пусть Q – точка пересечения прямых AL и СК. Найдите площадь треугольника ABC, если дано, что площадь треугольника BQC равна 1.

7.      Трапеция разделена диагоналями на четыре треуголь­ника. Площади треугольников, прилегающих к основаниям, равны S1 и S₂. Найдите площадь трапеции с помощью метода площадей.