Программирование  линейных алгоритмов

л инейный а лг оритм — это описание действий, кото- рые выполняются однократно в заданном порядке.

Пример типовой задачи

для заданных a и b вычислить:

ì z = x3 + y3 +10,

ï y = sin (b) - cos(a + x),

ï x =    a +1.

Блок-схема алгоритма

приведена на рис. 1.

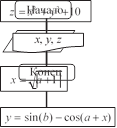рис. 1. блок-схема линейного алгоритма

текст программы на языке Паскаль

program prim1;

var a, b, x, y, z: real; begin

write('введите a='); readln(a); write('введите b='); readln(b);

x  := sqrt(abs(a + 1));

y  := sin(b) – cos(a + x);

z := sqr(x)*x + sqr(y)*y + 10; writeln('x=', x:6:2);

writeln('y=', y:6:2);

writeln('z=', z:6:2)

end.

текст программы на языке С#

using System;

namespace ConsoleApplication18

{

class Program

{

static void Main(string[] args)

{

Console.Write("введите a=");

double a = double.Parse(Console.ReadLine()); Console.Write("введите b=");

double b = double.Parse(Console.ReadLine()); double x = Math.Sqrt(Math.Abs(a + 1)); double y = Math.Sin(b) − Math.Cos(a + x);

double z = Math.Pow(x,3) + Math.Pow(y,3) + 10; Console.WriteLine("x=" + x.ToString("E")); Console.WriteLine("y=" + y.ToString("E")); Console.WriteLine("z=" + z.ToString("E")); Console.ReadLine();

}

}

}

Задачи

1.  известны первый и пятый члены арифметической про- грессии. найти величину члена прогрессии с номером N и сумму N членов.

2.  известны члены арифметической прогрессии с номерами N

и M. найти сумму членов с номерами от M до N (считать M < N).

3.  заданы первый член и знаменатель геометрической про- грессии. найти сумму членов с номерами от заданного номера K до заданного номера P (считать K < P).

4.  повесть рэя брэдбери называется «451 градус по Фарен- гейту». напечатать название повести в градусной мере по цель- сию. Формула перевода:

tC =

5 (t

9   F

- 32).

5.  в классе N учеников. после контрольной работы было получено: А – пятерок, В – четверок, С – двоек, остальные тройки. найти процент троек.

6.  для заданных значений вычислить результат: 1) 1003 - 922 + k;

3) - 5/ 4x + ex/2 ;

6) e-1/2 (x - a);

8)    0, 25(a - b) .

7) ctg (x) - sin (

x2  +1);

1 -         b

8   10n+3 + lg (b)

c - d

7.  заданы x, y, z. вычислить a, b, если:

1)        a =

2             2     ,

1+    +

b = x ëéarctg (z) + e^-(x+3) ùû ;

2)         a =

2      4

3 + ey-1

,

2 cos æ x - p ö

b = 1+ y - x +

z2

( y - x)2

;

2          3

ç  6 ÷

b = 1+          .

3)         a =

è         ø ,                            2

1 + sin2 ( y)                3 + 5

2

8.  для x = –     вычислить значение многочлена по схеме горнера:

z = 5x3 + 70x2 +14x = [(5x + 70)x +14] x.

9.  заданы три числа a, b, c. вычислить их среднее арифмети- ческое:

и среднее геометрическое:

p = a + b + c

3

10.  заданы R, r, h – измерения усеченного конуса. вычислить площадь поверхности и объем усеченного конуса по формулам:

S = p (R + r) l + pR2 + pr 2 ;

V = 1 p (R2 + r 2 + Rr)h; 3

11.  заданы R – радиус окружности и а – сторона правильного вписанного многоугольника. вычислить сторону правильного вписанного многоугольника с удвоенным числом сторон:

b =                                .

12.   заданы a, b, c – стороны треугольника. вычислить радиус вписанной окружности:

r =

и радиус описанной окружности:

R =                 abc                ,

где

p = a + b + c .

2

13.   заданы стороны треугольника a, b, c. вычислить высоту

к стороне а:

h = 2

a         a

p( p - a)( p - b)( p - c);

медиану к стороне а:

биссектрису угла А:

m = 1 2b2 2c2 - a2 ;

a         2

где

b = 2

bcp ( p - a) ,

b + c

p = a + b + c .

2

14. 

где

p = a + b + c .

2

15.  написать программу, вычисляющую расстояние S от

точки с координатами (p, q) до прямой, описываемой уравнением

Ах + Ву + С = 0, по формуле

S =                     .

16.  заданы: r – радиус окружности с центром в точке (0, 0), k – тангенс угла наклона прямой y = kx к оси Ox. вычислить координаты точек пересечения прямой y = kx с окружностью x2 + y2 = r2.

17.  заданы координаты концов отрезка (x1, y2) и (x2, y2) и два целых числа N1, N2. вычислить координаты точки (x, y), которая делит отрезок в отношении N1/N2: если L = N1/N2, то

x = x1 + Lx2 ,

1+ L

y = y1 + Ly2 .

1+ L

18.  найти сумму и произведение цифр заданного трехзнач- ного целого числа K.

19.  задано целое трехзначного число K. найти число, полу- ченное из исходного путем выписывания его цифр в обратном порядке.

20.  плотность железа – 7,9 г/см3, молярная масса – 56 г/моль,

N = 6,02 · 1023. сколько атомов содержится в данном объеме

железа?

21.  написать программу, вычисляющую период колебаний t

маятника длины l по формуле бодного падения (9,81 м/с2).

t = 2p

l /g ,

где g – ускорение сво-

22.  написать    программу,   вычисляющую   силу   притяже-

ния F между телами массы т1 и т2, находящимися на расстоя- нии r друг от друга: F = gт т /r2, где гравитационная постоянная

1     2

g = 6,673 · 10−8 см/г · с2.

23.   написать программу, вычисляющую периметр р правиль- ного n-угольника, описанного около окружности радиуса r по формуле p = 2nr tg (p/n).

24.   написать программу, вычисляющую энергию Е, излу- чаемую черным телом на волне длиной l при температуре Т, по формуле

2pchl-8

E = ech/ BlT -1,

где c = 2,997924 · l08 – скорость света; h = 6,6252 · 10−34 – постоян- ная планка; B = 5,6687 · 10−8 – постоянная больцмана.

Скачано с www.znanio.ru