Программирование разветвлений

р азв етв ляющийся а лг оритм – алгоритм, содержа- щий хотя бы одно условие, в результате проверки которого выпол- няется либо одна, либо другая последовательность действий. выбор направления выполнения алгоритма зависит от исходных или промежуточных данных.

Пример типовой задачи

для заданных a, b и x вычислить:

Блок-схема алгоритма

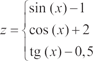приведена на рис. 2.

текст программы на языке Паскаль

program prim2;

var a, b, x, z: real; begin

write('введите a='); readln(a); write('введите b='); readln(b); write('введите x='); readln(x); if x <= a then z: = sin(x) – 1

else

if x >= b then z: = sin(x)/cos(x) – 0.5 else z: = cos(x) + 2;

writeln('z=', z:6:2)

end.

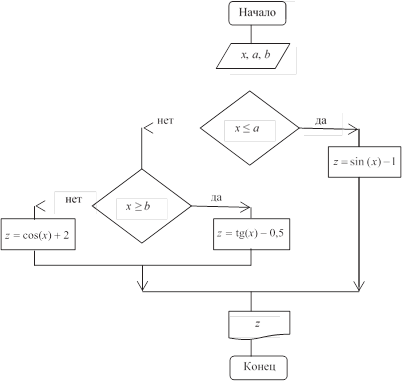
рис. 2. блок-схема разветвляющегося алгоритма

текст программы на языке С#

using System;

namespace ConsoleApplication20

{

class Program

{

static void Main(string[] args)

{

Console.Write("введите a=");

double a = double.Parse(Console.ReadLine()); Console.Write("введите b=");

double b = double.Parse(Console.ReadLine());

Console.Write("введите x=");

double x = double.Parse(Console.ReadLine());

double z;

if (x <= a)

z = Math.Sin(x) – 1; else if (x >= b)

z = Math.Tan(x) – 0.5; else

z = Math.Cos(x) + 2; Console.WriteLine("z=" + z.ToString("E")); Console.ReadLine();

}

}

}

Задачи

1.  ввести целое число N. выяснить, кратно ли оно трем.

2.  по заданным x, y составить программу вычисления значе- ния z:

1) z = min (x, y) + 0,5 ;

1+ max2 (x, y)

3.  даны действительные числа x, y, z. получить:

L = 2max (x, z) – 3min (x, y, z).

4.  по заданным вещественным числам a, b, c вычислить:

P = max (a, b, c) + min (a, b, c) .

2

5.  ввести два целых числа. выяснить, являются ли они оба четными или нечетными, либо одно четное, а другое нечетное.

6.  даны действительные числа a, b, c. проверить, выполня- ются ли неравенства a < b < c.

7.  даны действительные числа a, b, c. удвоить эти числа, если

a ≥ b ≥ c, и заменить их абсолютными значениями, если это не так.

8.  даны два действительных числа. заменить первое число нулем, если оно меньше второго или равно ему, и оставить числа без изменения в противном случае.

9.  даны три действительных числа. выбрать из них те, кото- рые принадлежат интервалу (1, 3).

10.  даны три числа. определить, являются ли они последо- вательными членами арифметической прогрессии, и найти ее разность.

11. 

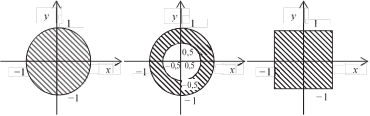а                                       б                                       в

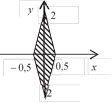
12.  даны действительные числа x, y. определить, принадлежит ли точка с координатами (х, y) заштрихованной части плоскости в вариантах а – в.

у

1

– 2                     1     х

а                                          б                                         в

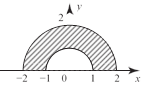
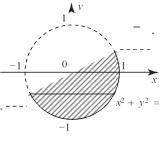
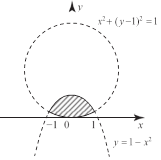
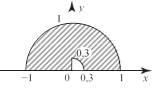
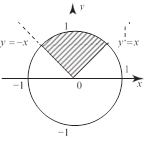
13.  даны действительные числа x, y. определить, принадле- жит ли точка с координатами (х, y) заштрихованной части плос- кости в вариантах а – е.

1

a                                                               б

в                                                                       г

д                                                                  e

14.   заданы целые числа x, y, m, n. если разность (x – y) меньше остатка от деления m на n, увеличить x на 1.

15.   задано целое трехзначное число K. определить, органи- зуют ли цифры этого числа упорядоченную последовательность, и выдать соответствующее сообщение.

16.   по четырехзначному номеру трамвайного билета опреде- лить, является ли он счастливым (билет считается счастливым, если сумма первых двух цифр номера совпадает с суммой двух его последних цифр).

17.  заданы целые числа: k, l, n, m. проверить, является ли k

делителем всех чисел.

18.  заданы размеры А, В прямоугольного отверстия и размеры

x, y, z кирпича. определить, проходит ли кирпич через отверстие.

19.   заданы числа a, b, c. напечатать эти числа в порядке убы- вания их абсолютных величин.

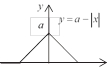
20.  дано действительное число а. для функций f (х), графики которых представлены ниже, вычислить f (a).

y = 0

y = 0     х

y = 0                       х

21.   написать программу для вычисления значения функции f

для заданного значения x:

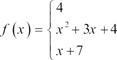22.  заданы числа k, l, m (целые) и x. вычислить величины y(x) и x( y):

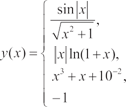
z( y) = y4 – y2 + 5.

23.  выяснить,    попадает     ли     точка     с     координатами (x0, y0)   в    кольцо,    образованное    окружностями    x2 + y2 = r2 и x2 + y2 = R2 (r < R).

24.  определить, в какой координатной четверти находится заданная точка с координатами (x, y).

25.  заданы числа x, y, R. определить расстояние от точки с координатами (x, y) до контура полукруга радиуса R с центром в начале координат, расположенного в нижней полуплоскости.

26.  заданы координаты (x0, y0) точки на плоскости. проверить, лежит ли точка в верхней полуплоскости, и выдать соответствую- щее сообщение.

27.  ввести три вещественных числа a, b, c – длины трех отрез- ков. если отрезки могут быть сторонами треугольника, найти его периметр и площадь.

28.  найти решение системы уравнений:

ì ax + by = c,

ídx + ey = f .

29.   определить, является ли заданный год N високосным. год високосный, если N не кратно 100 и число, изображаемое его двумя последними цифрами, кратно четырем. если N кратно 100, то год високосный лишь при N, кратном 400.

30.  заданы координаты вершин прямоугольника со сторо- нами, параллельными осям координат. определить площадь части прямоугольника, расположенной в первой координатной четверти.

31.  на плоскости заданы точки M1(x1, y1), M2(x2, y2), N1(x3, y3), N2(x4, y4). проверить, являются ли параллельными прямые, одна из которых проходит через точки M1, M2, а другая – через точки N1, N2. если прямые пересекаются, то найти координаты точки пересечения.

32.    два прямоугольника со сторонами, параллельными осям координат, заданы координатами двух своих противоположных вершин: M1(x1, y1), M2(x2, y2) – первый, N1(x3, y3), N2(x4, y4) – второй

прямоугольник. найти площадь их пересечения.

33.   найти координаты точек пересечения прямой y = kx + b и окружности радиуса R с центром в начале координат. опреде- лить, сколько точек пересечения расположены в первой коорди- натной четверти.

34.   заданы числа k, a, b. определить число точек пересечения прямой y = kx + b с гиперболой y = a/x и их координаты.

35.   заданы числа k, a, b. проверить, попадают ли веществен- ные корни уравнения x2 + ax + b = 0 в интервал (−k, k).

36.   заданы числа a, b, x, y, z (a < b). определить, какие из чисел x, y, z попадают в отрезок [a, b]. напечатать также количе- ство таких чисел.

37.  заданы координаты двух точек на плоскости (x1, y1), (x2, y2) и числа R, P (R > 0). определить, попадают ли обе точки внутрь полукруга радиуса R с центром в точке (P, 0), лежащего в верхней

полуплоскости.

38.  заданы числа a, b, c, d (a < b, c < d) и x. определить, при- надлежит ли x какому-либо из отрезков [a, b], [c, d] или их общей части. ответ выдать в виде сообщения.

39.  заданы   числа   k,   b,   c,   d,   e.   определить   количество и координаты точек пересечения прямой у = kx + b и параболы y = cx2 + dx + e и расстояние от каждой точки до начала координат.

40.  заданы числа k, b, a, l. определить, попадают ли обе точки пересечения прямой y = kx + b и параболы y = ax2 в квадрат со стороной l и центром в начале координат (стороны параллельны осям). напечатать сообщение и координаты точек.

41.  заданы числа a, b, c, u, v. найти наибольшее и наименьшее значения функции у = ax2 + bx + c на отрезке [u, v].

42.  составить программу, определяющую число действитель- ных корней биквадратного уравнения ax4 + bx2 + c = 0.

43.  заданы k1, b1, k2, b2 и e (e > 0). определить, содержится ли точка пересечения прямых у = k1х + b1 и у = k2х + b2 в e – окрест- ности начала координат. если прямые совпадают, то проверить

пересечение прямой с e – окрестностью начала координат.

44.  ввести N1, N2, N3 – количества пропущенных часов занятий в среднем на студента за неделю для трех групп. если min (N1, N2, N3) < 10, то напечатать: «есть хорошая группа».

45.  ввести N1, N2, N3 – количества рекламаций на 3 вида

товаров.  напечатать   текст   «все   товары   хорошие»,   если

max (N1, N2, N3) < 5, иначе – «есть плохие товары».

46.  по номеру дня недели выдать сообщение, каким он явля-

ется – рабочим или выходным.