Поделиться
Л2-00486.docx
ц икл со с четчик о м – это циклический алгоритм, в котором тело цикла выполняется заранее известное число раз.
параметр цикла (счетчик) изменяет свое значение от задан- ного начального до заданного конечного, и для каждого значения этой переменной тело цикла выполняется один раз.
Пример типовой задачи
вычислить значения функции y = cos (x) – e x/2 при изменении аргумента х на заданном интервале [c, d ] с заданным шагом h.
приведена на рис. 5.
program prim5;
var с, d, h, x, y: real; m1, m2, i: integer;
begin
write('c='); readln(c);
write('d='); readln(d);
write('h='); readln(h); x := c;
m1 := 1;
m2 := trunc((d – c)/h) + 1; for i := m1 to m2 do
begin
y := cos(x) – exp(x/2); writeln('x=', x:6:2, 'y=', y:6:2 ); x := x+h
end end.
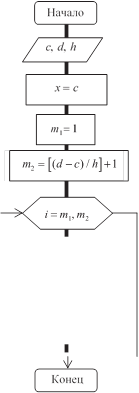
рис. 5. блок-схема алгоритма цикла со счетчиком
using System;
namespace ConsoleApplication23
{
class Program
{
static void Main(string[] args)
{
Console.Write("введите c=");
double c = double.Parse(Console.ReadLine()); Console.Write("введите d=");
double d = double.Parse(Console.ReadLine()); Console.Write("введите h=");
double h = double.Parse(Console.ReadLine()); double y, x = c;
for (int i = 1, m2 = (int)Math.Floor((d–c)/h)+1; i <= m2; ++i) {
y = Math.Cos(x) – Math.Exp(x/2); Console.WriteLine("x={0}, y={1}", x, y); x = x + h;
}
Console.ReadLine();
}
}
}
1. вычислить 10!.
Задачи
2. задана последовательность чисел от 1 до 20. найти сумму квадратов этих чисел.
3. заданы числа x, h, n (n – целое). определить количество тех членов последовательности cos (x), cos (x + h), cos (x + 2h), …, cos (x + nh), которые по абсолютной величине меньше 0,5.
4. заданы числа a, b, h. вычислить сумму значений функции
f (x) =
для x, принадлежащих отрезку [a, b] и изменяющихся с шагом h.
5. вычислить значения многочлена 2a5 – 2a2 – 1,7a + 12 для
а = 0; 1,5; 3; 4,5; 6; 7,5; 9; 10,5.
6. вычислить последовательность значений функции
3x2 - 2
y =
4
для значений аргумента х = 0; 0,05; 0,1; …, 10.
7. составить программу вычисления степени с натуральным показателем y = an, a > 0.
8. составить программу, определяющую, является ли нату- ральное число n простым (число называют простым, если оно делится только на единицу и на себя).
9. автомат отпускает максимум n единиц товара по z рублей за одну единицу и выдает сдачу. у каждого покупателя s рублей. составить программу обслуживания автоматом очереди из k покупателей.
10. необходимо протестировать группу из n человек. каждый из них вводит:
1 – если он изучал английский язык, 2 – если немецкий,
3 – если французский,
0 – если не изучал никакой.
составить программу, определяющую, сколько человек в каждой языковой группе.
11. имеется часть катушки с автобусными билетами. номер билета шестизначный. составить программу, определяющую количество счастливых билетов на катушке, если меньший номер билета – n, больший – m.
12. пусть a0 = 1, ak = kak – 1 + 1/k, k = 1, 2, … . дано натуральное число n. получить an.
13. 
пусть
x0 = c, x1 = d, xk = q xk – 1 +
r xk – 2 + b, k
= 2, 3, … . даны действительные q,
r, b, c,
d и натуральное n (n ³ 2). получить x .
14. пусть u0 = u1 = 1; v0 = v1 = 1;
u = ui -1 - ui - 2vi -1 - vi - 2 ; v =
ui -1 - vi -1
;
i = 3, 4,
¼ .
i 2 2 i
i -1 i -1
дано натуральное число n (n ³ 3). получить vn.
15. пусть
a = a = 1; a = a
+ ai -1 ; i = 2, 3, ¼ .
0 1 i i - 2
2i -1
найти произведение a · a · … · a .
16. пусть
a = b =
1; a
= 1 æ
+ 1 a
ö; b
= 2a2 + b
; k = 2, 3, ¼ .
1 1 k 2 ç
2 k -1 ÷
k k -1
k -1
è ø
 |
åak bk .
k =1
17. пусть x1 = y1 = 1; xi = 0,3 xi – 1; yi = xi – 1 + yi – 1; i = 2, 3, … .
дано натуральное число n. найти
n x
18. пусть
i . i =1 1+ yi
a1 = b1 =
1; ak = 3bk -1 + 2ak -1; bk = 2ak -1 + bk -1;
k = 2, 3, ¼ .
дано натуральное число n. найти
n 2k
å(1+ a2 + 2 ) .
19. пусть a
= u; b
k =1 k
= v; a
bk k !
= 2b + a
; b = 2a2 + b ;
1 1 k
k – 1
k – 1
k k -1
k -1
k = 2, 3, … . даны действительные u, v, натуральное n. найти
n a b
k k . k =1 (k +1)!
20. пусть x1 = x2 = x3 = 1; xi = xi – 1 + xi – 3; i = 4, 5, … . найти
100 x
.
i =1 2i
21. даны натуральное число n, действительное число x.
вычислить:
1)
xn2
2) xn3
2n ;
3n .
22. даны действительные числа a, b (b > a), натуральное число n. получить ( f1 + … + fn) h, где
 |
b - a
ç 2 ÷
h = , fi = è ø , i = 1, 2, ¼, n.
n é æ 1 ö ù2
 |
1+ êa + ç i - 2 ÷ hú
23. вычислить
ë è ø û
1
1+ 1
3 + 1
5 + 1
¼
101+ 1 .
103
24. дано натуральное число n. вычислить 1 · 2 +
+ 2 · 3 · 4 + … + n · (n + 1) · … · 2n.
25. даны целые числа n, k (n ³ k ≥ 0). вычислить
n(n -1) (n - k +1) .
k !
26. пусть n – натуральное число, и пусть n!! означает 1 · 3 · 5 · … · n для нечетного n и 2 · 4 · 6 · … · n для четного n. для заданного натурального n вычислить:
1) n!!;
2) (–1)n + 1 n!!.
27. 
вычислить:
1) å100 1 ;
2) 50 1 ;
3) 10 1;
4) å128 1 .
i =1 i2
i =1 i3
i =1 i!
i =1 (2i)2
28. в окружность радиуса R вписан квадрат. последователь- ным удвоением числа сторон многоугольника получен правиль- ный вписанный в окружность 128-угольник. определить его пери- метр, если сторона многоугольника при удвоении определяется по формуле
a2 N =
29. даны натуральные числа m и n. найти такие натуральные
p и q, не имеющие общих делителей, что p/q=m/n.
30. дано целое n > 2. напечатать простые числа из диапазона [2, n].
31. вычислить
b 1,8 ex
S = ò f (x)dx = ò dx
a 0
по формуле правых прямоугольников с разбиением на N частей:
S » hå
i =1
f (xi ),
h = b - a ,
N
xi = a + ih.
32. вычислить
b 1,8
S = ò f (x)dx = ò
1+ x2 + 0, 4sin (x)dx
a 0
по формуле левых прямоугольников с разбиением на N частей:
N -1
S » h f (xi ),
h = b - a ,
N
xi = a + ih.
i = 0
33. вычислить
b 1,8
S = ò f (x)dx = ò lg 1+ 0, 2x + x2
dx
a 0
по формуле средних прямоугольников с разбиением на N частей:
S » hå
i =1
f (xi ),
h = b - a ,
N
x = a + ih - h .
i 2
34. даны натуральные числа m, n. получить сумму m послед- них цифр числа n.
35. дано натуральное число n. проверить, является ли оно совершенным (число называется совершенным, если оно равно сумме всех своих делителей).
36. получить таблицу температур по цельсию от 0 до 100 гра- дусов и их эквивалентов по шкале Фаренгейта, используя формулу перевода
37. вычислить
t = 9 t
F 5 C
+ 32.
30
2
i i
где
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
