Производная функции. Геометрический и физический смысл производной функции.

Тема: Производная функции.

Геометрический и физический смысл производной функции.

Цели урока:

1. Сформировать понятие производной, скорость изменения функции в точке, а также применение производной к расчету скорости в задачах по физике.

2. Развитие навыков частично-поисковой познавательной деятельности обучающихся; воспитание аккуратности, точности, самостоятельности, привитие навыков групповой работы, сотрудничества.

3. Воспитание у обучающихся интереса к изучаемой теме и ценностного отношения к труду и полученным знаниям.

Тип урока: комбинированный.

Межпредметная связь: математика (средняя скорость изменения функции) – физика (средняя скорость в момент времени).

Ход урока:

1. Орг.момент. Приветствие. Перекличка.

2. Актуализация знаний. Проведение проверочного теста по теме "Графы" (взаимопроверка работ с соседом по парте).

3. Изучение нового материала.

·        Тема урока, цели (на слайде)

·        Историческая справка

·        Определение производной

·        Таблица производных элементарных функций.

·        основные правила дифференцирования.

·        Примеры решения.

·        Тест (закрепление понятия производная)

Введение геометрического смысла

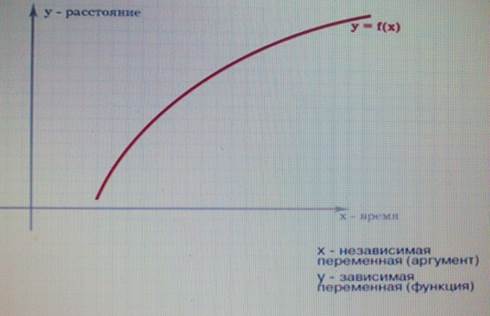
Рис. 1. График функции .

Рассмотрим функцию , ее график и дадим физическую интерпретацию.

Построим систему координат и кривую  (см. рис.1), где

 независимая переменная или аргумент (время),

 – зависимая переменная или функция (расстояние),

 – закон или правило, по которому каждому значению  ставится в соответствие только одно значение .

Зафиксируем момент времени  (см. рис.2). В этот момент времени можно вычислить по заданному закону  , т.е. имеем точку . Эта точка показывает, что в данный момент времени , расстояние -  . Дадим аргументу приращение , т.е. прошло некоторое время . Момент времени, который будет рассматриваться  - это  .

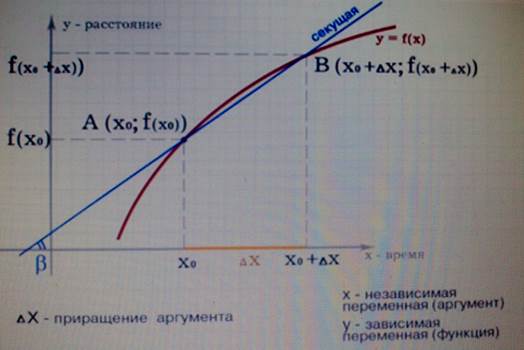
Рис. 2. Секущая к графику функции .

 – приращение аргумента – это разность между новым значением аргумента и старым.

Итак, в новый момент времени, расстояние (от дома) - . Это расстояние можно вычислить по заданному закону, т.е. если подставить в функцию новое значение независимой переменной (аргумента), то можно вычислить новое значение функции. Так получилась точка . В результате получилась секущая , которая наклонена к оси   под углом .

 – секущая,  – ее угол наклона. Этот угол, во – первых, в верхней полуплоскости и, во – вторых, с положительным направлением оси .

Рассмотрим треугольник  (см. рис.3). Он прямоугольный. В этом треугольнике острый угол – это угол -  угол  наклона секущей. Один из катетов - это приращение аргумента, а второй катет – это разность между значением функции в новой точке и значением функции в старой точке.

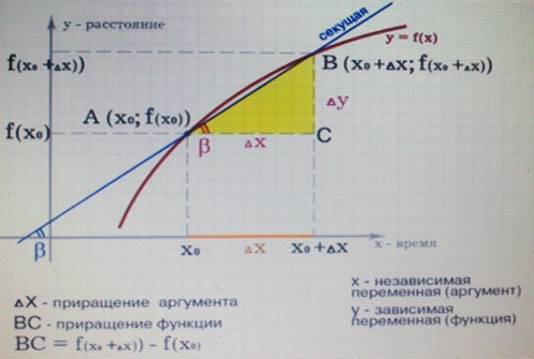
Рис. 3. Приращение функции и приращение аргумента.

Величина  называется  – приращение функции и вычисляется как разность значений функции в новый момент времени минус значение функции в старый момент времени

.

2. Физический смысл отношения ∆f/∆x

Рассмотрим отношение  , где  – приращение функции,  – приращение аргумента (см. рис.4).

Из физических соображений ясно, что отношение расстояния ко времени – это средняя скорость . В этом заключается физический смысл отношения  .

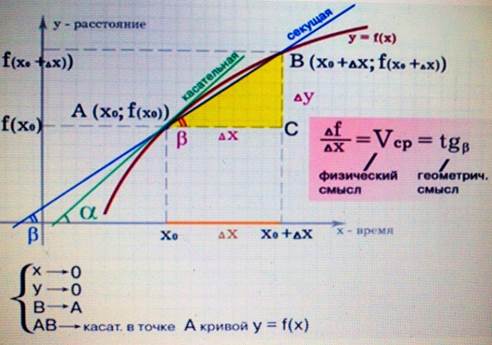
Рис. 4. Физический и геометрический смысл отношения   .

С другой стороны отношение катета  к катету  – это тангенс угла  – тангенс угла наклона секущей, т.е. геометрический смысл отношения   – это тангенс угла наклона секущей  .

3. Определение производной

Пусть . Понятно, что и . Точка  будет стремиться к точке , а положение секущей  будет стремиться занять положение касательной в точке  к кривой   (см. рис.4). Имеем

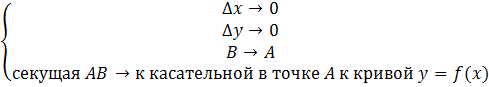
Зафиксируем эту касательную,  – угол наклона этой касательной. Если зафиксировать точку , то отношение   зависит только от величины .

Если отношение    при  стремится к какому-то числу, то это число называется производной функции  в точке  и обозначается .

Определение. Производной функции  в точке  называется число, к которому стремится разностное соотношение    при .

Определение производной с помощью пределов.

Предел при  разностного отношения  , если он существует, называется производной функции в точке  и обозначается .

4. Геометрический и физический смысл производной

, где  – мгновенная скорость в момент . В этом заключается физический смысл производной. Производная – это также тангенс угла наклона касательной , где  - угол наклона касательной к кривой  в точке с абсциссой .

5. Алгоритм нахождения производной

Для того чтобы найти  нужно:

1) Задать приращение  – это приращение аргумента и вычислить соответствующее приращение функции  или .

2) Найти разностное соотношение  , упростить его и сократить на  .

3) Если отношение   при  стремится к какому-то числу, то это число будет .

4. Подведение итогов, дз: § 9.2 - 9.6 , № 9.34 - 9.40

Скачано с www.znanio.ru