Простейшие тригонометрические уравнения. Простейшие тригонометрические неравенства

Простейшие тригонометрические уравнения. Простейшие тригонометрические неравенства

Цели урока:

·           Закрепить основные методы решения простейших тригонометрических уравнений, изучить приемы решения простейших тригонометрических неравенств; 

·           развивать математическую логику и речь; внимание; аккуратность в оформлении записей в тетрадях;

·           воспитать организованность, побуждать учащихся к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.

Ход урока.

1.Организационный момент. Проверка готовности к уроку. Приветствие класса.

Эмоциональный настрой на урок;

2. Мотивация урока. Постановка целей урока.

В алгебре, геометрии, физике и других предметах мы сталкиваемся с разнообразными задачами, решение которых связано с решением уравнений. Мы изучили свойства тригонометрических функций, поэтому естественно обратиться к уравнениям, в которых неизвестное содержится под знаком функций.

Фронтальный опрос:

·         Что такое уравнение?

·         Что значит решить уравнение?

·         Какие уравнения вам знакомы?
Методы их решения.

3. Актуализация опорных знаний. Проверка д/з (сверка с доской № 3, 4 с.323, самопроверка -5 баллов)

Повторить решения простейших тригонометрических уравнений:

       а) проверить работу двух учащихся на доске: решение уравнений вида ,

       б) устно вспомнить решения уравнений вида  

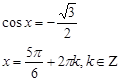Найти ошибки в решениях тригонометрических уравнений:

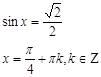
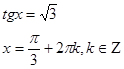
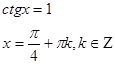
4. Решение простейших тригонометрических уравнений и  уравнений, сводящимся к ним.

Разберем метод подстановки. Методом подстановки решаются те тригонометрические уравнения, которые представляют собой квадратные уравнения относительно какой-либо тригонометрической функции. Если в уравнение входят различные тригонометрические функции, то надо выразить их  через одну.

       а) Разбор учителем уравнения:

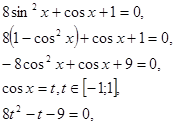        Т.к. 8 – (–1) + (–9)=0, то

       б) Решение уравнения  №2(1), с.345 на доске одним из учеников, остальные работают в тетрадях.

Разберем метод разложения на множители.

       а) Разбор учителем уравнения: №7(4) с.345.

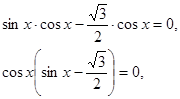
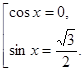
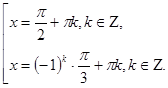
5. Зарядка для глаз.

6. Самостоятельная работа.

Вариант 1 № 1(1), Вариант 2: № 1(3) с.345. Взаимопроверка- 3 балла.

7. Решение простейших тригонометрических неравенств. Просмотр презентации.

Алгоритм решения тригонометрических неравенств с помощью единичной окружности:

1. На оси, соответствующей заданной тригонометрической функции, отметить данное числовое значение этой функции.

2. Провести через отмеченную точку прямую, пересекающую единичную окружность.

3. Выделить точки пересечения прямой и окружности с учетом строгого или нестрогого знака неравенства.

4. Выделить дугу окружности, на которой расположены решения неравенства.

5. Определить значения углов в начальной и конечной точках дуги окружности.

       6. Записать решение неравенства с учетом периодичности заданной тригонометрической функции.

 Работа в группах с таблицей 49.

 8. Закрепление приемов решения простейших тригонометрических неравенств

Решить № 1(1), 2(1), 3(1) с.356.

С/Р. Вариант 1 №1(2), вариант 2- № 2(4) с.356. Самопроверка -2 балла.

9. Итоги урока. Рефлексия. Д\З.

Выучить п. 25, 27,   повторить п. 23, 24, решить № 2(3), 4(1) с.345,  2(4), 3(3) с.356. Буклет по теме.