Простые задачи. Математика. 1 класс

Конотопцева Виктория Николаевна

Учитель начальных классов

МБОУ г. Иркутска гимназия 25

Фрагмент урока по решению простой задачи

УМК «Школа 2100»; Авторы: Т. Е. Демидова, С. А. Козлова, А. П. Тонких

Раздел: Работа с текстовыми задачами.

Тема урока: Задачи на нахождение неизвестного уменьшаемого

Текстовая задача:

·         текст на русском языке, имеющий сюжет, в котором представлены характеристики, отношения, численные компоненты.

·         описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между компонентами или определить вид этого отношения.

Логико-математический анализ задачи:

Вид простой задачи: Нахождение неизвестного уменьшаемого

Задача: На стоянке было несколько машин. Когда 2 машины уехали, осталось 6 машин. Сколько машин было на стоянке сначала?

Компоненты задачи: 2 машин уехало, 6 осталось машин, найти нужно, сколько было изначально машин.

Решение задачи с теоретико-множественного подхода:

Чтобы ответить на вопрос задачи, нужно к уехавшим машинам прибавить оставшиеся машины.
(чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность).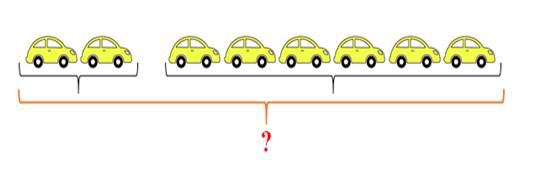

2 + 6 = 8

Ответ: 8 машин было первоначально на стоянке.

Место в системе уроков: начинает изучаться с 1 класса, после идёт расширение понятия. При прохождении данной темы может быть использование как измерительного, так и теоретико-множественного подхода. Могут использоваться в процессе обучения предметные картинки, для наилучшего понимания детей, а также использование схемы, модели по условию задачи, проведение контроля с помощью использования обратных задач, а также вопросы наводящего характера.

Фрагмент урока

Вид работы: Решение простой задачи вида «нахождение неизвестного уменьшаемого».

Дидактическая задача для учителя: Формировать умение решать простые текстовые задачи вида «нахождение неизвестного уменьшаемого».

Учебная задача для учащихся: Сейчас мы с вами будем учиться решать новые текстовые задачи.

Практическая задача для учащихся: Прочитайте задачу.

Организация деятельности: Мы будем решать задачу вместе.
Форма: фронтальная работа

Средства: текст задачи

Метод: словесный - беседа;

            практический - упражнение.

Организация контроля: Контролируйте свои записи в тетради в соответсвии с доской.

Содержательный компонент:

Задача: На стоянке было несколько машин. Когда 2 машины уехали, осталось 6 машин. Сколько машин было на стоянке сначала?

У: О чём наша задача?

Д: Задача о машинах.

У: Что нам известно о них?

Д: Что со стоянки уехало 2 машины и 6 осталось.

У: Что нам неизвестно и что мы должны узнать?

Д: Сколько машин было на стоянке изначально.

У: Правильно. Для того, чтобы узнать, сколько машин было сначала, составим схему. Сколько машин уехало?

Д: 

У: Сколько осталось?

Д:
У: давайте отразим это на схеме.

Д:

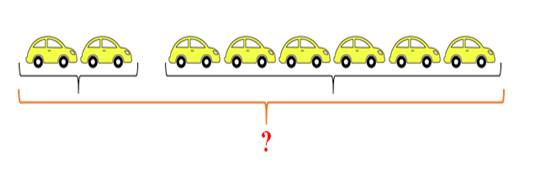
У: Что нужно сделать, чтобы узнать, сколько машин стояло на стояке сначала.

Д: Нужно вернуть эти 2 машины и посчитать, сколько всего их стало.

У: Осталось 6 машин, и мы вернули еще 2 машины. Давайте посчитаем, сколько машин у нас получилось на схеме.

Д: 8

У: Значит, сколько машин было сначала на стоянке?

Д: 8

У: Давайте запишем наш вывод математическим языком. Мы знаем что чтобы узнать сколько было машин сначала, нужно вернуть уехавшие машины к оставшимся. Как это записать?

Д: 2 + 6
У: Правильно. Давайте решим наше выражение.

Д: 2 + 6 = 8

У: Что мы узнали с помощью нашего вычисления.

Д: Сколько машин было изначально.
У: Совпадает ли ответ с тем, что мы посчитали с помощью схемы.

Д: Да.

У: Давайте все равно проверим себя, верно ли мы решили задачу? Давайте составим обратную задачу и решим её. Как она будет звучать?

Д: На стоянке было 8 машин, 2 машины уехали, сколько осталось?

У: Хорошо, а как мы её решим?

Д: Мы должны из 8 машин вычесть уехавшие 2 машины.

У: Правильно. Сколько получится?

Д: 6

У: Значит, верно ли мы решили нашу задачу?

Д: да, ответ совпадает с условием задачи.

У: Давайте запишем ответ нашей задачи.

Д: Ответ: 8 машин было изначально на стоянке.

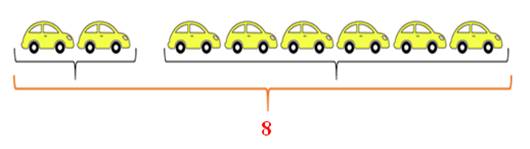
У: Давайте в нашей схеме отобразим решение задачи.

Д: В место вопроса мы ставим 8 машин.

Контрольно-регулировочный компонент: ученики контролируют свою деятельность в соответствии с образцом; учитель использует наводящие вопросы и оценочные суждения.

Оценочно-результативный компонент: Ребята,  мы хорошо с вами поработали, теперь вы научились решать новые текстовые задачи, с помощью которых можно находить неизвестное уменьшаемое.