Прототипы заданий ОГЭ по математике 23

Прототипы задания № 23

№ 338249. По­строй­те гра­фик функ­ции  и опре­де­ли­те, при каких зна­че­ни­ях  пря­мая  имеет с гра­фи­ком не менее одной, но не более трёх общих точек.

Ре­ше­ние.

Рас­кры­вая мо­дуль, по­лу­чим, что функ­цию можно пред­ста­вить сле­ду­ю­щим об­ра­зом:

 

 

 

Этот гра­фик изоб­ражён на ри­сун­ке:

 

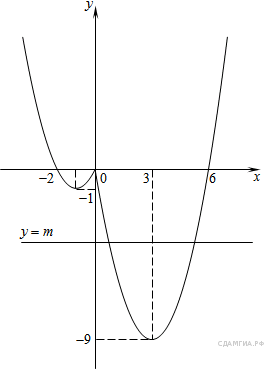
Из гра­фи­ка видно, что пря­мая  имеет с гра­фи­ком функ­ции не менее одной точки пе­ре­се­че­ния при  при­над­ле­жа­щем про­ме­жут­ку 

 

Ответ: 

№ 338288. По­строй­те гра­фик функ­ции  И опре­де­ли­те, при каких зна­че­ни­ях  пря­мая  имеет с гра­фи­ком ровно одну общую точку.

Ре­ше­ние.

Упро­стим вы­ра­же­ние:

 

 

Гра­фик функ­ции сво­дит­ся к гра­фи­ку па­ра­бо­лы  с вы­ко­ло­той точ­кой 

 

Этот гра­фик изоб­ражён на ри­сун­ке:

 

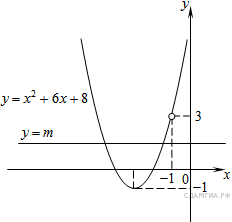
Из гра­фи­ка видно, что пря­мая  имеет с гра­фи­ком функ­ции ровно одну общую точку при  и 

 

Ответ: −1; 3.

№ 314407. При каких зна­че­ни­ях  вер­ши­ны па­ра­бол  ирас­по­ло­же­ны по раз­ные сто­ро­ны от оси ?

Ре­ше­ние.

Ко­ор­ди­на­та  вер­ши­ны па­ра­бо­лы опре­де­ля­ет­ся по фор­му­ле  Ко­ор­ди­на­та  вер­ши­ны на­хо­дит­ся под­ста­нов­кой  в урав­не­ние па­ра­бо­лы. Вер­ши­ны па­ра­бол будут на­хо­дит­ся по раз­ные сто­ро­ны от оси , если ко­ор­ди­на­ты их вер­шин имеют раз­ные знаки. Вспом­нив, что два со­мно­жи­те­ля имеют раз­ный знак тогда и толь­ко тогда, когда их про­из­ве­де­ние от­ри­ца­тель­но, со­ста­вим и решим не­ра­вен­ство:

 

 

За­ме­тим, что пер­вый мно­жи­тель все­гда боль­ше нуля, по­это­му на него можно раз­де­лить.

 

 

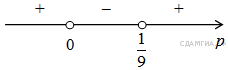
Про­из­ве­де­ние двух со­мно­жи­те­лей будет боль­ше нуля, если со­мно­жи­те­ли имеют оди­на­к­вый знак (см. ри­су­нок). Таким об­ра­зом, по­лу­ча­ем ответ:

 

 

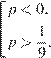
Ответ: 

№ 338249. По­строй­те гра­фик функ­ции  и опре­де­ли­те, при каких зна­че­ни­ях  пря­мая  имеет с гра­фи­ком не менее одной, но не более трёх общих точек.

Ре­ше­ние.

Рас­кры­вая мо­дуль, по­лу­чим, что функ­цию можно пред­ста­вить сле­ду­ю­щим об­ра­зом:

 

 

 

Этот гра­фик изоб­ражён на ри­сун­ке:

 

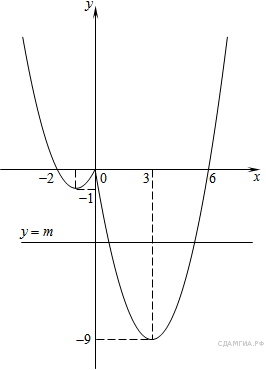
Из гра­фи­ка видно, что пря­мая  имеет с гра­фи­ком функ­ции не менее одной точки пе­ре­се­че­ния при  при­над­ле­жа­щем про­ме­жут­ку 

 

Ответ: 

№ 314801. При каких по­ло­жи­тель­ных зна­че­ни­ях  пря­мая  имеет с па­ра­бо­лой  ровно одну общую точку? Най­ди­те ко­ор­ди­на­ты этой точки и по­строй­те дан­ные гра­фи­ки в одной си­сте­ме ко­ор­ди­нат.

Ре­ше­ние.

Найдём абс­цис­сы точек пе­ре­се­че­ния:

 

 

Гра­фи­ки функ­ций, будут иметь ровно одну точку пе­ре­се­че­ния, если это урав­не­ние имеет ровно одно ре­ше­ние. То есть, если дис­кри­ми­нант этого квад­рат­но­го урав­не­ния будет равен нулю.

 

 

По усло­вию  по­это­му нам под­хо­дит зна­че­ние 

Под­ста­вив па­ра­метр  в урав­не­ние, найдём  ко­ор­ди­на­ту точки пе­ре­се­че­ния этих функ­ций:

 

 

Ко­ор­ди­на­та  на­хо­дит­ся путём под­ста­нов­ки ко­ор­ди­на­ты  в любое из урав­не­ний, на­при­мер, в пер­вое:

 

 

Те­перь, зная  можем по­стро­ить гра­фи­ки обеих функ­ций (см. ри­су­нок).

 

 

 

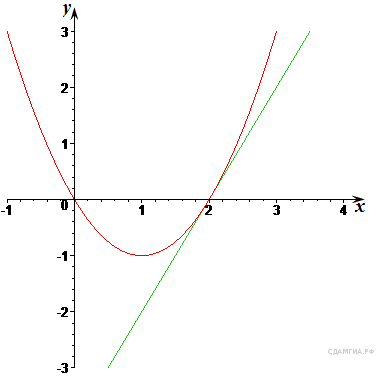
Ответ: (2; 0).

№ 314446. При каких зна­че­ни­ях  вер­ши­ны па­ра­бол  и  рас­по­ло­же­ны по одну сто­ро­ну от оси ?

Ре­ше­ние.

Ко­ор­ди­на­та  вер­ши­ны па­ра­бо­лы опре­де­ля­ет­ся по фор­му­ле  Ко­ор­ди­на­та  вер­ши­ны на­хо­дит­ся под­ста­нов­кой  в урав­не­ние па­ра­бо­лы. Вер­ши­ны па­ра­бол будут на­хо­дит­ся по одну сто­ро­ну от оси , если ко­ор­ди­на­ты их вер­шин имеют оди­на­ко­вые знаки. Вспом­нив, что два со­мно­жи­те­ля имеют оди­на­ко­вый знак тогда и толь­ко тогда, когда их про­из­ве­де­ние по­ло­жи­тель­но, со­ста­вим и решим не­ра­вен­ство:

 

 

За­ме­тим, что вто­рой мно­жи­тель все­гда боль­ше нуля, по­это­му на него можно раз­де­лить.

 

 

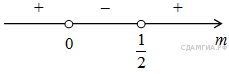
Про­из­ве­де­ние двух со­мно­жи­те­лей будет мень­ше нуля, если со­мно­жи­те­ли имеют раз­ный знак (см. ри­су­нок). Таким об­ра­зом, по­лу­ча­ем ответ:

 

 

Ответ: 

№ 314727. Из­вест­но, что гра­фи­ки функ­ций  и  имеют ровно одну общую точку. Опре­де­ли­те ко­ор­ди­на­ты этой точки. По­строй­те гра­фи­ки за­дан­ных функ­ций в одной си­сте­ме ко­ор­ди­нат.

Ре­ше­ние.

Найдём абс­цис­сы точек пе­ре­се­че­ния:

 

 

Гра­фи­ки функ­ций, будут иметь ровно одну точку пе­ре­се­че­ния, если это урав­не­ние имеет ровно одно ре­ше­ние. То есть, если дис­кри­ми­нант этого квад­рат­но­го урав­не­ния будет равен нулю.

 

 

Под­ста­вив па­ра­метр  в урав­не­ние, найдём  ко­ор­ди­на­ту точки пе­ре­се­че­ния этих функ­ций:

 

 

Ко­ор­ди­на­та  на­хо­дит­ся путём под­ста­нов­ки ко­ор­ди­на­ты  в любое из урав­не­ний, на­при­мер, во вто­рое:

 

 

Те­перь, зная  можем по­стро­ить гра­фи­ки обеих функ­ций (см. ри­су­нок).

 

 

 

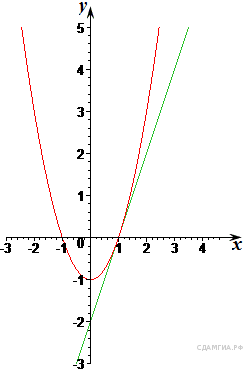
Ответ: (1; 0).

№ 314715. По­строй­те гра­фик функ­ции  и опре­де­ли­те, при каких зна­че­ни­ях  пря­мая  имеет с гра­фи­ком ровно три общие точки.

Ре­ше­ние.

Рас­кры­вая мо­дуль, по­лу­чим, что гра­фик функ­ции можно пред­ста­вить сле­ду­ю­щим об­ра­зом:

 

 

Этот гра­фик изоб­ражён на ри­сун­ке:

 

 

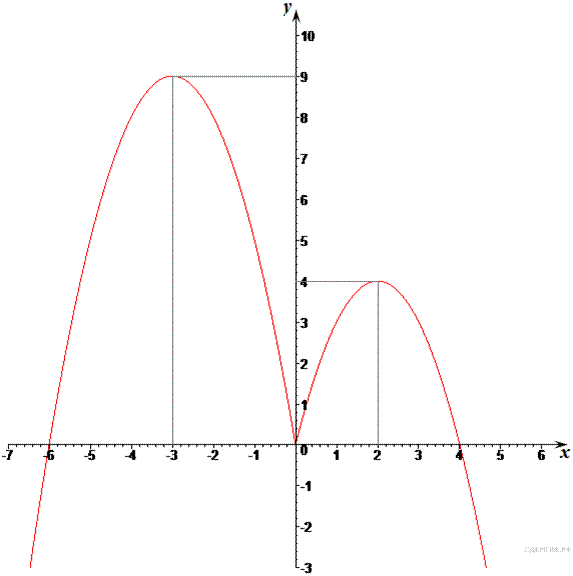
Из гра­фи­ка видно, что пря­мая  имеет с гра­фи­ком функ­ции ровно три общие точки при  и 

 

Ответ: 0; 4.

№ 314409. Па­ра­бо­ла про­хо­дит через точки A(0; 6), B(6; –6), C(1; 9). Най­ди­те ко­ор­ди­на­ты её вер­ши­ны.

Ре­ше­ние.

Одна из воз­мож­ных форм за­пи­си урав­не­ния па­ра­бо­лы в общем виде вы­гля­дит так:  Ко­ор­ди­на­та  вер­ши­ны па­ра­бо­лы на­хо­дит­ся по фор­му­ле  Ко­ор­ди­на­ту вер­ши­ны па­ра­бо­лы найдётся под­ста­нов­кой  в урав­не­ние па­ра­бо­лы. Таким об­ра­зом, за­да­ча сво­дит­ся к на­хож­де­нию ко­эф­фи­ци­ен­тов  и  Под­ста­вив ко­ор­ди­на­ты точек, через ко­то­рые про­хо­дит па­ра­бо­ла, в урав­не­ние па­ра­бо­лы и по­лу­чим си­сте­му из трёх урав­не­ний:

 

 

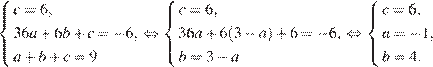
Найдём ко­ор­ди­на­ты вер­ши­ны:

 

 

Ответ: (2; 10).

№ 338207. По­строй­те гра­фик функ­ции  и опре­де­ли­те, при каких зна­че­ни­ях  пря­мая  имеет с гра­фи­ком ровно две общие точки.

Ре­ше­ние.

Упро­стим вы­ра­же­ние:

 

 

Таким об­ра­зом, по­лу­чи­ли, что гра­фик нашей функ­ции сво­дит­ся к гра­фи­ку функ­ции  с вы­ко­ло­тыми точ­ками  и  По­стро­им гра­фик функ­ции (см. ри­су­нок).

 

Этот гра­фик изоб­ражён на ри­сун­ке:

 

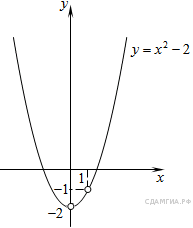
Из гра­фи­ка видно, что пря­мая  имеет с гра­фи­ком функ­ции ровно две общие точки при  при­над­ле­жа­щем про­ме­жут­ку 

 

Ответ: 

№ 314761. По­строй­те гра­фик функ­ции

 

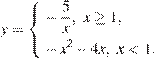
и опре­де­ли­те, при каких зна­че­ни­ях  пря­мая  будет пе­ре­се­кать по­стро­ен­ный гра­фик в трёх точ­ках.

Ре­ше­ние.

По­стро­им гра­фик функ­ции (см. ри­су­нок).

 

 

 

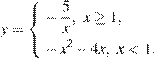
Из гра­фи­ка видно, что пря­мая  будет иметь с гра­фи­ком функ­ции ровно три точки пе­ре­се­че­ния при  при­над­ле­жа­щем мно­же­ству: 

 

Ответ: (−5; 0).

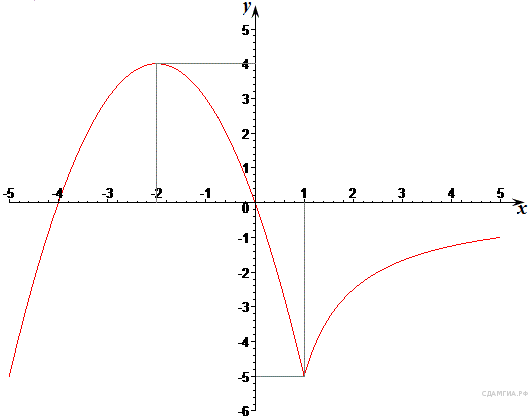
№ 333156. По­строй­те гра­фик функ­ции

 

и опре­де­ли­те, при каких зна­че­ни­ях m пря­мая y = m имеет с гра­фи­ком ровно две общие точки.

Ре­ше­ние.

По­стро­им гра­фик функ­ции  при  и гра­фик функ­ции  при 

Пря­мая  имеет с гра­фи­ком ровно две общие точки при  и 

 

Ответ: −3; −2.