Прототипы задания № 18 ОГЭ математика 2018-2019 уч.год

Пло­ща­ди фигур

1. 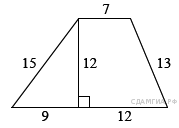Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

 

2. 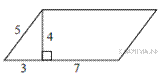Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

 

3. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.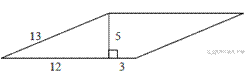

 

4. 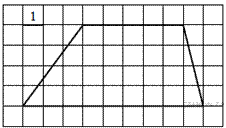Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

 

5. 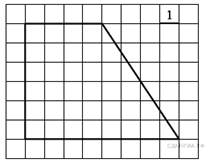Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

 

6. 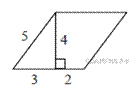Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

 

7. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, а угол, ле­жа­щий на­про­тив него, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

8. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, а ост­рый угол, при­ле­жа­щий к нему, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

9. Сто­ро­на рав­но­сто­рон­не­го тре­уголь­ни­ка равна 10. Най­ди­те его пло­щадь, делённую на

 

10. Пе­ри­метр рав­но­сто­рон­не­го тре­уголь­ни­ка равен 30. Най­ди­те его пло­щадь, делённую на .

11. Вы­со­та рав­но­сто­рон­не­го тре­уголь­ни­ка равна 10. Най­ди­те его пло­щадь, делённую на

12. В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 120°. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на

13. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 16, а бо­ко­вая сто­ро­на — 5. Най­ди­те пло­щадь тре­уголь­ни­ка.

14. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 16, а ос­но­ва­ние — 6. Най­ди­те пло­щадь тре­уголь­ни­ка.

15. В тре­уголь­ни­ке одна из сто­рон равна 10, а опу­щен­ная на нее вы­со­та — 5. Най­ди­те пло­щадь тре­уголь­ни­ка.

16. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 60°. Най­ди­те пло­щадь тре­уголь­ни­ка.

17. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

18. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 120°. Най­ди­те пло­щадь тре­уголь­ни­ка.

19. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 135°. Най­ди­те пло­щадь тре­уголь­ни­ка.

20. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна 12, а угол между ними равен 30°. Най­ди­те пло­щадь тре­уголь­ни­ка.

21. В тре­уголь­ни­ке одна из сто­рон равна 12, дру­гая равна 16, а синус угла между ними равен . Най­ди­те пло­щадь тре­уголь­ни­ка.

22. В тре­уголь­ни­ке одна из сто­рон равна 12, дру­гая равна 10, а ко­си­нус угла между ними равен . Най­ди­те пло­щадь тре­уголь­ни­ка.

23. Сто­ро­на квад­ра­та равна 10. Най­ди­те его пло­щадь.

24. Пе­ри­метр квад­ра­та равен 40. Най­ди­те пло­щадь квад­ра­та.

25. В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сто­ро­на равна 12. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

26. В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, пе­ри­метр равен 44. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

27. В пря­мо­уголь­ни­ке одна сто­ро­на равна 6, а диа­го­наль равна 10. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

28.. В пря­мо­уголь­ни­ке диа­го­наль равна 10, а угол между ней и одной из сто­рон равен 30°. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, делённую на .

29. Сто­ро­на ромба равна 5, а диа­го­наль равна 6. Най­ди­те пло­щадь ромба.

30. Пе­ри­метр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

31. Пе­ри­метр ромба равен 40, а один из углов равен 45°. Най­ди­те пло­щадь ромба, делённую на .

 

32. Пе­ри­метр ромба равен 40, а один из углов равен 60°. Най­ди­те пло­щадь ромба, делённую на

33. Пе­ри­метр ромба равен 24, а синус од­но­го из углов равен . Най­ди­те пло­щадь ромба.

 

34. Пе­ри­метр ромба равен 24, а ко­си­нус од­но­го из углов равен . Най­ди­те пло­щадь ромба.

 

35. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

36. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, дру­гая равна 5, а один из углов — 45°. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, делённую на .

37. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, дру­гая равна 5, а один из углов — 60°. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, делённую на .

38. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, дру­гая равна 5, а синус од­но­го из углов равен . Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

39. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, дру­гая равна 5, а ко­си­нус од­но­го из углов равен . Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

 

40. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, дру­гая равна 5, а тан­генс од­но­го из углов равен . Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

41. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна , а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те пло­щадь тра­пе­ции.

 

42.Ос­но­ва­ния тра­пе­ции равны 18 и 10, одна из бо­ко­вых сто­рон равна , а угол между ней и одним из ос­но­ва­ний равен 120°. Най­ди­те пло­щадь тра­пе­ции.

 

43. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те пло­щадь тра­пе­ции.

 

44. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те пло­щадь тра­пе­ции.

 

45.Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а тан­генс угла между ней и одним из ос­но­ва­ний равен . Най­ди­те пло­щадь тра­пе­ции.

 

46. Ра­ди­ус круга равен 1. Най­ди­те его пло­щадь, де­лен­ную на π.

 

47. Най­ди­те пло­щадь кру­го­во­го сек­то­ра, если ра­ди­ус круга равен 3, а угол сек­то­ра равен 120°. В от­ве­те ука­жи­те пло­щадь, де­лен­ную на π.

 

48. Най­ди­те пло­щадь кру­го­во­го сек­то­ра, если длина огра­ни­чи­ва­ю­щей его дуги равна 6π, а угол сек­то­ра равен 120°. В от­ве­те ука­жи­те пло­щадь, де­лен­ную на π.

 

49. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, ост­рый угол, при­ле­жа­щий к нему, равен 60°, а ги­по­те­ну­за равна 20. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на .

 

50. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен , ост­рый угол, при­ле­жа­щий к нему, равен 30°, а ги­по­те­ну­за равна 20. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на .

 

 

51. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, угол, ле­жа­щий на­про­тив него, равен 30°, а ги­по­те­ну­за равна 20. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на .

52. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен , угол, ле­жа­щий на­про­тив него, равен 60°, а ги­по­те­ну­за равна 20. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на .

53. В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, ос­но­ва­ние — , а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 30°. Най­ди­те пло­щадь тре­уголь­ни­ка.

54. В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, ос­но­ва­ние — , а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка, де­лен­ную на

55. В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, ос­но­ва­ние — , а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 120°. Най­ди­те пло­щадь тре­уголь­ни­ка, де­лен­ную на

56. В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, ос­но­ва­ние — , а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 135°. Най­ди­те пло­щадь тре­уголь­ни­ка, де­лен­ную на

 

57. В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, ос­но­ва­ние — , а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 150°. Най­ди­те пло­щадь тре­уголь­ни­ка.

 

58. В пря­мо­уголь­ни­ке диа­го­наль равна 10, угол между ней и одной из сто­рон равен 30°, длина этой сто­ро­ны . Най­ди­те пло­щадь пря­мо­уголь­ни­ка, де­лен­ную на

 

59. В пря­мо­уголь­ни­ке диа­го­наль равна 10, а угол между ней и одной из сто­рон равен 60°, длина этой сто­ро­ны равна 5. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, де­лен­ную на

 

60. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 30°. Най­ди­те пло­щадь ромба.

61. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 45°. Най­ди­те пло­щадь ромба, де­лен­ную на

 

62. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 120°. Най­ди­те пло­щадь ромба, де­лен­ную на

 

63. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — 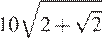, а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 135°. Най­ди­те пло­щадь ромба, де­лен­ную на

 

64. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 150°. Най­ди­те пло­щадь ромба.

 

65. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — 10, а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 60°. Най­ди­те пло­щадь ромба, де­лен­ную на

 

66. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 150°. Най­ди­те пло­щадь ромба.

Ответ: 50

 

67. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 60°. Най­ди­те пло­щадь ромба, де­лен­ную на

 

68. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — 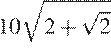, а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 45°. Най­ди­те пло­щадь ромба, де­лен­ную на

69. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 30°. Най­ди­те пло­щадь ромба.

Ответ: 50

 

70. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — 10, а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 120°. Най­ди­те пло­щадь ромба, де­лен­ную на

 

71. Ра­ди­ус круга равен 3, а длина огра­ни­чи­ва­ю­щей его окруж­но­сти равна 6π. Най­ди­те пло­щадь круга. В ответ за­пи­ши­те пло­щадь, де­лен­ную на π.

72.  Най­ди­те пло­щадь кру­го­во­го сек­то­ра, если длина огра­ни­чи­ва­ю­щей его дуги равна 6π, угол сек­то­ра равен 120°, а ра­ди­ус круга равен 9. В ответ ука­жи­те число, де­лен­ную на π.

 

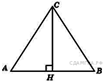
73. В рав­но­бед­рен­ном тре­уголь­ни­ке . Най­ди­те , если вы­со­та .

 

74. В рав­но­бед­рен­ном тре­уголь­ни­ке  . Най­ди­те  , если вы­со­та  .

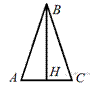
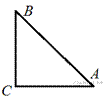
75. В тре­уголь­ни­ке    угол    равен 90°,  . Най­ди­те  .

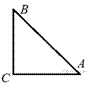
76. В тре­уголь­ни­ке    угол    равен 90°,  .  Най­ди­те  .

77. Ос­но­ва­ния тра­пе­ции равны 4 см и 10 см. Диа­го­наль тра­пе­ции делит сред­нюю линию на два от­рез­ка. Най­ди­те длину боль­ше­го из них.

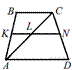
78. Диа­го­наль тра­пе­ции делит её сред­нюю линию на от­рез­ки, рав­ные 4 см и 3 см. Най­ди­те мень­шее ос­но­ва­ние тра­пе­ции.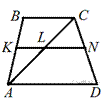

 

79. Сред­няя линия тра­пе­ции равна 11, а мень­ше ос­но­ва­ние равно 5. Най­ди­те боль­шее ос­но­ва­ние тра­пе­ции.

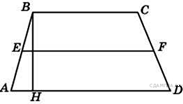
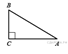
80. В тре­уголь­ни­ке    угол    пря­мой,  . Най­ди­те  .

81. 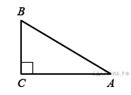В тре­уголь­ни­ке    угол    пря­мой,  . Най­ди­те  .

 

82. 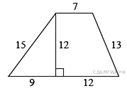Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

 

83. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 44 и одна сто­ро­на на 2 боль­ше дру­гой.

 

84. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 60, а от­но­ше­ние со­сед­них сто­рон равно 4:11.

 

85. 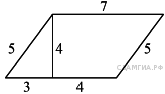Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

 

86. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

 

87. 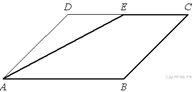Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 56. Точка E — се­ре­ди­на сто­ро­ны CD. Най­ди­те пло­щадь тра­пе­ции AECB.

 

88. 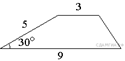Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

 

89.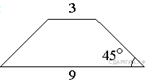В рав­но­бед­рен­ной тра­пе­ции ос­но­ва­ния равны 3 и 9, а один из углов между бо­ко­вой сто­ро­ной и ос­но­ва­ни­ем равен 45°. Най­ди­те пло­щадь тра­пе­ции.

 

90. 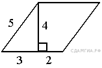Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

 

91. 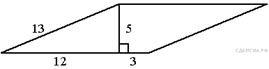Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

92. 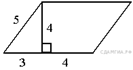Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

 

93. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 92, а от­но­ше­ние со­сед­них сто­рон равно 3:20.

 

94. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 58 и одна сто­ро­на на 5 боль­ше дру­гой.

 

95. 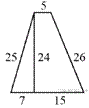Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

 

96. 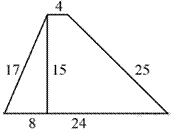Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

 

97. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, а угол, ле­жа­щий на­про­тив него равен 45∘. Най­ди­те пло­щадь тре­уголь­ни­ка.

98. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 392, а ос­но­ва­ние – 192. Най­ди­те пло­щадь тре­уголь­ни­ка.