Рабочая программа элективного курса по математике "Нестандартные способы решения уравнений и неравенств"

 

Муниципальное бюджетное общеобразовательное учреждение Мучкапская средняя общеобразовательная школа

 

 

 

 

 

 

 

 

 

 

Рабочая программа

Учебной элективной дисциплины

« Нестандартные методы решения

уравнений и неравенств»

для 9-11 классов

общеобразовательной школы

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Р.п. Мучкапский

 

2017г

Рабочая программа учебной элективной дисциплины

«Нестандартные методы решения уравнений и неравенств»

для 9 – 11 классов общеобразовательной школы.

 

 Пояснительная записка.

         Государственной программой изучения математики в 9 – 11 классах предусматривается изучение стандартных методов решения уравнений и неравенств, однако, на практике при сдаче единого государственного экзамена, при поступлении в различные учебные заведения, при выполнении  олимпиадных заданий, а также при участии в рейтинговом тестировании в вузах часто приходится решать такие упражнения, где стандартные методы решения заводят в тупик или приводят к очень длинному запутанному решению. Для решения таких задач лучше применять приёмы, которые не совсем привычны для учащихся.

        При разработке предлагаемой программы преследовалась цель:       познакомить учащихся с различными методами решения, основанными на материале программы общеобразовательной средней школы, казалось бы, трудных задач, проиллюстрировать широкие возможности использования хорошо усвоенных школьных знаний, привить навыки употребления нестандартных методов рассуждения при решении задач.

        Изучение элективного курса «Нестандартные методы решения уравнений и неравенств» в 9 – 11 классах общеобразовательной школы направлено на достижение следующих задач:

·        познакомить учащихся с методами решения уравнений и неравенств,     основанными на геометрических воображениях, свойствах функций (монотонность, ограниченность, чётность), применении производной и т.д.                         

·         научить применять эти методы при решении;

·         привить умение выбирать наиболее рациональный метод при решении конкретной задачи;

·        развить умение приобретённые навыки использовать при выполнении домашних заданий, при решении задач подготовительных курсов при вузах, при решении олимпиадных заданий, при сдаче ЕГЭ.

Программа предусматривает поурочную форму обучения.

Итоговой формой контроля является зачёт.

Программа рассчитана на 85 часов (9 класс – 17 часов, 10 класс – 34 часа,  11 класс – 34 часа).

 

 

 

 

 

Содержание программы

9 класс (17 часов)

I.            Разложение на множители (5 часов)

          Вынесение общего множителя. Применение формул сокращенного умножения. Группировка. Метод неопределенных коэффициентов.

Подбор корня многочлена по его старшему и свободному коэффициенту.

Метод введения параметра. Метод введения новой переменной. Комбинирование различных методов. 

II.            Алгебраические уравнения (6 часов)

Простейшие способы решения уравнений. Симметрические уравнения третьей              степени, четвертой степени. Возвратные уравнения. Умножение уравнения на функцию. Угадывание корня уравнений.

III.            Системы нелинейных уравнений (3 часа)

Простейшие способы решения систем. Способ введения новых переменных. Комбинирование различных методов.

IV.            Решение алгебраических неравенств (3 часа)

Простейшие способы решения неравенств. Метод интервалов, Обобщенный метод интервалов.

                                             10 класс (34 часа)

I.      Алгебраические уравнения (4 часа)

Понижение степени уравнения.

Решение уравнений вида: (х+α)⁴ + (х+β)⁴ = С

                                             (х-α) (х-β) (х-γ) (х-δ) = А

II.      Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины (8 часов)

Раскрытие знаков модулей

Уравнения вида   

Неравенства вида

Неравенства вида

Уравнения и неравенства вида ,

Использование свойств абсолютной величины.

III.      Рациональные уравнения (6 часов)

Упрощение уравнения

Уравнения вида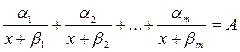

                            

                            

                           

 

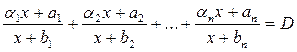
IV.      Решение тригонометрических уравнений (6 часов)

Простейшие способы решений уравнений. Последовательность отбора корней уравнения. Геометрический, арифметический и алгебраические способы отбора корней. Тригонометрические уравнения, содержащие знак абсолютной величины.

V.      Решение уравнений с использованием свойств, входящих в них функций  (6 часов)

Использование ОДЗ. Использование ограничений функций. Использование монотонности функций. Использование графиков функций. Использование свойств синуса и косинуса.

VI.      Итоговое повторение (4 часа)

 

11 класс (34 часа)

 

I.      Решение уравнений с параметрами (5 часов)

Решение линейных уравнений с параметрами. Решение квадратных уравнений с параметрами. Существование корней трехчлена второй степени с параметрами, выявление их количеств. Расположение корней на числовой прямой относительно заданных точек, промежутков.

II.      Решение уравнений и неравенств, содержащих радикалы (5 часов) Возведение в степень.

Уравнения вида

Умножение уравнения на функцию.

Уравнение вида 

Уравнение вида  

III.      Решение некоторых уравнений и неравенств,  сведением их к решению систем уравнений или неравенств относительно той же неизвестной

  (6 часов)

Уравнения вида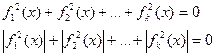  

Неравенства вида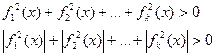

Использование ограниченности функции.

IV.      Применение производной (5 часов)

Использование монотонности функции. Использование наибольшего и наименьшего значений функций. Применение теоремы  Лагранжа.

V.      Уравнения и неравенства, содержащие логарифмы (8 часов)

Переход к числовому основанию. Переход к основанию, содержащему неизвестную.

Уравнения вида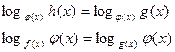

Уравнения вида

Неравенства  вида

Уравнения и неравенства, содержащие неизвестную в основании и показателе степени.

 

VI.      Итоговое повторение (5 часов)

 

Требования к уровню

подготовки учащихся.

    В результате изучения элективной дисциплины ученик должен

знать

*эвристические приёмы общего характера, применяемые в исследованиях и на любом другом математическом материале, ценные для математического развития личности;

* значение, широту и в то же время ограниченность применения различных    математических методов к анализу и исследованию процессов явлений, происходящих в окружающей действительности;

* значение практики для формирования и развития математических знаний;

* универсальный характер законов логики математических рассуждений, их применяемость во всех областях человеческой деятельности;

уметь

*   раскладывать многочлен на множители различными способами и

применять это при решении уравнений, неравенств и их систем

повышенного уровня;  

*   решать  рациональные, показательные, логарифмические,                           иррациональные и тригонометрические уравнения, неравенства и        

их системы повышенного уровня;                                                                                                          *   решать уравнения, неравенства и системы повышенного уровня с                                

применением  графических представлений, свойств функций,

производной;

*   решать уравнения и неравенства, содержащих неизвестную под знаком абсолютной величины;

*   решать уравнения с параметрами.

Тематическое планирование

 

№ урока	Тема урока	Кол-во часов
9 класс
Тема №1 «Разложение на множители» (5 часов)
1.	Вынесение общего множители. Применение формул сокращённого умножения. Группировка.	1
2.	Метод неопределённых коэффициентов. Подбор корня многочлена по его старшему и свободному коэффициентам.	1
3.	Метод параметра. Метод введения новой переменной. Комбинирование различных методов.	1
4-5.	Занятия-практикумы на закрепление теоретического материала	2
Тема №2 « Алгебраические уравнения» (6 часов)
6.	Простейшие способы решения уравнений	1
7.	Симметричные уравнения третьей степени, четвёртой степени	1
8.	Возвратные уравнения. Угадывание корня уравнения.	1
9.	Умножение уравнения на функцию.	1
10-11.	Занятия-практикумы на закрепление теоретического материала по теме.	2
Тема №3 « Системы нелинейных уравнений» ( 3 часа)
12.	Простейшие способы решения систем. Способ введения новых переменных.	1
13.	Комбинирование различных способов.	1
14.	Урок-практикум.	1
Тема №4 « Решение алгебраических неравенств» (3 часа)
15.	Простейшие способы решения неравенств	1
16.	Метод интервалов. Обобщённый метод интервалов	1
17.	Зачёт	1
10 класс (34 часа)
Тема №1 « Алгебраические уравнения» (4 часа)
1.	Понижение степени уравнения	1
2.	Решение уравнения вида (х +ά ) + ( х +β ) = С	1
3.	Решение уравнений вида (х -α ) ( х -β ) ( х -γ) ( х -δ ) = А	1
4.	Урок-практикум.	1
Тема №2 « Уравнении и неравенства, содержащие неизвестную под знаком абсолютной величины» ( 8 часов)
5.	Раскрытие знаков модулей	1
6.	Уравнения вида | f(х)| = g(х), | f(х)| = |g(х)|	1
7.	Неравенства вида | f(х)| < g(х), | f(х)| > g(х)	1
8.	Неравенство вида | f(х)| < |g(х)|	1
9.	Уравнения вида | f(х)| + |g(х)| = h(х)	1
10.	Использование свойств абсолютной величины	1
11-12	Занятия-практикумы по закреплению теоретического материала темы	2
Тема №3 «Рациональные уравнения» (6 часов)
13.	Упрощение уравнения	1
15.	Уравнения вида =А, .	1
16.	Уравнения вида	1
17.	Уравнение вида	1
18-19	Занятия-практикумы по закреплению теоретического материала темы.	2
Тема №4 « Решение тригонометрических уравнений»(6 часов)
20.	Простейшие способы решений тригонометрических уравнений.	1
21.	Последовательность отбора корней уравнения.	1
22.	Геометрический, арифметический и алгебраический способы отбора корней.	1
23.	Тригонометрические уравнения, содержащие знак абсолютной величины.	1
24-25	Занятия-практикумы по закреплению теоретического материала темы.	2
Тема №5 « Решение уравнений с использованием свойств, входящих в них функций (6 часов)
26.	Использование ОДЗ	1
27.	Использование ограничений функций.	1
28.	Использование монотонности функций. Использование графиков функций.	1
29.	Использование свойств синуса и косинуса.	1
30-31	Занятия-практикумы по закреплению теоретического материала темы.	2
Итоговое повторение (4 часа)
32-33	Занятия-практикумы по закреплению изученного материала.	3
34	Зачёт	1
11 класс (34 часа)
Тема №1 « Решение уравнений с параметрами» ( 5 часов)
1.	Решение линейных уравнений с параметрами.	1
2.	Решение квадратных уравнений с параметрами.	1
3.	Существование корней трёхчлена второй степени с параметрами, выявление их количества. Расположение корней на числовой прямой относительно заданных точек, промежутков.	1
4-5.	Уроки-практикумы по закреплению теоретического материала темы	2
Тема №2 « Решение уравнений  и неравенств, содержащих радикалы (5часов)
6.	Возведение в степень. Уравнения вида .	1
7.	Умножение уравнения на функцию.	1
8.	Уравнение вида .	1
9.	Уравнение вида	1
10	Урок-практикум.	1
Тема №3 « Решение некоторых уравнений и неравенств, сведением их к решению систем уравнений или неравенств относительно той же неизвестной ( 6 часов)
11-12	Уравнения вида	2
13-14	Неравенства вида	2
15.	Использование ограниченности функции.	1
16.	Урок-практикум.	1
Тема №4 « Применение производной» (5 часа)
17.	Использование монотонности функции.	1
18.	Использование наибольшего и наименьшего значений функции.	1
19.	Применение теоремы Лагранжа.	1
20-21	Уроки-практикумы.	2
Тема №5 « Уравнения и неравенства, содержащие логарифмы           (8 часов)
22.	Переход к числовому  основанию. Переход к основанию, содержащему неизвестную.	1
23.	Уравнения вида	1
24	Уравнения вида	1
25	Неравенства вида	1
26.	Уравнения и неравенства, содержащие неизвестную в основании и показателе степени.	1
27-29	Занятия- практикумы по закреплению теоретического материала темы.	3
Итоговое повторение (5 часов)
30-32	Решение задач по изученному курсу.	3
33-34	Итоговый зачёт.	2

 

ЗАЧЁТ №1 (9 класс)

 

Вариант 1

1.     Разложите выражение на множители:

                                               2а² - х² - ах – а + х.      

2. Решите уравнение:

(х – 2)(х – 1)(х + 2)(х + 3) = 60.

 

3. Решить неравенство:

(х² + 1)² – 12(х² +1) + 20   0.

4. Решите систему уравнений:

 

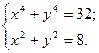
Вариант 2

1.     Разложите выражение на множители:

(х + 3)(х – 2)(х + 1)х + 8;

2. Решите уравнение:

(х² - 5х + 7)² - (х – 3)(х – 2) = 1.

3. Решить неравенство:

(х² + 2х)² + 3(х + 1)² > 3

4. Решите систему уравнений:

 

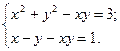
Вариант 3

1.     Разложите выражение на множители:

(х + 3)(х – 2)(х + 1)х + 8;

2.  Решите уравнение:

х – 2х – 6х + 12х² + х – 2 = 0

3. Решить неравенство:

(х² – 4х – 15)(х² - 4х + 10)  -150

 

4. Решите систему уравнений:

 

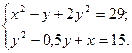
ЗАЧЁТ №2 (10 класс)

 

Вариант 1

1. Решите уравнение

|х| - 2|х + 1| + 3| 2х - 4| = 1.

2. Решите уравнение

 

3. Решить уравнение      cos³х + sin³х = cos2х. В ответе записать количество корней уравнения, принадлежащих отрезку

 

Вариант 2

1. Решите неравенство:

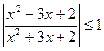
2. Решите уравнение:

3. Решить уравнение      cos³х + sin³х = cos2х. В ответе записать количество корней уравнения, принадлежащих отрезку

Вариант 3

1. Решите уравнение:

(х – 4) + (х + 3) = 626.

2.  Решите неравенство

|х² + 5х + 6| > 3

      3.    Решите уравнение  (sin 4х + cos4х)² = 16 sin2х·cos³2х - 8sin2х·cos2х.

В ответе записать количество корней уравнения, принадлежащих интервалу.

ЗАЧЁТ №3 (11 класс)

 

Вариант 1

1.                 При каком значении параметра а уравнение |х² - 4х - 5| = а имеет ровно три решения.

2.                 Решите уравнение

.

3.                 Решите уравнение log(log(х² – 2х)) =0.

4.                 Решить уравнение 2=9. В ответе записать корень   уравнения (в градусах), принадлежащий отрезку , а если таких корней несколько, то – их сумму.

5.                      Найти число положительных корней уравнения

.

 

Вариант 2.

1.                 Найдите все значения а, при каждом из которых уравнение                   (а + 1)х² – ах + (а – 3) = 0 имеет не более одного действительного корня.

2.                 Решите уравнение

3.                 Решите уравнение

 (log (cosx))² = 1

4.                 Решить уравнение

5.                      Найти число корней уравнения

(cos8x + cos2x - ctgx·sin2x)= 0.

 

Вариант 3.

1.                 Решите уравнение х² + |х| + а = 0

2.                 Решите уравнение

3.                 Найти наибольшее целое значение функции                                                у =27log(х - 4) – х |х - 13| + 19.

4.                 Решите неравенство

5.                       Найдите число корней уравнения

sin2πx · ctg = 0,

           принадлежащих отрезку

 

Литература:

1.           С.Н. Олехник, М.К. Потапов, П.И. Пасиченко «Уравнения и неравенства».

      Дрофа – 2001 г.

2.           Единый государственный экзамен. Математика. КИМ.  Раздел С.

      «Просвещение» 2009 – 2011г.

3.   М.И. Сканави. «Сборник задач по математике» Алгебра. ОНИКС 21 ВЕК –            

       Мир и Образование. 2010 г.

4.   П.И. Горнштейн, В.Б. Полонский, М.С. Якир «Задачи с параметрами».

       «Илекса. Гимназия» , Москва – Харьков. 2010 г.

5.        Е.Е. Мордовина « Исследование корней трёхчлена второй степени с

параметром». Тамбов. ОИПКРО. 2002 г.

6.        Н.Б. Яновская, Г.Б. Яновский «К вопросу решения тригонометрических

уравнений». Журнал «Математика в школе» №3 – 2005 г.

7.        Ю.П. Золотухин «Уравнения аsinх +  bcosх + с = 0 и его применение».

       Журнал «Математика в школе» №6 – 2005 г.

8.        И.И. Чучаева, Т.В. Денисова «Выпуклые функции и уравнения».

Журнал «Математика в школе» № 5 – 2005 г.

9.        Ю.Н. Гинев «Математика» Задачник, часть 1 и 2. Учебное пособие для

подготовки к рейтинговому тестированию при МИСиС. Москва – 2005 г.

10.   И.М. Петрушенко, В.И. Прохоренко, В.Ф. Сафонов «Сборник задач по

алгебре, геометрии и началам анализа» Москва. Издательство МЭИ. 2007г.