Рабочая программа по геометрии за 7 класс 2 часа в неделю

 

Рассмотрено на заседании ШМО Руководитель ШМО ________/Александрова Н.А. _/ ФИО Протокол № 1 от «  28  »   августа   2020_г.

«Согласовано» Зам. дир. по НМР МБОУ «СОШ №6 им.Н.З.Ульяненко» г.Воткинска ___________/__Гордиенко М.А._/ ФИО «28»_августа_2020___г.

«Утверждаю» Директор МОУ «СОШ №6 им.Н.З.Ульяненко»  г.Воткинска _____________/Афонина М.Ю._/ ФИО Приказ № ________ от «28»_   августа_2020г.

 

Принято на заседании

педагогического совета

протокол № __    1__

от «28»  августа  2020_ г.

 

РАБОЧАЯ ПРОГРАММА ПЕДАГОГА

Тарасовой Татьяны Ивановны, высшая квалификационная категория

МБОУ «СОШ № 6 имени Героя Советского Союза Н.З.Ульяненко»

составлена в соответствии с требованиями федерального

 государственного образовательного стандарта ООО

 

Предмет:                                                                    геометрия

Класс:                                                                         7б

Количество часов в неделю:                                    2 часа

Количество часов в учебном году:                         68  часов

 

 

 

 

 

2020- 2021 учебный год

                                                                                         

 

Пояснительная записка

 Рабочая программа по геометрии для 7 класса основной общеобразовательной школы составлена на основе Федерального государственного образовательного стандарта основного общего образования, Фундаментального ядра содержания общего образования; Требований к результатам освоения основной общеобразовательной программы основного общего образования; Примерной программы основного общего образования по геометрии (Сборник нормативных документов Математика. М.: Дрофа, 2010), Сборник рабочих программ геометрия 7-9 классы, составитель Бурмистрова Т.А., М.: Просвещение, 2014

       

Нормативное обеспечение программы:

1.    Закон РФ 273-ФЗ от 29.12.2012г. «Об образовании в РФ».

2.    Федераль­ный государственный образовательный стандарт основного общего образования, утвержденный Приказом Министерства образования и науки Российской Федерации от «17»  декабря  2010 г. № 1897  (в действующей редакции от 31.12.2015)

3.    Программы общеобразовательных учреждений. Геометрия. 7-9 классы. Составитель Бурмистрова Т. А. – М.: Просвещение, 2013.

4.      Учебного плана школы;

5.      Положения о рабочей программе учителя  МБОУ «СОШ № 6 имени Героя Советского Союза Н.З. Ульяненко» города Воткинска Удмуртской Республики по ФГОС

          

Цель и задачи курса

  Цель:

 

·         овладение системой математических знаний и умений, необходимых для            применения в практической деятельности, изучения смежных дисциплин,   продолжения образования;

·         интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

·         формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

·         воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

 

 Задачи:

·         введение терминологии и отработка умения ее грамотно использования;

·         развитие навыков изображения планиметрических фигур и простейших геометрических конфигураций;

·         совершенствование навыков применения свойств геометрических фигур как опоры при решении задач;

·         формирования умения решения задач на вычисление геометрических величин с применением изученных свойств фигур и формул;

·         совершенствование навыков решения задач на доказательство;

·         отработка навыков решения задач на построение с помощью циркуля и линейки;

расширение знаний учащихся о треугольниках, четырёхугольниках и окружности

 

 

 

 

 

                          Общая характеристика курса геометрии 7-9 классов

Рабочая программа основного общего образования по геометрии составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте основного общего образования по предмету. В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.

 Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Геометрия – один из важнейших компонентов математического образования. Она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции, математической культуры, эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

        Овладение учащимися системой геометрических знаний и умений необходимо в повседневной жизни для изучения смежных дисциплин и продолжения образования.

        Практическая значимость школьного курса геометрии обусловлена тем, что её объектом являются пространственные формы и количественные отношения действительного мира. Геометрическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.

        Геометрия является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно-научного цикла, в частности к физике. Развитие логического мышления учащихся при обучении геометрии способствует также усвоению предметов гуманитарного цикла. Практические умения и навыки геометрического характера необходимы для трудовой деятельности и профессиональной подготовки школьников.

        Развитие у учащихся правильных представлений о сущности и происхождении геометрических абстракций, соотношении реального и идеального, характере отражения математической наукой явлений и процессов реального мира, месте геометрии в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся, а также формированию качеств мышления, необходимых для адаптации в  современном информационном обществе.

        Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, геометрия развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.

        Геометрия существенно расширяет кругозор учащихся, знакомя их с индукцией и дедукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагированием, аналогией. Активное использование задач на всех этапах учебного процесса развивает творческие способности школьников.

        При обучении геометрии формируются умения и навыки умственного труда – планирование своей работы, поиск рациональных путей её выполнения, критическая оценка результатов. В процессе обучения геометрии школьники должны научиться излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобрести навыки четкого, аккуратного и грамотного выполнения математических записей.

 

 Место предмета в учебном плане школы

 

Согласно учебному плану на изучение математики в 7-9 классах на ступени основного общего образования отводится 5 ч в неделю, в том числе на изучение геометрии 2 часа в неделю:

7 класс – 68 часов (34 уч. недель);

8 класс – 68 часов (34 уч. недель);

9 класс – 68 часов (34 уч. недели)

Таким образом, курс геометрии рассчитан на 204 часа.

 

Используемый учебно-методический комплект:

 

1.    Атанасян Л. С. Геометрия. 7-9 кл.: учебник / Л.С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2017- 2018.

2.    Атанасян Л. С. Изучение геометрии в 7-9 классах: методические рекомендации: книга для учителя / Л. С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др.]- М.: Просвещение, 2014.

3.    Лысенко Ф. Ф. Геометрия. 7 класс. Рабочая тетрадь для тренировки и мониторинга / Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. –Ростов-на-Дону.: Легион, 2017.

4.    Мельникова Н. Б. Контрольные работы по геометрии, 7 класс: к учебнику Л. С. Атанасяна « Геометрия, 7-9»/ Н. Б. Мельникова-М.: Изд. «Экзамен», 2017.

5.    Алтынов П. И. Геометрия. Тесты. 7-9 классы: учеб.-мет. пособие / П. И. Алтынов-М.: Дрофа, 2017.

 

Формы организации образовательного процесса:

 

К наиболее приемлемым формам организации учебных занятий по математике можно отнести:

- традиционные уроки;

- уроки контроля знаний, умений и навыков;

-  самостоятельная работа учащихся;

- творческая деятельность;

- исследовательские проекты;

- публичные презентации;

- лекции;

- практическая деятельность (решение задач, выполнение практических работ).

 

 

 

 

 

Планируемые результаты изучения учебного предмета  «Геометрия» в 7-9 классах

 

Планируемые результаты по геометрии 7 класса:

ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

Выпускник научится:

• Оперировать на базовом уровне понятиями геометрических фигур;
• извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде;
• применять для решения задач геометрические факты, если условия их применения заданы в явной форме;
• решать задачи на нахождение геометрических величин по образцам или алгоритмам.

В повседневной жизни и при изучении других предметов:

• использовать свойства геометрических фигур для решения типовых задач, возникающих в ситуациях повседневной жизни, задач практического содержания.

Выпускник получит возможность научиться:

• Оперировать понятиями геометрических фигур;

• извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;
• применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения;
• формулировать в простейших случаях свойства и признаки фигур;

В повседневной жизни и при изучении других предметов:

• использовать свойства геометрических фигур для решения задач практического характера и задач из смежных дисциплин.

ОТНОШЕНИЯ

выпускник научится:

• Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция.

В повседневной жизни и при изучении других предметов:

• использовать отношения для решения простейших задач, возникающих в реальной жизни.

выпускник получит возможность научиться:

• Оперировать понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция, подобие фигур, подобные фигуры, подобные треугольники;
• применять теорему Фалеса и теорему о пропорциональных отрезках при решении задач;
• характеризовать взаимное расположение прямой и окружности, двух окружностей.

В повседневной жизни и при изучении других предметов:

• использовать отношения для решения задач, возникающих в реальной жизни.

ИЗМЕРЕНИЯ И ВЫЧИСЛЕНИЯ

Выпускник научится:

• Выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;
• применять формулы периметра при вычислениях, когда все данные имеются в условии;

В повседневной жизни и при изучении других предметов:

• вычислять расстояния на местности в стандартных ситуациях.

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

Выпускник научится:

• Изображать типовые плоские фигуры и фигуры в пространстве от руки и с помощью инструментов.

     В повседневной жизни и при изучении других предметов:

• выполнять простейшие построения на местности, необходимые в реальной жизни.

Выпускник получит возможность научиться:

• Изображать геометрические фигуры по текстовому и символьному описанию;
• свободно оперировать чертежными инструментами в несложных случаях,
• выполнять построения треугольников, применять отдельные методы построений циркулем и линейкой и проводить простейшие исследования числа решений;
• изображать типовые плоские фигуры и объемные тела с помощью простейших компьютерных инструментов.

В повседневной жизни и при изучении других предметов:

• выполнять простейшие построения на местности, необходимые в реальной жизни;
• оценивать размеры реальных объектов окружающего мира.

ИСТОРИЯ МАТЕМАТИКИ

выпускник научится:

• Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;
• знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;
• понимать роль математики в развитии России.

выпускник получит возможность научиться:

• Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;
• понимать роль математики в развитии России.

 

Планируемые результаты по геометрии 8 класса:

ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

Выпускник научится:

• извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде;
• применять для решения задач геометрические факты, если условия их применения заданы в явной форме;
• решать задачи на нахождение геометрических величин по образцам или алгоритмам.

В повседневной жизни и при изучении других предметов:

• использовать свойства геометрических фигур для решения типовых задач, возникающих в ситуациях повседневной жизни, задач практического содержания.

получит возможность научиться:

• извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;
• применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения;
• формулировать в простейших случаях свойства и признаки фигур;
• доказывать геометрические утверждения;
• владеть стандартной классификацией плоских фигур (треугольников и четырехугольников).

В повседневной жизни и при изучении других предметов:

• использовать свойства геометрических фигур для решения задач практического характера и задач из смежных дисциплин.

ОТНОШЕНИЯ

Выпускник получит возможность научиться:

• Оперировать понятиями: перпендикуляр, наклонная, проекция, подобие фигур, подобные фигуры, подобные треугольники;
• применять теорему Фалеса и теорему о пропорциональных отрезках при решении задач;
• характеризовать взаимное расположение прямой и окружности, двух окружностей.

В повседневной жизни и при изучении других предметов:

• использовать отношения для решения задач, возникающих в реальной жизни.

ИЗМЕРЕНИЯ И ВЫЧИСЛЕНИЯ

Выпускник научится:

• применять формулы площади и объема, площади поверхности отдельных многогранников при вычислениях, когда все данные имеются в условии;
• применять теорему Пифагора для вычисления длин, расстояний, площадей в простейших случаях.

В повседневной жизни и при изучении других предметов:

• вычислять расстояния на местности в стандартных ситуациях, площади в простейших случаях, применять формулы в простейших ситуациях в повседневной жизни.

Выпускник получит возможность научиться:

• Оперировать представлениями о площади, объеме как величинами. Применять теорему Пифагора, формулы площади, объема при решении многошаговых задач, в которых не все данные представлены явно, а требуют вычислений, оперировать более широким количеством формул длины, площади, объема, вычислять характеристики комбинаций фигур (окружностей и многоугольников) вычислять расстояния между фигурами, проводить вычисления на основе равновеликости и равносоставленности;
• проводить простые вычисления на объемных телах;
• формулировать задачи на вычисление длин, площадей и объемов и решать их.

В повседневной жизни и при изучении других предметов:

• проводить вычисления на местности;
• применять формулы при вычислениях в смежных учебных предметах, в окружающей действительности.

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

Выпускник научится:

• Изображать типовые плоские фигуры и фигуры в пространстве от руки и с помощью инструментов.

В повседневной жизни и при изучении других предметов:

• выполнять простейшие построения на местности, необходимые в реальной жизни.

Выпускник получит возможность научиться:

• Изображать геометрические фигуры по текстовому и символьному описанию;
• свободно оперировать чертежными инструментами в несложных случаях,
• изображать типовые плоские фигуры и объемные тела с помощью простейших компьютерных инструментов.

В повседневной жизни и при изучении других предметов:

• выполнять простейшие построения на местности, необходимые в реальной жизни;
• оценивать размеры реальных объектов окружающего мира.

ИСТОРИЯ МАТЕМАТИКИ

выпускник научится :

• Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;
• знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;
• понимать роль математики в развитии России.

выпускник получит возможность научиться:

• Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;
• понимать роль математики в развитии России.

 

Планируемые результаты по геометрии в 9 классе

 

ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

Выпускник научится:

• Оперировать на базовом уровне понятиями геометрических фигур;
• извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде;
• применять для решения задач геометрические факты, если условия их применения заданы в явной форме;
• решать задачи на нахождение геометрических величин по образцам или алгоритмам.

В повседневной жизни и при изучении других предметов:

• использовать свойства геометрических фигур для решения типовых задач, возникающих в ситуациях повседневной жизни, задач практического содержания.

выпускник получит возможность научиться в 7-9 классах:

• Оперировать понятиями геометрических фигур;

• извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;
• применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения;
• формулировать в простейших случаях свойства и признаки фигур;
• доказывать геометрические утверждения;
• владеть стандартной классификацией плоских фигур (треугольников и четырехугольников).

В повседневной жизни и при изучении других предметов:

• использовать свойства геометрических фигур для решения задач практического характера и задач из смежных дисциплин.

ОТНОШЕНИЯ

выпускник научится:

• Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция.

В повседневной жизни и при изучении других предметов:

• использовать отношения для решения простейших задач, возникающих в реальной жизни.

выпускник получит возможность:

• Оперировать понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция, подобие фигур, подобные фигуры, подобные треугольники;
• применять теорему Фалеса и теорему о пропорциональных отрезках при решении задач;
• характеризовать взаимное расположение прямой и окружности, двух окружностей.

В повседневной жизни и при изучении других предметов:

• использовать отношения для решения задач, возникающих в реальной жизни.

ИЗМЕРЕНИЯ И ВЫЧИСЛЕНИЯ

выпускник научится:

• Выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;
• применять формулы периметра, площади и объема, площади поверхности отдельных многогранников при вычислениях, когда все данные имеются в условии;
• применять теорему Пифагора, базовые тригонометрические соотношения для вычисления длин, расстояний, площадей в простейших случаях.

В повседневной жизни и при изучении других предметов:

• вычислять расстояния на местности в стандартных ситуациях, площади в простейших случаях, применять формулы в простейших ситуациях в повседневной жизни.

выпускник получит возможность научиться:

• Оперировать представлениями о длине, площади, объеме как величинами. Применять теорему Пифагора, формулы площади, объема при решении многошаговых задач, в которых не все данные представлены явно, а требуют вычислений, оперировать более широким количеством формул длины, площади, объема, вычислять характеристики комбинаций фигур (окружностей и многоугольников) вычислять расстояния между фигурами, применять тригонометрические формулы для вычислений в более сложных случаях, проводить вычисления на основе равновеликости и равносоставленности;
• проводить простые вычисления на объемных телах;
• формулировать задачи на вычисление длин, площадей и объемов и решать их.

В повседневной жизни и при изучении других предметов:

• проводить вычисления на местности;
• применять формулы при вычислениях в смежных учебных предметах, в окружающей действительности.

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

выпускник научится:

• Изображать типовые плоские фигуры и фигуры в пространстве от руки и с помощью инструментов.

В повседневной жизни и при изучении других предметов:

• выполнять простейшие построения на местности, необходимые в реальной жизни.

выпускник получит возможность научиться:

• Изображать геометрические фигуры по текстовому и символьному описанию;
• свободно оперировать чертежными инструментами в несложных случаях,
• выполнять построения треугольников, применять отдельные методы построений циркулем и линейкой и проводить простейшие исследования числа решений;
• изображать типовые плоские фигуры и объемные тела с помощью простейших компьютерных инструментов.

В повседневной жизни и при изучении других предметов:

• выполнять простейшие построения на местности, необходимые в реальной жизни;
• оценивать размеры реальных объектов окружающего мира.

ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

выпускник научится:

• Строить фигуру, симметричную данной фигуре относительно оси и точки.

В повседневной жизни и при изучении других предметов:

• распознавать движение объектов в окружающем мире;
• распознавать симметричные фигуры в окружающем мире.

выпускник получит возможность научиться:

• Оперировать понятием движения и преобразования подобия, владеть приемами построения фигур с использованием движений и преобразований подобия, применять полученные знания и опыт построений в смежных предметах и в реальных ситуациях окружающего мира;
• строить фигуру, подобную данной, пользоваться свойствами подобия для обоснования свойств фигур;
• применять свойства движений для проведения простейших обоснований свойств фигур.

В повседневной жизни и при изучении других предметов:

• применять свойства движений и применять подобие для построений и вычислений.

ВЕКТОРЫ И КООРДИНАТЫ НА ПЛОСКОСТИ

выпускник научится:

• Оперировать на базовом уровне понятиями вектор, сумма векторов, произведение вектора на число, координаты на плоскости;
• определять приближенно координаты точки по ее изображению на координатной плоскости.

В повседневной жизни и при изучении других предметов:

• использовать векторы для решения простейших задач на определение скорости относительного движения.

выпускник получит возможность научиться:

• Оперировать понятиями вектор, сумма, разность векторов, произведение вектора на число, угол между векторами, скалярное произведение векторов, координаты на плоскости, координаты вектора;
• выполнять действия над векторами (сложение, вычитание, умножение на число), вычислять скалярное произведение, определять в простейших случаях угол между векторами, выполнять разложение вектора на составляющие, применять полученные знания в физике, пользоваться формулой вычисления расстояния между точками по известным координатам, использовать уравнения фигур для решения задач;
• применять векторы и координаты для решения геометрических задач на вычисление длин, углов.

В повседневной жизни и при изучении других предметов:

• использовать понятия векторов и координат для решения задач по физике, географии и другим учебным предметам.

ИСТОРИЯ МАТЕМАТИКИ

выпускник научится:

• Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;
• знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;
• понимать роль математики в развитии России.

выпускник получит возможность научиться:

• Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;
• понимать роль математики в развитии России.

МЕТОДЫ МАТЕМАТИКИ

выпускник научится:

• Выбирать подходящий изученный метод для решения изученных типов математических задач;
• Приводить примеры математических закономерностей в окружающей действительности и произведениях искусства.

выпускник получит возможность научиться:

• Используя изученные методы, проводить доказательство, выполнять опровержение;
• выбирать изученные методы и их комбинации для решения математических задач;
• использовать математические знания для описания закономерностей в окружающей действительности и произведениях искусства;
• применять простейшие программные средства и электронно-коммуникационные системы при решении математических задач.

 

 

Содержание тем учебного курса

 

Содержание курса геометрии 7 класс

 

 Начальные геометрические сведения 10ч

Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые

 Треугольник 18 ч.

Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Основные задачи на построение с помощью циркуля и линейки.

Параллельные прямые 11 ч.

 Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых.

 Соотношения между сторонами и углами треугольника 21ч.

 Сумма углов треугольника. Соотношения между сторонами и углами треугольника. Неравенство треугольника. Некоторые свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Задачи на построение.

 Повторение 8 ч.

Повторить и обобщить изученный материал.

 

 

 

 

Содержание курса геометрии 8 класс

Повторение курса геометрии 7 класса (2 часа)

Четырехугольники (14 часов)

Многоугольник, выпуклый многоугольник, четырехуголь­ник. Параллелограмм, его свойства и признаки. Трапеция. Пря­моугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.

Площадь (14 часов)

Понятие площади многоугольника. Площади прямоуголь­ника, параллелограмма, треугольника, трапеции. Теорема Пи­фагора.

Подобные треугольники (19часов)

Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треуголь­ника.

Окружность (17 часов)

Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.

Повторение. Решение задач. (2 часа)

Содержание курса геометрии 9 класс

Векторы и метод координат (18 ч.)

Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов (11 ч.)

Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических задачах.

Длина окружности и площадь круга (12 ч.)

Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.

Движения (8 ч.)

Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения.

Начальные сведения из стереометрии (8 ч.)

Предмет стереометрия. Многогранник. Призма. Параллелепипед. Цилиндр. Конус. Сфера и шар. Об аксиомах планиметрии. Некоторые сведения о развитии геометрии

Повторение (9+2 ч.)

Параллельные прямые. Треугольники. Четырехугольники. Окружность.

Тематический план

 

№	Содержание учебного материала	Количество часов	Контрольные работы
1	Начальные геометрические сведения	10	Контрольная работа №1 по теме «Основные свойства простейших геометрических фигур. Смежные и вертикальные углы»
2	Треугольники	18	Контрольная работа №2 по теме «Треугольники»
3	Параллельные прямые	11	Контрольная работа №3 по теме «Параллельные прямые»
4	Соотношение между сторонами и углами треугольника	21	Контрольная работа №4 по теме «Сумма углов треугольника. Соотношение между сторонами и углами треугольника» . Контрольная работа №5 по теме «Прямоугольный треугольник. Построение треугольника по трем элементам»
5	Повторение	8	Итоговая контрольная работа №6. Административная контрольная работа
	итого	68	7

 

Тематическое планирование

 

№ урока	Тема урока		Основные виды учебной деятельности обучающихся
Начальные геометрические сведения 10ч.
1	Прямая и отрезок	Иметь представление о прямой  и отрезке Объясняют что такое отрезок
2	Луч и угол	Иметь представление о геометрических  фигурах луч и угол Объясняют что такое луч и угол
3	Сравнение отрезков и углов	Уметь сравнивать отрезки и углы Объясняют, какие фигуры называются равными, как сравнивают отрезки и углы, что такое середина отрезка и биссектриса угла
4	Измерение отрезков	С помощью инструментов уметь измерять отрезки Объясняют, как измеряют отрезки, что называется масштабным отрезком
5	Решение задач по теме «Измерение отрезков»	С помощью инструментов уметь измерять углы Объясняют, как измеряют углы, что такое градус и градусная мера угла
6	Измерение углов	Уметь находить градусную меру угла Объясняют, какой угол называется прямым, тупым, острым, развернутым
7	Смежные и вертикальные углы	Распознавать на чертежах и изображать вертикальные и смежные углы. Находить градусную меру вертикальных и смежных углов, используя их свойства Объясняют, какие углы называются смежными и какие вертикальными. Формулируют и обосновывают утверждения о свойствах смежных и вертикальных углов
8	Перпендикулярные прямые	Распознавать на чертежах и изображать перпендикулярные прямые. Объясняют, какие прямые называются перпендикулярными. Формулируют и обосновывают утверждение о свойстве двух перпендикуляр-ных прямых к третьей
9	Решение задач	Обобщить и систематизировать знания о свойствах измерения длин отрезков, градусной меры угла Изображают и распознают указанные простейшие фигуры на чертежах. Решают задачи, связанные с этими простейшими фигурами
10	Контрольная работа №1 по теме «Начальные геометрические сведения	Продемонстрировать уровень владения изученным материалом Распознают геометрические фигуры и их отношения. Решают задачи на вычисление длин отрезков градусных мер углов с необходимыми теоретическими обоснованиями
Треугольники 18 ч.
11	Треугольник	Иметь представление о геометрической фигуре «треугольник», ее элементах Объясняют, какая фигура называется треугольником, что такое вершины, стороны, углы и периметр треугольника
12	Первый признак равенства треугольников	Уметь распознавать и изображать на чертежах и рисунках треугольники Объясняют, какие треугольники называются равными. Изображают и распознают на чертежах треугольники и их элементы
13	Решение задач на применение первого признака равенства треугольников	Сформулировать и доказать первый признак равенства треугольников Объясняют что такое теорема и доказательство. Формулируют и доказывают первый признак равенства треугольников
14	Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника	Иметь представление о перпендикуляре к прямой. Сформулировать и доказать теорему о перпендикуляре к прямой Объясняют, какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой. Формулируют и доказывают теорему о перпендикуляре к прямой
15	Свойства равнобедренного треугольника	Иметь представление о медиане, биссектрисе и высоте треугольника, их свойствах Объясняют, какие отрезки называются медианой, биссектрисой и высотой треугольника. Формулируют их свойства
16	Свойства равнобедренного треугольника	Иметь представление о равнобедренном треугольнике, уметь доказывать теоремы о свойствах равнобедренного треугольника Объясняют, какой треугольник называется равнобедренным и какой равносторонним. Формулируют и доказывают теоремы о свойствах равнобедренного треугольника
17	Второй признак равенства треугольников	Сформулировать и доказать первый признак равенства треугольников Формулируют и доказывают второй и третий признак равенства треугольников
18	Второй признак равенства треугольников	Научиться решать задачи связанные с признаками и свойствами треугольников Решают задачи, связанные с признаками равенства треугольников и свойствами равнобедренного треугольника
19	Третий признак равенства треугольников	Научиться решать задачи связанные с признаками и свойствами треугольников Решают задачи, связанные с признаками равенства треугольников и свойствами равнобедренного треугольника
20	Решение задач	Научиться решать задачи связанные с признаками и свойствами треугольников Решают задачи, связанные с признаками равенства треугольников и свойствами равнобедренного треугольника
21	Задачи на построение. Окружность	В результате практических действий и наблюдений закрепить знания по теме Объясняют что такое определение. Формулируют определение окружности. Объясняют что такое центр, радиус, хорда и диаметр окружности
22	Задачи на построение. Деление отрезка пополам. Построение угла равного данному	Научиться решать несложные задачи на построение с помощью циркуля и линейки Объясняют, как отложить на данном луче от его начала отрезок, равный данному
23	Задачи на построение. Построение биссектрисы угла	Научиться решать несложные задачи на построение с помощью циркуля и линейки Объясняют построение угла, равного данному, биссектрисы данного угла
24	Решение задач по теме «Треугольники»	Научиться решать несложные задачи на построение с помощью циркуля и линейки Объясняют построение перпендикулярных прямых, середины данного отрезка
25	Решение задач на построение	Обобщить и систематизировать знания об отношениях фигур и их элементов Анализируют и осмысливают текст задачи, моделируют условие с помощью схем, чертежей, реальных предметов.
26	Решение задач. Подготовка к контрольной работе	Обобщить и систематизировать знания об отношениях фигур и их элементов Анализируют и осмысливают текст задачи, моделируют условие с помощью схем, чертежей, реальных предметов.
27	Контрольная работа №2 по теме «Треугольники»	Продемонстрировать уровень владения изученным материалом Распознают на чертежах геометрические фигуры и их элементы.  Решают задачи на доказательство и вычисление
28	Работа над ошибками	Анализ ошибок
Параллельные прямые 11ч.
29	Определение параллельных прямых. Признаки параллельности двух прямых	В результате практических действий и наблюдений закрепить знания по теме Формулируют определение параллельных прямых. Объясняют что такое секущая. С помощью рисунка, называют пары углов, образованных при пересечении двух прямых секущей
30	Признаки параллельности двух прямых	Сформулировать и доказать теоремы, выражающие признаки параллельности двух прямых Формулируют и доказывают теоремы, выражающие признаки параллельности двух прямых
31	Решение задач на применение признаков параллельности прямых	Научиться решать задачи связанные с признаками параллельности двух прямых Решают задачи на доказательство связанные с признаками параллельности двух прямых.
32	Об аксиомах геометрии. Аксиома параллельности прямых	В результате практических действий и наблюдений закрепить знания по теме Рассказывают о практических способах построения параллельных прямых.
33	Свойства параллельных прямых	Уметь объяснять, что такое аксиома. Сформулировать аксиому параллельных прямых и следствия из нее Объясняют, что такое аксиомы геометрии, приводят примеры аксиом. Формулируют аксиому параллельных прямых  и выводят следствия из нее
34	Свойства параллельных прямых. Решение задач	Сформулировать и доказать теоремы о свойствах параллельных прямых, обратные теоремам о признаках параллельности двух прямых. Уметь объяснять, что такое условие и заключение теоремы, какая теорема называется обратной по отношению к данной теореме Формулируют и доказывают теоремы о свойствах параллельных прямых, обратные теоремам о признаках параллельности двух прямых. Объясняют, что такое условие и заключение теоремы, какая теорема называется обратной по отношению к данной теореме
35	Решение задач по теме «Параллельность прямых»	Научиться решать задачи связанные с признаками параллельности двух прямых Анализируют и осмысливают текст задачи, моделируют условие с помощью схем, чертежей, реальных предметов.
36	Решение задач на свойства параллельных прямых	Уметь объяснять, в чем заключается метод доказательства от противного; сформулировать и доказать теоремы об углах с соответственно параллельными и перпендикулярными сторонами Объясняют, в чем заключается метод доказательства от противного; формулируют и доказывают теоремы об углах с соответственно параллельными и перпендикулярными сторонами
37	Решение задач. Обобщение	Научиться решать задачи на вычисление, доказательство и построение связанные с признаками параллельности двух прямых Решают задачи на вычисление, доказательство и построение, связанные с параллельными прямыми
38	Решение задач. Подготовка к контрольной работе	Научиться решать задачи связанные с признаками параллельности двух прямых Анализируют и осмысливают текст задачи, моделируют условие с помощью схем, чертежей, реальных предметов.
39	Контрольная работа №3 по теме «Параллельные прямые»	Продемонстрировать уровень владения изученным материалом Распознают на чертежах геометрические фигуры и их элементы.  Решают задачи на доказательство и вычисление
Соотношения между сторонами и углами треугольника 21ч.
40	Сумма углов треугольника	Сформулировать и доказать теорему о сумме углов треугольника и ее следствие о внешнем угле треугольника Формулируют и доказывают теорему о сумме углов треугольника и ее следствие о внешнем угле треугольника
41	Внешний угол треугольника. Теорема о внешнем угле треугольника	Уметь различать на чертежах остроугольный, тупоугольный и прямоугольный треугольники Проводят классификацию треугольников по углам
42	Теорема о соотношениях между сторонами и углами треугольника	Сформулировать и доказать теорему о соотношениях между сторонами и углами треугольника Формулируют  и доказывают теорему о соотношениях между сторонами и углами треугольника (прямое и обратное утверждение)
43	Теорема о соотношениях между сторонами и углами треугольника. Решение задач.	Сформулировать и доказать следствия из теоремы о соотношениях между сторонами и углами треугольника Формулируют и доказывают следствия из теоремы о соотношениях между сторонами и углами треугольника
44	Неравенство треугольника	Сформулировать и доказать теорему о неравенстве треугольника Формулируют и доказывают теорему о неравенстве треугольника
45	Решение задач. Подготовка к контрольной работе	Продемонстрировать уровень владения изученным материалом Распознают на чертежах геометрические фигуры и их элементы.  Решают задачи на доказательство и вычисление
46	Контрольная работа №4 по теме «Соотношения между сторонами и углами треугольника»	Продемонстрировать уровень владения изученным материалом Распознают на чертежах геометрические фигуры и их элементы.  Решают задачи на доказательство и вычисление
47	Анализ ошибок контрольной работы	Сформулировать и доказать свойства катета прямоугольного треугольника, лежащего против угла Формулируют и доказывают свойство катета прямоугольного треугольника, лежащего против угла в  (прямое и обратное утверждение)
48	Некоторые свойства прямоугольных треугольников	Сформулировать и доказать признак равенства прямоугольных треугольников по гипотенузе и острому углу Формулируют и доказывают признак равенства прямоугольных треугольников по гипотенузе и острому углу
49	Некоторые свойства прямоугольных треугольников. Решение задач	Сформулировать и доказать признак равенства прямоугольных треугольников по гипотенузе и катету Формулируют и доказывают признак равенства прямоугольных треугольников по гипотенузе и катету
50	Признаки равенства прямоугольных треугольников	Научиться решать несложные задачи на построение треугольника по трем элементам с помощью циркуля и линейки Объясняют, какой отрезок называется наклонной, проведенной из данной точки к данной прямой Доказывают, что перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из этой же точки к этой прямой. Формулируют определение расстояния от точки до прямой
51	Решение задач по теме «Прямоугольный треугольник»	Научиться решать несложные задачи на построение треугольника по трем элементам с помощью циркуля и линейки Решают задачи на вычисление, доказательство и построение, связанные с расстоянием от точки до прямой
52	Решение задач по теме «Прямоугольный треугольник»	Сформулировать и доказать свойство о равноудалённости точек параллельных прямых. Сформулировать определение между двумя параллельными прямыми
53	Расстояние от точки до прямой. Расстояние между параллельными прямыми	Научиться решать несложные задачи на построение треугольника по трем элементам с помощью циркуля и линейки Решают задачи на вычисление, доказательство и построение, связанные с расстоянием между параллельными прямыми.
54	Построение треугольника по трем элементам	Обобщить и систематизировать знания об отношениях фигур и их элементов Решают задачи на вычисление, доказательство и построение, проводят по ходу решения дополнительные построения
55	Решение задач. Задачи на построение	Обобщить и систематизировать знания об отношениях фигур и их элементов Анализируют и осмысливают текст задачи, моделируют условие с помощью схем, чертежей, реальных предметов, сопоставляют полученный результат с условием задачи.
56	Решение задач. Задачи на построение	Обобщить и систематизировать знания об отношениях фигур и их элементов Анализируют и осмысливают текст задачи, моделируют условие с помощью схем, чертежей, реальных предметов, в задачах на построение исследуют возможные случая.
57	Решение задач. Задачи на построение	Продемонстрировать уровень владения изученным материалом Распознают на чертежах геометрические фигуры и их элементы.  Решают задачи на доказательство и вычисление
58	Решение задач. Подготовка к контрольной работе	Обобщить и систематизировать знания об отношениях фигур и их элементов Анализируют и осмысливают текст задачи, моделируют условие с помощью схем, чертежей, реальных предметов, в задачах на построение исследуют возможные случая.
59	Контрольная работа №5 по теме «Соотношения между сторонами и углами треугольника.»	Продемонстрировать уровень владения изученным материалом Распознают на чертежах геометрические фигуры и их элементы.  Решают задачи на доказательство и вычисление
60	Анализ ошибок контрольной работы	Анализ ошибок
Повторение 8ч.
61	Повторение. Начальные геометрические сведения	Обобщить и систематизировать знания по теме: «Начальные геометрические сведения»
62	Повторение. Признаки равенства треугольников. Равнобедренный треугольник	Обобщить и систематизировать знания по теме: «Треугольники» Распознают на чертежах геометрические фигуры. Выделяют конфигурацию, необходимую для поиска решения задачи, используя определения, признаки и свойства выделяемых фигур или их отношений
63	Повторение.  Признаки равенства треугольников. Равнобедренный треугольник	Обобщить и систематизировать знания по теме: «Треугольники»
64	Повторение. Параллельные прямые	Обобщить и систематизировать знания по теме: «Параллельные прямые» Отражают условие задачи на чертежах. Выделяют конфигурацию, необходимую для поиска решения задачи, используя определения, признаки и свойства выделяемых фигур или их отношений
65	Повторение. Соотношения между сторонами и углами треугольника.	Обобщить и систематизировать знания по теме: «Соотношения между сторонами и углами треугольника»
66	Обобщение курса геометрии	Обобщить и систематизировать знания
67	Итоговый контрольный тест	Продемонстрировать уровень владения изученным материалом Распознают на чертежах геометрические фигуры и их элементы.  Решают задачи на доказательство и вычисление
68	Итоговый контрольный тест

 

 

 

 

 

 

 

 

 

 

 

 

КИМ

Контрольная работа №1 «Начальные геометрические сведения» (10 урок)

Вариант 1

1. Три точки В,С и D лежат на одной прямой. Известно, что ВD = 17 см, DС = 25 см. Какой может быть длина отрезка ВС?

2. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204^о. Найдите угол МОD.

3. С помощью транспортира начертите угол, равный 78^о, и проведите биссектрису смежного с ним угла.

Вариант 2

1. Три точки M, N, K  лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Какой может быть длина отрезка MK?

2. Сумма вертикальных углов AOB  и COD, образованных при пересечении прямых AD и BC, равна 108^о. Найдите угол BОD.

3. С помощью транспортира начертите угол, равный 132^о, и проведите биссектрису одного из  смежных с ним углов.

Контрольная работа №2 «Признаки равенства треугольников» ( 27 урок)

   Вариант 1

1. 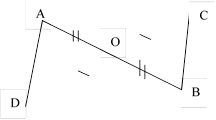       На рисунке отрезки АВ и СD имеют общую середину О. Докажите, что .

·          

 

 

 

 

 

 

 

 

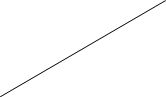2. Луч АD – биссектриса угла А. на сторонах угла А отмечены точки В и С так, что . Докажите, что АВ = АС.

3. Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ₁ к боковой стороне АС.

   Вариант 2

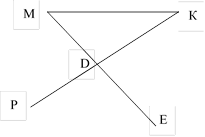1.  На рисунке отрезки МЕ и  РК точкой D делятся пополам . Докажите, что .

 

 

 

 

 

 

 

 

 

 

 

 

2. На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DР – биссектриса угла МDК.

3. Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла  А.

Контрольная работа №3 «Параллельные прямые» ( 40 урок)

 

Вариант 1

1.  Отрезки EF  и  PQ  пересекаются в их середине М.  Докажите, что РЕ║QF.

2. Отрезок DM – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DMN, если .

 

Вариант 2

1.  Отрезки MN и EF  пересекаются в их середине Р. Докажите, что ЕN║МF.

2. Отрезок АD – биссектриса треугольника АВС. Через точку D  проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если .

Контрольная работа №4 Соотношения между сторонами и углами треугольника(46 урок)

Вариант 1

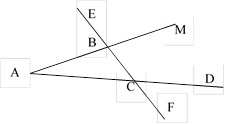1.  На рисунке , , АC = 12 см. Найдите сторону АВ треугольника АВС.

 

 

 

 

 

 

 

2. В треугольнике СDЕ  точка М лежит на стороне СЕ, причем угол СМD острый. Докажите, что DЕ > DМ.

3. Периметр равнобедренного  тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.

Вариант 2

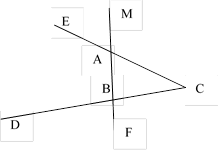1.  На рисунке , , BC = 9 см. Найдите сторону АC треугольника АВС.

 

 

 

 

 

 

 

 

2. В треугольнике MNP  точка K лежит на стороне MN, причем угол NKP острый. Докажите, что KP < МP.

3.Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.

Контрольная работа №5 «Прямоугольные треугольники»

Вариант 1

1.  В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найдите расстояние от точки О до прямой МN.

2. Постройте прямоугольный треугольник по гипотенузе и острому углу.

3. С помощью циркуля и линейки постройте угол, равный 150^о.

Вариант 2

1.  В прямоугольном треугольнике DCE c прямым углом С проведена биссектриса EF, причем FC = 13 см.  Найдите расстояние от точки F до прямой DE.

2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.

3. С помощью циркуля и линейки постройте угол, равный 105^о.

Итоговая контрольная работа (68 урок)

Вариант 1

1.  В равнобедренном треугольнике АВС с основанием АС на медиане ВD отмечена точка К, а на сторонах АВ и ВС – точки М и N соответственно. Известно, что

 а) Найдите угол BNK.

б)  Докажите, что прямые MN и ВК взаимно перпендикулярны.

2. На сторонах АВ, ВС и СА треугольника АВС отмечены точки D, E и F соответственно. Известно, что

а) Найдите угол DFE.

б)  Докажите, что прямые АВ и ЕF  пересекаются.

3. В прямоугольном треугольнике АВС катет АВ равен 3 см, угол С равен 15⁰.  На катете АС отмечена точка D так, что .

а)  Найдите длину отрезка ВD.

б)  Докажите, что ВC < 12 cм.

Вариант 2

1. В треугольнике АВС угол А равен 55^о. Внутри треугольника отмечена точка О так, что  и АО = ОС.

а)  Найдите угол АСВ.

б)  Докажите, что прямая  ВО является серединным  перпендикуляром к стороне АС.

2. На прямой последовательно отложены отрезки  АВ, ВС и СD.Точки Е и F расположены по разные стороны от этой прямой, причем 

Докажите, что:

а) прямые ВЕ и CF параллельны;

б)  прямые ВF и СЕ пересекаются.

3. В треугольнике АВС На стороне FС отмечена точка D так, что .

а)  Найдите длину отрезка АD.

б)  Докажите, что периметр треугольника АВС меньше 10 см.

 

 

 

Электронно методические комплекты:

1. Интернет-портал Всероссийской олимпиады школьников. – : http://www.rusolymp.ru

2. Всероссийские дистанционные эвристические олимпиады по математике. –: http://www.eidos.ru/olymp/mathem/index.htm

3. Информационно-поисковая система «Задачи». – : http://zadachi.mccme.ru/easy

4. Задачи: информационно-поисковая система задач по математике: http://zadachi.mccme.ru 

5. Конкурсные задачи по математике: справочник и методы решения –: http://mschool.kubsu.ru/cdo/shabitur/kniga/tit.htm

6. Материалы (полные тексты) свободно распространяемых книг по математике: http://www.mccme.ru/free-books

 

 

СТАРТОВЫЙ КОНТРОЛЬ

Стартовый контроль можно провести несколькими способами:

• предложить учащимся все задачи из списка для выполнения дома;
• выбрать несколько задач и предложить небольшую проверочную работу по повторению;
• разбить задачи на несколько групп и предлагать их для решения последовательно в течение нескольких уроков.

Форма стартового контроля выбирается учителем.

1) В равностороннем треугольнике со стороной 6см проведен отрезок, соединяющий середины двух сторон. Определите вид получившегося при этом треугольника и найдите его периметр.

2) Как построить центральный угол, вписанный угол?

3) Постройте острый угол, если его косинус равен .

4) Найдите площадь квадрата, если его диагональ равна 16см.

5) Выясните, является ли треугольник со сторонами 10, 24 и 26 прямоугольным?

6) Из точки А на прямую m опущен перпендикуляр АС = 15см. Наклонная АВ = 17см. Найдите проекцию этой наклонной на прямую m.

7) Диагональ параллелограмма образует с двумя его сторонами углы 25⁰ и 35⁰. Найдите углы параллелограмма.

8) Одна из сторон параллелограмма на 2 см больше другой, а его периметр равен 24см. Определите стороны параллелограмма.

9) Одна из его диагоналей ромба равна его стороне. Определите углы ромба.

10) В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 6см и 30см. Найдите основания трапеции.

11) В прямоугольном треугольнике АВС даны катет ВС = 8см и ÐА = 40⁰. Найдите катет АС, гипотенузу АВ и ÐВ.

12) Найдите катеты равнобедренного прямоугольного треугольника, если его гипотенуза равна 4см.

13) Прямая МК параллельна стороне АС треугольника АВС. Найдите ВК, если ВС = 12, МК = 8, АС = 15.

14) Диагональ прямоугольника равна 16см и образует с одной из его сторон угол 30⁰. Найдите площадь треугольника.

15) Прямоугольник вписан в окружность радиуса 5см. Одна из его сторон равна 8 см. Найдите другие стороны прямоугольника.

16) Диагонали ромба равны 10см и 24 см. Найдите длины его сторон.

17) Постройте:

а) ромб с заданными диагоналями;

б) параллелограмм по двум сторонам и углу между ними;

в) параллелограмм по стороне и двум диагоналям.

18) АВСD – трапеция с основаниями ВС и АD, О – точка пересечения диагоналей.

а) Докажите, что ∆ADO подобен ∆СВО.

б) Найдите основание ВС, если AD = 15см, ВО = 4см, DO = 5см.

19) Прямая, АС параллельна стороне DM, АК:DК = 5:6. Найдите площадь ∆ DКМ, если площадь ∆ АКС равна 175 см².

20) Из точки D, лежащей на гипотенузе АВ прямоугольного треугольника АВС, опущен перпендикуляр DE на катет ВС. Найдите АС, если ВС = 12, ВЕ = 8, DE = 6.

 

 

 

 

 

 

ИТОГОВЫЙ КОНТРОЛЬ

Тест состоит из двух частей. Каждая часть включает пять задач. При выполнении заданий первой части учащимся нужно выбрать один из четырех  предложенных ответов. При выполнении задач второй части учащиеся должны указать число, являющееся ответом данной задачи.

Часть I

1. Какое утверждение верно для треугольника со сторонами 5, 9, 15?

а) треугольник остроугольный;

б) треугольник тупоугольный;

в) треугольник прямоугольный;

г) такого треугольника не существует.

2. Если одна из сторон треугольника на 3 см меньше другой стороны, высота делит третью сторону на отрезки 5 см и 10 см, то периметр треугольника равен:

а) 25см;                                б) 40 см;

в) 32см;                                                г) 20 см.

3. Если один из углов ромба равен 60⁰, а диагональ, проведенная из вершины этого угла, равна 4 см, то периметр ромба равен:

а) 16 см;                                               б) 8 см;

в) 12 см;                                               г) 24 см.

4. Величина одного углов треугольника равна 20⁰. Найдите величину острого угла между биссектрисами двух других  углов треугольника.

а) 84⁰;                                                   б) 92⁰;

в) 80⁰;                                                   в) 87⁰.

5. В ∆ АВС сторона а = 7, сторона b = 8, сторона с = 5. Вычислите Ð А.

а) 120⁰;                                 б) 45⁰;

в) 30⁰;                                                   в) 60⁰.

Часть II

1.                 В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5,  считая от вершины, лежащей против основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.

2.                  В треугольнике ВСЕ Ð С = 60⁰, СЕ : ВС = 3 : 1. Отрезок СК – биссектриса треугольника. Найдите КЕ, если радиус описанной около треугольника окружности равен 8 см.

3.                  Найдите площадь треугольника КМР, если сторона КР равна 5, медиана РО равна 3, Ð КОР = 135⁰.

4.                  Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если ее средняя линия равна 5.

5.                  Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается катетов АС и ВС соответственно в точках  Е и D. Найдите величину угла АВС (в градусах), если известно, что АЕ = 1, ВD = 3.

Ответы к тесту

	Часть 1					Часть 2
№ задания	1	2	3	4	5	1	2	3	4	5
ответ	г	б	а	в	г	30	18	3	25	30

ПЕРЕЧЕНЬ ПРОВЕРОЧНЫХ РАБОТ ПО ГЛАВАМ

№	ТЕМА
1	Векторы. Метод координат.
2	Соотношения между сторонами и углами   треугольника.
3	Длина окружности,  площадь круга.
4	Движения.
5	Итоговая  контрольная работа.

ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ РАБОТ

№	ТЕМА
1	Правила действий над векторами.
2	Решение треугольников.
3	Правильные многоугольники.
4	Движения.
5	Повторение. Треугольники.
6	Повторение. Четырехугольники.
7	Повторение.  Окружности.
8	Повторение. Комбинированные задачи.

Практические работы не являются обязательными, они могут быть проведены в различных других формах: домашней контрольной работы, зачетной работы, самостоятельной работы, в виде теста и т.д.

КОМПЛЕКТ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ НА КОНЕЦ ГОДА

1	Приведите примеры векторных величин, известных вам из курса физики.
2	Дайте определение вектора. Объясните, какой вектор называется нулевым.
3	Какие векторы называются коллинеарными? сонаправленными?  противоположно направленными?
4	Дайте определение равных векторов.
5	Объясните, какой вектор называется суммой двух векторов? В чем заключается правило треугольника сложения двух векторов? правило параллелограмма? правило многоугольника для сложения нескольких векторов?
6	Сформулируйте и докажите теорему о законах сложения векторов.
7	Какой вектор называется разностью двух векторов? Постройте разность двух данных векторов.
8	Какой вектор называется противоположным данному? Сформулируйте и докажите теорему о разности векторов.
9	Какой вектор называется произведением вектора на число?
10	Сформулируйте основные свойства умножения векторов на число.
11	Приведите примеры применения векторов к решению задач.
12	Какой отрезок называется средней линией треугольника.
13	Сформулируйте и докажите теорему о средней линии треугольника.
14	Сформулируйте и докажите лемму о коллинеарных векторах.
15	Что значит разложить вектор по двум данным векторам?
16	Сформулируйте и докажите утверждение о разложении вектора по двум неколлинеарным векторам.
17	Что такое координаты вектора? Сформулируйте и докажите правила нахождения координат суммы и  разности векторов, а также произведения вектора на число по заданным координатам векторов.
18	Что такое радиус-вектор точки?
19	Выведите формулы для вычисления координат вектора по координатам его начала и конца.
20	Выведите формулу для вычисления координат середины  отрезка по координатам его концов.
21	Выведите формулу для вычисления длины вектора по его координатам.
22	Выведите формулу для вычисления расстояния между двумя точками по их координатам.
23	Выведите уравнение окружности данного радиуса с центром в данной точке.
24	Напишите уравнение окружности данного радиуса с центром в начале координат.
25	Выведите уравнение данной прямой в прямоугольной системе координат.
26	Напишите уравнения прямых, проходящих через данную точку М0(x0;y0)  параллельных началам координат.
27	Напишите уравнения осей координат.
28	Объясните, что такое синус, косинус и тангенс угла. Докажите основное тригонометрическое тождество.
29	Напишите формулы приведения.
30	Сформулируйте и докажите теорему о площади треугольника (по двум сторонам и синусу угла между ними).
31	Сформулируйте и докажите теорему синусов.
32	Сформулируйте и докажите теорему косинусов.
33	Что означает решить треугольник? Сформулируйте три основные задачи  на решение треугольника и объясните, как они решаются.
34	Какие два вектора называются перпендикулярными?
35	Что такое скалярное произведение векторов? Сформулируйте и докажите свойства скалярного произведения векторов.
36	Запишите условие перпендикулярности двух векторов с заданными координатами..
37	Какой многоугольник называется правильным? Приведите примеры правильных многоугольников.
38	Запишите  формулу для вычисления угла правильного n-угольника.
39	Сформулируйте и докажите теоремы об окружности,  вписанной и описанной около правильного многоугольника.
40	Запишите формулу для вычисления стороны правильного n-угольника и  радиуса вписанной в него окружности через радиус описанной окружности.
41	Запишите формулу для вычисления площади правильного многоугольника через его периметр и радиус вписанной окружности.
42	Как выражаются стороны правильного треугольника, квадрата и правильного шестиугольника через радиус описанной окружности.
43	Запишите формулы для вычисления длины окружности, площади круга, площади кругового сектора.
44	Объясните, что такое отображение плоскости на себя.
45	Какое отображение плоскости на себя называется осевой симметрией? центральной симметрией?
46	Что такое движение (или перемещение) плоскости?
47	Объясните, что такое наложение.
48	Какое отображение плоскости на себя называется параллельным переносом?
49	Какое отображение плоскости на себя называется поворотом?

 

 

Используемые формы, способы и средства проверки и оценки образовательных результатов

Оценка знаний–систематический процесс, который состоит в определении степени соответствия имеющихся знаний, умений, навыков, предварительно планируемым. Процесс оценки включает в себя такие компоненты: определение целей обучения; выбор контрольных заданий, проверяющих достижение этих целей; отметку или другой способ выражения результатов проверки. В зависимости от поставленных целей по-разному строится программа контроля, подбираются различные типы вопросов и заданий. Но применение примерных норм оценки знаний должно внести единообразие в оценку знаний и умений учащихся и сделать ее более объективной. Примерные нормы представляют основу, исходя из которой, учитель оценивает знания и умения учащихся.

Содержание и объем материала, подлежащего проверке и оценке, определяются программой по математике для основной  школы. В задания для проверки включаются основные, типичные и притом различной сложности вопросы, соответствующие проверяемому разделу программы.

Основными формами проверки знаний и умений учащихся по математике в основной школе являются  опрос, экзамен, зачет, контрольная работа, самостоятельная работа, тестирование, проверочная работа, проверка письменных домашних работ наряду с которыми применяются и другие формы проверки. При этом учитывается, что в некоторых случаях только устный опрос может дать более полные представления о знаниях и умениях учащихся; в тоже время письменная работа позволяет оценить умение учащихся излагать свои мысли на бумаге; навыки грамотного оформления выполняемых ими заданий.

При оценке устных ответов и письменных работ учитель в первую очередь учитывает имеющиеся у учащегося фактические знания и умения, их полноту, прочность, умение применять на практике в различных ситуациях. Результат оценки зависит также от наличия и характера допущенных погрешностей.

Среди погрешностей выделяются ошибки, недочеты и мелкие погрешности.

Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями и их применением.

К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в соответствии с программой основными. К недочетам относятся погрешности, объясняющиеся рассеянностью или недосмотром, но которые не привели к искажению смысла полученного учеником задания или способа его выполнения. Грамматическая ошибка, допущенная в написании известного учащемуся математического термина, небрежная запись, небрежное выполнение чертежа считаются недочетом.

К мелким погрешностям относятся погрешности в устной и письменной речи, не искажающие смысла ответа или решения, случайные описки и т. п.

Каждое задание для устного опроса или письменной работы представляет теоретический вопрос или задачу.

Ответ на вопрос считается безупречным, если его содержание точно соответствует вопросу, включает все необходимые теоретические сведения, обоснованные заключения и поясняющие примеры, а его изложение и оформление отличаются краткостью и аккуратностью.

Решение задачи считается безупречным, если получен верный ответ при правильном ходе решения, выбран соответствующий задаче способ решения, правильно выполнены необходимые вычисления и преобразования, последовательно и аккуратно оформлено решение.

Оценка ответа учащегося при устном опросе и оценка письменной контрольной работы проводится по пятибалльной системе.

Оценка устных ответов:

Ответ оценивается отметкой “5”, если учащийся:

·         полностью раскрыл содержание материала в объеме, предусмотренном программой и учебником;

·         изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

·         правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

·         показал умение иллюстрировать теорию конкретными примерами, применять в новой ситуации при выполнении практического задания;

·         продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;

·         отвечал самостоятельно, без наводящих вопросов учителя.

Ответ оценивается отметкой “4”,

если удовлетворяет в основном требованиям на оценку “5”, но при этом имеет один из недочетов:

·         в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

·         допущены 1-2 недочета при освещении основного содержания ответа, исправленные после замечания учителя;

·         допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.)

Ответ оценивается отметкой “3”, если:

·         неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программы;

·         имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

·         ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил обязательное задание.

Ответ оценивается отметкой “2”, если:

·         не раскрыто содержание учебного материала;

·         обнаружено незнание или не понимание учеником большей или наиболее важной части учебного материала;

·         допущены ошибки в определении понятия, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Оценивание письменных работ:

При проверке письменных работ по математике следует различать грубые и негрубые ошибки.

                К грубым ошибкам относятся:

·         -вычислительные ошибки в примерах и задачах;

·         -ошибки на незнание порядка выполнения арифметических действий;

·         -неправильное решение задачи (пропуск действий, неправильный выбор действий, лишнее действие);

·         -недоведение до конца решения задачи или примера;

·         -невыполненное задание.

                К негрубым ошибкам относятся:

·         -нерациональные приемы вычислений;

·         - неправильная постановка вопроса к действию при решении задачи;

·         -неверно сформулированный ответ задачи;

·         -неправильное списывание данных чисел, знаков;

·         -недоведение до конца преобразований.

При оценке письменных  работ ставятся следующие отметки:

“5”- если задачи решены без ошибок;

“4”- если допущены 1-2 негрубые ошибки;

“3”- если допущены 1 грубая и 3-4 негрубые ошибки;

“2”- незнание основного программного материала или отказ от выполнения учебных обязанностей.

Оценивание тестовых работ:

“5”- если набрано от 81до100% от максимально возможного балла;

“4”- от 61до 80%;

“3”- от 51 до 60%;

“2”- до 50%