
Тетрадь подготовки к ОГЭ
Ученика(цы) ________________
Школа _____
Преподаватель:
Григорьева Вера Анатольевна
Задание №1
1. Задание 1 № 314127Найдите значение выражения 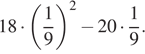
2. Задание 1 № 314264Вычислите: ![]()
Ответ:
3. Задание 1 № 314265Вычислите: ![]()
Ответ:
4. Задание 1 № 314288Найдите значение выражения
![]()
Ответ:
5. Задание 1 № 333006Найдите значение выражения ![]() .
.
Ответ:
6. Задание 1 № 333111Найдите значение выражения ![]() .
.
Ответ:
7. Задание 1 № 337273Найдите значение выражения ![]()
Ответ:
8. Задание 1 № 337375Найдите значение выражения ![]()
Ответ:
9. Задание 1 № 337385Найдите значение выражения ![]()
Ответ:
10. Задание 1 № 33750Найдите значение
выражения ![]()
Ответ:
11. Задание 1 № 33752Найдите значение
выражения ![]()
Ответ:
12. Задание 1 № 34058Найдите значение выражения ![]()
Ответ:
13. Задание 1 № 34166Найдите значение выражения 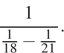
Ответ:
1. Задание 1 № 188айдите значение выражения
![]()
Ответ:
2. Задание 1 № 314Найдите значение выражения ![]()
Ответ:
3. Задание 1 № 337Найдите значение выражения ![]()
Ответ:
4. Задание 1 № 337Найдите значение выражения ![]()
Ответ:
5. Задание 1 № 314Найдите значение выражения ![]()
Ответ:
6. Задание 1 № 287Найдите значение выражения ![]() .
.
Ответ:
7. Задание 1 № 314Найдите значение выражения ![]()
Ответ:
8. Задание 1 № 316Найдите значение
выражения: ![]()
Ответ:
9. Задание 1 № 316Найдите значение
выражения: ![]()
Ответ:
10. Задание 1 № 33Найдите значение выражения 0,007 · 7 · 700.
Ответ:
11. Задание 1 № 20Для каждой десятичной дроби укажите ее разложение в сумму разрядных слагаемых.
Номера запишите без пробелов, запятых и других дополнительных символов.
|
А. 0,7041 |
Б. 0,7401 |
В. 7,401 |
|
|
1) |
2) |
||
|
3) |
4) |
||
1. Задание 1 № 110Найдите значение выражения
![]()
Ответ:
2. Задание 1 № 136Найдите значение выражения
![]()
Ответ:
3. Задание 1 № 203Запишите в ответе номера тех выражений, значение которых равно 0.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
|
1) |
2) |
3) |
4) |
Ответ:
4. Задание 1 № 203Запишите в ответе номера тех выражений, значение которых равно −5.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
|
1) |
2) |
3) |
4) |
Ответ:
5. Задание 1 № 203Запишите десятичную
дробь, равную сумме ![]() .
.
Ответ:
6. Задание 1 № 311395Найдите значение выражения
![]() .
.
Ответ:
7. Задание 1 № 314132Найдите значение выражения ![]()
Ответ:
8. Задание 1 № 314144Найдите значение выражения ![]()
Ответ:
9. Задание 1 № 314204Найдите значение выражения ![]()
Ответ:
10. Задание 1 № 31420Найдите значение выражения ![]()
11. Задание 1 № 31420Найдите значение выражения ![]()
Ответ:
12. Задание 1 № 31421Найдите значение выражения ![]()
Ответ:
13. Задание 1 № 31421Найдите значение выражения ![]()
Ответ:
14. Задание 1 № 31422Найдите значение выражения ![]()
Ответ:
15. Задание 1 № 31422Найдите значение выражения ![]()
Ответ:
16. Задание 1 № 314237Найдите значение выражения ![]()
Ответ:
17. Задание 1 № 314242Найдите значение выражения ![]()
Ответ:
18. Задание 1 № 337268Найдите значение выражения ![]()
Ответ:
19. Задание 1 № 337295Найдите значение выражения ![]()
Ответ:
20. Задание 1 № 337318Найдите значение выражения ![]()
Ответ:
21. Задание 1 № 337402Найдите значение выражения ![]()
Ответ:
22. Задание 1 № 338038Найдите значение выражения (4,9 · 10− 3)(4 · 10− 2).
Ответ:
23. Задание 1 № 341487Найдите значение выражения ![]()
1. Задание 1 № 203739
Укажите выражение, значение которого является наименьшим.
|
1) |
2) |
3) |
4) |
Ответ:
2. Задание 1 № 203741Запишите в ответе номера верных равенств.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
|
1) |
2) |
3) |
4) |
Ответ:
3. Задание 1 № 203742Каждому выражению поставьте в соответствие его значение:
|
А. |
Б. |
В. |
|
1) 3,2 |
2) 1,75 |
3) 0,45 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
4. Задание 1 № 203743Запишите в ответе номера выражений, значения которых положительны.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
|
1) |
2) |
3) |
4) |
Ответ:
5. Задание 1 № 203746Соотнесите обыкновенные дроби с равными им десятичными.
|
А. |
Б. |
В. |
Г. |
|
1) 0,5 |
2) 0,02 |
3) 0,12 |
4) 0,625 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
|
|
|
|
|
6. Задание 1 № 287932Расположите в порядке возрастания числа 0,1439; 1,3; 0,14.
|
1) 0,1439; 0,14; 1,3 |
2) 1,3; 0,14; 0,1439 |
3) 0,1439; 1,3; 0,14 |
4) 0,14; 0,1439; 1,3 |
Ответ:
7. Задание 1 № 287933Расположите в порядке убывания числа 0,1327; 0,014; 0,13.
|
1) 0,1327; 0,014; 0,13 |
2) 0,014; 0,13; 0,1327 |
3) 0,1327; 0,13; 0,014 |
4) 0,13; 0,014; 0,1327 |
8. Задание 1 № 287936Расположите в порядке
возрастания: ![]()
![]()
![]()
|
1) |
2) |
|
3) |
4) |
Ответ:
9. Задание 1 № 287937Расположите в порядке
убывания: ![]()
![]()
![]()
|
1) |
2) |
|
3) |
4) |
Ответ:
10. Задание 1 № 287939Укажите наибольшее из следующих чисел:
|
1) |
2) |
3) |
4) |
11. Задание 1 № 287940Укажите наименьшее из следующих чисел:
|
1) |
2) |
3) |
4) |
12. Задание 1 № 311948Укажите выражения, значения которых равны 0,25.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
|
1) |
2) |
|
3) |
4) |
Ответ:
13. Задание 1 № 353058Какому из данных промежутков
принадлежит число ![]() ?
?
|
1) [0,4; 0,5] |
2) [0,5; 0,6] |
3) [0,6; 0,7] |
4) [0,7; 0,8] |
1.Найдите значение выражения ![]()
2.Найдите значение выражения ![]() .
.
3. Найдите значение выражения ![]() .
.
4. Найдите значение выражения ![]() .
.
5. Найдите значение выражения ![]() .
.
6. Найдите значение выражения ![]() .
.
7.Найдите значение выражения ![]() .
.
1. Укажите выражение, значение которого является наименьшим.
|
1. |
|
2. |
|
3. |
|
4. |
|
2. Укажите выражение, значение которого является наименьшим.
3. Укажите выражение, значение которого является наименьшим.
4. Укажите выражение, значение которого является наименьшим.
5. Укажите выражение, значение которого является наименьшим.
6. Укажите выражение, значение которого является наименьшим.
7. Укажите выражение, значение которого является наименьшим.
8. Укажите выражение, значение которого является наименьшим
9. Укажите выражение, значение которого является наименьшим.
1. Какому из
выражений равно произведение
2. Какому из
выражений равно произведение
3. Какому из
выражений равно произведение
4. Какому из
выражений равно произведение
5. Какому из
выражений равно произведение
6. Какому из
выражений равно произведение
7. Какому из
выражений равно произведение
8. Какому из
выражений равно произведение
|
3. |
|
4. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Запишите в ответе номера верных равенств.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Запишите в ответе номера верных равенств.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3. Запишите в ответе номера верных равенств.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4. Запишите в ответе номера верных равенств.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5. Запишите в ответе номера верных равенств.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6. Запишите в ответе номера верных равенств.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7. Запишите в ответе номера верных равенств.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Запишите в ответе номера верных равенств.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
9. Запишите в ответе номера верных равенств.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
1. Для каждой десятичной дроби укажите ее разложение в сумму разрядных слагаемых.
А. 0,7407 Б. 7,4007 В. 0,7047
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
2. Для каждой десятичной дроби укажите ее разложение в сумму разрядных слагаемых.
А. 0,8402 Б. 8,4002 В. 0,8042
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
3. Для каждой десятичной дроби укажите ее разложение в сумму разрядных слагаемых.
А. 0,0573 Б. 0,5073 В. 0,5703
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
4. Для каждой десятичной дроби укажите ее разложение в сумму разрядных слагаемых.
А. 0,8014 Б. 8,1004 В. 0,8104
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
5. Для каждой десятичной дроби укажите ее разложение в сумму разрядных слагаемых.
А. 0,4013 Б. 4,1003 В. 0,4103
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
Здание №2
1. Задание 2 № 311294
Бабушка, живущая в Краснодаре, отправила 1 сентября четыре посылки своим внукам, живущим в разных городах России. В таблице дано контрольное время в сутках, установленное для пересылки посылок наземным транспортом (без учёта дня приёма) между некоторыми городами России.
|
Пункт отправки |
Пункт назначения |
||||
|
Архангельск |
Астрахань |
Барнаул |
Белгород |
Краснодар |
|
|
Архангельск |
9 |
12 |
7 |
10 |
|
|
Астрахань |
9 |
11 |
8 |
8 |
|
|
Барнаул |
12 |
11 |
11 |
12 |
|
|
Белгород |
8 |
8 |
13 |
9 |
|
|
Краснодар |
10 |
9 |
14 |
9 |
Какая из данных посылок не была доставлена вовремя?
В ответе укажите номер правильного варианта.
1) пункт назначения — Белгород, посылка доставлена 10 сентября
2) пункт назначения — Астрахань, посылка доставлена 12 сентября
3) пункт назначения — Барнаул, посылка доставлена 15 сентября
4) пункт назначения — Архангельск, посылка доставлена 11 сентября
2. Задание 2 № 311295
Для квартиры площадью 50 м2 заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.
|
Цвет потолка |
Цена (в руб.) за 1 м |
|
||
|
до 10 м |
от 11 до 30 м |
от 31 до 60 м |
свыше 60 м |
|
|
Белый |
1050 |
850 |
700 |
600 |
|
Цветной |
1200 |
1000 |
950 |
850 |
Какова стоимость заказа, если действует сезонная скидка в 10%?
В ответе укажите номер правильного варианта.
1) 35 000 руб. 2) 3 500 руб. 3) 34 990 руб. 4) 31 500 руб.
3. Задание 2 № 311297
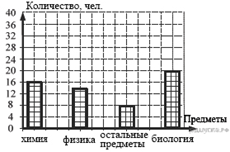 Завуч школы подвел
итоги по выбору предметов для сдачи ЕГЭ учащимися 11-х классов. Результаты
представлены на диаграмме. Сколько примерно учащихся выбрали для сдачи ЕГЭ
физику?
Завуч школы подвел
итоги по выбору предметов для сдачи ЕГЭ учащимися 11-х классов. Результаты
представлены на диаграмме. Сколько примерно учащихся выбрали для сдачи ЕГЭ
физику?
В ответе укажите номер правильного варианта.
1) 16 2) 12 3) 14 4) 8
1. Задание 2 № 30 В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.
|
|
Мальчики |
Девочки |
||||
|
Отметка |
«5» |
«4» |
«3» |
«5» |
«4» |
«3» |
|
Время, секунды |
4,6 |
4,9 |
5,3 |
5,0 |
5,5 |
5,9 |
Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?
В ответе укажите номер правильного варианта.
1) Отметка «5». 2) Отметка «4». 3) Отметка «3». 4) Норматив не выполнен.
2. Задание 2 № 160В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
|
Вещество |
Дети от 1 года до 14 лет |
Мужчины |
Женщины |
|
Жиры |
40−97 |
70−154 |
60−102 |
|
Белки |
36−87 |
65−117 |
58−87 |
|
Углеводы |
170−420 |
257−586 |
|
Какой вывод о суточном потреблении жиров 8-летним мальчиком можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 90 г жиров?
В ответе укажите номер правильного варианта.
1) Потребление в норме. 2) Потребление выше рекомендуемой нормы.
3) Потребление ниже рекомендуемой нормы. 4) В таблице недостаточно данных.
3. Задание 2 № 311292Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 65,8 г.
|
Категория |
Масса одного яйца, г |
|
Высшая |
75,0 и выше |
|
Отборная |
65,0 − 74,9 |
|
Первая |
55,0 − 64,9 |
|
Вторая |
45,0 — 54,9 |
|
Третья |
35,0 — 44,9 |
В ответе укажите номер правильного варианта.
1) Высшая 2) Отборная 3) Первая 4) Вторая
4. Задание 2 № 311293В таблице приведены нормативы по бегу на лыжах на 1 км для 10 класса.
|
|
мальчики |
девочки |
||||
|
Отметка |
«3» |
«4» |
«5» |
«3» |
«4» |
«5» |
|
Время (мин. и сек.) |
5:30 |
5:00 |
4:40 |
7:10 |
6:30 |
6:00 |
Какую отметку получит девочка, пробежавшая на лыжах 1 км за 6 минут 15 секунд?
В ответе укажите номер правильного варианта.
1) Неудовлетворительно 2) «4» 3) «3» 4) «5»
5. Задание 2 № 311427В таблице представлены нормативы по технике чтения в 3 классе.
|
Отметка |
Количество прочитанных слов минуту |
|
|
Первое полугодие учебного года |
Второе полугодие учебного года |
|
|
«2» |
59 и менее |
69 и менее |
|
«3» |
60−69 |
70−79 |
|
«4» |
70−79 |
80−89 |
|
«5» |
89 и более |
99 и более |
Какую отметку получит третьеклассник, прочитавший в апреле 68 слов за минуту?
В ответе укажите номер правильного варианта.
1) «2» 2) «3» 3) «4» 4) «5»
6. Задание 2 № 311504В таблице приведены
результаты двух полуфинальных забегов на дистанцию 60 м. В финальном
забеге 6 участников. Из каждого полуфинала в финал выходят два
спортсмена, показавших первый и второй результаты. К ним добавляют еще
двух спортсменов, показавших лучшее время среди всех остальных участников
полуфиналов. Запишите в ответ номера
спортсменов, не попавших в финал.
Запишите в ответ номера
спортсменов, не попавших в финал.
7. Задание 2 № 316223В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России на 1 января 2013 года.
|
Превышение скорости, км/ч |
11 − 20 |
21 − 40 |
41 − 60 |
61 и более |
|
Размер штрафа, руб. |
100 |
300 |
1000 |
2500 |
Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 175 км/ч на участке дороги с максимальной разрешённой скоростью 110 км/ч?
В ответе укажите номер правильного варианта.
1) 100 рублей 2) 300 рублей 3) 1000 рублей 4) 2500 рублей
8. Задание 2 № 316365В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.
|
Мощность автомобиля (в л. с.*) |
Налоговая ставка (в руб. за л. с. в год) |
|
не более 70 |
0 |
|
71—100 |
12 |
|
101—125 |
25 |
|
126—150 |
35 |
|
151—175 |
45 |
|
176—200 |
50 |
|
201—225 |
65 |
|
226—250 |
75 |
|
свыше 250 |
150 |
*л. с. — лошадиная сила Сколько рублей должен заплатить владелец автомобиля мощностью 185 л. с. в качестве налога за один год?
В ответе укажите номер правильного варианта.
1) 45 2) 50 3) 8000 4) 9250
9. Задание 2 № 316592В таблице даны результаты забега мальчиков 8 класса на дистанцию 60 м. Зачет выставляется при условии, что показан результат не хуже 10,5 с.
|
Номер дорожки |
I |
II |
III |
IV |
|
Время (в с) |
10,6 |
9,7 |
10,1 |
11,4 |
Укажите номера дорожек, по которым бежали мальчики, получившие зачет.
В ответе укажите номер правильного варианта.
1) только I 2) только II 3) I, IV 4) II, III
10. Задание 2 № 31659В таблице приведены нормативы по прыжкам с места для учеников 11 класса.
|
|
Мальчики |
Девочки |
||||
|
Отметка |
«5» |
«4» |
«3» |
«5» |
«4» |
«3» |
|
Расстояние, см |
230 |
220 |
200 |
185 |
170 |
155 |
Какую оценку получит девочка, прыгнувшая на 167 см?
В ответе укажите номер правильного варианта.
1) «5» 2) «4» 3) «3» 4) «Неудовлетворительно»
11. Задание 2 № 31772В таблице даны результаты забега девочек 8 класса на дистанцию 60 м. Зачет выставляется при условии, что показан результат не хуже 10,8 с.
|
Номер дорожки |
I |
II |
III |
IV |
|
Время (в с) |
10,7 |
10,9 |
9,8 |
11,4 |
Укажите номера дорожек, по которым бежали девочки, не получившие зачет.
В ответе укажите номер правильного варианта.
1) только II 2) только III 3) II, IV 4) I, III
12. Задание 2 № 33311В таблице даны результаты забега мальчиков 8 класса на дистанцию 60 м. Зачет выставляется при условии, что показан результат не хуже 10,5 с.
|
Номер дорожки |
I |
II |
III |
IV |
|
Время (в с) |
10,3 |
10,6 |
11,0 |
9,1 |
Укажите номера дорожек, по которым бежали мальчики, получившие зачет.
В ответе укажите номер правильного варианта.
1) I, IV 2) II, III 3) только III 4) только IV
1. Задание 2 № 311290Дорожный знак, изображённый на рисунке, называется «Ограничение высоты». Его устанавливают перед мостами, тоннелями и прочими сооружениями, чтобы запретить проезд транспортного средства, габариты которого (с грузом или без груза) превышают установленную высоту.

Какому из данных транспортных средств этот знак запрещает проезд?
В ответе укажите номер правильного варианта.
1) молоковозу высотой 3770 мм 2) пожарному автомобилю высотой 3400 мм
3) автотопливозаправщику высотой 2900 мм 4) автоцистерне высотой 3350 мм
2. Задание 2 № 311423На схеме зала кинотеатра отмечены разной штриховкой места с различной стоимостью билетов, а черным закрашены забронированные места на некоторый сеанс.
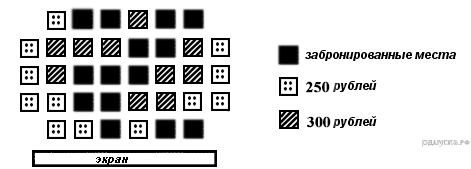
Сколько рублей заплатят за 5 билетов на этот сеанс пятеро друзей, если они хотят сидеть на одном ряду и выбирают самый дешевый вариант?
В ответе укажите номер правильного варианта.
1) 1300 2) 1250 3) 1350 4) 1500
3. Задание 2 № 311425В таблице представлены цены (в рублях) на некоторые товары в трёх магазинах:
|
Магазин |
Орехи (за кг.) |
Шоколад (за плитку) |
Зефир (за кг.) |
|
«Машенька» |
600 |
45 |
144 |
|
«Лидия» |
585 |
65 |
116 |
|
«Камея» |
660 |
53 |
225 |
Лариса Кузьминична хочет купить 0,4 кг орехов, 5 плиток шоколада и 1,5 кг зефира. В каком магазине стоимость такой покупки будет наименьшей, если в «Камее» проходит акция: скидка 20% на орехи и зефир, а в «Машеньке» скидка 10% на все продукты?
В ответе укажите номер правильного варианта.
1) В «Машеньке» 2) В «Лидии» 3) В «Камее» 4) Во всех магазинах стоимость покупки будет одинаковой
4. Задание 2 № 311429Бизнесмен Петров выезжает из Москвы в Санкт-Петербург на деловую встречу, которая назначена на 9:30. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.
|
Номер поезда |
Отправление из Москвы |
Прибытие в Санкт-Петербург |
|
038А |
00:43 |
08:45 |
|
020У |
00:53 |
09:02 |
|
016А |
01:00 |
08:38 |
|
116С |
01:00 |
09:06 |
Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят бизнесмену Петрову.
1) 038А 2) 020У 3) 016А 4) 116С
5. Задание 2 № 311511Платеж за потребление
электроэнергии осуществляется по двухтарифному счетчику. Тариф зависит
от времени суток. Общая сумма платежа складывается из сумм по каждому из
двух тарифов. Квитанция на оплату содержит следующую таблицу.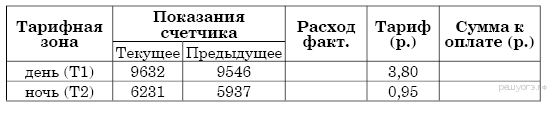 Вычислите общую сумму
платежа за указанный в таблице расход электроэнергии.
Вычислите общую сумму
платежа за указанный в таблице расход электроэнергии.
6. Задание 2 № 311945В таблице даны результаты олимпиад по истории и обществознанию в 10 «А» классе.
|
Номер ученика |
Балл по истории |
Балл по обществознанию |
|
5005 |
45 |
76 |
|
5006 |
34 |
23 |
|
5011 |
67 |
56 |
|
5015 |
78 |
67 |
|
5018 |
59 |
79 |
|
5020 |
46 |
32 |
|
5025 |
54 |
76 |
|
5027 |
95 |
88 |
|
5029 |
46 |
72 |
|
5032 |
83 |
45 |
|
5041 |
48 |
66 |
|
5042 |
28 |
42 |
|
5043 |
63 |
67 |
|
5048 |
92 |
83 |
|
5054 |
38 |
64 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 130 или хотя бы по одному предмету набрано не меньше 70 баллов. Сколько человек из 10 «А», набравших меньше 60 баллов по истории, получат похвальные грамоты?
В ответе укажите номер правильного варианта.
1) 5 2) 2 3) 3 4) 4
7. Задание 2 № 314126В таблице даны результаты забега мальчиков 8-го класса на дистанцию 60 м.
|
Номер дорожки |
1 |
2 |
3 |
4 |
|
Время (с) |
10,3 |
10,7 |
11,0 |
9,1 |
Зачёт выставляется, если показано время не хуже 10,5 с. Выпишите номера дорожек, по которым бежали мальчики, получившие зачёт.
8. Задание 2 № 315144Василий измерял в течение недели время, которое он тратил на дорогу до школы, а результаты записывал в таблицу.
|
День недели |
Пн |
Вт |
Ср |
Чт |
Пт |
Сб |
|
Время (мин.) |
28 |
38 |
27 |
37 |
25 |
25 |
Сколько минут в среднем занимает у Василия дорога до школы?
9. Задание 2 № 317678Для квартиры площадью 75 кв. м заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.
|
Цвет потолка |
Цена в рублях за 1 м2 (в зависмости от площали помещения) |
|||
|
до 10 м2 |
от 11 до 30 м2 |
от 31 до 60 м2 |
свыше 60 м2 |
|
|
белый |
1200 |
1000 |
800 |
600 |
|
цветной |
1350 |
1150 |
950 |
750 |
Какова стоимость заказа, если действует сезонная скидка в 5%?
В ответе укажите номер правильного варианта.
1) 4275 рублей 2) 45 000 рублей 3) 42 750 рублей 4) 44 995 рублей
10. Задание 2 № 33740В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет дальше всех от Солнца?
|
Планета |
Марс |
Меркурий |
Нептун |
Сатурн |
|
Расстояние (в км) |
2,280 · 108 |
5,790 · 107 |
4,497 · 109 |
1,427 · 109 |
В ответе укажите номер правильного варианта.
1) Марс 2) Меркурий 3) Нептун 4) Сатурн
11. Задание 2 № 33754В нескольких эстафетах, которые проводились в школе, команды показали следующие результаты:
|
Команда |
I эстафета, мин. |
II эстафета, мин. |
III эстафета, мин. |
IV эстафета, мин. |
|
«Непобедимые» |
3,0 |
5,6 |
2,8 |
6,8 |
|
«Прорыв» |
4,6 |
4,6 |
2,6 |
6,5 |
|
«Чемпионы» |
3,6 |
4,0 |
2,3 |
5,0 |
|
«Тайфун» |
3,9 |
5,3 |
2,0 |
5,1 |
За каждую эстафету команда получает количество баллов, равное занятому в этой эстафете месту, затем баллы по всем эстафетам суммируются. Какое итоговое место заняла команда «Чемпионы», если победителем считается команда, набравшая наименьшее количество очков?
В ответе укажите номер правильного варианта.
1) 1 2) 2 3) 3 4) 4
12. Задание 2 № 33765Население США составляет 3,2·108 человек, а площадь их территории равна 9,5·106 кв. км. Сколько в среднем приходится жителей на 1 кв. км?
В ответе укажите номер правильного варианта.
1) примерно 29,6 человека 2) примерно 3,37 человека 3) примерно 33,7 человека
4) примерно 2,96 человека
13. Задание 2 № 33772Площадь территории России составляет 1,7 · 107 км2, а Норвегии — 3,2⋅105 км2. Во сколько раз площадь территории России больше площади территории Норвегии?
1) примерно в 1,9 раза 2) примерно в 5,3 раза 3) примерно в 53 раза 4) примерно в 530 раз
14. Задание 2 № 33776В таблице приведена стоимость работ по покраске потолков.
|
Цвет потолка |
Цена в рублях за 1 м2 (в зависимости от площади помещения) |
|||
|
до 10 м2 |
от 11 до 30 м2 |
от 31 до 60 м2 |
свыше 60 м2 |
|
|
белый |
105 |
85 |
70 |
60 |
|
цветной |
120 |
100 |
90 |
85 |
Пользуясь данными, представленными в таблице, определите, какова будет стоимость работ, если площадь потолка 40 м2, потолок цветной и действует сезонная скидка в 10%. Ответ укажите в рублях.
15. Задание 2 № 33783В таблице даны результаты олимпиад по географии и биологии в 8 «А» классе.
|
Номер ученика |
Балл по географии |
Балл по биологии |
|
5005 |
69 |
36 |
|
5006 |
88 |
48 |
|
5011 |
53 |
34 |
|
5015 |
98 |
55 |
|
5018 |
44 |
98 |
|
5020 |
74 |
37 |
|
5025 |
66 |
83 |
|
5027 |
76 |
82 |
|
5029 |
79 |
98 |
|
5032 |
76 |
39 |
|
5041 |
69 |
72 |
|
5042 |
45 |
54 |
|
5043 |
45 |
72 |
|
5048 |
55 |
48 |
|
5054 |
84 |
68 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 120 или хотя бы по одному предмету набрано не меньше 65 баллов.
Сколько человек из 8 «А», набравших меньше 65 баллов по географии, получат похвальные грамоты?
1) 1 2) 3 3) 4 4) 2
16. Задание 2 № 33802В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет ближе всех к Солнцу?
|
Планета |
Нептун |
Юпитер |
Уран |
Венера |
|
Расстояние (в км) |
4,497 · 109 |
7,781 · 108 |
2,871 · 109 |
1,082 · 108 |
В ответе укажите номер правильного варианта.
1) Нептун 2) Юпитер 3) Уран 4) Венера
17. Задание 2 № 34086В таблице даны результаты олимпиад по математике и обществознанию в 8 «А» классе.
|
Номер ученика |
Балл по математике |
Балл по обществознанию |
|
5005 |
76 |
38 |
|
5006 |
58 |
54 |
|
5011 |
93 |
97 |
|
5015 |
96 |
60 |
|
5018 |
63 |
90 |
|
5020 |
73 |
78 |
|
5025 |
73 |
35 |
|
5027 |
90 |
53 |
|
5029 |
59 |
63 |
|
5032 |
85 |
37 |
|
5041 |
52 |
43 |
|
5042 |
36 |
55 |
|
5043 |
91 |
71 |
|
5048 |
85 |
33 |
|
5054 |
32 |
81 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 150 или хотя бы по одному предмету набрано не меньше 80 баллов. Сколько человек из 8 «А», набравших меньше 80 баллов по математике, получат похвальные грамоты?
1) 2 2) 4 3) 5 4) 3
18. Задание 2 № 34312В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.
|
|
Мальчики |
Девочки |
||||
|
Отметка |
«отл.» |
«хор.» |
«удовл.» |
«отл.» |
«хор.» |
«удовл.» |
|
Время, секунды |
4,6 |
4,9 |
5,3 |
5,0 |
5,5 |
5,9 |
Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?
1) Отлично 2) Хорошо 3) Удовлетворительно 4) Норматив не выполнен
19. Задание 2 № 34846В таблице даны результаты олимпиад по математике и биологии в 8 «А» классе.
|
Номер ученика |
Балл по математике |
Балл по биологии |
|
5005 |
32 |
40 |
|
5006 |
86 |
32 |
|
5011 |
76 |
67 |
|
5015 |
72 |
48 |
|
5018 |
76 |
75 |
|
5020 |
50 |
94 |
|
5025 |
76 |
77 |
|
5027 |
75 |
53 |
|
5029 |
61 |
53 |
|
5032 |
54 |
97 |
|
5041 |
32 |
51 |
|
5042 |
40 |
59 |
|
5043 |
63 |
31 |
|
5048 |
95 |
33 |
|
5054 |
40 |
66 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 120 или хотя бы по одному предмету набрано не меньше 65 баллов.
Сколько человек из 8 «А», набравших меньше 65 баллов по математике, получат похвальные грамоты?
1) 3 2) 2 3) 4 4) 1
20. Задание 2 № 34855В таблице даны результаты олимпиад по физике и биологии в 10 «А» классе.
|
Номер ученика |
Балл по физике |
Балл по биологии |
|
5005 |
40 |
63 |
|
5006 |
96 |
61 |
|
5011 |
36 |
70 |
|
5015 |
94 |
46 |
|
5018 |
34 |
50 |
|
5020 |
39 |
83 |
|
5025 |
87 |
70 |
|
5027 |
100 |
99 |
|
5029 |
63 |
75 |
|
5032 |
89 |
45 |
|
5041 |
57 |
79 |
|
5042 |
69 |
98 |
|
5043 |
57 |
83 |
|
5048 |
93 |
72 |
|
5054 |
63 |
69 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 120 или хотя бы по одному предмету набрано не меньше 65 баллов. Сколько человек из 10 «А», набравших меньше 65 баллов по физике, получат похвальные грамоты?
1) 6 2) 5 3) 4 4) 3
21. Задание 2 № 34863В таблице даны результаты олимпиад по русскому языку и биологии в 11 «А» классе.
|
Номер ученика |
Балл по русскому языку |
Балл по биологии |
|
5005 |
30 |
83 |
|
5006 |
94 |
90 |
|
5011 |
61 |
87 |
|
5015 |
38 |
81 |
|
5018 |
72 |
55 |
|
5020 |
96 |
55 |
|
5025 |
41 |
76 |
|
5027 |
63 |
82 |
|
5029 |
99 |
58 |
|
5032 |
71 |
35 |
|
5041 |
38 |
97 |
|
5042 |
97 |
60 |
|
5043 |
67 |
60 |
|
5048 |
34 |
90 |
|
5054 |
73 |
96 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 150 или хотя бы по одному предмету набрано не меньше 80 баллов. Сколько человек из 11 «А», набравших меньше 80 баллов по русскому языку, получат похвальные грамоты?
1) 6 2) 7 3) 5 4) 8
22. Задание 2 № 34871В таблице даны результаты олимпиад по математике и биологии в 9 «А» классе.
|
Номер ученика |
Балл по математике |
Балл по биологии |
|
5005 |
49 |
55 |
|
5006 |
98 |
56 |
|
5011 |
30 |
36 |
|
5015 |
96 |
50 |
|
5018 |
37 |
87 |
|
5020 |
58 |
74 |
|
5025 |
77 |
52 |
|
5027 |
94 |
68 |
|
5029 |
72 |
66 |
|
5032 |
72 |
83 |
|
5041 |
76 |
35 |
|
5042 |
83 |
45 |
|
5043 |
95 |
79 |
|
5048 |
78 |
63 |
|
5054 |
99 |
41 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 130 или хотя бы по одному предмету набрано не меньше 70 баллов. Сколько человек из 9 «А», набравших меньше 70 баллов по математике, получат похвальные грамоты?
1) 1 2) 3 3) 4 4) 2
23. Задание 2 № 34874В таблице даны результаты олимпиад по математике и обществознанию в 8 «А» классе.
|
Номер ученика |
Балл по математике |
Балл по обществознанию |
|
5005 |
76 |
38 |
|
5006 |
58 |
54 |
|
5011 |
93 |
97 |
|
5015 |
96 |
60 |
|
5018 |
63 |
90 |
|
5020 |
73 |
78 |
|
5025 |
73 |
35 |
|
5027 |
90 |
53 |
|
5029 |
59 |
63 |
|
5032 |
85 |
37 |
|
5041 |
52 |
43 |
|
5042 |
36 |
55 |
|
5043 |
91 |
71 |
|
5048 |
85 |
33 |
|
5054 |
32 |
81 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 150 или хотя бы по одному предмету набрано не меньше 80 баллов. Сколько человек из 8 «А», набравших меньше 80 баллов по математике, получат похвальные грамоты?
1) 2 2) 4 3) 5 4) 3
24. Задание 2 № 348866Население Франции
составляет ![]() человек,
а площадь её территории равна
человек,
а площадь её территории равна ![]() кв.км.
Сколько в среднем приходится жителей на 1 кв.км?
кв.км.
Сколько в среднем приходится жителей на 1 кв.км?
1) примерно 8,73 человека 2) примерно 114,5 человека
3) примерно 87,3 человека 4) примерно 11,45 человека
25. Задание 2 № 349026В таблице даны результаты олимпиад по математике и биологии в 11 «А» классе.
|
Номер ученика |
Балл по математике |
Балл по биологии |
|
5005 |
37 |
65 |
|
5006 |
55 |
52 |
|
5011 |
75 |
45 |
|
5015 |
41 |
59 |
|
5018 |
47 |
75 |
|
5020 |
53 |
89 |
|
5025 |
51 |
67 |
|
5027 |
87 |
85 |
|
5029 |
60 |
69 |
|
5032 |
81 |
77 |
|
5041 |
49 |
47 |
|
5042 |
56 |
33 |
|
5043 |
32 |
66 |
|
5048 |
96 |
94 |
|
5054 |
70 |
53 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 110 или хотя бы по одному предмету набрано не меньше 60 баллов.Сколько человек из 11 «А», набравших меньше 60 баллов по математике, получат похвальные грамоты?
1) 4 2) 5 3) 6 4) 7
26. Задание 2 № 349035В таблице даны результаты олимпиад по физике и обществознанию в 11 «А» классе.
|
Номер ученика |
Балл по физике |
Балл по обществознанию |
|
5005 |
42 |
78 |
|
5006 |
88 |
41 |
|
5011 |
90 |
51 |
|
5015 |
79 |
79 |
|
5018 |
41 |
47 |
|
5020 |
66 |
78 |
|
5025 |
44 |
80 |
|
5027 |
73 |
69 |
|
5029 |
30 |
95 |
|
5032 |
92 |
40 |
|
5041 |
51 |
83 |
|
5042 |
69 |
87 |
|
5043 |
68 |
48 |
|
5048 |
86 |
59 |
|
5054 |
77 |
40 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 120 или хотя бы по одному предмету набрано не меньше 65 баллов. Сколько человек из 11 «А», набравших меньше 65 баллов по физике, получат похвальные грамоты?
1) 2 2) 4 3) 1 4) 3
27. Задание 2 № 349087В таблице даны результаты олимпиад по русскому языку и биологии в 8 «А» классе.
|
Номер ученика |
Балл по русскому языку |
Балл по биологии |
|
5005 |
45 |
36 |
|
5006 |
83 |
51 |
|
5011 |
49 |
56 |
|
5015 |
46 |
31 |
|
5018 |
35 |
37 |
|
5020 |
31 |
85 |
|
5025 |
48 |
60 |
|
5027 |
87 |
82 |
|
5029 |
92 |
41 |
|
5032 |
62 |
34 |
|
5041 |
64 |
48 |
|
5042 |
56 |
65 |
|
5043 |
73 |
84 |
|
5048 |
35 |
31 |
|
5054 |
54 |
88 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 110 или хотя бы по одному предмету набрано не меньше 60 баллов. Сколько человек из 8 «А», набравших меньше 60 баллов по русскому языку, получат похвальные грамоты?
1) 3 2) 2 3) 4 4) 1
28. Задание 2 № 349293В таблице даны результаты олимпиад по математике и биологии в 10 «А» классе.
|
Номер ученика |
Балл по математике |
Балл по биологии |
|
5005 |
69 |
30 |
|
5006 |
72 |
71 |
|
5011 |
32 |
95 |
|
5015 |
39 |
82 |
|
5018 |
58 |
52 |
|
5020 |
31 |
65 |
|
5025 |
87 |
76 |
|
5027 |
87 |
73 |
|
5029 |
84 |
32 |
|
5032 |
67 |
85 |
|
5041 |
72 |
86 |
|
5042 |
69 |
83 |
|
5043 |
46 |
34 |
|
5048 |
71 |
49 |
|
5054 |
49 |
51 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 140 или хотя бы по одному предмету набрано не меньше 75 баллов. Сколько человек из 10 «А», набравших меньше 75 баллов по математике, получат похвальные грамоты?
1) 4 2) 7 3) 5 4) 6
29. Задание 2 № 349461В таблице даны результаты олимпиад по географии и биологии в 11 «А» классе.
|
Номер ученика |
Балл по географии |
Балл по биологии |
|
5005 |
33 |
39 |
|
5006 |
55 |
45 |
|
5011 |
48 |
90 |
|
5015 |
35 |
53 |
|
5018 |
73 |
52 |
|
5020 |
79 |
87 |
|
5025 |
33 |
80 |
|
5027 |
40 |
93 |
|
5029 |
41 |
38 |
|
5032 |
93 |
95 |
|
5041 |
87 |
82 |
|
5042 |
38 |
85 |
|
5043 |
99 |
64 |
|
5048 |
79 |
31 |
|
5054 |
67 |
34 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 120 или хотя бы по одному предмету набрано не меньше 65 баллов. Сколько человек из 11 «А», набравших меньше 65 баллов по географии, получат похвальные грамоты?
1) 3 2) 4 3) 2 4) 5
30. Задание 2 № 349543В таблице даны результаты олимпиад по географии и биологии в 10 «А» классе.
|
Номер ученика |
Балл по географии |
Балл по биологии |
|
5005 |
60 |
66 |
|
5006 |
88 |
62 |
|
5011 |
64 |
80 |
|
5015 |
66 |
86 |
|
5018 |
83 |
76 |
|
5020 |
88 |
59 |
|
5025 |
84 |
79 |
|
5027 |
84 |
76 |
|
5029 |
98 |
90 |
|
5032 |
40 |
46 |
|
5041 |
75 |
45 |
|
5042 |
46 |
63 |
|
5043 |
43 |
70 |
|
5048 |
58 |
55 |
|
5054 |
60 |
100 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 150 или хотя бы по одному предмету набрано не меньше 80 баллов. Сколько человек из 10 «А», набравших меньше 80 баллов по географии, получат похвальные грамоты?
1) 3 2) 2 3) 4 4) 5
31. Задание 2 № 350235В таблице даны результаты олимпиад по географии и биологии в 11 «А» классе.
|
Номер ученика |
Балл по географии |
Балл по биологии |
|
5005 |
97 |
76 |
|
5006 |
44 |
84 |
|
5011 |
60 |
36 |
|
5015 |
65 |
82 |
|
5018 |
47 |
94 |
|
5020 |
61 |
74 |
|
5025 |
45 |
93 |
|
5027 |
93 |
43 |
|
5029 |
88 |
30 |
|
5032 |
36 |
81 |
|
5041 |
67 |
91 |
|
5042 |
37 |
32 |
|
5043 |
100 |
62 |
|
5048 |
65 |
75 |
|
5054 |
42 |
91 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 150 или хотя бы по одному предмету набрано не меньше 80 баллов. Сколько человек из 11 «А», набравших меньше 80 баллов по географии, получат похвальные грамоты?
1) 6 2) 7 3) 5 4) 8
Задание №3
1. Задание 3 № 205771О числах ![]() и
и ![]() известно,
что
известно,
что ![]() .
Среди приведенных ниже неравенств выберите верные:
.
Среди приведенных ниже неравенств выберите верные:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) Верно 1, 2 и 3
4) Верно 1, 2 и 3
2. Задание 3 № 205773На координатной прямой
изображены числа ![]() и
и ![]() .
Какое из следующих неравенств неверно?
.
Какое из следующих неравенств неверно?
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3. Задание 3 № 205775Какое из следующих
неравенств не следует из неравенства ![]() ?
?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4. Задание 3 № 311306Известно, что ![]() .
Какое из указанных утверждений верно?
.
Какое из указанных утверждений верно?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5. Задание 3 № 311418На координатной прямой
отмечено число ![]() .
Какое из утверждений относительно этого числа является верным?
.
Какое из утверждений относительно этого числа является верным?
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6. Задание 3 № 311422На координатной прямой
изображены числа ![]() и
и ![]() .
Какое из следующих неравенств неверно?
.
Какое из следующих неравенств неверно?
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7. Задание 3 № 311749На координатной прямой отмечено число а.
![]() Какое из утверждений
относительно этого числа является верным?
Какое из утверждений
относительно этого числа является верным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Задание 3 № 311779На координатной прямой отмечено число а.
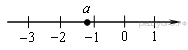
Какое из утверждений относительно этого числа является верным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
9. Задание 3 № 311805На координатной прямой отмечено число а.
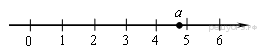
Какое из утверждений относительно этого числа является верным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
10. Задание 3 № 311837На координатной прямой отмечено число а.
![]()
Какое из утверждений относительно этого числа является верным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
11. Задание 3 № 314789На координатной прямой отмечены числа а и с. Какое из следующих утверждений неверно?
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
12. Задание 3 № 314800На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?
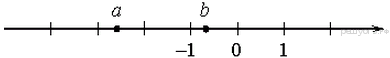
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
13. Задание 3 № 316220На координатной прямой
отмечено число ![]()
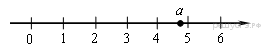
Какое из утверждений относительно этого числа является верным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
14. Задание 3 № 316336На координатной прямой отмечены числа a и b.
![]()
Какое из следующих неравенств верно?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
15. Задание 3 № 317575На координатной прямой отмечены числа a и b.
![]()
Какое из приведенных утверждений неверно?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
16. Задание 3 № 317576На координатной прямой отмечены числа a и b.
![]()
Какое из следующих утверждений является верным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
17. Задание 3 № 322417На координатной прямой отмечены числа a, b, и c.
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
18. Задание 3 № 339306На координатной прямой отмечены числа a и b.
![]()
Какое из следующих утверждений относительно этих чисел является верным?
1) a3>0 2) a − b > 0 3) ab < 1 4) a + b > 1
1. Задание 3 № 27На координатной прямой
отмечены числа ![]() и
и ![]() :
:
![]() Какое из следующих
чисел наибольшее?
Какое из следующих
чисел наибольшее?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Задание 3 № 137293Сравните числа x и y,
если ![]() ,
, ![]() .
В ответ запишите меньшее из чисел
.
В ответ запишите меньшее из чисел
3. Задание 3 № 205774О числах ![]() ,
, ![]() ,
, ![]() и
и ![]() известно,
что
известно,
что ![]() ,
, ![]() ,
, ![]() .
Сравнитe числа
.
Сравнитe числа ![]() и
и ![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) Сравнить невозможно
4) Сравнить невозможно
4. Задание 3 № 311302Известно, что ![]() .
Выберите наименьшее из чисел.
.
Выберите наименьшее из чисел.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5. Задание 3 № 311304Известно, что ![]() Выберите
наименьшее из чисел.
Выберите
наименьшее из чисел.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6. Задание 3 № 317062Числа ![]() и
и ![]() отмечены
точками на координатной прямой. Расположите в порядке возрастания
числа
отмечены
точками на координатной прямой. Расположите в порядке возрастания
числа ![]()
![]() и
1.
и
1.
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7. Задание 3 № 317132Какому из данных промежутков
принадлежит число ![]()
1) [0,5;0,6] 2) [0,6;0,7] 3) [0,7;0,8] 4) [0,8;0,9]
8. Задание 3 № 317600На координатной прямой
отмечено число ![]() Расположите
в порядке убывания числа
Расположите
в порядке убывания числа ![]()
![]() и
и ![]() В
ответе укажите номер правильного варианта.
В
ответе укажите номер правильного варианта.
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
9. Задание 3 № 322На координатной прямой отмечены числа a и x.
![]()
Какое из следующих чисел наименьшее? 1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
10. Задание 3 № 322451На координатной прямой отмечены числа a и b.
![]() Какое из следующих чисел наибольшее?
Какое из следующих чисел наибольшее?
1) a + b 2) –a 3) 2b 4) a − b
11. Задание 3 № 337301На координатной прямой отмечено число a.
![]()
Найдите наименьшее из чисел a2, a3, a4.
1) a2 2) a3 3) a4 4) не хватает данных для ответа
12. Задание 3 № 337307На координатной прямой
отмечено число ![]()
![]()
Расположите в порядке возрастания числа ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
13. Задание 3 № 337355На координатной прямой отмечено число a.
![]() Найдите наибольшее
из чисел a2, a3, a4.
Найдите наибольшее
из чисел a2, a3, a4.
1) a2 2) a3 3) a4 4) не хватает данных для ответа
14. Задание 3 № 337381Известно, что ![]() и
и ![]() —
положительные числа и
—
положительные числа и ![]() Сравните
Сравните ![]() и
и ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) сравнить невозможно
4) сравнить невозможно
15. Задание 3 № 341320На координатной прямой
точками отмечены числа ![]()
![]()
Какому числу соответствует точка B 1) ![]() 2)
2) ![]() 3) 0,42 4) 0,45
3) 0,42 4) 0,45
1. Задание 3 № 205776Какое из чисел отмечено на координатной прямой точкой A?
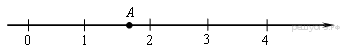 1)
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Задание 3 № 311380Одна из точек, отмеченных
на координатной прямой, соответствует числу ![]() Какая
это точка?
Какая
это точка?
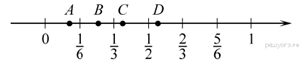 1) A
2) B 3) C 4) D
1) A
2) B 3) C 4) D
3. Задание 3 № 311392Одно из чисел ![]() отмечено на координатной прямой точкой A. Укажите это
число.
отмечено на координатной прямой точкой A. Укажите это
число.
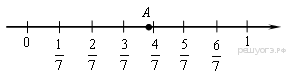 1)
1)
![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4. Задание 3 № 314146Одна из точек, отмеченных
на координатной прямой, соответствует числу ![]()
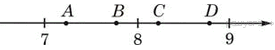 Какая это точка?
Какая это точка?
1) точка A 2) точка B 3) точка C 4) точка D
5. Задание 3 № 317074Какому из следующих чисел соответствует точка, отмеченная на координатной прямой?
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6. Задание 3 № 317102На координатной прямой точками A, B, C и D отмечены числа 0,098; −0,02; 0,09; 0,11. Какой точкой изображается число 0,09?
![]() 1) A
2) B 3) C 4) D
1) A
2) B 3) C 4) D
7. Задание 3 № 322293На координатной прямой
отмечены точки A, B, C, D. Одна из них соответствует
числу ![]() Какая
это точка?
Какая
это точка?

1) точка A 2) точка B 3) точка C 4) точка D
8. Задание 3 № 337346Известно, что
число ![]() отрицательное.
На каком из рисунков точки с координатами
отрицательное.
На каком из рисунков точки с координатами ![]() расположены
на координатной прямой в правильном порядке?
расположены
на координатной прямой в правильном порядке?
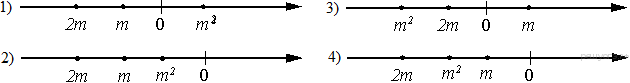
1) 1 2) 2 3) 3 4) 4
9. Задание 3 № 340578На координатной прямой отмечена точка А.
![]()
Известно, что она соответствует одному из четырех указанных
ниже чисел. Какому из чисел соответствует точка А? 1) ![]() 2)
2) ![]() 3) 0,6 4) 4
3) 0,6 4) 4
10. Задание 3 № 341На координатной прямой отмечено число a.
![]()
Какое из утверждений относительно этого числа является верным?
1) a − 8 > 0 2) 7 − a < 0 3) a − 3 > 0 4) 2 − a > 0
1. Задание 3 № 3113Известно, что ![]() Какое
из следующих чисел отрицательно?
Какое
из следующих чисел отрицательно?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Задание 3 № 3114Какое из следующих
чисел заключено между числами ![]() и
и ![]()
1) 0,1 2) 0,2 3) 0,3 4) 0,4
3. Задание 3 № 3148На координатной прямой
отмечены числа a и b. Какое из следующих
утверждений неверно? 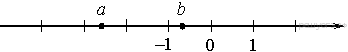
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4. Задание 3 № Какое из приведенных ниже неравенств является верным при любых значениях a и b, удовлетворяющих условию a > b?
1) b − a < −2 2) a − b > −1 3) a − b < 3 4) b − a > −3
5. Задание 3 № На координатной прямой отмечено число a.
![]()
Из следующих утверждений верное:1) (a − 6)2 > 1 2) (a − 7)2 > 1 3) a2 > 36 4) a2 > 49
6. Задание 3 № 317179На координатной прямой отмечены числа x и y. Какое из следующих утверждений об этих числах верно?
![]() 1)
1) ![]() и
и ![]() 2)
2) ![]() и
и ![]() 3)
3) ![]() и
и ![]() 4)
4) ![]() и
и ![]()
7. Задание 3 № 317223
Какому
промежутку принадлежит число ![]()
1) [4; 5] 2) [5; 6] 3) [6; 7] 4) [7; 8]
8. Задание 3 № 322419На координатной прямой отмечены числа p, q и r.
![]() Какая
из разностей p − r, p − q, r − q отрицательна?
Какая
из разностей p − r, p − q, r − q отрицательна?
1) p – r 2) p – q 3) r – q 4) ни одна из них
9. Задание 3 № 322422На координатной прямой отмечены числа a, b и c.
![]() Какая
из разностей a − b, a − c, c − b положительна?
Какая
из разностей a − b, a − c, c − b положительна?
1) a – b 2) a – c 3) c – b 4) ни одна из них
10. Задание 3 № 33748Значение какого из данных выражений положительно, если известно, что x > 0, y < 0? 1) xy 2) (x − y)y 3) (y − x)y 4) (y − x)x
|
||||||||||||||||||||||||||||||||||||||||
|
На координатной прямой отмечены точки A, B, C, и D.
На координатной прямой отмечены точки A, B, C, и D.
Одна из них соответствует числу 13217. Какая это точка?
На
координатной прямой отмечены точки
Одна
из них соответствует числу
На координатной прямой отмечены точки A, B, C, и D.
Одна из них соответствует числу 8011. Какая это точка?
|
|||||||||||||||||||||||||||||||||||||||
Задание 4
1. Задание 4 № 137272Найдите значение выражения 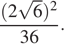
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) 4
4) 4
2. Задание 4 № 137281Вычислите: ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3. Задание 4 № 137285 Найдите значение выражения ![]() .
.
4. Задание 4 № 317389 Найдите значение выражения ![]()
1) 5 2) ![]() 3)
3) ![]() 4) 40
4) 40
5. Задание 4 № 318630Чему равно значение
выражения ![]()
1) 6 2) 12 3) 18 4) 36
6. Задание 4 № 337339Найдите значение выражения ![]()
1) 198 2) ![]() 3) 3564 4) 2178
3) 3564 4) 2178
7. Задание 4 № 337462Найдите значение выражения ![]()
1) 360 2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Задание 4 № 337692Найдите значение выражения (1,7 · 10− 5)(2 · 10− 2).
1) 0,0000034 2) 34000000000 3) 0,000000034 4) 0,00000034
9. Задание 4 № 337700Найдите значение выражения ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) 90
4) 90
10. Задание 4 № 33778Найдите значение
выражения ![]()
1) ![]() 2) 22 3)
2) 22 3) ![]() 4)
4) ![]()
11. Задание 4 № 34119Найдите значение выражения ![]()
1) 2600000 2) 0,000026 3) 0,0000026 4) 0,00026
12. Задание 4 № 34989Найдите значение
выражения ![]()
1)![]() 2)
2)![]() 3)
3)![]() 4)
4)![]()
13. Задание 4 № 35296Какое из данных ниже
чисел является значением выражения 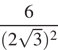 ?
?
1)![]() 2)
2)![]() 3)
3)![]() 4)
4)![]()
14. Задание 4 № 35338Найдите значение
выражения ![]()
15. Задание 4 № 35540Какое из данных ниже
чисел является значением выражения ![]() 1) 16 2)
1) 16 2) ![]() 3) −16 4)
3) −16 4) ![]()
1. Задание 4 № 28 Значение какого из выражений является числом рациональным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Задание 4 № 137268 Расположите в порядке
возрастания числа: ![]() ;
; ![]() ;
5,5.
;
5,5.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3. Задание 4 № 137269 Расположите в порядке убывания
числа: ![]() ;
; ![]() ;
5,5.
;
5,5.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4. Задание 4 № 287934 Расположите в порядке
возрастания: ![]()
![]()
![]()
|
1) |
2) |
|
3) |
4) |
5. Задание 4 № 287943 Расположите в порядке возрастания:
![]()
![]()
![]()
|
1) |
2) |
|
3) |
4) |
6. Задание 4 № 287944 Расположите в порядке
убывания: ![]()
![]()
![]()
|
1) |
2) |
|
3) |
4) |
7. Задание 4 № 311750Укажите наибольшее из следующих чисел:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Задание 4 № 314246 Сравните числа ![]() и
16.
и
16.
1) ![]() 2)
2) ![]() 3)
3) ![]()
9. Задание 4 № 314250 Какое из чисел больше: ![]() или
или ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]()
10. Задание 4 № 31436Значение какого из данных выражений является наименьшим?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
11. Задание 4 № 314377 В каком случае
числа ![]() и
6 расположены в порядке возрастания?
и
6 расположены в порядке возрастания?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
12. Задание 4 № 314448 Сравните числа ![]() и
12.
и
12.
1) ![]() 2)
2) ![]() 3)
3) ![]()
13. Задание 4 № 31445Какое из чисел больше: ![]() или
или ![]() ?
?
1) ![]() 2)
2) ![]() 3)
3) ![]()
14. Задание 4 № 31655Значение какого из выражений является числом иррациональным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
15. Задание 4 № 31660Расстояние от Юпитера — одной из планет Солнечной системы — до Солнца равно 778,1 млн км. Как эта величина записывается в стандартном виде?
1) 7,781·1011 2) 7,781·108 3) 7,781·1010 4) 7,781·109
16. Задание 4 № 31662На рулоне обоев имеется надпись, гарантирующая, что длина полотна обоев находится в пределах 10 ± 0,05 м. Какую длину не может иметь полотно при этом условии?
1) 10,23 2) 10,05 3) 9,96 4) 10,03
17. Задание 4 № 31729Какое из чисел ![]()
![]()
![]() является
иррациональным?
является
иррациональным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) ни одно из этих чисел
4) ни одно из этих чисел
18. Задание 4 № 31730Какое из чисел ![]()
![]()
![]() является
рациональным?
является
рациональным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) Все эти числа иррациональны.
4) Все эти числа иррациональны.
19. Задание 4 № 317368 Значение какого из чисел является наибольшим?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) 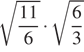
20. Задание 4 № 317586 Какое из следующих чисел является наименьшим?
1) 1,7·10−3 2) 2,3·10−4 3) 4,5·10−3 4) 8,9·10−4
21. Задание 4 № 317587 Какое из следующих чисел является наибольшим?
1) 1,8·10−3 2) 4,7·10−4 3) 2,9·10−5 4) 9,5·10 −3
22. Задание 4 № 317728 Масса Луны равна 7,35·1022 кг. Выразите массу Луны в млн тонн.
1) 7,35⋅1010 млн т 2) 7,35⋅1013 млн т 3) 7,35⋅1016 млн т 4) 7,35⋅1019 млн т
23. Задание 4 № 317741Численность населения Китая составляет 1,3·109 человек, а Вьетнама — 8,5·107 человек. Во сколько раз численность населения Китая больше численности населения Вьетнама?
1) примерно в 6,5 раз 2) примерно в 15 раз 3) примерно в 150 раз 4) примерно в 1,5 раза
24. Задание 4 № 317753 Расстояние от Земли до Солнца равно 147,1 млн км. В каком случае записана эта же величина?
1) 1,471⋅1010 км 2) 1,471⋅108 км 3) 1,471⋅107 км 4) 1,471⋅106 км
25. Задание 4 № 318729 Значение какого выражения
является рациональным числом? 1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
26. Задание 4 № 318753 Значение какого из данных выражений является наименьшим?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
27. Задание 4 № 337271 Найдите значение выражения ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
28. Задание 4 № 337291 В лабораторию купили
электронный микроскоп, который даёт возможность различать объекты размером
до ![]() Выразите
эту величину в миллиметрах.
Выразите
эту величину в миллиметрах.
1) 0,002 2) 0,0002 3) 0,00002 4) 0,000002
29. Задание 4 № 337311 Между какими числами
заключено число ![]()
1) 8 и 9 2) 72 и 74 3) 24 и 26 4) 4 и 5
30. Задание 4 № 337389 Какое из данных чисел принадлежит промежутку [6; 7]?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
31. Задание 4 № 342023 Значение какого из выражений является числом иррациональным?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
32. Задание 4 № 348601 Площадь территории
России составляет ![]() км
км![]() ,
а Нигерии -
,
а Нигерии - ![]() км
км![]() .
Во сколько раз площадь территории России больше площади территории Нигерии?
.
Во сколько раз площадь территории России больше площади территории Нигерии?
1) примерно в 18 раз 2) примерно в 180 раз 3) примерно в 1,8 раза 4) примерно в 5,4 раза
33. Задание 4 № 348955 Площадь территории России составляет 1,7 · 107 км2, а Великобритании — 2,6⋅105 км2. Во сколько раз площадь территории России больше площади территории Великобритании?
1) примерно в 65 раз 2) примерно в 650 раз 3) примерно в 6,5 раза 4) примерно в 1,5 раза
34. Задание 4 № 351591В лабораторию купили
электронный микроскоп, который даёт возможность различать объекты размером
до ![]() Выразите
эту величину в миллиметрах.
Выразите
эту величину в миллиметрах.
1) 0,0000027 2) 0,000027 3) 0,00027 4) 0,027
1. Задание 4 № 137275 Какое из следующих
выражений равно ![]() ?
?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Задание 4 № 137276 Какое из следующих
выражений равно ![]() ?
?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3. Задание 4 № 137278 Представьте
выражение ![]() в
виде степени с основанием c.
в
виде степени с основанием c.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4. Задание 4 № 137279 Представьте
выражение ![]() в
виде степени с основанием x.
в
виде степени с основанием x.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5. Задание 4 № 137280 Найдите значение выражения ![]() при
при ![]() .
.
1) −125 2) 125 3) ![]() 4)
4) ![]()
6. Задание 4 № 137292 Сравните числа x и y,
если ![]() ,
, ![]() .
В ответ запишите большее число.
.
В ответ запишите большее число.
7. Задание 4 № 318723 Какому из следующих
выражений равна дробь ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Задание 4 № 338098 Представьте выражение ![]() в
виде степени с основанием
в
виде степени с основанием ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
9. Задание 4 № 338113 Представьте выражение ![]() в
виде степени с основанием
в
виде степени с основанием ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
10. Задание 4 № 341212 Представьте выражение ![]() в
виде степени с основанием x.
в
виде степени с основанием x.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
11. Задание 4 № 348386 Какое из данных
чисел ![]() является
иррациональным? 1)
является
иррациональным? 1) ![]() 2)
2) ![]() 3)
3) ![]() 4) все эти числа рациональны
4) все эти числа рациональны
|
12. Задание 4 № 348417 Какое из данных ниже
чисел является значением выражения |
2) |
3) |
4) 38 |
13. Задание 4 № 348572 Какое из данных ниже чисел
является значением выражения ![]() 1)
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
14. Задание 4 № 348654 Какое из данных ниже
выражений при любых значениях ![]() равно
дроби
равно
дроби ![]() ?
1)
?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
ЗАДАНИЕ 5
1. Задание 5 № 315131 В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
|
Вещество |
Дети от 1 года до 14 лет |
Мужчины |
Женщины |
|
Жиры |
40—97 |
70—154 |
60—102 |
|
Белки |
36—87 |
65—117 |
58—87 |
|
Углеводы |
170—420 |
257—586 |
|
Какой вывод о суточном потреблении жиров, белков и углеводов 7-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 42 г жиров, 35 г белков и 190 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме. 2) Потребление белков в норме.
3) Потребление углеводов в норме.
. Задание 5 № 206196 В ходе химической реакции количество исходного вещества (реагента), которое еще не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат — масса оставшегося реагента, который еще не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты?
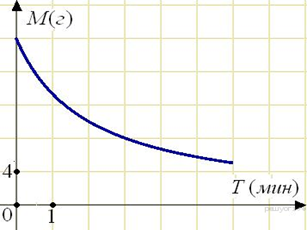
2. Задание 5 № 206197 Мощность отопителя в автомобиле регулируется дополнительным сопротивлением, которое можно менять, поворачивая рукоятку в салоне машины. При этом меняется сила тока в электрической цепи электродвигателя – чем меньше сопротивление, тем больше сила тока и тем быстрее вращается мотор отопителя. На рисунке показана зависимость силы тока от величины сопротивления. На оси абсцисс откладывается сопротивление (в Омах), на оси ординат — сила тока в Амперах. Ток в цепи электродвигателя уменьшился с 8 до 6 Ампер. На сколько Омов при этом увеличилось сопротивление цепи?
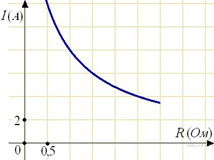
3. Задание 5 № 311298
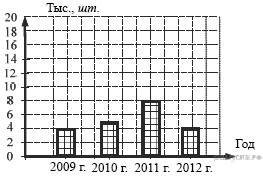 На диаграмме показано количество
посаженных деревьев и кустарников в г. Сочи за период с 2009 по 2012 гг.
Определите, сколько всего было посажено зелёных насаждений за 2011 г. и
2012 г.?
На диаграмме показано количество
посаженных деревьев и кустарников в г. Сочи за период с 2009 по 2012 гг.
Определите, сколько всего было посажено зелёных насаждений за 2011 г. и
2012 г.?
1) 10 000 2) 4 000 3) 12 000 4) 8 000
4. Задание 5 № 311484 На рисунке показано, как изменялась температура воздуха на протяжении
одних суток. По горизонтали указано время суток, по вертикали — значение
температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим
значением температуры в первой половине этих суток. Ответ дайте в градусах
Цельсия.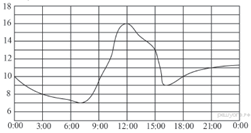
5. Задание 5 № 311515
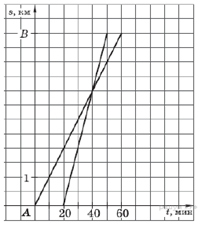 Из пункта
Из пункта ![]() в пункт
в пункт ![]() вышел пешеход, и через некоторое время вслед за ним выехал велосипедист. На
рисунке изображены графики движения пешехода и велосипедиста. На
сколько километров в час скорость пешехода меньше скорости
велосипедиста?
вышел пешеход, и через некоторое время вслед за ним выехал велосипедист. На
рисунке изображены графики движения пешехода и велосипедиста. На
сколько километров в час скорость пешехода меньше скорости
велосипедиста?
6. Задание 5 № 311518
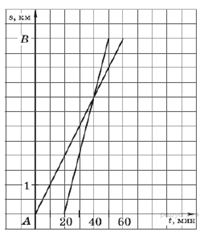 Из пункта A в
пункт B вышел пешеход, и через некоторое время вслед за ним
выехал велосипедист. На рисунке изображены графики движения пешехода и
велосипедиста. На сколько минут меньше затратил на путь из A в Bвелосипедист,
чем пешеход?
Из пункта A в
пункт B вышел пешеход, и через некоторое время вслед за ним
выехал велосипедист. На рисунке изображены графики движения пешехода и
велосипедиста. На сколько минут меньше затратил на путь из A в Bвелосипедист,
чем пешеход?
7. Задание 5 № 311521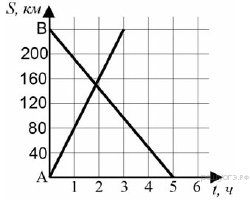 На рисунке изображен график движения автомобиля
из пункта
На рисунке изображен график движения автомобиля
из пункта ![]() в пункт
в пункт ![]() и автобуса из пункта
и автобуса из пункта ![]() в пункт
в пункт ![]() . На сколько километров в час скорость автомобиля
больше скорости автобуса?
. На сколько километров в час скорость автомобиля
больше скорости автобуса?
8. Задание 5 № 311960 На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
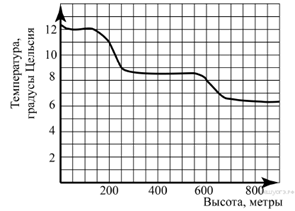
Определите по графику, на сколько градусов температура на высоте 200 метров выше, чем на высоте 650 метров.
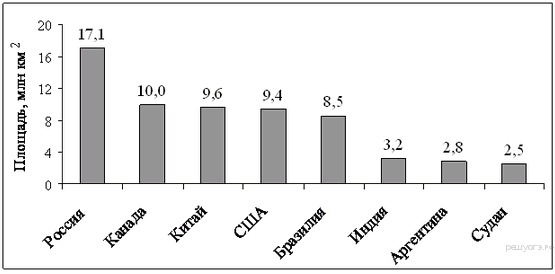
9. Задание 5 № 315197На диаграмме представлены некоторые из крупнейших по площади территории стран мира. Во сколько примерно раз площадь США больше площади Судана? (Ответ округлите до целых.)
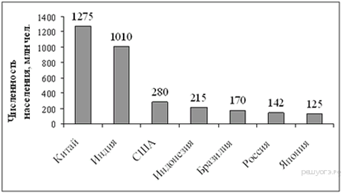
10. Задание 5 № 315200На диаграмме представлены некоторые из крупнейших по численности населения стран мира. Численность населения какого государства примерно в 6 раз меньше численности населения Китая? В ответе напишите численность населения этого государства в млн чел.
11. Задание 5 № 316350На графике показано, сколько человек зарегистрировалось с 13 января по 4 марта 2013 года в качестве участников конференции. По горизонтали указаны числа месяцев, а по вертикали — количество человек.
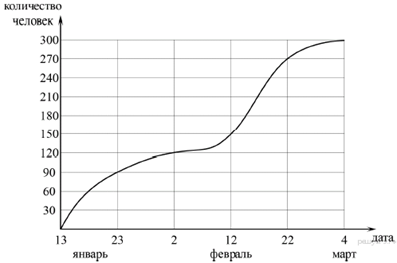
Во сколько раз возросло количество зарегистрировавшихся с 23 января по 22 февраля?
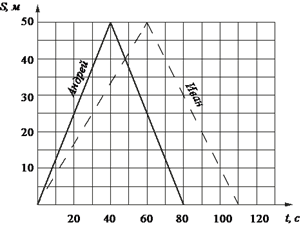
12. Задание 5 № 322036 Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время, а по вертикальной — расстояние пловца от старта. Кто выиграл соревнование? В ответе запишите, на сколько секунд он обогнал соперника.
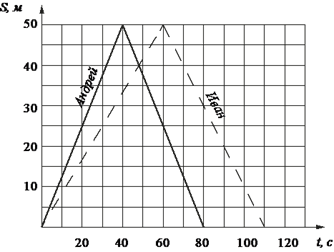
13. Задание 5 № 322037 Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время, а по вертикальной – расстояние пловца от старта. Кто быстрее проплыл первую половину дистанции? В ответе запишите, на сколько секунд быстрее он проплыл первую половину дистанции.
14. Задание 5 № 322165
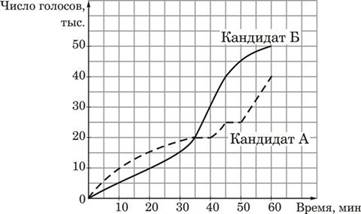 На графиках показано, как во время телевизионных
дебатов между кандидатами А и Б телезрители голосовали за каждого
из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?
На графиках показано, как во время телевизионных
дебатов между кандидатами А и Б телезрители голосовали за каждого
из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?
15. Задание 5 № 322173
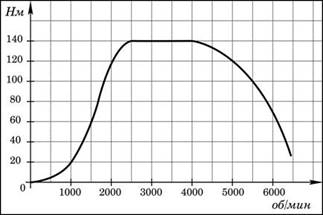 На графике изображена зависимость
крутящего момента двигателя от числа его оборотов в минуту. На оси
абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий
момент в Н·м. На сколько Н·м увеличился крутящий момент, если
число оборотов двигателя возросло с 1000 до 1500 оборотов в минуту?
На графике изображена зависимость
крутящего момента двигателя от числа его оборотов в минуту. На оси
абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий
момент в Н·м. На сколько Н·м увеличился крутящий момент, если
число оборотов двигателя возросло с 1000 до 1500 оборотов в минуту?
16. Задание 5 № 322186 При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, на сколько вольт упадет напряжение за 2 часа с начала работы фонарика.

17. Задание 5 № 322188 При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, на сколько вольт упадет напряжение c 6-го по 30-й час работы фонарика.

18. Задание 5 № 322193
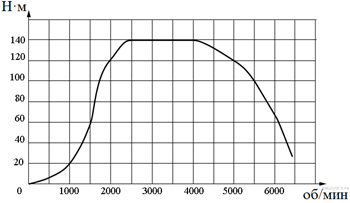
На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н⋅м. На сколько оборотов в минуту должно ускориться вращение, чтобы крутящий момент вырос с 20 Н⋅м до 120 Н⋅м?
19. Задание 5 № 340985 На
рисунке показано, как изменялась температура воздуха на протяжении
одних суток. По горизонтали указано время суток, по вертикали — значение
температуры в градусах Цельсия. Найдите разность между наименьшим и
наибольшим значениями температуры. Ответ дайте в градусах Цельсия.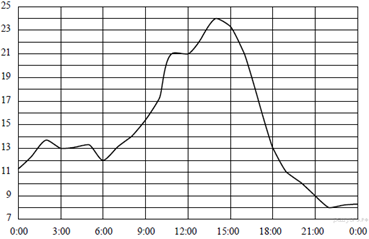
20. Задание 5 № 341360 На
рисунке показан график разряда батарейки в карманном фонарике. На
горизонтальной оси отмечается время работы фонарика в часах, на
вертикальной оси — напряжение в вольтах. Определите по рисунку, какое
напряжение будет давать батарейка через 5 часов работы фонарика. Ответ
дайте в вольтах.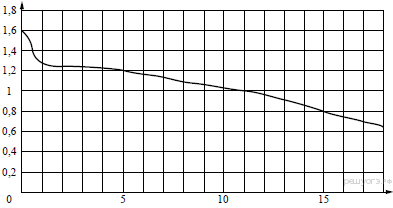
1. Задание 5 № 42 На
графике изображена зависимость атмосферного давления (в миллиметрах
ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте
(в км) летит воздушный шар, если барометр, находящийся в корзине шара,
показывает давление 540 миллиметров ртутного столба?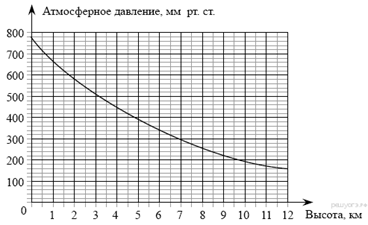
2. Задание 5 № 206194 Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч?
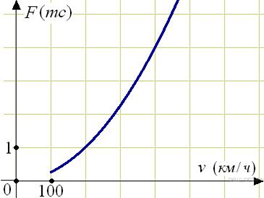
3. Задание 5 № 206195 В аэропорту чемоданы пассажиров поднимают в зал выдачи багажа по транспортерной ленте. При проектировании транспортера необходимо учитывать допустимую силу натяжения ленты транспортера. На рисунке изображена зависимость натяжения ленты от угла наклона транспортера к горизонту при расчетной нагрузке. На оси абсцисс откладывается угол подъема в градусах, на оси ординат – сила натяжения транспортерной ленты (в килограммах силы). При каком угле наклона сила натяжения достигает 150 кгс? Ответ дайте в градусах.
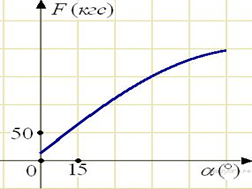
4. Задание 5 № 311322
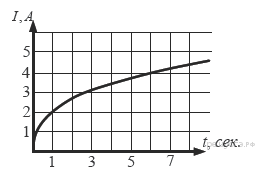 На
рисунке изображен график изменения силы тока при подключении цепи, содержащей
реостат, к источнику тока. По вертикальной оси откладывается сила
тока (в A), по горизонтальной — время (в сек). По рисунку
определите силу тока через 6 секунд с момента подключения данной цепи.
На
рисунке изображен график изменения силы тока при подключении цепи, содержащей
реостат, к источнику тока. По вертикальной оси откладывается сила
тока (в A), по горизонтальной — время (в сек). По рисунку
определите силу тока через 6 секунд с момента подключения данной цепи.
5. Задание 5 № 311334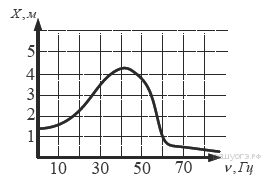 На
рисунке изображен график зависимости амплитуды вынужденных колебаний
от частоты колебаний. По вертикальной оси откладывается амплитуда (в м),
по горизонтальной — частота колебаний (в Гц). По рисунку определите частоту
колебаний, если амплитуда была равна 1 м.
На
рисунке изображен график зависимости амплитуды вынужденных колебаний
от частоты колебаний. По вертикальной оси откладывается амплитуда (в м),
по горизонтальной — частота колебаний (в Гц). По рисунку определите частоту
колебаний, если амплитуда была равна 1 м.
6. Задание 5 № 311357
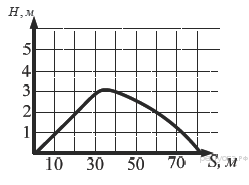 На рисунке изображен график полета тела, брошенного
под углом к горизонту. По вертикальной оси откладывается расстояние от
земли (в м), по горизонтальной оси — пройденный путь (в м). По рисунку
определите, на какой высоте будет находиться тело в момент времени, когда
оно пролетит 60 метров.
На рисунке изображен график полета тела, брошенного
под углом к горизонту. По вертикальной оси откладывается расстояние от
земли (в м), по горизонтальной оси — пройденный путь (в м). По рисунку
определите, на какой высоте будет находиться тело в момент времени, когда
оно пролетит 60 метров.
7. Задание 5 № 311389 На
графике показан процесс разогрева двигателя легкового автомобиля. На оси
абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на
оси ординат — температура двигателя в градусах Цельсия. Определите
по графику, сколько минут двигатель нагревался до температуры 50 °C с момента
запуска двигателя.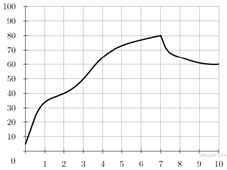
8. Задание 5 № 311477На графике изображена зависимость атмосферного давления
(в миллиметрах ртутного столба) от высоты над уровнем моря (в
километрах).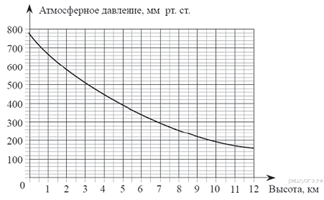 На
сколько миллиметров ртутного столбы отличается давление на высоте 2 км
от давления на высоте 8 км?
На
сколько миллиметров ртутного столбы отличается давление на высоте 2 км
от давления на высоте 8 км?
9. Задание 5 № 311481 На
графике представлена динамика изменения курса доллара США в рублях за период
с 19 ноября по 19 декабря. По горизонтальной оси отложены даты, по
вертикальной — значения доллара США. Шаг по вертикальной оси равен
0,0372 руб. Определите по графику, каким был курс доллара США к рублю 21
ноября.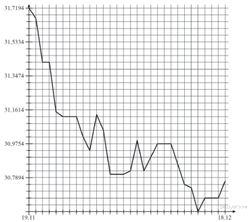
10. Задание 5 № 311764 На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наибольшее значение температуры. Ответ дайте в градусах Цельсия.
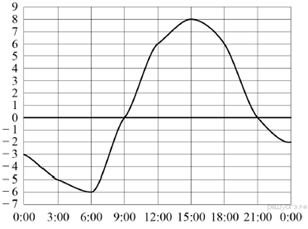
11. Задание 5 № 311852 На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наименьшее значение температуры. Ответ дайте в градусах Цельсия.
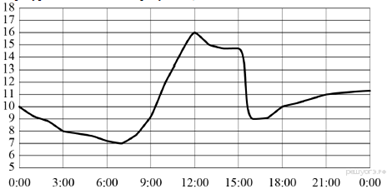
12. Задание 5 № 314672 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Большого Шелома?
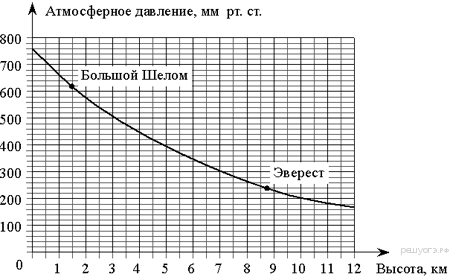
13. Задание 5 № 314689На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.
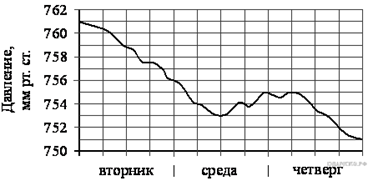
14. Задание 5 № 314788 Компания предлагает на выбор два разных тарифа для оплаты телефонных разговоров: тариф А и тариф В. Для каждого тарифа зависимость стоимости разговора от его продолжительности изображена графически. На сколько минут хватит 550 р., если используется тариф В?
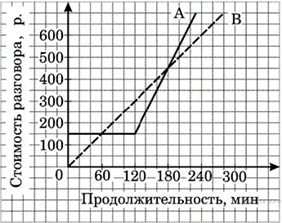
15. Задание 5 № 322032 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) во вторник в 12 часов дня.
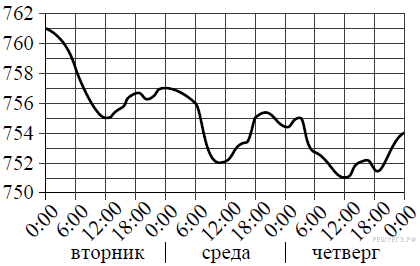
16. Задание 5 № 322042 При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость (в км/ч), по вертикальной – тормозной путь (в метрах). Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 70 км/ч. Ответ дайте в метрах.
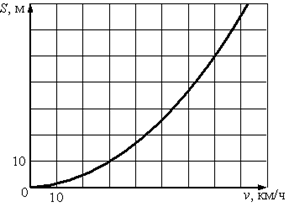
17. Задание 5 № 322045 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Определите по графику, на какой высоте атмосферное давление равно 660 мм рт. ст. Ответ дайте в километрах.
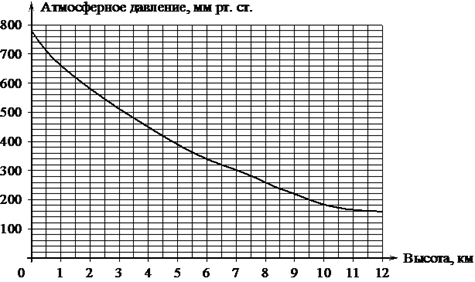
18. Задание 5 № 322046На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 6 км. Ответ дайте в миллиметрах ртутного столба.
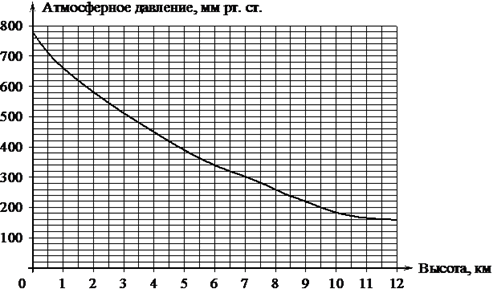
19. Задание 5 № 322092
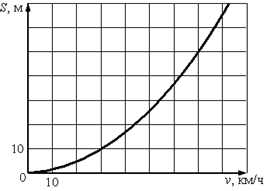 При резком торможении расстояние,
пройденное автомобилем до полной остановки (тормозной путь), зависит
от скорости, с которой автомобиль двигался. На рисунке показан график
этой зависимости (для сухой асфальтовой дороги). По горизонтальной
оси откладывается скорость (в км/ч), по вертикальной – тормозной
путь (в метрах). Определите по графику, с какой скоростью двигался автомобиль,
если его тормозной путь составил 50 метров. Ответ дайте в километрах в
час.
При резком торможении расстояние,
пройденное автомобилем до полной остановки (тормозной путь), зависит
от скорости, с которой автомобиль двигался. На рисунке показан график
этой зависимости (для сухой асфальтовой дороги). По горизонтальной
оси откладывается скорость (в км/ч), по вертикальной – тормозной
путь (в метрах). Определите по графику, с какой скоростью двигался автомобиль,
если его тормозной путь составил 50 метров. Ответ дайте в километрах в
час.
20. Задание 5 № 322099 На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наибольшее значение температуры. Ответ дайте в градусах Цельсия.

21. Задание 5 № 322104На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наименьшее значение температуры. Ответ дайте в градусах Цельсия.

22. Задание 5 № 322139 На рисунке показано, как изменялась температура на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Сколько часов во второй половине дня температура превышала 10 °C?
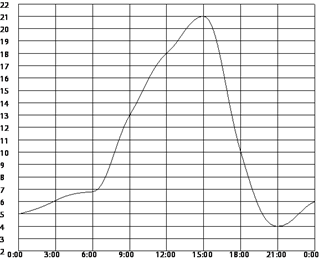
23. Задание 5 № 322141На рисунке показано, как изменялась температура на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Сколько часов в первой половине дня температура превышала 25 °C?

24. Задание 5 № 322154 На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Сколько часов в первой половине дня температура не превышала 0° C?
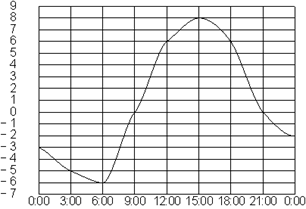
25. Задание 5 № 339223 На рисунке показано, как изменялась температура на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Сколько часов после 12:00 температура превышала 29°C?
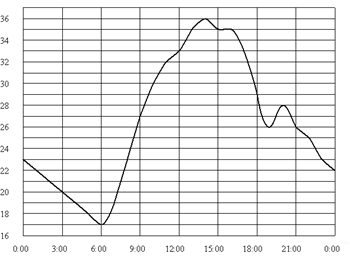
26. Задание 5 № 348385 На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 40 °C до 90 °C.
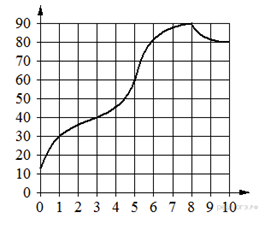
ЗАДАНИЕ 6
1. Задание 6 № 85 Найдите
корни уравнения ![]() .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
2. Задание 6 № 311469 Решите
уравнение ![]() .
.
3. Задание 6 № 338480 Решите
уравнение ![]()
4. Задание 6 № 338488 Решите уравнение ![]()
5. Задание 6 № 338495 Решите
уравнение ![]()
6. Задание 6 № 338500 При
каком значении ![]() значения выражений
значения выражений ![]() и
и ![]() равны?
равны?
7. Задание 6 № 338509 Решите
уравнение ![]()
8. Задание 6 № 338527 Решите
уравнение ![]()
9. Задание 6 № 338557 Решите
уравнение ![]()
10. Задание 6 № 338560 Решите
уравнение ![]()
11. Задание 6 № 338606 Решите
уравнение ![]()
12. Задание 6 № 338610 Решите
уравнение ![]()
13. Задание 6 № 338658 Решите
уравнение ![]()
14. Задание 6 № 338868 Решите
уравнение ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
15. Задание 6 № 341216 Решите
уравнение ![]()
16. Задание 6 № 353480 Найдите
корень уравнения ![]()
1. Задание 6 № 137381 Решите
уравнение ![]() .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
2. Задание 6 № 137382 Решите уравнение ![]() .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
3. Задание 6 № 137383 Решите
уравнение ![]() .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
4. Задание 6 № 311405 Найдите корни уравнения ![]() .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
5. Задание 6 № 311446 Найдите
корни уравнения ![]() .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
6. Задание 6 № 311689 Найдите корни уравнения ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7. Задание 6 № 314495 Найдите корни уравнения ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
8. Задание 6 № 320540
 Две прямые пересекаются в
точке C (см. рис.). Найдите абсциссу точки C.
Две прямые пересекаются в
точке C (см. рис.). Найдите абсциссу точки C.
9. Задание 6 № 320541
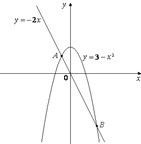 На рисунке изображены графики функций
На рисунке изображены графики функций ![]() и
и ![]() Вычислите
координаты точки B.
Вычислите
координаты точки B.
Запишите координаты в ответ без пробелов и знаков препинания.
10. Задание 6 № 338180 Уравнение ![]() имеет корни −6; 4. Найдите
имеет корни −6; 4. Найдите ![]()
11. Задание 6 № 338202 Квадратный
трёхчлен разложен на множители: ![]() Найдите
Найдите ![]()
12. Задание 6 № 338494 Решите
уравнение ![]()
13. Задание 6 № 338518 Решите
уравнение ![]()
14. Задание 6 № 338526 Решите
уравнение ![]()
15. Задание 6 № 338915 Решите
уравнение ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
16. Задание 6 № 353508 Уравнение ![]() имеет корни −5; 7. Найдите
имеет корни −5; 7. Найдите ![]()
1. Задание 6 № 311381Решите уравнение: ![]() .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
2. Задание 6 № 311755 Решите уравнение ![]()
3. Задание 6 № 316225 Решите
уравнение: ![]()
4. Задание 6 № 316341 Решите уравнение: ![]()
5. Задание 6 № 338483 Решите уравнение ![]()
6. Задание 6 № 338503 Решите
уравнение ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7. Задание 6 № 338583 Решите
уравнение ![]()
8. Задание 6 № 338723 Решите
уравнение ![]()
9. Задание 6 № 338805 Решите уравнение ![]()
10. Задание 6 № 338937 Решите уравнение ![]()
11. Задание 6 № 341402 Решите уравнение ![]()
1. Задание 6 № 311315 Решите систему уравнений 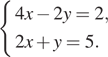
В ответе запишите сумму решений системы.
2. Задание 6 № 311327 Решите
систему уравнений 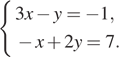
В ответе запишите сумму решений системы.
3. Задание 6 № 311338 Решите систему уравнений 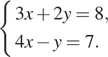
В ответе запишите сумму решений системы.
4. Задание 6 № 311350 Решите систему уравнений ![]()
В ответе запишите сумму решений системы.
5. Задание 6 № 311360 Решите систему уравнений ![]()
В ответе запишите сумму решений системы.
6. Задание 6 № 311370 Решите систему уравнений ![]()
В ответе запишите сумму решений системы.
1. Задание 6 № 314489 Найдите наибольшее значение x, удовлетворяющее системе
неравенств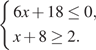
2. Задание 6 № 314543 Найдите
наибольшее значение ![]() , удовлетворяющее системе неравенств
, удовлетворяющее системе неравенств 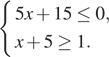
ЗАДАНИЕ 7
1. Задание 7 № 137249 На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?
2. Задание 7 № 137250 Число хвойных деревьев в парке относится к числу лиственных как 1:4. Сколько процентов деревьев в парке составляют лиственные?
3. Задание 7 № 137253 Тест по математике содержит 30 заданий, из которых 18 заданий по алгебре, остальные –– по геометрии. В каком отношении содержатся в тесте алгебраические и геометрические задания?
|
1) 3:2 |
2) 2:3 |
3) 3:5 |
4) 5:3 |
4. Задание 7 № 314122 Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 24 га и распределена между зерновыми и овощными культурами в отношении 5:3. Сколько гектаров занимают овощные культуры?
5. Задание 7 № 317836 Во время выборов голоса избирателей между двумя кандидатами распределились в отношении 3:2. Сколько процентов голосов получил проигравший?
6. Задание 7 № 317937 Для приготовления фарша взяли говядину и свинину в отношении 7:13. Какой процент в фарше составляет свинина?
7. Задание 7 № 317938 Для фруктового напитка смешивают яблочный и виноградный сок в отношении 13:7. Какой процент в этом напитке составляет виноградный сок?
8. Задание 7 № 317939 Для приготовления чайной смеси смешивают индийский и цейлонский чай в отношении 9:11. Какой процент в этой смеси составляет цейлонский чай?
1. Задание 7 № 43 Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?
2. Задание 7 № 69 Чашка, которая стоила 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?
3. Задание 7 № 137243 Городской бюджет составляет 45 млн. р., а расходы на одну из его статей составили 12,5%. Сколько рублей потрачено на эту статью бюджета?
4. Задание 7 № 137245 Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
5. Задание 7 № 137246 Товар на распродаже уценили на 20%, при этом он стал стоить 680 р. Сколько стоил товар до распродажи?
6. Задание 7 № 137247 Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма в рублях из этой прибыли должна пойти на выплату частным акционерам?
7. Задание 7 № 137248 Акции предприятия распределены между государством и частными лицами в отношении 3:5. Общая прибыль предприятия после уплаты налогов за год составила 32 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
Ответ укажите в рублях.
8. Задание 7 № 137251 Средний вес мальчиков того же возраста, что и Сергей, равен 48 кг. Вес Сергея составляет 120% среднего веса. Сколько весит Сергей?
9. Задание 7 № 137252 В начале года число абонентов телефонной компании «Север» составляло 200 тыс. чел., а в конце года их стало 210 тыс. чел. На сколько процентов увеличилось за год число абонентов этой компании?
10. Задание 7 № 137257 На счет в банке, доход по которому составляет 15% годовых, внесли 24 тыс. р. Сколько тысяч рублей будет на этом счете через год, если никаких операций со счетом проводиться не будет?
11. Задание 7 № 137258 Какая сумма (в рублях) будет проставлена в кассовом чеке, если стоимость товара 520 р., и покупатель оплачивает его по дисконтной карте с 5%-ной скидкой?
12. Задание 7 № 137264 В понедельник некоторый товар поступил в продажу по цене 1000 р. В соответствии с принятыми в магазине правилами цена товара в течение недели остается неизменной, а в первый день каждой следующей недели снижается на 20% от предыдущей цены. Сколько рублей будет стоить товар на двенадцатый день после поступления в продажу?
13. Задание 7 № 311614 Брюки дороже рубашки на 20%, а пиджак дороже рубашки на 44%. На сколько процентов пиджак дороже брюк?
14. Задание 7 № 311853 Виноград стоит 160 рублей за килограмм, а малина — 200 рублей за килограмм. На сколько процентов виноград дешевле малины?
15. Задание 7 № 314120 Кисть, которая стоила 240 рублей, продаётся с 25%-й скидкой. При покупке двух таких кистей покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?
16. Задание 7 № 314125 Спортивный магазин проводит акцию: «Любая футболка по цене 300 рублей. При покупке двух футболок — скидка на вторую 60%». Сколько рублей придётся заплатить за покупку двух футболок?
17. Задание 7 № 314405 В течение августа помидоры подешевели на 50%, а затем в течение сентября подорожали на 70%. Какая цена меньше: в начале августа или в конце сентября — и на сколько процентов. В ответе укажите количество процентов.
18. Задание 7 № 316325 Поступивший в продажу в апреле мобильный телефон стоил 4000 рублей. В сентябре он стал стоить 2560 рублей. На сколько процентов снизилась цена на мобильный телефон в период с апреля по сентябрь?
19. Задание 7 № 317816 Туристическая фирма организует трехдневные автобусные экскурсии. Стоимость экскурсии для одного человека составляет 3500 р. Группам предоставляются скидки: группе от 3 до 10 человек — 5%, группе более 10 человек — 10%. Сколько заплатит за экскурсию группа из 8 человек?
20. Задание 7 № 317842 Расходы на одну из статей городского бюджета составляют 12,5%. Выразите эту часть бюджета десятичной дробью.
21. Задание 7 № 317843 Содержание некоторого вещества в таблетке витамина составляет 2,5%. Выразите эту часть десятичной дробью.
22. Задание 7 № 317887 Плата за телефон составляет 340 рублей в месяц. В следующем году она увеличится на 2%. Сколько придётся платить ежемесячно за телефон в следующем году?
23. Задание 7 № 317936
В период распродажи магазин снижал цены дважды: в первый раз на 30%, во второй — на 45%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1400 р.?
24. Задание 7 № 317941 На предприятии работало 240 сотрудников. После модернизации производства их число сократилось до 192. На сколько процентов сократилось число сотрудников предприятия?
25. Задание 7 № 317942 В начале 2010 г. в поселке было 730 жителей, а в начале 2011 г. их стало 803. На сколько процентов увеличилось число жителей поселка за год?
26. Задание 7 № 317951 После уценки телевизора его новая цена составила 0,52 старой. На сколько процентов уменьшилась цена телевизора в результате уценки?
27. Задание 7 № 317971 Число дорожно-транспортных происшествий в летний период составило 0,71 их числа в зимний период. На сколько процентов уменьшилось число дорожно-транспортных происшествий летом по сравнению с зимой?
28. Задание 7 № 318031 В начале учебного года в школе было 1250 учащихся, а к концу года их стало 950. На сколько процентов уменьшилось за год число учащихся?
29. Задание 7 № 318186 Клубника стоит 180 рублей за килограмм, а виноград – 160 рублей за килограмм. На сколько процентов клубника дороже винограда?
30. Задание 7 № 318225 Магазин делает пенсионерам скидку на определённое количество процентов от стоимости покупки. Десяток яиц стоит в магазине 35 рублей, а пенсионер заплатил за них 33 рубля 25 копеек. Сколько процентов составляет скидка для пенсионера?
31. Задание 7 № 318293 Магазин детских товаров закупает погремушку по оптовой цене 260 рублей за одну штуку и продаёт с 40-процентной наценкой. Сколько будут стоить 3 такие погремушки, купленные в этом магазине?
32. Задание 7 № 318314 Суточная норма потребления витамина С для взрослого человека составляет 60 мг. Один помидор в среднем содержит 17 мг витамина С. Сколько процентов суточной нормы витамина С получил человек, съевший один помидор? Ответ округлите до целых.
33. Задание 7 № 318325 В городе 190 000 жителей, причем 29% – это пенсионеры. Сколько примерно человек составляет эта категория жителей? Ответ округлите до тысяч.
1. Задание 7 № 137244 Перед
представлением в цирк для продажи было заготовлено некоторое количество
шариков. Перед началом представления было продано ![]() всех воздушных шариков, а в антракте – еще 12
штук. После этого осталась половина всех шариков. Сколько шариков было
первоначально?
всех воздушных шариков, а в антракте – еще 12
штук. После этого осталась половина всех шариков. Сколько шариков было
первоначально?
2. Задание 7 № 311917 На
многопредметной олимпиаде ![]() всех участников получили дипломы,
всех участников получили дипломы, ![]() остальных участников были награждены похвальными
грамотами, а остальные 144 человека получили сертификаты об участии.
Сколько человек участвовало в олимпиаде?
остальных участников были награждены похвальными
грамотами, а остальные 144 человека получили сертификаты об участии.
Сколько человек участвовало в олимпиаде?
3. Задание 7 № 311961 На складе есть коробки с ручками двух цветов: чёрные и синие. Коробок с чёрными ручками 4, с синими — 11. Сколько всего ручек на складе, если чёрных ручек 640, коробки одинаковые и в каждой коробке находятся ручки только одного цвета?
4. Задание 7 № 316351 На молочном заводе пакеты молока упаковываются по 12 штук в коробку, причём в каждой коробке все пакеты одинаковые. В партии молока, отправляемой в магазин «Уголок», коробок с полуторалитровыми пакетами молока втрое меньше, чем коробок с литровыми пакетами. Сколько литров молока в этой партии, если коробок с литровыми пакетами молока 45?
5. Задание 7 № 317927 За 20 минут велосипедист проехал 7 километров. Сколько километров он проедет за 35 минут, если будет ехать с той же скоростью?
6. Задание 7 № 318245 Принтер печатает одну страницу за 12 секунд. Сколько страниц можно напечатать на этом принтере за 8 минут?
7. Задание 7 № 318265 Расстояние от Солнца до Юпитера равно 779 000 000 км. Сколько времени идёт свет от Солнца до Юпитера? Скорость света равна 300 000 км/с. Ответ дайте в минутах и округлите до десятых.
8. Задание 7 № 318273 Масштаб карты 1:100 000. Чему равно расстояние между городами A и B (в км), если на карте оно составляет 2 см?
9. Задание 7 № 318345 Расстояние от Солнца до Нептуна свет проходит примерно за 252,95 минуты. Найдите приблизительно расстояние от Солнца до Нептуна, ответ округлите до миллионов км. Скорость света равна 300 000 км/с.
10. Задание 7 № 337913 Из объявления фирмы, проводящей обучающие семинары:
«Стоимость участия в семинаре — 3000 р. с человека. Группам от организаций предоставляются скидки: от 3 до 10 человек — 5%; более 10 человек — 8%».
Сколько рублей должна заплатить организация, направившая на семинар группу из 4 человек?
11. Задание 7 № 338788 Поезд, двигаясь равномерно со скоростью 150 км/ч, проезжает мимо столба за 6 секунд. Найдите длину поезда в метрах.
12. Задание 7 № 341387 В начале года число абонентов телефонной компании «Восток» составляло 800 тыс. человек, а в конце года их стало 880 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
13. Задание 7 № 353264 Поезд, двигаясь равномерно со скоростью 150 км/ч, проезжает мимо столба за 18 секунд. Найдите длину поезда в метрах.
ЗАДАНИЕ 8
1. Задание 8 № 206051 На диаграмме показано распределения земель Уральского, Приволжского, Южного и Дальневосточного Федеральных округов по категориям. Определите по диаграмме, в каком округе доля земель лесного фонда превышает 70%.

*прочее — это земли поселений; земли промышленности и иного специального назначения; и земли особо охраняемых территорий и объектов.
1) Уральский ФО 2) Приволжский ФО 3) Южный ФО 4) Дальневосточный ФО
2. Задание 8 № 311296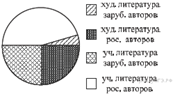 Фонд школьной библиотеки, состоящей из учебной и художественной
литературы российских и зарубежных авторов, представлен в виде
диаграммы. Сколько примерно книг учебной литературы в библиотеке, если всего
в библиотечном фонде 800 книг?
Фонд школьной библиотеки, состоящей из учебной и художественной
литературы российских и зарубежных авторов, представлен в виде
диаграммы. Сколько примерно книг учебной литературы в библиотеке, если всего
в библиотечном фонде 800 книг?
В ответе укажите номер правильного варианта.
1) 400 2) 570 3) 300 4) 600
3. Задание 8 № 311299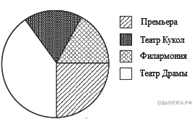 На диаграмме показано количество школьников, посетивших
театры г. Краснодара за 2010 г. Определите, сколько примерно зрителей
посетили за этот период Филармонию, если во всех этих театрах школьников
было 2000 человек.
На диаграмме показано количество школьников, посетивших
театры г. Краснодара за 2010 г. Определите, сколько примерно зрителей
посетили за этот период Филармонию, если во всех этих театрах школьников
было 2000 человек.
В ответе укажите номер правильного варианта.
1) 150 2) 240 3) 350 4) 500
4. Задание 8 № 311300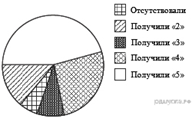 Учитель математики подвел итоги контрольной работы
по алгебре среди учащихся 9-х классов. Результаты представлены на
диаграмме. Сколько примерно учащихся получили отметку «4» и «5», если
всего в этих классах учатся 200 учащихся?
Учитель математики подвел итоги контрольной работы
по алгебре среди учащихся 9-х классов. Результаты представлены на
диаграмме. Сколько примерно учащихся получили отметку «4» и «5», если
всего в этих классах учатся 200 учащихся?
В ответе укажите номер правильного варианта. 1) 120 2) 50 3) 60 4) 140
5. Задание 8 № 311301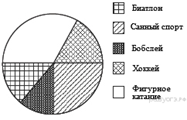 Учащимся сочинских школ был задан вопрос: «По какому
виду спорта вы хотели бы посетить соревнования на Зимней олимпиаде в
Сочи?». Их ответы можно увидеть на диаграмме. Сколько примерно учащихся
хотели бы посетить соревнования и по хоккею, и по санному спорту, если
всего в опросе приняли участие 400 школьников?
Учащимся сочинских школ был задан вопрос: «По какому
виду спорта вы хотели бы посетить соревнования на Зимней олимпиаде в
Сочи?». Их ответы можно увидеть на диаграмме. Сколько примерно учащихся
хотели бы посетить соревнования и по хоккею, и по санному спорту, если
всего в опросе приняли участие 400 школьников?
В ответе укажите номер правильного варианта. 1) 180 2) 240 3) 120 4) 200
6. Задание 8 № 311753На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каком продукте содержание белков превышает 30%.
*К прочему относятся вода, витамины и минеральные вещества.
1) какао 2) шоколад 3) фасоль 4) грибы
7. Задание 8 № 311906В математические кружки города ходят школьники 5–8 классов. Распределение участников математических кружков представлено в круговой диаграмме.
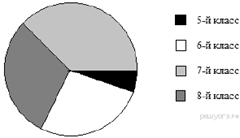 Какое утверждение относительно участников
кружков верно, если всего их посещают 354 школьника?
Какое утверждение относительно участников
кружков верно, если всего их посещают 354 школьника?
1) в кружки не ходят пятиклассники 2) восьмиклассников ходит больше, чем семиклассников
3) больше половины участников кружков учатся не в седьмом классе
4) шестиклассников меньше 88 человек
8. Задание 8 № 315142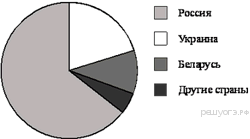 На диаграмме представлено распределение количества
пользователей некоторой социальной сети по странам мира. Всего в
этой социальной сети 12 млн пользователей.
На диаграмме представлено распределение количества
пользователей некоторой социальной сети по странам мира. Всего в
этой социальной сети 12 млн пользователей.
Какое из следующих утверждений неверно?
1) Пользователей из Украины больше, чем пользователей из Казахстана.
2) Пользователей из России вдвое больше, чем пользователей из Украины.
3) Примерно треть пользователей — не из России.
4) Пользователей из Украины и Беларуси более 3 млн человек.
9. Задание 8 № 316327На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каком продукте содержание жиров находится в пределах от 15% до 25%.
 *К прочему относятся вода, витамины
и минеральные вещества.
*К прочему относятся вода, витамины
и минеральные вещества.
1) какао 2) шоколад 3) фасоль 4) грибы
10. Задание 8 № 325289 На диаграмме показано содержание питательных веществ
в молочном шоколаде. Определите по диаграмме, содержание каких веществ
преобладает.
На диаграмме показано содержание питательных веществ
в молочном шоколаде. Определите по диаграмме, содержание каких веществ
преобладает.
*-к прочему относятся вода, витамины и минеральные вещества.
1) жиры 2) белки 3) углеводы 4) прочее В ответе запишите номер выбранного утверждения.
11. Задание 8 № 325311 В городе из учебных заведений имеются школы, колледжи,
училища и институты. Данные представлены на круговой диаграмме.
В городе из учебных заведений имеются школы, колледжи,
училища и институты. Данные представлены на круговой диаграмме.
Какое из утверждений относительно количества учебных заведений разных видов верно, если всего в городе 45 учебных заведений?
1) В городе более 30 школ. 2) В городе более трети всех учебных заведений — институты.
3) В городе
школ, колледжей и училищ более ![]() всех
учебных заведений.
всех
учебных заведений.
4) В городе примерно четверть всех учебных заведений — училища.
12. Задание 8 № 325316 Участников конференции разместили в гостинице в
одноместных номерах, расположенных на этажах со второго по пятый.
Количество номеров на этажах представлено на круговой диаграмме.
Участников конференции разместили в гостинице в
одноместных номерах, расположенных на этажах со второго по пятый.
Количество номеров на этажах представлено на круговой диаграмме.
Какое из утверждений относительно расселения участников конференции неверно, если в гостинице разместились 80 участников конференции?
1) Более 20 участников конференции разместились на втором этаже.
2) На 2, 4 и 5 этажах разместились меньше половины участников конференции.
3) На этажах выше третьего разместились не более четверти всех участников конференции.
4) На втором и третьем этаже разместились не менее 75% всех участников конференции.
13. Задание 8 № 325319 В доме располагаются однокомнатные, двухкомнатные,
трёхкомнатные и четырёхкомнатные квартиры. Данные о количестве квартир
представлены на круговой диаграмме.
В доме располагаются однокомнатные, двухкомнатные,
трёхкомнатные и четырёхкомнатные квартиры. Данные о количестве квартир
представлены на круговой диаграмме.
Какие из утверждений относительно квартир в этом доме неверны, если всего в доме 180 квартир?
1) Больше половины квартир двухкомнатные. 2) Однокомнатных квартир менее четверти.
3) Четверть всех квартир — трёхкомнатные.
4) Однокомнатных, двухкомнатных и трёхкомнатных квартир всего более 165.
В ответе запишите номера выбранных утверждений.
14. Задание 8 № 325324 В математический кружок ходят школьники 5−8
классов. Данные о количестве школьников, посещающих кружок, представлены
на круговой диаграмме. Какое утверждение относительно участников
кружка верно, если всего его посещают 60 школьников?
В математический кружок ходят школьники 5−8
классов. Данные о количестве школьников, посещающих кружок, представлены
на круговой диаграмме. Какое утверждение относительно участников
кружка верно, если всего его посещают 60 школьников?
1) Больше трети школьников восьмиклассники. 2) Пятиклассников меньше, чем семиклассников.
3) Семиклассников больше 7 человек. 4)Шестиклассников больше 50% всех школьников.
15. Задание 8 № 325325 На диаграмме показано содержание питательных веществ
в какао-порошке. Определите по диаграмме, содержание каких веществ
наименьшее.
На диаграмме показано содержание питательных веществ
в какао-порошке. Определите по диаграмме, содержание каких веществ
наименьшее.
*-к прочему относятся вода, витамины и минеральные вещества.
1) жиры 2) белки 3) углеводы 4) прочее
16. Задание 8 № 325342 На диаграмме показано содержание питательных веществ
в молочном шоколаде. Определите по диаграмме, содержание каких веществ
превосходит 50%.
На диаграмме показано содержание питательных веществ
в молочном шоколаде. Определите по диаграмме, содержание каких веществ
превосходит 50%.
*-к прочему относятся вода, витамины и минеральные вещества.
1) жиры 2) белки 3) углеводы 4) прочее
17. Задание 8 № 325362 На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сливочных сухарях. Определите по диаграмме, в каком продукте содержание углеводов наибольшее.
*-к прочему относятся вода, витамины и минеральные вещества.

1) какао 2) шоколад 3) фасоль 4) сухари
18. Задание 8 № 325372 На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сливочных сухарях. Определите по диаграмме, в каком продукте содержание углеводов наименьшее.
1) какао 2) шоколад 3) фасоль 4) сухари
19. Задание 8 № 325392 На диаграмме показаны религиозные составы населения Германии, США, Австрии и Великобритании. Определите по диаграмме, в какой стране доля католиков превышает 50%.
1) Германия 2) США 3) Австрия 4) Великобритания
20. Задание 8 № 325396
 На диаграмме показано содержание
питательных веществ в сливочных сухарях. Определите по диаграмме,
в каких пределах находится содержание углеводов.
На диаграмме показано содержание
питательных веществ в сливочных сухарях. Определите по диаграмме,
в каких пределах находится содержание углеводов.
*-к прочему относятся вода, витамины и минеральные вещества.
1) 45-55% 2) 55-65% 3) 65-75% 4) 75-80%
21. Задание 8 № 325415 На диаграмме показан возрастной состав населения
Китая.
На диаграмме показан возрастной состав населения
Китая.
Сколько примерно людей младше 14 лет проживает в Китае, если население Китая составляет 1,3 млрд людей?
1) около 100 млн 2) около 260 млн 3) около 325 млн 4) около 150 млн
22. Задание 8 № 325886 Какая из следующих круговых диаграмм показывает распределение площадей океанов в Мировом Океане, если Тихий Океан занимает около 48% всего Мирового Океана, Атлантический — 26%, Индийский — 21% и Северный Ледовитый — 5%?
23. Задание 8 № 340595 Завуч школы подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на круговой диаграмме.
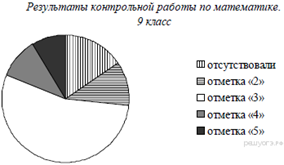
Какие из утверждений относительно результатов контрольной работы верны, если всего в школе 120 девятиклассников? В ответе укажите номера верных утверждений.
1) Более половины учащихся получили отметку «3».
2) Около половины учащихся отсутствовали на контрольной работе или получили отметку «2».
3) Отметку «4» или «5» получила примерно шестая часть учащихся.
4) Отметку «3», «4» или «5» получили более 100 учащихся.
24. Задание 8 № 341590 Завуч школы подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на круговой диаграмме.
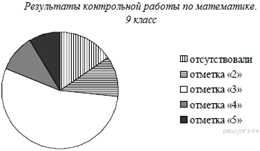
Какие из утверждений относительно результатов контрольной работы верны, если всего в школе 120 девятиклассников? В ответе укажите номера верных утверждений.
1) Более половины учащихся получили отметку «3».
2) Около половины учащихся отсутствовали на контрольной работе или получили отметку «2».
3) Отметку «4» или «5» получила примерно шестая часть учащихся.
4) Отметку «3», «4» или «5» получили более 100 учащихся.
25. Задание 8 № 343126Завуч школы подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на круговой диаграмме.
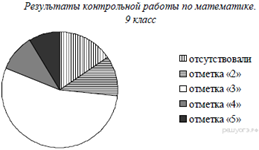 Какие из утверждений
относительно результатов контрольной работы верны, если всего в
школе 120 девятиклассников? В ответе укажите номера верных утверждений.
Какие из утверждений
относительно результатов контрольной работы верны, если всего в
школе 120 девятиклассников? В ответе укажите номера верных утверждений.
1) Более половины учащихся получили отметку «3».
2) Около половины учащихся отсутствовали на контрольной работе или получили отметку «2».
3) Отметку «4» или «5» получила примерно шестая часть учащихся.
4) Отметку «3», «4» или «5» получили более 100 учащихся.
1. Задание 8 № 109На диаграмме представлены семь крупнейших по площади
территории (в млн км2) стран мира.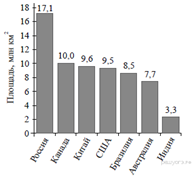 Какое из следующих утверждений неверно?
Какое из следующих утверждений неверно?
1) Площадь территории Индии составляет ![]() 2) Площадь Китая больше площади Австралии 3) Россия — крупнейшая по
площади территории страна мира.
2) Площадь Китая больше площади Австралии 3) Россия — крупнейшая по
площади территории страна мира.
4) Площадь Канады больше площади США
на ![]()
2. Задание 8 № 311314 156
учащимся восьмых классов некоторой школы была предложена контрольная
работа по алгебре из 5 заданий. По результатам составили таблицу, в
которой указали число учащихся, выполнивших одно, два три и т.д.
заданий: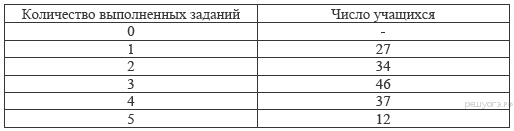 Сколько человек получили оценку выше «3», если критерии
выставления оценок определялись по таблице?
Сколько человек получили оценку выше «3», если критерии
выставления оценок определялись по таблице?![]()
3. Задание 8 № 311916 На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за последние два часа программы по сравнению с первыми двумя часами этой программы.
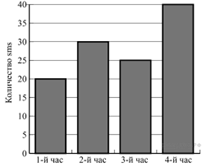
4. Задание 8 № 315139
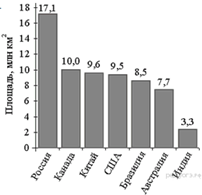 На диаграмме представлены семь крупнейших
по площади территории (в млн км2) стран мира.
На диаграмме представлены семь крупнейших
по площади территории (в млн км2) стран мира.
Какое из следующих утверждений верно?
1) Казахстан входит в семёрку крупнейших по площади территории стран мира.
2) Площадь территории Бразилии составляет 8,5 млн км2.
3) Площадь Австралии больше площади Китая.
4) Площадь Бразилии больше площади Индии более чем в три раза.
5. Задание 8 № 315165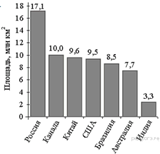 На диаграмме представлены семь крупнейших по площади
территории (в млн км2) стран мира.
На диаграмме представлены семь крупнейших по площади
территории (в млн км2) стран мира.
Какое из следующих утверждений неверно?
1) Россия — крупнейшая по площади территории страна мира.
2) Площадь территории Индии составляет 3,3 млн км2.
3) Площадь Китая больше площади Австралии.
4) Площадь Канады больше площади США на 1,5 млн км2.
6. Задание 8 № 315176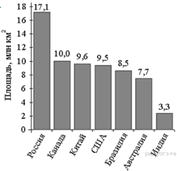 На диаграмме представлены семь крупнейших по площади
территории (в млн км2) стран мира. Какое из следующих утверждений
неверно?
На диаграмме представлены семь крупнейших по площади
территории (в млн км2) стран мира. Какое из следующих утверждений
неверно?
1) По площади территории второе место в мире занимает Канада.
2) Площадь территории Австралии составляет 7,7 млн км2.
3) Площадь Китая больше площади Канады.
4) Площадь США больше площади Бразилии на 1 млн км2.
7. Задание 8 № 315199 На диаграмме представлены некоторые из крупнейших по численности населения стран мира. Численность населения какого государства примерно в 6 раз меньше численности населения Индии? В ответе напишите численность населения этой страны в млн чел.
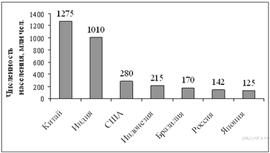
8. Задание 8 № 315207На диаграмме представлены некоторые из крупнейших по площади территории стран мира. Во сколько примерно раз площадь России больше площади США? (Ответ округлите до целых.)
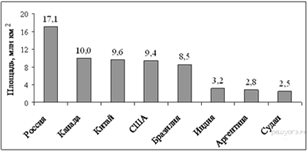
9. Задание 8 № 316379 Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме.
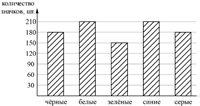
Определите по диаграмме, значков какого цвета было продано меньше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета?
1) 5 2) 10 3) 15 4) 20
10. Задание 8 № 325287 На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за первые два часа программы по сравнению с последними двумя часами этой программы.
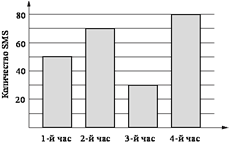
11. Задание 8 № 325747 На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за последние два часа программы по сравнению с первыми двумя часами этой программы.
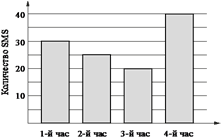
ЗАДАНИЕ 9
1. Задание 9 № 149 На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет.
2. Задание 9 № 132728 Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
3. Задание 9 № 132730 Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.
4. Задание 9 № 132732 На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
5. Задание 9 № 132734 В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
6. Задание 9 № 132736 В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.
7. Задание 9 № 132738 Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке.
8. Задание 9 № 132740 У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
9. Задание 9 № 132744 Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.
10. Задание 9 № 132748 В среднем из каждых 80 поступивших в продажу аккумуляторов 76 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.
11. Задание 9 № 311324 Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
12. Задание 9 № 311336 В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
13. Задание 9 № 311359 В денежно-вещевой лотерее на 100 000 билетов разыгрывается 1300 вещевых и 850 денежных выигрышей. Какова вероятность получить вещевой выигрыш?
14. Задание 9 № 311415 Из 900 новых флеш-карт в среднем 54 не пригодны для записи. Какова вероятность того, что случайно выбранная флеш-карта пригодна для записи?
15. Задание 9 № 311505 В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?
16. Задание 9 № 311512 В группе из 20 российских туристов несколько человек владеют иностранными языками. Из них пятеро говорят только по-английски, трое только по-французски, двое по-французски и по-английски. Какова вероятность того, что случайно выбранный турист говорит по-французски?
17. Задание 9 № 311525 В коробке 14 пакетиков с чёрным чаем и 6 пакетиков с зелёным чаем. Павел наугад вынимает один пакетик. Какова вероятность того, что это пакетик с зелёным чаем?
18. Задание 9 № 311767 Стас, Денис, Костя, Маша, Дима бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.
19. Задание 9 № 311919 Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А.
20. Задание 9 № 315159 В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.
21. Задание 9 № 315173 В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
22. Задание 9 № 315195 Из каждых 1000 электрических лампочек 5 бракованных. Какова вероятность купить исправную лампочку?
23. Задание 9 № 316328Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
24. Задание 9 № 325436Из 1600 пакетов молока в среднем 80 протекают. Какова вероятность того, что случайно выбранный пакет молока не течёт?
25. Задание 9 № 325450В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
26. Задание 9 № 325453Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.
27. Задание 9 № 325481Определите вероятность того, что при бросании кубика выпало число очков, не большее 3.
28. Задание 9 № 325482В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно 1 раз.
29. Задание 9 № 325491Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
30. Задание 9 № 325540Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
31. Задание 9 № 325560В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
|
Номер стрелка |
Число выстрелов |
Число попаданий |
|
1 |
42 |
28 |
|
2 |
70 |
20 |
|
3 |
54 |
45 |
|
4 |
46 |
42 |
Тренер решил послать на соревнования того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите в ответе его номер.
32. Задание 9 № 325580 В магазине канцтоваров продаётся 100 ручек, из них 37 – красные, 8 – зелёные, 17 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку.
33. Задание 9 № 341531В среднем из 100 карманных фонариков, поступивших в продажу, восемь неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
1. Задание 9 № 315196 Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
2. Задание 9 № 316354Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два случайно выбранных из одной партии фонарика окажутся небракованными?
3. Задание 9 № 325288Средний рост жителя города, в котором живет Даша, равен 170 см. Рост Даши 173 см. Какое из следующих утверждений верно?
1) Даша — самая высокая девушка в городе. 2) Обязательно найдется девушка ниже 170 см.
3) Обязательно найдется человек ростом менее 171 см. 4) Обязательно найдется человек ростом 167 см.
4. Задание 9 № 325454 Известно, что в некотором регионе вероятность того, что родившийся младенец окажется мальчиком, равна 0,512. В 2010 г. в этом регионе на 1000 родившихся младенцев в среднем пришлось 477 девочек. Насколько частота рождения девочек в 2010 г. в этом регионе отличалась от вероятности этого события?
5. Задание 9 № 325457 Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
6. Задание 9 № 340463 На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
7. Задание 9 № 341364Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.
ЗАДАНИЕ 10
1. Задание 10 № 193089 Найдите
значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.
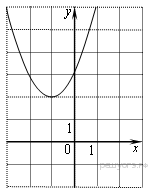
|
1) |
2) |
3) |
4) |
2. Задание 10 № 193090 Найдите значение ![]() по
графику функции
по
графику функции ![]() ,
изображенному на рисунке.
,
изображенному на рисунке.
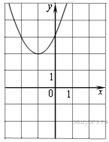
|
1) |
2) |
3) |
4) |
3. Задание 10 № 193091 Найдите
значение ![]() по
графику функции
по
графику функции ![]() изображенному
на рисунке.
изображенному
на рисунке.
|
|
2) |
3) |
4) |
4. Задание 10 № 193102 Найдите
значение ![]() по графику функции
по графику функции ![]() изображенному на рисунке.
изображенному на рисунке.
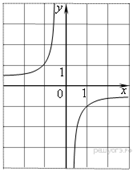
5. Задание 10 № 311406 На
рисунке изображён график функции ![]() . Какие из утверждений относительно этой функции
неверны? Укажите их номера.
. Какие из утверждений относительно этой функции
неверны? Укажите их номера.
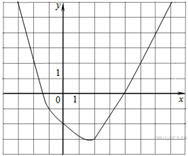
1) функция возрастает на промежутке
![]() 2)
2) ![]()
3) ![]() 4) прямая
4) прямая ![]() пересекает график в точках
пересекает график в точках ![]() и
и ![]()
6. Задание 10 № 314676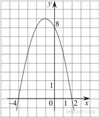
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера в порядке возрастания.
1) Функция возрастает на промежутке (−∞; −1]. 2) Наибольшее значение функции равно 8.
3) f(−4) ≠ f(2).
7. Задание 10 № 314703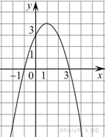
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(−1) = f(3). 2) Наибольшее значение функции равно 3. 3) f(x)>0 при −1<x<3.
8. Задание 10 № 31470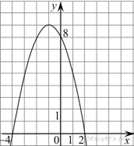
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Наибольшее значение функции равно 9. 2) f(0)>f(1). 3) f( x )>0 при x<0.
9. Задание 10 № 333008 На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
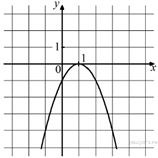
|
УТВЕРЖДЕНИЯ |
|
ПРОМЕЖУТКИ |
|
А) функция возрастает на промежутке Б) функция убывает на промежутке |
|
1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3] |
10. Задание 10 № 333087 На
рисунке изображён график функции вида ![]() . Установите соответствие между утверждениями и
промежутками, на которых эти утверждения выполняются. Впишите в
приведённую в ответе таблицу под каждой буквой соответствующую
цифру.
. Установите соответствие между утверждениями и
промежутками, на которых эти утверждения выполняются. Впишите в
приведённую в ответе таблицу под каждой буквой соответствующую
цифру.
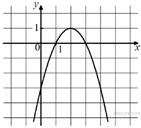
|
УТВЕРЖДЕНИЯ |
|
ПРОМЕЖУТКИ |
|
А) функция возрастает на промежутке Б) функция убывает на промежутке |
|
1) [0; 3] 2) [−1; 1] 3) [2; 4] 4) [1; 4] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
11. Задание 10 № 339184На рисунке изображены графики функций вида y = ax2 + bx + c. Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D.
|
ГрафикиА)
|
Б)
|
В)
|
Г)
|
Знаки чисел
|
1) a > 0, D > 0 |
2) a > 0, D < 0 |
3) a < 0, D > 0 |
4) a < 0, D < 0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
1. Задание 10 № 34 Установите соответствие между графиками функций и формулами, которые их задают.
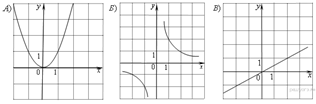 1)
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Задание 10 № 193087График какой из приведенных ниже функций изображен на рисунке?
|
|
2) |
3) |
4) |
3. Задание 10 № 193093 На
одном из рисунков изображен график функции ![]() . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
|
1) |
|
2) |
|
|
3) |
|
4) |
|
4. Задание 10 № 193097 На одном из рисунков изображена парабола. Укажите номер этого рисунка.
|
1) |
|
2) |
|
|
3) |
|
4) |
|
6. Задание 10 № 200515 На
одном из рисунков изображен график функции ![]() . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
|
|
1) |
2) |
|
|
3) |
4) |
7. Задание 10 № 201145 На
одном из рисунков изображен график функции ![]() . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
|
|
1) |
2) |
|
|
3) |
4) |
8. Задание 10 № 202195 На одном из рисунков изображена гипербола. Укажите номер этого рисунка.
|
|
1) |
2) |
|
|
3) |
4) |
9. Задание 10 № 314771Установите соответствие между графиками функций и формулами, которые их задают.
Графики
|
А) |
Б) |
В) |
|
|
|
|
Формулы
|
1) |
2) |
3) |
4) |
10. Задание 10 № 31477Установите соответствие между графиками функций и формулами, которые их задают. Графики
|
А) |
Б) |
В) |
|
|
|
|
Формулы
|
1) |
2) |
3) |
4) |
11. Задание 10 № 31636Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)![]() Б)
Б)![]() В)
В)![]() ГРАФИКИ
ГРАФИКИ
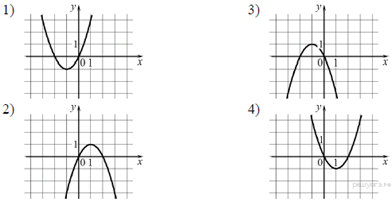
12. Задание 10 № 32186На рисунке изображены графики функций вида y = ax2 + c. Установите соответствие между графиками и знаками коэффициентов a и c.
ГРАФИКИ
|
А) |
Б) |
В) |
Г) |
|
|||
|
ЗНАКИ КОЭФФИЦИЕНТОВ 1) a > 0, c < 0 |
2) a < 0, c > 0 |
3) a > 0, c > 0 |
4) a < 0, c < 0 |
||||
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
13. Задание 10 № 32191Установите соответствие между графиками функций и формулами, которые их задают.
|
А)
|
Б)
|
В)
|
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
14. Задание 10 № 32192Установите соответствие между графиками функций и формулами, которые их задают.
|
А)
|
Б)
|
В)
|
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
15. Задание 10 № 322008Установите соответствие между графиками функций и формулами, которые их задают.
|
А)
|
Б)
|
В)
|
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
16. Задание 10 № 339073Установите соответствие между функциями и их графиками.
Функции
|
А) |
Б) |
В) |
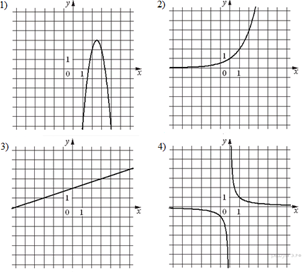
17. Задание 10 № 339091Установите соответствие между функциями и их графиками.
Функции
|
А) y = −2x + 4 |
Б) y = 2x – 4 |
В) y= 2x + 4 |
Графики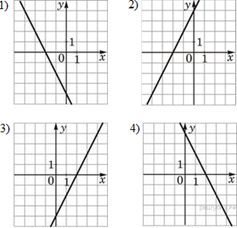
18. Задание 10 № 339114Установите соответствие между функциями и их графиками.
Функции
|
А) |
Б) |
В) |
Графики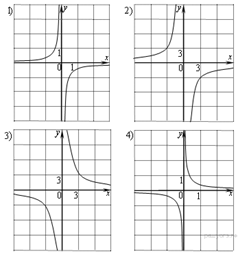
19. Задание 10 № 339254На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты
|
А) a > 0, c < 0 |
Б) a < 0, c > 0 |
В) a > 0, c > 0 |
|
|
Графики1)
|
2)
|
||
|
3)
|
4)
|
||
20. Задание 10 № 341325На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
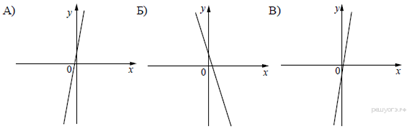
|
1) k < 0, b > 0 |
2) k > 0, b > 0 |
3) k < 0, b < 0 |
4) k > 0, b < 0 |
Задание 11
Числовые последовательности
1. Задание 11 № 137294Последовательность задана формулой ![]() . Какое из указанных чисел является членом этой
последовательности?
. Какое из указанных чисел является членом этой
последовательности?
|
1) 1 |
2) 2 |
3) 3 |
4) 4 |
2. Задание 11 № 137295Последовательность задана формулой ![]() . Какое из следующих чисел не является членом этой
последовательности?
. Какое из следующих чисел не является членом этой
последовательности?
|
1) |
2) |
3) |
4) |
3. Задание 11 № 137296Какое из указанных чисел не является членом последовательности ![]()
|
1) |
2) |
3) |
4) |
4. Задание 11 № 137297Последовательность задана формулой ![]() . Сколько членов в этой последовательности больше
1?
. Сколько членов в этой последовательности больше
1?
|
1) 8 |
2) 9 |
3) 10 |
4) 11 |
5. Задание 11 № 137298Последовательности заданы несколькими первыми членами. Одна из них — арифметическая прогрессия. Укажите ее.
|
1) |
2) |
3) |
4) |
6. Задание 11 № 137299Одна из данных последовательностей является геометрической прогрессией. Укажите эту последовательность.
|
1) |
2) |
3) |
4) |
7. Задание 11 № 137300Какая из следующих последовательностей является арифметической прогрессией?
|
1) Последовательность натуральных степеней числа 2. |
|
2) Последовательность натуральных чисел, кратных 5. |
|
3) Последовательность кубов натуральных чисел. |
|
4) Последовательность всех правильных дробей, числитель которых на 1 меньше знаменателя. |
8. Задание 11 № 137306Последовательность задана условиями ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
9. Задание 11 № 137307Последовательность задана условиями ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
10. Задание 11 № 169365Последовательность задана формулой ![]() . Какое из следующих чисел не является членом этой
последовательности?
. Какое из следующих чисел не является членом этой
последовательности?
|
1) −2 |
2) |
3) |
4) 2 |
11. Задание 11 № 341203Последовательность задана формулой ![]() Сколько членов в этой последовательности больше
6?
Сколько членов в этой последовательности больше
6?
12. Задание 11 № 341669Сколько натуральных чисел n удовлетворяет
неравенству ![]()
13. Задание 11 № 351753Последовательность задана формулой ![]() Сколько членов в этой последовательности больше
3?
Сколько членов в этой последовательности больше
3?
Арифметическая прогрессия
1. Задание 11 № 35Дана арифметическая прогрессия: ![]() Найдите сумму первых десяти её членов.
Найдите сумму первых десяти её членов.
2. Задание 11 № 113Дана арифметическая прогрессия ![]() Найдите
Найдите ![]() .
.
3. Задание 11 № 165Дана арифметическая прогрессия ![]() Найдите сумму первых десяти её членов.
Найдите сумму первых десяти её членов.
4. Задание 11 № 137301Выписаны первые несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии?
|
1) 83 |
2) 95 |
3) 100 |
4) 102 |
5. Задание 11 № 13730Арифметические прогрессии ![]() ,
, ![]() и
и ![]() заданы формулами n-го члена:
заданы формулами n-го члена: ![]() ,
, ![]() ,
, ![]() Укажите те из них, у которых разность
Укажите те из них, у которых разность ![]() равна 4.
равна 4.
|
1) |
2) |
3) |
4) |
6. Задание 11 № 137303В первом ряду кинозала 30 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером n?
|
1) |
2) |
3) |
4) |
7. Задание 11 № 137304Дана арифметическая прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии.
|
1) |
2) |
3) |
4) |
8. Задание 11 № 137305Арифметическая прогрессия задана условиями:![]() ,
, ![]() . Какое из данных чисел является членом этой
прогрессии?
. Какое из данных чисел является членом этой
прогрессии?
|
1) 80 |
2) 56 |
3) 48 |
4) 32 |
9. Задание 11 № 311254Найдите сумму всех отрицательных членов арифметической прогрессии: −8,6; −8,4; ...
10. Задание 11 № 311330Арифметическая прогрессия ![]() задана формулой n-го члена
задана формулой n-го члена ![]() и известно, что
и известно, что ![]() . Найдите пятый член этой прогрессии.
. Найдите пятый член этой прогрессии.
11. Задание 11 № 311363В арифметической прогрессии ![]() известно, что
известно, что ![]() . Найдите четвёртый член этой прогрессии.
. Найдите четвёртый член этой прогрессии.
12. Задание 11 № 311909Арифметическая прогрессия задана условиями: ![]()
![]() . Найдите сумму первых 19 её членов.
. Найдите сумму первых 19 её членов.
13. Задание 11 № 314399Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 528?
14. Задание 11 № 314408Найдите сумму всех положительных членов арифметической прогрессии 11,2; 10,8; …
15. Задание 11 № 314423Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы получившаяся сумма была больше 465?
16. Задание 11 № 314425Найдите сумму всех отрицательных членов арифметической прогрессии –7,2; –6,9; …
17. Задание 11 № 314619Арифметическая прогрессия (an) задана условиями: a1 = 3, an + 1 = an + 4. Найдите a10.
18. Задание 11 № 314628Записаны первые три члена арифметической прогрессии: 20; 17; 14. Какое число стоит в этой арифметической прогрессии на 91-м месте?
19. Задание 11 № 314653Дана арифметическая прогрессия (аn): −6; −2; 2; … . Найдите a16.
20. Задание 11 № 316343Выписаны первые несколько членов арифметической прогрессии: −87 ; −76; −65; … Найдите первый положительный член этой прогрессии.
21. Задание 11 № 321384В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
22. Задание 11 № 321394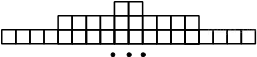 Фигура составляется из квадратов так, как показано
на рисунке: в каждой следующей строке на 8 квадратов больше, чем в
предыдущей. Сколько квадратов в 16-й строке?
Фигура составляется из квадратов так, как показано
на рисунке: в каждой следующей строке на 8 квадратов больше, чем в
предыдущей. Сколько квадратов в 16-й строке?
23. Задание 11 № 321663Выписано несколько последовательных членов арифметической прогрессии: …; −9; x; −13; −15; … Найдите член прогрессии, обозначенный буквой x .
24. Задание 11 № 339063Дана арифметическая прогрессия (an), разность которой равна 2,5, a1 = 8,7. Найдите a9.
25. Задание 11 № 340584Даны пятнадцать чисел, первое из которых равно 6, а каждое следующее больше предыдущего на 4. Найти пятнадцатое из данных чисел.
26. Задание 11 № 341190Дана арифметическая прогрессия (an), разность которой равна −8,5, a1 = −6,8. Найдите a11.
27. Задание 11 № 341201Арифметическая прогрессия ![]() задана условиями:
задана условиями: ![]() Найдите
Найдите ![]()
28. Задание 11 № 341202Дана арифметическая прогрессия (an), для которой a10 = 19, a15 = 44. Найдите разность прогрессии.
29. Задание 11 № 341214Арифметическая прогрессия задана условием an = −0,6 + 8,6n. Найдите сумму первых 10 её членов.
30. Задание 11 № 341221Дана арифметическая прогрессия (an), разность которой равна −2,5, a1 = −9,1. Найдите сумму первых 15 её членов.
31. Задание 11 № 341492Арифметическая прогрессия задана условием an = −11,9 + 7,8n . Найдите a11.
32. Задание 11 № 341518Первый член арифметической прогрессии равен −11,9, а разность прогрессии равна 7,8. Найдите двенадцатый член этой прогрессии.
33. Задание 11 № 341703Дан числовой набор. Его первое число равно 6,2, а каждое следующее число на 0,6 больше предыдущего. Найдите пятое число этого набора.
34. Задание 11 № 353273Выписаны первые несколько членов арифметической прогрессии: −26 ; −20; −14; … Найдите первый положительный член этой прогрессии.
35. Задание 11 № 353405Дана арифметическая прогрессия (an), разность которой равна 1,1, a1 = −7. Найдите сумму первых 8 её членов.
36. Задание 11 № 353486Арифметическая прогрессия задана условием an = 1,9 - 0,3n. Найдите сумму первых 15 её членов.
Геометрическая прогрессия
1. Задание 11 № 311318В геометрической прогрессии ![]() известно, что
известно, что ![]() . Найти пятый член этой прогрессии.
. Найти пятый член этой прогрессии.
2. Задание 11 № 311353Геометрическая прогрессия ![]() задана формулой
задана формулой ![]() - го члена
- го члена ![]() . Укажите четвертый член этой прогрессии.
. Укажите четвертый член этой прогрессии.
3. Задание 11 № 311953Дана геометрическая прогрессия (bn),
знаменатель которой равен 2, а ![]() . Найдите сумму первых шести её членов.
. Найдите сумму первых шести её членов.
4. Задание 11 № 314618В геометрической прогрессии сумма первого и второго членов равна 75, а сумма второго и третьего членов равна 150. Найдите первые три члена этой прогрессии.
В ответе запишите первый, второй и третий члены прогрессии без пробелов.
5. Задание 11 № 321377Геометрическая прогрессия задана условием ![]() Найдите сумму первых её 4 членов.
Найдите сумму первых её 4 членов.
6. Задание 11 № 321553Выписаны первые несколько членов геометрической прогрессии: 17, 68, 272, ... Найдите её четвёртый член.
7. Задание 11 № 321687Выписано несколько последовательных членов геометрической прогрессии: … ; 150 ; x ; 6 ; 1,2 ; … Найдите член прогрессии, обозначенный буквой x.
8. Задание 11 № 333009Выписаны первые несколько членов геометрической прогрессии: −1024; −256; −64; … Найдите сумму первых 5 её членов.
9. Задание 11 № 341191Геометрическая прогрессия задана условием ![]() Найдите сумму первых её 4 членов.
Найдите сумму первых её 4 членов.
10. Задание 11 № 341197Выписано несколько последовательных членов геометрической прогрессии: … ; 1,75; x; 28 ; −112; … Найдите член прогрессии, обозначенный буквой x.
11. Задание 11 № 341198Дана геометрическая прогрессия (bn), для которой b5 = −14, b8 = 112. Найдите знаменатель прогрессии.
12. Задание 11 № 341206Геометрическая прогрессия задана условием b1 = −7, bn + 1 = 3bn. Найдите сумму первых 5 её членов.
13. Задание 11 № 341208Дана геометрическая прогрессия (bn), знаменатель которой равен 2, а b1 = 16. Найдите b4.
14. Задание 11 № 341217Дана геометрическая прогрессия (bn),
знаменатель которой равен 5, а ![]() Найдите сумму первых 6 её членов.
Найдите сумму первых 6 её членов.
15. Задание 11 № 341220Выписаны первые несколько членов геометрической прогрессии: − 256; 128; − 64; … Найдите сумму первых семи её членов.
16. Задание 11 № 353212Дана геометрическая прогрессия (bn),
для которой b3 = ![]() , b6 = -196. Найдите знаменатель
прогрессии.
, b6 = -196. Найдите знаменатель
прогрессии.
17. Задание 11 № 353420Геометрическая прогрессия задана условием b1 = −3, bn + 1 = 6bn. Найдите сумму первых 4 её членов.
18. Задание 11 № 353437Выписано несколько поседовательных членов геометрической прогрессии: … ; -12 ; x ; -3 ; 1,5 ; … Найдите член прогрессии, обозначенный буквой x.
Целые выражения
1. Задание 12 № 36Упростите выражение ![]() , найдите его значение при
, найдите его значение при ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
2. Задание 12 № 311383Найдите значение выражения ![]() при
при ![]()
3. Задание 12 № 311910
Найдите значение
выражения ![]() при
при ![]()
4. Задание 12 № 338067
Найдите значение
выражения ![]() при
при ![]()
5. Задание 12 № 338092
Найдите ![]() если
если ![]()
6. Задание 12 № 338423
Найдите значение выражения ![]() при
при ![]()
Рациональные выражения
1. Задание 12 № 140Упростите выражение ![]() , найдите его значение при
, найдите его значение при ![]() ;
; ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
2. Задание 12 № 311329Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
3. Задание 12 № 311352Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
4. Задание 12 № 311372Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
5. Задание 12 № 311451Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() . В ответе запишите найденное значение.
. В ответе запишите найденное значение.
6. Задание 12 № 311463Представьте в виде дроби выражение ![]() и найдите его значение при
и найдите его значение при ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
7. Задание 12 № 311467Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() . В ответе запишите полученное число.
. В ответе запишите полученное число.
8. Задание 12 № 311471Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]()
9. Задание 12 № 311758Найдите значение выражения ![]() при
при ![]()
10. Задание 12 № 311814Найдите значение выражения ![]() при
при ![]()
11. Задание 12 № 311954Найдите значение выражения ![]() при
при ![]()
12. Задание 12 № 314312Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() В ответе запишите найденное значение.
В ответе запишите найденное значение.
13. Задание 12 № 314315Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() и
и ![]() В ответе запишите найденное значение.
В ответе запишите найденное значение.
14. Задание 12 № 316255Найдите значение выражения ![]() при а = 6.
при а = 6.
15. Задание 12 № 316344Сократите дробь ![]()
16. Задание 12 № 318572Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]()
![]() В ответе запишите найденное значение.
В ответе запишите найденное значение.
17. Задание 12 № 319060Найдите значение выражения ![]() при
при ![]()
![]()
18. Задание 12 № 319072Найдите значение выражения ![]() при
при ![]()
![]()
19. Задание 12 № 338076Найдите значение выражения 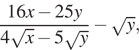 если
если ![]()
20. Задание 12 № 338095Найдите значение выражения ![]() при
при ![]()
21. Задание 12 № 338131Найдите значение выражения ![]() при
при ![]()
22. Задание 12 № 338163Найдите значение выражения ![]() при
при ![]()
23. Задание 12 № 338181Найдите значение выражения ![]() при
при ![]()
24. Задание 12 № 338274Найдите значение выражения ![]() при
при ![]()
25. Задание 12 № 338448Найдите значение выражения ![]() при
при ![]()
26. Задание 12 № 341353Найдите значение выражения ![]() при a = 78, c = 21.
при a = 78, c = 21.
27. Задание 12 № 341704Найдите значение выражения ![]() при a = 7,7.
при a = 7,7.
28. Задание 12 № 350738Найдите значение выражения: 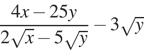 , если
, если ![]()
Вычисление по формуле
1. Задание 13 № 202В фирме «Эх, прокачу!» стоимость поездки на такси (в
рублях) рассчитывается по формуле ![]() , где
, где ![]() — длительность поездки, выраженная в минутах
— длительность поездки, выраженная в минутах ![]() . Пользуясь этой формулой, рассчитайте стоимость
8-минутной поездки.
. Пользуясь этой формулой, рассчитайте стоимость
8-минутной поездки.
2. Задание 13 № 311326Площадь параллелограмма ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где
, где ![]() — стороны параллелограмма (в метрах). Пользуясь
этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12
м и
— стороны параллелограмма (в метрах). Пользуясь
этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12
м и ![]() .
.
3. Задание 13 № 311533В фирме «Чистая вода» стоимость (в рублях) колодца из
железобетонных колец рассчитывается по формуле ![]() , где
, где ![]() — число колец, установленных при рытье колодца.
Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
— число колец, установленных при рытье колодца.
Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
4. Задание 13 № 338071Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 80 см, n = 1600? Ответ выразите в километрах.
5. Задание 13 № 338396Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
6. Задание 13 № 341532Из формулы центростремительного ускорения a = ω2R найдите R (в метрах), если ω = 4 с−1 и a = 64 м/с2.
Линейные уравнения
1. Задание 13 № 311337Длину окружности ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где
, где ![]() — радиус окружности (в метрах). Пользуясь этой
формулой, найдите радиус окружности, если её длина равна 78 м.
(Считать
— радиус окружности (в метрах). Пользуясь этой
формулой, найдите радиус окружности, если её длина равна 78 м.
(Считать ![]() ).
).
2. Задание 13 № 311348Площадь ромба ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где
, где ![]() — диагонали ромба (в метрах). Пользуясь
этой формулой, найдите диагональ
— диагонали ромба (в метрах). Пользуясь
этой формулой, найдите диагональ ![]() , если диагональ
, если диагональ ![]() равна 30 м, а площадь ромба 120 м2.
равна 30 м, а площадь ромба 120 м2.
3. Задание 13 № 311528Площадь треугольника ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где
, где ![]() — сторона треугольника,
— сторона треугольника, ![]() — высота, проведенная к этой стороне (в метрах).
Пользуясь этой формулой, найдите сторону
— высота, проведенная к этой стороне (в метрах).
Пользуясь этой формулой, найдите сторону ![]() , если площадь треугольника равна
, если площадь треугольника равна ![]() , а высота
, а высота ![]() равна 14 м.
равна 14 м.
4. Задание 13 № 311530Площадь трапеции ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где
, где ![]() — основания трапеции,
— основания трапеции, ![]() — высота (в метрах). Пользуясь этой формулой, найдите
высоту
— высота (в метрах). Пользуясь этой формулой, найдите
высоту ![]() , если основания трапеции равны
, если основания трапеции равны ![]() и
и ![]() , а её площадь
, а её площадь ![]() .
.
5. Задание 13 № 311535Радиус вписанной в прямоугольный треугольник окружности
можно найти по формуле ![]() , где
, где ![]() и
и ![]() — катеты, а
— катеты, а ![]() — гипотенуза треугольника. Пользуясь этой
формулой, найдите
— гипотенуза треугольника. Пользуясь этой
формулой, найдите ![]() , если
, если ![]() и
и ![]() .
.
6. Задание 13 № 311541Объём пирамиды вычисляют по формуле ![]() , где
, где ![]() — площадь основания пирамиды,
— площадь основания пирамиды, ![]() — её высота. Объём пирамиды равен 40, площадь
основания 15. Чему равна высота пирамиды?
— её высота. Объём пирамиды равен 40, площадь
основания 15. Чему равна высота пирамиды?
7. Задание 13 № 311543Площадь любого выпуклого четырехугольника можно
вычислять по формуле ![]() , где
, где ![]() — длины его диагоналей, а
— длины его диагоналей, а ![]() угол между ними. Вычислите
угол между ними. Вычислите ![]() , если
, если ![]() .
.
8. Задание 13 № 311824Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.
9. Задание 13 № 311920Центростремительное ускорение при движении по окружности
(в м/c2 ) можно вычислить по формуле ![]() где
где ![]() — угловая скорость (в с−1),
а R — радиус окружности. Пользуясь этой формулой, найдите
расстояние R (в метрах), если угловая скорость равна 3 с−1,
а центростремительное ускорение равно 45 м/c2.
— угловая скорость (в с−1),
а R — радиус окружности. Пользуясь этой формулой, найдите
расстояние R (в метрах), если угловая скорость равна 3 с−1,
а центростремительное ускорение равно 45 м/c2.
10. Задание 13 № 311964Из закона всемирного тяготения ![]() выразите массу
выразите массу ![]() и найдите её величину (в килограммах),
если
и найдите её величину (в килограммах),
если ![]()
![]()
![]() и гравитационная постоянная
и гравитационная постоянная ![]()
11. Задание 13 № 316355Полную механическую энергию тела (в джоулях) можно вычислить
по формуле ![]() где
где ![]() — масса тела (в килограммах),
— масса тела (в килограммах), ![]() — его скорость (в м/с),
— его скорость (в м/с), ![]() — высота положения центра масс тела над произвольно
выбранным нулевым уровнем (в метрах), а
— высота положения центра масс тела над произвольно
выбранным нулевым уровнем (в метрах), а ![]() — ускорение свободного падения (в м/с2).
Пользуясь этой формулой, найдите
— ускорение свободного падения (в м/с2).
Пользуясь этой формулой, найдите ![]() (в метрах), если
(в метрах), если ![]()
![]()
![]() а
а ![]()
12. Задание 13 № 316914Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 150 ватт, а сила тока равна 5 амперам.
13. Задание 13 № 318530Закон Кулона можно записать в виде ![]() где
где ![]() — сила взаимодействия зарядов (в ньютонах),
— сила взаимодействия зарядов (в ньютонах), ![]() и
и ![]() — величины зарядов (в кулонах),
— величины зарядов (в кулонах), ![]() — коэффициент пропорциональности (в Н·м2/Кл2 ),
а
— коэффициент пропорциональности (в Н·м2/Кл2 ),
а ![]() — расстояние между зарядами (в метрах). Пользуясь
формулой, найдите величину заряда
— расстояние между зарядами (в метрах). Пользуясь
формулой, найдите величину заряда ![]() (в кулонах), если
(в кулонах), если ![]() Н·м2/Кл2,
Н·м2/Кл2, ![]() Кл,
Кл, ![]() м, а
м, а ![]() Н.
Н.
14. Задание 13 № 338056Закон всемирного тяготения можно записать в
виде ![]() где
где ![]() — сила притяжения между телами (в ньютонах),
— сила притяжения между телами (в ньютонах), ![]() и
и ![]() — массы тел (в килограммах),
— массы тел (в килограммах), ![]() — расстояние между центрами масс (в метрах),
а
— расстояние между центрами масс (в метрах),
а ![]() — гравитационная постоянная, равная
6.67 · 10−11 H·м2/кг2.
Пользуясь формулой, найдите массу тела
— гравитационная постоянная, равная
6.67 · 10−11 H·м2/кг2.
Пользуясь формулой, найдите массу тела ![]() (в килограммах), если
(в килограммах), если ![]() Н,
Н, ![]() кг, а
кг, а ![]() м.
м.
15. Задание 13 № 338089Закон Джоуля–Ленца можно записать в виде Q = I2Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q = 2187 Дж, I = 9 A, R = 3 Ом.
16. Задание 13 № 338238Площадь четырёхугольника можно вычислить по формуле ![]() где
где ![]() и
и ![]() — длины диагоналей четырёхугольника,
— длины диагоналей четырёхугольника, ![]() — угол между диагоналями. Пользуясь этой формулой,
найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой,
найдите длину диагонали ![]() если
если ![]()
![]() a
a ![]()
17. Задание 13 № 338296Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м3.
Разные задачи
1. Задание 13 № 46Период колебания математического маятника ![]() (в секундах) приближенно можно вычислить по формуле
(в секундах) приближенно можно вычислить по формуле ![]() , где
, где ![]() — длина нити (в метрах). Пользуясь этой формулой,
найдите длину нити маятника (в метрах), период колебаний которого
составляет 3 секунды.
— длина нити (в метрах). Пользуясь этой формулой,
найдите длину нити маятника (в метрах), период колебаний которого
составляет 3 секунды.
2. Задание 13 № 311534Радиус описанной около треугольника окружности можно
найти по формуле ![]() , где
, где ![]() — сторона треугольника,
— сторона треугольника, ![]() — противолежащий этой стороне угол, а
— противолежащий этой стороне угол, а ![]() — радиус описанной около этого треугольника
окружности. Пользуясь этой формулой, найдите
— радиус описанной около этого треугольника
окружности. Пользуясь этой формулой, найдите ![]() , если
, если ![]() , а
, а ![]() .
.
3. Задание 13 № 311536Длину биссектрисы треугольника, проведённой к стороне
![]() , можно вычислить по формуле
, можно вычислить по формуле ![]() . Вычислите
. Вычислите ![]() , если
, если ![]() .
.
4. Задание 13 № 318356За 20 минут велосипедист проехал 7 километров. Сколько километров он проедет за t минут, если будет ехать с той же скоростью? Запишите соответствующее выражение.
Линейные неравенства
1. Задание 14 № 311417 Решите неравенство
![]() .
.
В ответе укажите номер правильного варианта.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Задание 14 № 314557Решите неравенство ![]()
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
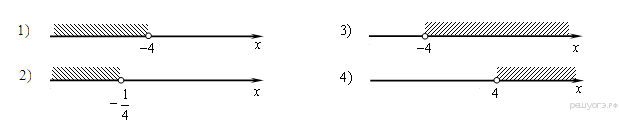
3. Задание 14 № 314567Решите неравенство ![]() и определите, на каком рисунке изображено множество
его решений.
и определите, на каком рисунке изображено множество
его решений.
В ответе укажите номер правильного варианта.

4. Задание 14 № 314580 Решите
неравенство ![]() и определите, на каком рисунке изображено множество
его решений.
и определите, на каком рисунке изображено множество
его решений.
В ответе укажите номер правильного варианта.
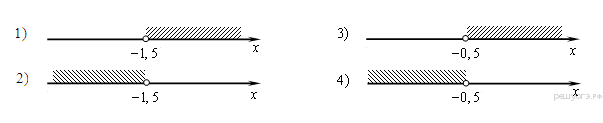
5. Задание 14 № 314581 Решите
неравенство ![]() и определите, на каком рисунке изображено множество
его решений.
и определите, на каком рисунке изображено множество
его решений.
В ответе укажите номер правильного варианта.
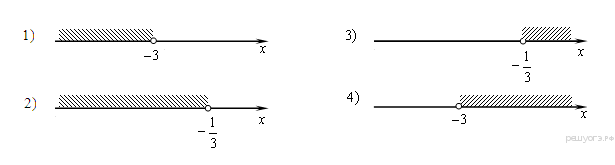
6. Задание 14 № 319930 При каких значениях a выражение 5a + 9 принимает отрицательные значения?В ответе укажите номер правильного варианта.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7. Задание 14 № 338481Решите неравенство ![]()
1) (−4; +∞) 2) (−12; +∞) 3) (−∞; −4) 4) (−∞; −12)
8. Задание 14 № 338490 При каких значениях x значение выражения 9x + 7 меньше значения выражения 8x − 3?
1) x > 4 2) x < 4 3) x > − 10 4) x < − 10
9. Задание 14 № 338590 Решите
неравенство ![]()
1) (− ∞; 8) 2) (− ∞; 1) 3) (8; +∞) 4) (1; +∞)
10. Задание 14 № 338677 При
каких значениях x значение выражения ![]() больше значения выражения
больше значения выражения ![]() ?
?
1) x > − 10 2) x < − 10 3) x > − 6 4) x < − 6
11. Задание 14 № 338695 Решите
неравенство ![]()
1) [−0,4; +∞) 2) (−∞; −2] 3) [−2; +∞) 4) (−∞; −0,4]
12. Задание 14 № 339292На каком рисунке изображено множество решений неравенства ![]()
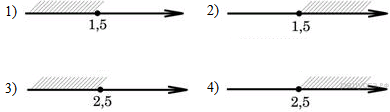
13. Задание 14 № 341213На каком рисунке изображено множество решений неравенства ![]()
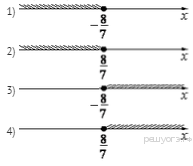
Квадратные неравенства
1. Задание 14 № 81 На каком рисунке
изображено множество решений неравенства ![]()
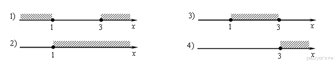
2. Задание 14 № 185Решение какого из данных неравенств изображено на
рисунке![]() 1)
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3. Задание 14 № 311309 Решите
неравенство ![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4. Задание 14 № 311310 Решите
неравенство ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5. Задание 14 № 311311Решите неравенство ![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6. Задание 14 № 311312 Решите
неравенство ![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7. Задание 14 № 311349 Решите
неравенство ![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Задание 14 № 311385 На
каком рисунке изображено множество решений неравенства ![]() ?
?
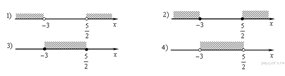 1) 1 2) 2 3) 3 4) 4
1) 1 2) 2 3) 3 4) 4
9. Задание 14 № 311751Решите неравенство ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
10. Задание 14 № 314504На каком рисунке изображено множество решений неравенства ![]() ?
?
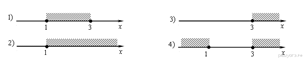
11. Задание 14 № 314579На каком рисунке изображено множество решений неравенства ![]() ?
?
![]()
12. Задание 14 № 314587На каком рисунке изображено множество решений неравенства ![]() ?
?
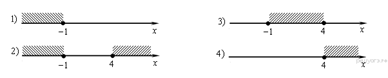
13. Задание 14 № 314596Решение какого из данных неравенств изображено на рисунке?
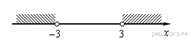 1)
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
14. Задание 14 № 314602На каком рисунке изображено множество решений неравенства ![]() ?
? 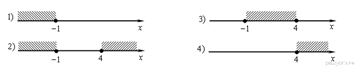
15. Задание 14 № 314604![]() Решение какого из данных неравенств изображено на
рисунке?
Решение какого из данных неравенств изображено на
рисунке?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
16. Задание 14 № 314610![]() Решение какого из данных неавенств изображено на
рисунке?
Решение какого из данных неавенств изображено на
рисунке?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
17. Задание 14 № 316222 Решите
неравенство: ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
18. Задание 14 № 316275 Решите
неравенство: ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
19. Задание 14 № 316312 Решите
неравенство: ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
20. Задание 14 № 320664 Укажите неравенство, которое не имеет решений.
1) x2 − 64 ≤ 0 2) x2 + 64 ≥ 0 3) x2 − 64 ≥ 0 4) x2 + 64 ≤ 0
21. Задание 14 № 320666 Укажите неравенство, решением которого является любое число.
1) x2 − 15 < 0 2) x2 + 15 > 0 3) x2 + 15 < 0 4) x2 − 15 > 0
22. Задание 14 № 333004 Решение какого из данных неравенств изображено на рисунке?
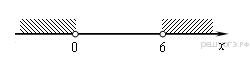 1)
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
23. Задание 14 № 338497 На
каком из рисунков изображено решение неравенства ![]()
 1) 1 2) 2 3) 3 4) 4
1) 1 2) 2 3) 3 4) 4
24. Задание 14 № 338499 Решите
неравенство ![]()
1) (− ∞; +∞) 2) (− ∞; −6)∪(6; +∞) 3) (− 6; 6) 4) нет решений
25. Задание 14 № 338513 На
каком рисунке изображено множество решений неравенства ![]()
![]()
1) 1 2) 2 3) 3 4) 4
26. Задание 14 № 338523 На
каком из рисунков изображено решение неравенства ![]()
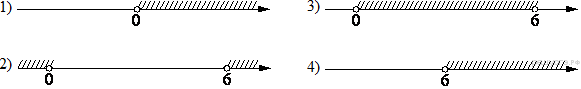
1) 1 2) 2 3) 3 4) 4
27. Задание 14 № 338550 Решите
неравенство ![]()
1) (− ∞; +∞) 2) нет решений 3) (− 5; 5) 4) (− ∞; −5)∪(5; +∞)
28. Задание 14 № 338599 На
каком рисунке изображено решение неравенства ![]()
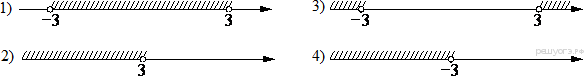
1) 1 2) 2 3) 3 4) 4
29. Задание 14 № 338745 На
каком из рисунков изображено решение неравенства ![]()
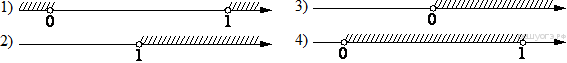
1) 1 2) 2 3) 3 4) 4
30. Задание 14 № 338762 На
каком из рисунков изображено решение неравенства ![]()
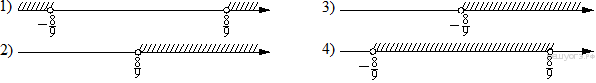
1) 1 2) 2 3) 3 4) 4
31. Задание 14 № 349127На каком рисунке изображено множество решений
неравенства ![]() ?
?
![]()
32. Задание 14 № 349136На каком рисунке изображено множество решений
неравенства ![]() ?
?
![]()
33. Задание 14 № 349364На каком рисунке изображено множество решений
неравенства ![]() ?
?
![]()
34. Задание 14 № 349408На каком рисунке изображено множество решений
неравенства ![]() ?
?
![]()
35. Задание 14 № 349529На каком рисунке изображено множество решений
неравенства ![]() ?
?
![]()
36. Задание 14 № 349532На каком рисунке изображено множество решений
неравенства ![]() ?
?
![]()
37. Задание 14 № 349715На каком рисунке изображено множество решений
неравенства ![]() ?
?
![]()
38. Задание 14 № 350079На каком рисунке изображено множество решений
неравенства ![]() ?
?

Системы неравенств
1. Задание 14 № 311672Решите систему неравенств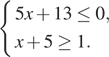
На каком рисунке изображено множество её решений?.
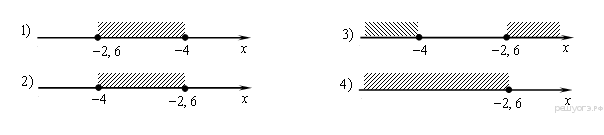
2. Задание 14 № 311949Решите систему неравенств 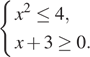
На каком из рисунков изображено множество её решений?
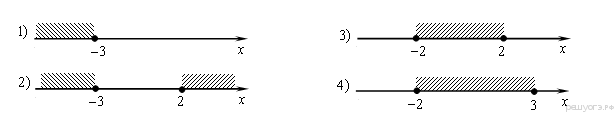
3. Задание 14 № 314490Найдите наибольшее значение ![]() , удовлетворяющее системе неравенств
, удовлетворяющее системе неравенств 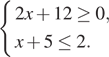
4. Задание 14 № 333109Решите систему неравенств 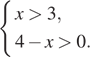
На каком рисунке изображено множество её решений?
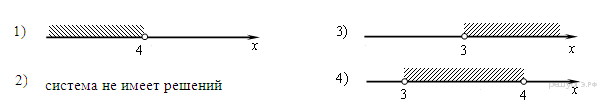
5. Задание 14 № 341322На каком рисунке изображено множество решений системы неравенств
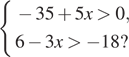
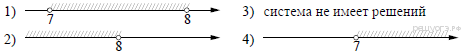
6. Задание 14 № 348461Укажите решение системы неравенств: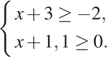

7. Задание 14 № 348486Укажите решение системы неравенств: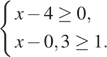
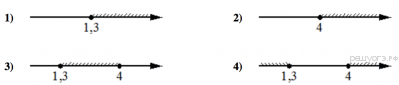
Углы
1. Задание 15 № 132756 Колесо имеет 18 спиц. Углы между соседними спицами равны.
Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.
Колесо имеет 18 спиц. Углы между соседними спицами равны.
Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.
2. Задание 15 № 132757Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 18°?
3. Задание 15 № 132758Какой угол (в градусах) образуют минутная и часовая стрелки часов в 5 ч?
4. Задание 15 № 132759Какой угол (в градусах) описывает минутная стрелка за 10 мин?
5. Задание 15 № 132761На какой угол (в градусах) поворачивается минутная
стрелка пока часовая проходит ![]() ?
?
6. Задание 15 № 324986Сколько спиц в колесе, если угол между соседними спицами равен 8°?
7. Задание 15 № 325073На сколько градусов повернется Земля вокруг своей оси за 7 часов?
8. Задание 15 № 325085За сколько часов Земля повернется вокруг своей оси на 120°?
9. Задание 15 № 341336 На рисунке показано, как выглядит колесо с 7 спицами.
Найдите величину угла (в градусах), который образуют две сосе
На рисунке показано, как выглядит колесо с 7 спицами.
Найдите величину угла (в градусах), который образуют две сосе
Теорема Пифагора
1. Задание 15 № 70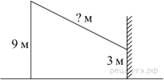 От столба высотой 9 м к дому натянут провод, который
крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до
столба 8 м. Вычислите длину провода.
От столба высотой 9 м к дому натянут провод, который
крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до
столба 8 м. Вычислите длину провода.
2. Задание 15 № 96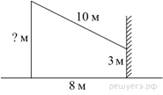 От столба к дому натянут провод длиной 10 м, который
закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите
высоту столба, если расстояние от дома до столба равно 8 м.
От столба к дому натянут провод длиной 10 м, который
закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите
высоту столба, если расстояние от дома до столба равно 8 м.
3. Задание 15 № 148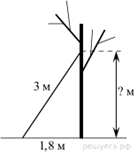 Лестницу длиной 3 м прислонили к дереву. На какой высоте
(в метрах) находится верхний её конец, если нижний конец отстоит от ствола
дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте
(в метрах) находится верхний её конец, если нижний конец отстоит от ствола
дерева на 1,8 м?
4. Задание 15 № 13275 Мальчик прошел от дома по направлению на восток 800 м.
Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от
дома оказался мальчик?
Мальчик прошел от дома по направлению на восток 800 м.
Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от
дома оказался мальчик?
5. Задание 15 № 132752 Девочка прошла от дома по направлению на запад 500 м.
Затем повернула на север и прошла 300 м. После этого она повернула на восток
и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась
девочка?
Девочка прошла от дома по направлению на запад 500 м.
Затем повернула на север и прошла 300 м. После этого она повернула на восток
и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась
девочка?
6. Задание 15 № 132753Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка — 3 км/ч. Какое расстояние (в километрах) будет между ними через 30 минут?
7. Задание 15 № 311509Глубина крепостного рва равна 8 м, ширина 5 м, а высота
крепостной стены от ее основания 20 м. Длина лестницы, по которой можно
взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней
точки стены (см. рис.). Найдите длину лестницы.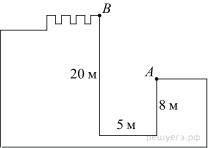
8. Задание 15 № 311854Девочка прошла от дома по направлению на запад 20 м. Затем повернула на север и прошла 800 м. После этого она повернула на восток и прошла ещё 200 м. На каком расстоянии (в метрах) от дома оказалась девочка?
9. Задание 15 № 311962Лестница соединяет точки A и B и состоит из 35 ступеней. Высота каждой ступени равна 14 см, а длина — 48 см. Найдите расстояние между точками A и B (в метрах).
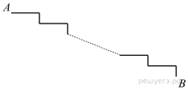
10. Задание 15 № 31484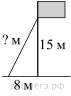 Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 15 м от земли. Расстояние от основания
флагштока до места крепления троса на земле равно 8 м. Найдите длину
троса.
Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 15 м от земли. Расстояние от основания
флагштока до места крепления троса на земле равно 8 м. Найдите длину
троса.
11. Задание 15 № 315106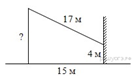 От столба к дому натянут провод длиной 17 м, который
закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите
высоту столба, если расстояние от дома до столба равно 15 м.
От столба к дому натянут провод длиной 17 м, который
закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите
высоту столба, если расстояние от дома до столба равно 15 м.
12. Задание 15 № 31628Девочка прошла от дома по направлению на запад 880 м. Затем повернула на север и прошла 900 м. После этого она повернула на восток и прошла ещё 400 м. На каком расстоянии (в метрах) от дома оказалась девочка?
13. Задание 15 № 31632Мальчик прошёл от дома по направлению на восток 400 м. Затем повернул на север и прошёл 90 м. На каком расстоянии (в метрах) от дома оказался мальчик?
14. Задание 15 № 31635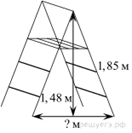 Длина стремянки в сложенном виде равна 1,85 м, а её высота
в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах)
между основаниями стремянки в разложенном виде.
Длина стремянки в сложенном виде равна 1,85 м, а её высота
в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах)
между основаниями стремянки в разложенном виде.
15. Задание 15 № 316378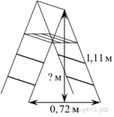 Длина тремянки в сложенном виде равна 1,11 м, а расстояние
между её основаниями в разложенном виде составляет 0,72 м. Найдите
высоту (в метрах) стремянки в разложенном виде.
Длина тремянки в сложенном виде равна 1,11 м, а расстояние
между её основаниями в разложенном виде составляет 0,72 м. Найдите
высоту (в метрах) стремянки в разложенном виде.
16. Задание 15 № 322886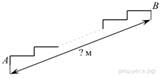 Лестница соединяет точки A и B и
состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а
длина — 28 см. Найдите расстояние между точками A и B(в
метрах).
Лестница соединяет точки A и B и
состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а
длина — 28 см. Найдите расстояние между точками A и B(в
метрах).
17. Задание 15 № 324941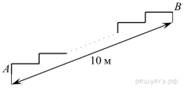 Лестница соединяет точки A и B . Высота каждой ступени
равна 14 см, а длина — 48 см. Расстояние между точками A и B составляет
10 м. Найдите высоту, на которую поднимается лестница (в метрах).
Лестница соединяет точки A и B . Высота каждой ступени
равна 14 см, а длина — 48 см. Расстояние между точками A и B составляет
10 м. Найдите высоту, на которую поднимается лестница (в метрах).
18. Задание 15 № 3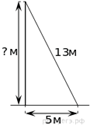 Пожарную лестницу длиной 13 м приставили к окну пятого
этажа дома. Нижний конец лестницы отстоит от стены на 5 м. На какой высоте
расположено окно? Ответ дайте в метрах
Пожарную лестницу длиной 13 м приставили к окну пятого
этажа дома. Нижний конец лестницы отстоит от стены на 5 м. На какой высоте
расположено окно? Ответ дайте в метрах
19. Задание 15 № 32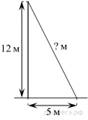 Пожарную лестницу приставили к окну, расположенному на
высоте 12 м
Пожарную лестницу приставили к окну, расположенному на
высоте 12 м
от земли. Нижний конец лестницы отстоит от стены на 5 м. Какова длина лестницы? Ответ дайте в метрах.
20. Задание 15 № 3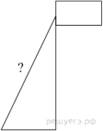 Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 5,5 м от земли. Расстояние от основания
флагштока до места крепления троса на земле равно 4,8 м. Найдите длину
троса. Ответ дайте в метрах.
Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 5,5 м от земли. Расстояние от основания
флагштока до места крепления троса на земле равно 4,8 м. Найдите длину
троса. Ответ дайте в метрах.
21. Задание 15 № 3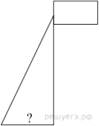 Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 6,3 м от земли. Длина троса равна 6,5 м.
Найдите расстояние от точки основания флагштока до места крепления
троса на земле. Ответ дайте в метрах.
Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 6,3 м от земли. Длина троса равна 6,5 м.
Найдите расстояние от точки основания флагштока до места крепления
троса на земле. Ответ дайте в метрах.
22. Задание 15 № 32528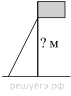 Расстояние от основания флагштока до места крепления
троса на земле равно 1,6 м. Длина троса равна 3,4 м. Найдите расстояние от
земли до точки крепления троса, удерживающего флагшток в вертикальном
положении. Ответ дайте в метрах.
Расстояние от основания флагштока до места крепления
троса на земле равно 1,6 м. Длина троса равна 3,4 м. Найдите расстояние от
земли до точки крепления троса, удерживающего флагшток в вертикальном
положении. Ответ дайте в метрах.
23. Задание 15 № 33312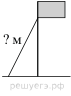 Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 6,3 м от земли. Расстояние от основания
флагштока до места крепления троса на земле равно 1,6 м. Найдите длину
троса в метрах.
Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 6,3 м от земли. Расстояние от основания
флагштока до места крепления троса на земле равно 1,6 м. Найдите длину
троса в метрах.
24. Задание 15 № 333150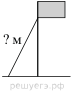 Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 4,4 м от земли. Расстояние от основания
флагштока до места крепления троса на земле равно 3,3 м. Найдите длину
троса в метрах.
Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 4,4 м от земли. Расстояние от основания
флагштока до места крепления троса на земле равно 3,3 м. Найдите длину
троса в метрах.
25. Задание 15 № 341503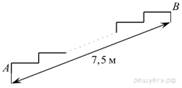 Лестница соединяет точки A и B. Высота каждой ступени
равна 10,5 см, а длина равна 36 см. Расстояние между точками A и B составляет
7,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Лестница соединяет точки A и B. Высота каждой ступени
равна 10,5 см, а длина равна 36 см. Расстояние между точками A и B составляет
7,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
26. Задание 15 № 341529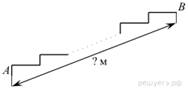 Лестница соединяет точки A и B и состоит из 30
ступеней. Высота каждой ступени равна 16 см, а длина равна 63 см. Найдите
расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 30
ступеней. Высота каждой ступени равна 16 см, а длина равна 63 см. Найдите
расстояние между точками A и B (в метрах).
Подобие треугольников
1. Задание 15 № 44Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
2. Задание 15 № 132764Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?
3. Задание 15 № 132765Человек ростом 1,8 м стоит на расстоянии 12 м от столба, на котором висит фонарь на высоте 5,4 м. Найдите длину тени человека в метрах.
4. Задание 15 № 311513Короткое плечо шлагбаума имеет длину 1 м, а длинное
плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча,
когда конец длинного плеча поднимается на 1,8 м?
5. Задание 15 № 311516 Короткое плечо шлагбаума имеет длину 1 м, а длинное
плечо – 4 м. На какую высоту (в метрах) поднимается конец длинного
плеча, когда конец короткого опускается на 0,5 м?
Короткое плечо шлагбаума имеет длину 1 м, а длинное
плечо – 4 м. На какую высоту (в метрах) поднимается конец длинного
плеча, когда конец короткого опускается на 0,5 м?
6. Задание 15 № 314820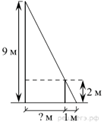 На каком расстоянии (в метрах) от фонаря стоит человек
ростом 2 м, если длина его тени равна 1 м, высота фонаря 9
м?
На каком расстоянии (в метрах) от фонаря стоит человек
ростом 2 м, если длина его тени равна 1 м, высота фонаря 9
м?
7. Задание 15 № 314914Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).
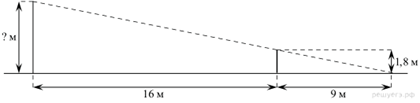
8. Задание 15 № 322903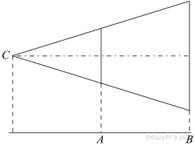 Проектор полностью освещает экран A высотой
80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем
расстоянии (в сантиметрах) от проектора нужно расположить
экран B высотой 330 см, чтобы он был полностью освещён,
если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой
80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем
расстоянии (в сантиметрах) от проектора нужно расположить
экран B высотой 330 см, чтобы он был полностью освещён,
если настройки проектора остаются неизменными?
Вычисление длин и площадей
1. Задание 15 № 132766Площадь прямоугольного земельного участка равна 9 га, ширина участка равна 150 м. Найдите длину этого участка в метрах.
2. Задание 15 № 132767Найдите периметр прямоугольного участка земли, площадь которого равна 800 м2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.
3. Задание 15 № 132772Сколько досок длиной 3,5 м, шириной 20 см и толщиной
20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении
прямоугольник размером 30 см ![]() 40 см?
40 см?
4. Задание 15 № 311323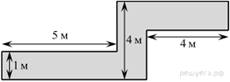 Определите, сколько необходимо закупить пленки
Определите, сколько необходимо закупить пленки ![]() для гидроизоляции садовой дорожки, изображенной
на рисунке, если её ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной
на рисунке, если её ширина везде одинакова.
5. Задание 15 № 311358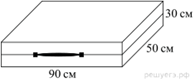 Дизайнер Павел получил заказ на декорирование чемодана
цветной бумагой. По рисунку определите, сколько бумаги (в см2)
необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность
чемодана, если каждую грань он будет обклеивать отдельно (без загибов).
Дизайнер Павел получил заказ на декорирование чемодана
цветной бумагой. По рисунку определите, сколько бумаги (в см2)
необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность
чемодана, если каждую грань он будет обклеивать отдельно (без загибов).
6. Задание 15 № 311378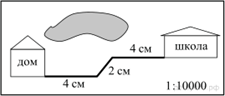 На карте показан путь Лены от дома до школы. Лена измерила
длину каждого участка и подписала его. Используя рисунок, определите,
длину пути (в м), если масштаб 1 см: 10000 см.
На карте показан путь Лены от дома до школы. Лена измерила
длину каждого участка и подписала его. Используя рисунок, определите,
длину пути (в м), если масштаб 1 см: 10000 см.
7. Задание 15 № 311502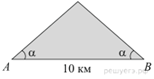 Склоны горы образуют с горизонтом угол
Склоны горы образуют с горизонтом угол ![]() , косинус которого равен 0,8. Расстояние по карте
между точками A и B равно 10 км. Определите
длину пути между этими точками через вершину горы.
, косинус которого равен 0,8. Расстояние по карте
между точками A и B равно 10 км. Определите
длину пути между этими точками через вершину горы.
8. Задание 15 № 311918Глубина бассейна составляет 2 метра, ширина — 10 метров, а длина — 25 метров. Найдите суммарную площадь боковых стен и дна бассейна (в квадратных метрах).
9. Задание 15 № 325137Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
10. Задание 15 № 325147Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 4,4 м?
11. Задание 15 № 325157Две трубы, диаметры которых равны 7 см и 24 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
12. Задание 15 № 325197Сколько досок длиной 4 м, шириной 20 см и толщиной 30 мм выйдет из бруса длиной 80 дм, имеющего в сечении прямоугольник размером 30 см × 40 см?
13. Задание 15 № 325244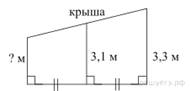 Наклонная крыша установлена на трёх вертикальных
опорах, расположенных на одной прямой. Средняя опора стоит посередине
между малой и большой опорами (см. рис.). Высота средней опоры 3,1 м, высота
большей опоры 3,3 м. Найдите высоту малой опоры.
Наклонная крыша установлена на трёх вертикальных
опорах, расположенных на одной прямой. Средняя опора стоит посередине
между малой и большой опорами (см. рис.). Высота средней опоры 3,1 м, высота
большей опоры 3,3 м. Найдите высоту малой опоры.
14. Задание 15 № 340269 Картинка имеет форму прямоугольника со сторонами
19 см и 32 см. Её наклеили на белую бумагу так, что вокруг
картинки получилась белая окантовка одинаковой ширины. Площадь, которую
занимает картинка с окантовкой, равна 1080 см2. Какова
ширина окантовки? Ответ дайте в сантиметрах.
Картинка имеет форму прямоугольника со сторонами
19 см и 32 см. Её наклеили на белую бумагу так, что вокруг
картинки получилась белая окантовка одинаковой ширины. Площадь, которую
занимает картинка с окантовкой, равна 1080 см2. Какова
ширина окантовки? Ответ дайте в сантиметрах.
15. Задание 15 № 340291Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 30×50×90 (см) можно поместить в кузов машины размером 2,4×3×2,7 (м)?
16. Задание 15 № 348436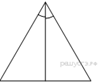 Сторона равностороннего треугольника равна
Сторона равностороннего треугольника равна ![]() . Найдите биссектрису этого треугольника.
. Найдите биссектрису этого треугольника.
17. Задание 15 № 348684 Картинка имеет форму прямоугольника со сторонами 11 см и 13
см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая
окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой,
равна 675 см
Картинка имеет форму прямоугольника со сторонами 11 см и 13
см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая
окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой,
равна 675 см![]() . Какова ширина окантовки? Ответ дайте в сантиметрах.
. Какова ширина окантовки? Ответ дайте в сантиметрах.
18. Задание 15 № 348686 Картинка имеет форму прямоугольника со сторонами 12 см и 32
см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая
окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой,
равна 684 см
Картинка имеет форму прямоугольника со сторонами 12 см и 32
см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая
окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой,
равна 684 см![]() . Какова ширина окантовки? Ответ дайте в сантиметрах.
. Какова ширина окантовки? Ответ дайте в сантиметрах.
19. Задание 15 № 34877
Картинка имеет
форму прямоугольника со сторонами 14 см и 27 см. Её наклеили на белую бумагу так,
что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь,
которую занимает картинка с окантовкой, равна 558 см![]() .
Какова ширина окантовки? Ответ дайте в сантиметрах.
.
Какова ширина окантовки? Ответ дайте в сантиметрах.
20. Задание 15 № 350056 Картинка имеет форму прямоугольника со сторонами
24 см и 38 см. Её наклеили на белую бумагу так, что вокруг
картинки получилась белая окантовка одинаковой ширины. Площадь, которую
занимает картинка с окантовкой, равна 1976 см2. Какова
ширина окантовки? Ответ дайте в сантиметрах.
Картинка имеет форму прямоугольника со сторонами
24 см и 38 см. Её наклеили на белую бумагу так, что вокруг
картинки получилась белая окантовка одинаковой ширины. Площадь, которую
занимает картинка с окантовкой, равна 1976 см2. Какова
ширина окантовки? Ответ дайте в сантиметрах.
21. Задание 15 № 353477Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 40×80×100 (см) можно поместить в кузов машины размером 3,2×3,2×8 (м)?
Разные задачи
1. Задание 15 № 132754Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 15 км/ч и 20 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?
2. Задание 15 № 132755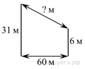 В 60 м одна от другой растут две сосны. Высота одной 31
м, а другой — 6 м. Найдите расстояние (в метрах) между их верхушками.
В 60 м одна от другой растут две сосны. Высота одной 31
м, а другой — 6 м. Найдите расстояние (в метрах) между их верхушками.
3. Задание 15 № 311335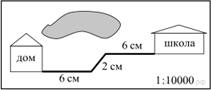 На карте показан путь Лены от дома до школы. Лена измерила
длину каждого участка и подписала его. Используя рисунок, определите
длину пути (в м), если масштаб 1 см : 10 000 см.
На карте показан путь Лены от дома до школы. Лена измерила
длину каждого участка и подписала его. Используя рисунок, определите
длину пути (в м), если масштаб 1 см : 10 000 см.
4. Задание 15 № 311414 Сколько всего осей симметрии имеет фигура, изображённая
на рисунке?
Сколько всего осей симметрии имеет фигура, изображённая
на рисунке?
5. Задание 15 № 311519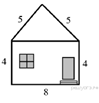 Определите высоту дома, ширина фасада которого
равна 8 м, высота от фундамента до крыши равна 4 м, а длина ската крыши
равна 5 м.
Определите высоту дома, ширина фасада которого
равна 8 м, высота от фундамента до крыши равна 4 м, а длина ската крыши
равна 5 м.
6. Задание 15 № 311524Лестница соединяет точки ![]() и
и ![]() , расстояние между которыми равно 25 м. Высота
каждой ступени равна 14 см, а длина — 48 см. Найдите высоту
, расстояние между которыми равно 25 м. Высота
каждой ступени равна 14 см, а длина — 48 см. Найдите высоту ![]() (в метрах), на которую поднимается лестница.
(в метрах), на которую поднимается лестница.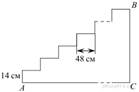
7. Задание 15 № 311526Обхват ствола секвойи равен 4,8 м. Чему равен его диаметр
(в метрах)? Ответ округлите до десятых.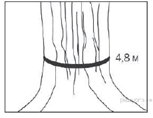
8. Задание 15 № 324943 Наклонная крыша установлена на трёх вертикальных
опорах, расположенных на одной прямой. Средняя опора стоит посередине
между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота
большой опоры 2,8 м. Найдите высоту средней опоры.
Наклонная крыша установлена на трёх вертикальных
опорах, расположенных на одной прямой. Средняя опора стоит посередине
между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота
большой опоры 2,8 м. Найдите высоту средней опоры.
Углы
1. Задание 16 № 3113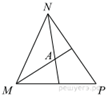 Биссектрисы углов N и M треугольника
MNP пересекаются в точке A. Найдите
Биссектрисы углов N и M треугольника
MNP пересекаются в точке A. Найдите
![]() , если
, если ![]() , а
, а ![]()
2. Задание 16 № 31141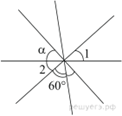 Углы, отмеченные на рисунке одной дугой, равны. Найдите
угол α. Ответ дайте в градусах.
Углы, отмеченные на рисунке одной дугой, равны. Найдите
угол α. Ответ дайте в градусах.
3. Задание 16 № 3114 Углы, отмеченные на рисунке одной дугой, равны. Найдите
угол
Углы, отмеченные на рисунке одной дугой, равны. Найдите
угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
4. Задание 16 № 3115 На плоскости даны четыре прямые. Известно, что
На плоскости даны четыре прямые. Известно, что ![]() ,
, ![]() ,
, ![]() . Найдите
. Найдите ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
5. Задание 16 № 32353 Диагональ прямоугольника образует угол 51° с одной
из его сторон. Найдите острый угол между диагоналями этого прямоугольника.
Ответ дайте в градусах.
Диагональ прямоугольника образует угол 51° с одной
из его сторон. Найдите острый угол между диагоналями этого прямоугольника.
Ответ дайте в градусах.
6. Задание 16 № 33937 Прямые m и n параллельны.
Найдите ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в градусах.
Прямые m и n параллельны.
Найдите ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в градусах.
7. Задание 16 № 33 Найдите величину угла DOK, если OK —
биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.
Найдите величину угла DOK, если OK —
биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.
8. Задание 16 № 33 Найдите величину угла AOK, если OK —
биссектриса угла AOD, ∠DOB = 64°. Ответ дайте в градусах.
Найдите величину угла AOK, если OK —
биссектриса угла AOD, ∠DOB = 64°. Ответ дайте в градусах.
9. Задание 16 № 34 На прямой AB взята точка M.
Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 60°.
Найдите угол CMA. Ответ дайте в градусах.
На прямой AB взята точка M.
Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 60°.
Найдите угол CMA. Ответ дайте в градусах.
10. Задание 16 № 341330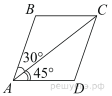 Диагональ AC параллелограмма ABCD образует
с его сторонами углы, равные 30° и 45° . Найдите больший угол
параллелограмма. Ответ дайте в градусах.
Диагональ AC параллелограмма ABCD образует
с его сторонами углы, равные 30° и 45° . Найдите больший угол
параллелограмма. Ответ дайте в градусах.
11. Задание 16 № 34861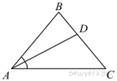 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() — биссектриса. Найдите угол
— биссектриса. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
12. Задание 16 № 34877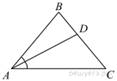 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() — биссектриса. Найдите угол
— биссектриса. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
13. Задание 16 № 348885В треугольнике два угла равны 54° и 58°. Найдите его третий угол. Ответ дайте в градусах.
14. Задание 16 № 34940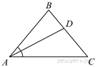 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() - биссектриса. Найдите угол
- биссектриса. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
15. Задание 16 № 349879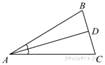 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() - биссектриса. Найдите угол
- биссектриса. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
16. Задание 16 № 3532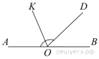 Найдите величину угла AOK, если OK —
биссектриса угла AOD, ∠DOB = 52°. Ответ дайте в градусах.
Найдите величину угла AOK, если OK —
биссектриса угла AOD, ∠DOB = 52°. Ответ дайте в градусах.
Треугольники общего вида
1. Задание 16 № 32307У треугольника со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
2. Задание 16 № 3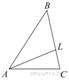 В треугольнике ABC проведена биссектриса AL, угол ALC равен
112°, угол ABC равен 106°. Найдите угол ACB. Ответ
дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен
112°, угол ABC равен 106°. Найдите угол ACB. Ответ
дайте в градусах.
3. Задание 16 № 339390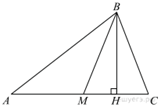 В треугольнике ABC проведены медиана BM и
высота BH . Известно, что AC = 84
и BC = BM. Найдите AH.
В треугольнике ABC проведены медиана BM и
высота BH . Известно, что AC = 84
и BC = BM. Найдите AH.
4. Задание 16 № 339 В остроугольном треугольнике
В остроугольном треугольнике ![]() высота
высота ![]() равна
равна ![]() а сторона
а сторона ![]() равна 40. Найдите
равна 40. Найдите ![]() .
.
5. Задание 16 № 339495 В треугольнике ABC AB = BC,
а высота AH делит сторону BC на отрезки BH = 64
и CH = 16. Найдите cosB.
В треугольнике ABC AB = BC,
а высота AH делит сторону BC на отрезки BH = 64
и CH = 16. Найдите cosB.
6. Задание 16 № 339544 В треугольнике ABC BM — медиана
и BH – высота. Известно, что AC = 216, HC = 54
и ∠ACB = 40°.
Найдите угол AMB. Ответ дайте в градусах.
В треугольнике ABC BM — медиана
и BH – высота. Известно, что AC = 216, HC = 54
и ∠ACB = 40°.
Найдите угол AMB. Ответ дайте в градусах.
7. Задание 16 № 339863Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
8. Задание 16 № 348399 Медиана равностороннего треугольника равна
Медиана равностороннего треугольника равна ![]() . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника.
9. Задание 16 № 349100 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() - медиана,
- медиана, ![]() . Найдите
. Найдите ![]() .
.
10. Задание 16 № 349189 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() - медиана,
- медиана, ![]() . Найдите
. Найдите ![]() .
.
11. Задание 16 № 349358В треугольнике два угла равны 36° и 73°. Найдите его третий угол. Ответ дайте в градусах.
12. Задание 16 № 349500В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.
13. Задание 16 № 349535![]() В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() - медиана,
- медиана, ![]() . Найдите
. Найдите ![]() .
.
14. Задание 16 № 349595 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() - медиана,
- медиана, ![]() . Найдите
. Найдите ![]() .
.
15. Задание 16 № 34969 Точки
Точки ![]() и
и ![]() являются серединами сторон
являются серединами сторон ![]() и
и ![]() треугольника
треугольника ![]() , сторона
, сторона ![]() равна 66, сторона
равна 66, сторона ![]() равна 37, сторона
равна 37, сторона ![]() равна 74. Найдите
равна 74. Найдите ![]()
16. Задание 16 № 349711![]() В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() - медиана,
- медиана, ![]() . Найдите
. Найдите ![]() .
.
17. Задание 16 № 349785В треугольнике два угла равны 38° и 89°. Найдите его третий угол. Ответ дайте в градусах.
18. Задание 16 № 349941В треугольнике два угла равны 31° и 94°. Найдите его третий угол. Ответ дайте в градусах.
Равнобедренные треугольники
1. Задание 16 № 3113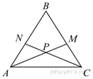 В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются
в точке P. Найдите
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются
в точке P. Найдите ![]() .
.
2. Задание 16 № 31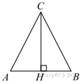 В равнобедренном треугольнике
В равнобедренном треугольнике ![]() . Найдите
. Найдите ![]() , если высота
, если высота ![]() .
.
3. Задание 16 № 31134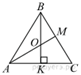 В равностороннем треугольнике ABC
медианы BK и AM пересекаются в
точке O. Найдите
В равностороннем треугольнике ABC
медианы BK и AM пересекаются в
точке O. Найдите ![]() .
.
4. Задание 16 № 31168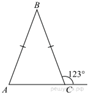 В равнобедренном треугольнике ABC с
основанием AC внешний угол при вершине C равен
123°. Найдите величину угла ABC. Ответ дайте в градусах.
В равнобедренном треугольнике ABC с
основанием AC внешний угол при вершине C равен
123°. Найдите величину угла ABC. Ответ дайте в градусах.
5. Задание 16 № 323376![]() Площадь равнобедренного треугольника равна
Площадь равнобедренного треугольника равна ![]() Угол, лежащий напротив основания равен 120°.
Найдите длину боковой стороны.
Угол, лежащий напротив основания равен 120°.
Найдите длину боковой стороны.
6. Задание 16 № 323416Периметр равнобедренного треугольника равен 196, а основание — 96. Найдите площадь треугольника.
7. Задание 16 № 339364 В треугольнике ABC AC = BC.
Внешний угол при вершине Bравен 146°. Найдите угол C.
Ответ дайте в градусах.
В треугольнике ABC AC = BC.
Внешний угол при вершине Bравен 146°. Найдите угол C.
Ответ дайте в градусах.
8. Задание 16 №Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.
9. Задание 16 №![]() Высота равностороннего треугольника равна
Высота равностороннего треугольника равна ![]() Найдите его периметр.
Найдите его периметр.
10. Задание 16 № 33945 В треугольнике ABC AB = BC = 53, AC = 56.
Найдите длину медианы BM.
В треугольнике ABC AB = BC = 53, AC = 56.
Найдите длину медианы BM.
11. Задание 16 № 341672 Боковая сторона равнобедренного треугольника
равна 10, а основание равно 12. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника
равна 10, а основание равно 12. Найдите площадь этого треугольника.
12. Задание 16 № 348593 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() . Найдите угол
. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
13. Задание 16 № 348764![]() В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() . Найдите угол
. Найдите угол![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
14. Задание 16 № 348![]() Сторона равностороннего треугольника равна
Сторона равностороннего треугольника равна ![]() . Найдите медиану этого треугольника.
. Найдите медиану этого треугольника.
15. Задание 16 № 34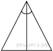 Сторона равностороннего треугольника равна
Сторона равностороннего треугольника равна ![]() . Найдите биссектрису этого треугольника.
. Найдите биссектрису этого треугольника.
16. Задание 16 № 3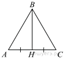 Сторона равностороннего треугольника равна
Сторона равностороннего треугольника равна ![]() . Найдите медиану этого треугольника.
. Найдите медиану этого треугольника.
17. Задание 16 № 349350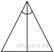 Биссектриса равностороннего треугольника равна
Биссектриса равностороннего треугольника равна ![]() . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника.
18. Задание 16 № 349374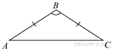 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() . Найдите угол
. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
19. Задание 16 № 349429![]() В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() . Найдите угол
. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
20. Задание 16 № 349471![]() Биссектриса равностороннего треугольника равна
Биссектриса равностороннего треугольника равна ![]() . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника.
21. Задание 16 № 349494![]() В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() . Найдите угол
. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
22. Задание 16 № 349524 Сторона равностороннего треугольника равна
Сторона равностороннего треугольника равна ![]() . Найдите высоту этого треугольника.
. Найдите высоту этого треугольника.
23. Задание 16 № 349645 Сторона равностороннего треугольника равна
Сторона равностороннего треугольника равна ![]() . Найдите медиану этого треугольника.
. Найдите медиану этого треугольника.
24. Задание 16 № 349671 Высота равностороннего треугольника равна
Высота равностороннего треугольника равна ![]() . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника.
25. Задание 16 № 349830 Биссектриса равностороннего треугольника равна
Биссектриса равностороннего треугольника равна ![]() . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника.
26. Задание 16 № 349955 Сторона равностороннего треугольника равна
Сторона равностороннего треугольника равна ![]() . Найдите биссектрису этого треугольника.
. Найдите биссектрису этого треугольника.
27. Задание 16 № 349965 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() . Найдите угол
. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
28. Задание 16 № 350010 Медиана равностороннего треугольника равна
Медиана равностороннего треугольника равна ![]() . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника.
29. Задание 16 № 353503 В треугольнике ABC AC = BC.
Внешний угол при вершине Bравен 140°. Найдите угол C.
Ответ дайте в градусах.
В треугольнике ABC AC = BC.
Внешний угол при вершине Bравен 140°. Найдите угол C.
Ответ дайте в градусах.
Прямоугольный треугольник
1. Задание 16 № 118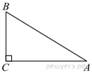 В треугольнике ABC угол C прямой, BC =
8 , sin A = 0,4. Найдите AB.
В треугольнике ABC угол C прямой, BC =
8 , sin A = 0,4. Найдите AB.
2. Задание 16 № 13277Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол. Ответ дайте в градусах.
3. Задание 16 № 311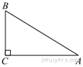 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() . Найдите
. Найдите ![]() .
.
4. Задание 16 № 311399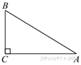 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() . Найдите
. Найдите ![]() .
.
5. Задание 16 № 311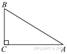 В треугольнике
В треугольнике ![]() угол
угол ![]() прямой,
прямой, ![]() . Найдите
. Найдите ![]() .
.
6. Задание 16 № 311500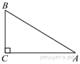 В треугольнике
В треугольнике ![]() угол
угол ![]() прямой,
прямой, ![]() . Найдите
. Найдите ![]() .
.
7. Задание 16 № 311760В треугольнике ABC угол C равен 90°, AC = 20, tgA = 0,5. Найдите BC.
8. Задание 16 № 311816В треугольнике ABC угол C равен
90°, BC = 20, ![]() = 0,5. Найдите AC.
= 0,5. Найдите AC.
9. Задание 16 № 316283В треугольнике ABC угол C равен 90°, BC = 12 , tgA = 1,5. Найдите AC.
10. Задание 16 № 316320В треугольнике ABC угол C равен 90°, AC = 12 , tgA = 1,5. Найдите BC.
11. Задание 16 № 322819Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведенную к гипотенузе.
12. Задание 16 № 322979![]() Катеты прямоугольного треугольника равны
Катеты прямоугольного треугольника равны ![]() и 1. Найдите синус наименьшего угла этого треугольника.
и 1. Найдите синус наименьшего угла этого треугольника.
13. Задание 16 № 323344![]() Площадь прямоугольного треугольника равна
Площадь прямоугольного треугольника равна ![]() Один из острых углов равен 30°. Найдите длину гипотенузы.
Один из острых углов равен 30°. Найдите длину гипотенузы.
14. Задание 16 №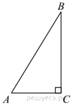 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]()
![]() Найдите
Найдите ![]()
15. Задание 16 № 339370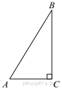 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]()
![]() Найдите
Найдите ![]()
16. Задание 16 № 339385![]() Площадь прямоугольного треугольника равна
Площадь прямоугольного треугольника равна ![]() Один из острых углов равен 30°. Найдите длину
катета, лежащего напротив этого угла.
Один из острых углов равен 30°. Найдите длину
катета, лежащего напротив этого угла.
17. Задание 16 № 339406![]() Площадь прямоугольного треугольника равна
Площадь прямоугольного треугольника равна ![]() Один из острых углов равен 30°. Найдите длину
катета, прилежащего к этому углу.
Один из острых углов равен 30°. Найдите длину
катета, прилежащего к этому углу.
18. Задание 16 № 339436Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABCк гипотенузе AC. Найдите AB, если AH = 6, AC = 24.
19. Задание 16 № 34000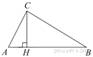 В прямоугольном треугольнике
В прямоугольном треугольнике ![]() катет
катет ![]() , а высота
, а высота ![]() , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна ![]() Найдите
Найдите ![]()
20. Задание 16 № 340078 В треугольнике ABC угол C равен
90°, AC = 4, tg A = 0,75. Найдите BC.
В треугольнике ABC угол C равен
90°, AC = 4, tg A = 0,75. Найдите BC.
21. Задание 16 № 340 В треугольнике
В треугольнике ![]()
![]() = 35,
= 35, ![]() угол
угол ![]() равен 90°. Найдите радиус описанной окружности
этого треугольника.
равен 90°. Найдите радиус описанной окружности
этого треугольника.
22. Задание 16 № 341![]() Найдите площадь прямоугольного треугольника, если его
катет и гипотенуза равны соответственно 12 и 13.
Найдите площадь прямоугольного треугольника, если его
катет и гипотенуза равны соответственно 12 и 13.
23. Задание 16 № 348![]() Катеты прямоугольного треугольника равны 8 и 15. Найдите
гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 8 и 15. Найдите
гипотенузу этого треугольника.
24. Задание 16 № 34841![]() В прямоугольном треугольнике катет и гипотенуза равны 40 и
41 соответственно. Найдите другой катет этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны 40 и
41 соответственно. Найдите другой катет этого треугольника.
25. Задание 16 № 34843![]() В прямоугольном треугольнике катет и гипотенуза равны 40 и
50 соответственно. Найдите другой катет этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны 40 и
50 соответственно. Найдите другой катет этого треугольника.
26. Задание 16 № 3486 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
27. Задание 16 № 34875![]() Один из острых углов прямоугольного треугольника равен 23°.
Найдите его другой острый угол. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 23°.
Найдите его другой острый угол. Ответ дайте в градусах.
28. Задание 16 № 3488 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
29. Задание 16 № 348945 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
30. Задание 16 № 3489 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
31. Задание 16 № 34900 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
32. Задание 16 № 3490 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
33. Задание 16 № 3490 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
34. Задание 16 № 3490 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
35. Задание 16 № 3491 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
36. Задание 16 № 3491 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
37. Задание 16 № 3491 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
38. Задание 16 № 3492 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
39. Задание 16 № 3492 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
40. Задание 16 № 3493 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
41. Задание 16 № 3494 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
42. Задание 16 № 34948![]() Один из острых углов прямоугольного треугольника равен 21°.
Найдите его другой острый угол. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 21°.
Найдите его другой острый угол. Ответ дайте в градусах.
43. Задание 16 № 3494 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
44. Задание 16 № 349522 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
45. Задание 16 № 34952![]() Один из острых углов прямоугольного треугольника равен 43°.
Найдите его другой острый угол. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 43°.
Найдите его другой острый угол. Ответ дайте в градусах.
46. Задание 16 № 3495 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
47. Задание 16 № 3495 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
48. Задание 16 № 349686 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
49. Задание 16 № 349![]() Один из острых углов прямоугольного треугольника равен 63°.
Найдите его другой острый угол. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 63°.
Найдите его другой острый угол. Ответ дайте в градусах.
50. Задание 16 № 34979![]() В прямоугольном треугольнике катет и гипотенуза равны 5 и
13 соответственно. Найдите другой катет этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны 5 и
13 соответственно. Найдите другой катет этого треугольника.
51. Задание 16 № 3498 В треугольнике
В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() , угол
, угол ![]() равен 90°. Найдите радиус описанной окружности этого
треугольника.
равен 90°. Найдите радиус описанной окружности этого
треугольника.
52. Задание 16 № 349![]() Два катета прямоугольного треугольника равны 16 и 30.
Найдите гипотенузу этого треугольника.
Два катета прямоугольного треугольника равны 16 и 30.
Найдите гипотенузу этого треугольника.
53. Задание 16 № 349![]() Один из острых углов прямоугольного треугольника равен 57°.
Найдите его другой острый угол. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 57°.
Найдите его другой острый угол. Ответ дайте в градусах.
54. Задание 16 № 3500 В треугольнике
В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
55. Задание 16 № 353514Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABCк гипотенузе AC. Найдите AB, если AH = 8, AC = 32.
Параллелограмм
1. Задание 16 № 141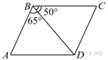 Диагональ BD параллелограмма ABCD образует
с его сторонами углы, равные 65° и 50°. Найдите меньший угол
параллелограмма.
Диагональ BD параллелограмма ABCD образует
с его сторонами углы, равные 65° и 50°. Найдите меньший угол
параллелограмма.
2. Задание 16 № 132Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
3. Задание 16 № 132Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
4. Задание 16 № 31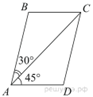 Диагональ AC параллелограмма ABCD
образует с его сторонами углы, равные 30° и 45°. Найдите больший угол
параллелограмма.
Диагональ AC параллелограмма ABCD
образует с его сторонами углы, равные 30° и 45°. Найдите больший угол
параллелограмма.
5. Задание 16 № 311459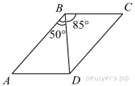 Диагональ BD параллелограмма ABCD
образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол
параллелограмма.
Диагональ BD параллелограмма ABCD
образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол
параллелограмма.
6. Задание 16 № 311911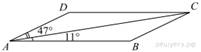 В параллелограмме ABCD проведена
диагональ AC. Угол DAC равен 47°, а угол CAB равен
11°. Найдите больший угол параллелограмма ABCD. Ответ дайте
в градусах.
В параллелограмме ABCD проведена
диагональ AC. Угол DAC равен 47°, а угол CAB равен
11°. Найдите больший угол параллелограмма ABCD. Ответ дайте
в градусах.
7. Задание 16 № 314838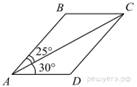 Диагональ AC параллелограмма ABCD образует
с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует
с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
8. Задание 16 № 315038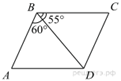 Диагональ BD параллелограмма ABCD образует
с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует
с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма.
9. Задание 16 № 315068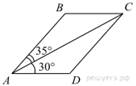 Диагональ AC параллелограмма ABCD образует
с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует
с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
10. Задание 16 № 316345На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.
11. Задание 16 № 324828В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
12. Задание 16 № 339381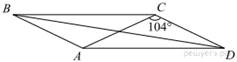 В параллелограмме ABCD диагональ AC в
2 раза больше стороны AB и ∠ACD = 104°. Найдите угол между диагоналями
параллелограмма. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в
2 раза больше стороны AB и ∠ACD = 104°. Найдите угол между диагоналями
параллелограмма. Ответ дайте в градусах.
13. Задание 16 № 340156 Найдите величину острого угла параллелограмма ABCD,
если биссектриса угла A образует со стороной BC угол,
равный 15°. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD,
если биссектриса угла A образует со стороной BC угол,
равный 15°. Ответ дайте в градусах.
14. Задание 16 № 348573 >Найдите острый угол параллелограмма
>Найдите острый угол параллелограмма ![]() , если биссектриса угла
, если биссектриса угла ![]() образует со стороной
образует со стороной ![]() угол, равный 33°. Ответ дайте в градусах.
угол, равный 33°. Ответ дайте в градусах.
15. Задание 16 № 348588 Найдите величину острого угла параллелограмма
Найдите величину острого угла параллелограмма ![]() , если биссектриса угла
, если биссектриса угла ![]() образует со стороной
образует со стороной ![]() угол, равный 31°. Ответ дайте в градусах.
угол, равный 31°. Ответ дайте в градусах.
16. Задание 16 № 348634![]() В параллелограмме
В параллелограмме ![]() диагональ
диагональ ![]() в 2 раза больше стороны
в 2 раза больше стороны ![]() и
и ![]() . Найдите угол между диагоналями параллелограмма. Ответ
дайте в градусах.
. Найдите угол между диагоналями параллелограмма. Ответ
дайте в градусах.
17. Задание 16 № 348637 Найдите величину острого угла параллелограмма
Найдите величину острого угла параллелограмма ![]() , если биссектриса угла
, если биссектриса угла ![]() образует со стороной
образует со стороной ![]() угол, равный 14°. Ответ дайте в градусах.
угол, равный 14°. Ответ дайте в градусах.
18. Задание 16 № 348656 Найдите острый угол параллелограмма
Найдите острый угол параллелограмма ![]() , если биссектриса угла
, если биссектриса угла ![]() образует со стороной
образует со стороной ![]() угол, равный 41°. Ответ дайте в градусах.
угол, равный 41°. Ответ дайте в градусах.
19. Задание 16 № 34868 В параллелограмме
В параллелограмме ![]() диагональ
диагональ ![]() в 2 раза больше стороны
в 2 раза больше стороны ![]() и
и ![]() . Найдите угол между диагоналями параллелограмма. Ответ
дайте в градусах.
. Найдите угол между диагоналями параллелограмма. Ответ
дайте в градусах.
20. Задание 16 № 348768![]() В параллелограмме
В параллелограмме ![]() диагональ
диагональ ![]() в 2 раза больше стороны
в 2 раза больше стороны ![]() и
и ![]() . Найдите угол между диагоналями параллелограмма. Ответ
дайте в градусах.
. Найдите угол между диагоналями параллелограмма. Ответ
дайте в градусах.
21. Задание 16 № 349363 Найдите величину острого угла параллелограмма ABCD,
если биссектриса угла A образует со стороной BC угол,
равный 13°. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD,
если биссектриса угла A образует со стороной BC угол,
равный 13°. Ответ дайте в градусах.
22. Задание 16 № 349397 В параллелограмме ABCD диагональ AC в
2 раза больше стороны AB и ∠ACD = 17°. Найдите меньший угол между диагоналями
параллелограмма. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в
2 раза больше стороны AB и ∠ACD = 17°. Найдите меньший угол между диагоналями
параллелограмма. Ответ дайте в градусах.
23. Задание 16 № 350063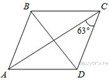 В параллелограмме ABCD диагональ AC в
2 раза больше стороны AB и ∠ACD = 63°. Найдите угол между диагоналями
параллелограмма. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в
2 раза больше стороны AB и ∠ACD = 63°. Найдите угол между диагоналями
параллелограмма. Ответ дайте в градусах.
24. Задание 16 № 352796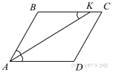 Биссектриса угла A параллелограмма ABCD пересекает
сторону BC в точке K. Найдите периметр
параллелограмма, если BK = 6, CK = 10.
Биссектриса угла A параллелограмма ABCD пересекает
сторону BC в точке K. Найдите периметр
параллелограмма, если BK = 6, CK = 10.
Ромб
1. Задание 16 № 314![]() Сторона ромба равна 34, а острый угол равен 60° . Высота
ромба, опущенная из вершины тупого угла, делит сторону на два отрезка.
Каковы длины этих отрезков?
Сторона ромба равна 34, а острый угол равен 60° . Высота
ромба, опущенная из вершины тупого угла, делит сторону на два отрезка.
Каковы длины этих отрезков?
Перечислите эти длины в ответе без пробелов в порядке возрастания.
2. Задание 16 № 323937Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
3. Задание 16 № 33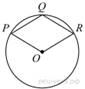 очка O — центр окружности, на которой
лежат точки P, Q и R таким образом, что OPQR —
ромб. Найдите угол ORQ. Ответ дайте в градусах.
очка O — центр окружности, на которой
лежат точки P, Q и R таким образом, что OPQR —
ромб. Найдите угол ORQ. Ответ дайте в градусах.
4. Задание 16 № 33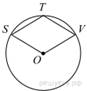 Точка O — центр окружности, на которой
лежат точки S, T и V таким образом, что OSTV —
ромб. Найдите угол STV. Ответ дайте в градусах.
Точка O — центр окружности, на которой
лежат точки S, T и V таким образом, что OSTV —
ромб. Найдите угол STV. Ответ дайте в градусах.
5. Задание 16 № 348371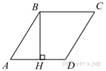 Высота BH ромба ABCD делит
его сторону AD на отрезки AH = 44
и HD = 11. Найдите площадь ромба.
Высота BH ромба ABCD делит
его сторону AD на отрезки AH = 44
и HD = 11. Найдите площадь ромба.
Трапеция
1. Задание 16 № 89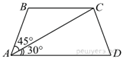 Найдите больший угол равнобедренной трапеции ABCD,
если диагональ AC образует с основанием AD и
боковой стороной AB углы, равные 30° и 45°
соответственно.
Найдите больший угол равнобедренной трапеции ABCD,
если диагональ AC образует с основанием AD и
боковой стороной AB углы, равные 30° и 45°
соответственно.
2. Задание 16 № 193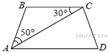 Найдите угол АDС равнобедренной трапеции ABCD,
если диагональ АС образует с основанием ВС и
боковой стороной АВ углы, равные 30° и 50°
соответственно.
Найдите угол АDС равнобедренной трапеции ABCD,
если диагональ АС образует с основанием ВС и
боковой стороной АВ углы, равные 30° и 50°
соответственно.
3. Задание 16 № 132776Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
4. Задание 16 № 132777Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
5. Задание 16 № 132778Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
6. Задание 16 № 311411Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
7. Задание 16 № 311455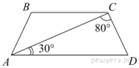 Найдите угол ABC равнобедренной трапеции
ABCD, если диагональ AC образует с основанием
AD и боковой стороной CD углы, равные
30° и 80° соответственно.
Найдите угол ABC равнобедренной трапеции
ABCD, если диагональ AC образует с основанием
AD и боковой стороной CD углы, равные
30° и 80° соответственно.
8. Задание 16 № 311457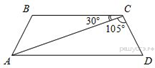 Найдите меньший угол равнобедренной трапеции ABCD,
если диагональ AC образует с основанием BC
и боковой стороной CD углы, равные 30° и 105°
соответственно.
Найдите меньший угол равнобедренной трапеции ABCD,
если диагональ AC образует с основанием BC
и боковой стороной CD углы, равные 30° и 105°
соответственно.
9. Задание 16 № 3119![]() Тангенс острого угла прямоугольной трапеции равен
Тангенс острого угла прямоугольной трапеции равен
![]() Найдите её большее основание, если меньшее основание
равно высоте и равно 15.
Найдите её большее основание, если меньшее основание
равно высоте и равно 15.
10. Задание 16 № 314846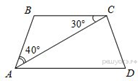 Найдите угол АDС равнобедренной трапеции ABCD,
если диагональ АС образует с основанием ВС и
боковой стороной АВ углы, равные 30° и 40° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD,
если диагональ АС образует с основанием ВС и
боковой стороной АВ углы, равные 30° и 40° соответственно.
11. Задание 16 № 314863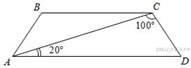 Найдите угол АВС равнобедренной трапеции ABCD,если
диагональ АС образует с основанием AD и
боковой стороной CD углы, равные 20° и 100° соответственно.
Найдите угол АВС равнобедренной трапеции ABCD,если
диагональ АС образует с основанием AD и
боковой стороной CD углы, равные 20° и 100° соответственно.
12. Задание 16 № 315005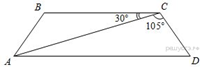 Найдите меньший угол равнобедренной трапеции ABCD,
если диагональ АС образует с основанием ВС и
боковой стороной CD углы, равные 30° и 105° соответственно.
Найдите меньший угол равнобедренной трапеции ABCD,
если диагональ АС образует с основанием ВС и
боковой стороной CD углы, равные 30° и 105° соответственно.
13. Задание 16 № 315099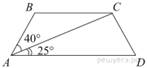 Найдите больший угол равнобедренной трапеции ABCD,
если диагональ АС образует с основанием AD и
боковой стороной АВ углы, равные 25° и 40° соответственно.
Найдите больший угол равнобедренной трапеции ABCD,
если диагональ АС образует с основанием AD и
боковой стороной АВ углы, равные 25° и 40° соответственно.
14. Задание 16 № 323796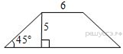 В равнобедренной трапеции известны высота, меньшее
основание и угол при основании. Найдите большее основание.
В равнобедренной трапеции известны высота, меньшее
основание и угол при основании. Найдите большее основание.
15. Задание 16 № 32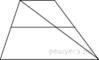 Основания трапеции равны 4 и 10. Найдите больший из
отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Основания трапеции равны 4 и 10. Найдите больший из
отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
16. Задание 16 № 3239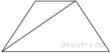 Основания равнобедренной трапеции равны 50 и 104,
боковая сторона 45. Найдите длину диагонали трапеции.
Основания равнобедренной трапеции равны 50 и 104,
боковая сторона 45. Найдите длину диагонали трапеции.
17. Задание 16 № 324838Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Запишите величины углов в твет без пробелов в порядке неубывания.
18. Задание 16 № 324839В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
19. Задание 16 № 339415Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 24, BF = 32.
20. Задание 16 № 339621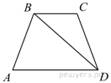 В трапеции ABCD AB = CD,
∠BDA = 49° и ∠BDC = 13°.
Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB = CD,
∠BDA = 49° и ∠BDC = 13°.
Найдите угол ABD. Ответ дайте в градусах.
21. Задание 16 № 34014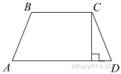 Высота равнобедренной трапеции, проведённая из вершины C,
делит основание AD на отрезки длиной 1 и 5. Найдите
длину основания BC.
Высота равнобедренной трапеции, проведённая из вершины C,
делит основание AD на отрезки длиной 1 и 5. Найдите
длину основания BC.
Многоугольники
1. Задание 16 № 132779Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
2. Задание 16 № 132781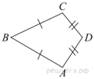 В выпуклом четырехугольнике ABCD
В выпуклом четырехугольнике ABCD ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Найдите угол A. Ответ дайте в градусах.
. Найдите угол A. Ответ дайте в градусах.
3. Задание 16 № 132782Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.
4. Задание 16 № 132783Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
5. Задание 16 № 311759Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.
6. Задание 16 № 339394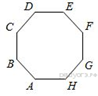 ABCDEFGH — правильный
восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
ABCDEFGH — правильный
восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
7. Задание 16 № 339502 Радиус окружности с центром в точке O равен
85, длина хорды ABравна 80 (см. рисунок). Найдите расстояние
от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен
85, длина хорды ABравна 80 (см. рисунок). Найдите расстояние
от хорды AB до параллельной ей касательной k.
8. Задание 16 № 33950 Сторона AC треугольника ABC проходит
через центр описанной около него окружности. Найдите ∠C, если ∠A = 75°.
Ответ дайте в градусах.
Сторона AC треугольника ABC проходит
через центр описанной около него окружности. Найдите ∠C, если ∠A = 75°.
Ответ дайте в градусах.
9. Задание 16 № 33998 В выпуклом четырехугольнике ABCD AB = BC, AD = CD,
∠B = 77°, ∠D = 141°.
Найдите угол A. Ответ дайте в градусах.
В выпуклом четырехугольнике ABCD AB = BC, AD = CD,
∠B = 77°, ∠D = 141°.
Найдите угол A. Ответ дайте в градусах.
10. Задание 16 № 3401 На стороне BC прямоугольника ABCD,
у которого AB = 12 и AD = 17, отмечена
точка E так, что ∠EAB = 45°. Найдите ED.
На стороне BC прямоугольника ABCD,
у которого AB = 12 и AD = 17, отмечена
точка E так, что ∠EAB = 45°. Найдите ED.
11. Задание 16 № 348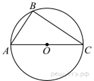 Сторона
Сторона ![]() треугольника
треугольника ![]() проходит через центр описанной около него окружности.
Найдите
проходит через центр описанной около него окружности.
Найдите ![]() , если
, если ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
Центральные и вписанные углы
1. Задание 17 № 90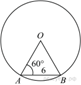 Центральный угол AOB опирается на
хорду AB длиной 6. При этом угол OAB равен 60°.
Найдите радиус окружности.
Центральный угол AOB опирается на
хорду AB длиной 6. При этом угол OAB равен 60°.
Найдите радиус окружности.
2. Задание 17 № 142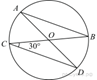 В окружности с центром в точке О проведены
диаметры AD и BC, угол OCD равен
30°. Найдите величину угла OAB.
В окружности с центром в точке О проведены
диаметры AD и BC, угол OCD равен
30°. Найдите величину угла OAB.
3. Задание 17 № 3113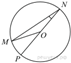 Найдите градусную меру центрального ∠MON, если
известно, NP — диаметр, а градусная мера ∠MNP равна 18°.
Найдите градусную меру центрального ∠MON, если
известно, NP — диаметр, а градусная мера ∠MNP равна 18°.
4. Задание 17 № 311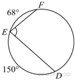 Найдите ∠DEF, если градусные меры дуг DE и EF равны
150° и 68° соответственно.
Найдите ∠DEF, если градусные меры дуг DE и EF равны
150° и 68° соответственно.
5. Задание 17 № 31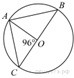 Найдите градусную меру ∠ACB, если известно,
что BC является диаметром окружности, а градусная мера
цетрального ∠AOC равна 96°.
Найдите градусную меру ∠ACB, если известно,
что BC является диаметром окружности, а градусная мера
цетрального ∠AOC равна 96°.
6. Задание 17 № 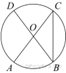 В окружности с центром O AC и BD —
диаметры. Угол ACB равен 26°. Найдите угол AOD.
Ответ дайте в градусах.
В окружности с центром O AC и BD —
диаметры. Угол ACB равен 26°. Найдите угол AOD.
Ответ дайте в градусах.
7. Задание 17 № 311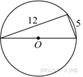 Прямоугольный треугольник с катетами 5 см и 12 см вписан
в окружность. Чему равен радиус этой окружности?
Прямоугольный треугольник с катетами 5 см и 12 см вписан
в окружность. Чему равен радиус этой окружности?
8. Задание 17 № 31148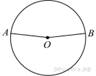 Точки A и B делят окружность
на две дуги, длины которых относятся как 9:11. Найдите величину центрального
угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
Точки A и B делят окружность
на две дуги, длины которых относятся как 9:11. Найдите величину центрального
угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
9. Задание 17 № 311510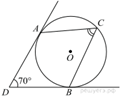 В угол величиной 70° вписана окружность, которая касается
его сторон в точках A и B. На одной из дуг этой
окружности выбрали точку C так, как показано на
рисунке. Найдите величину угла ACB.
В угол величиной 70° вписана окружность, которая касается
его сторон в точках A и B. На одной из дуг этой
окружности выбрали точку C так, как показано на
рисунке. Найдите величину угла ACB.
10. Задание 17 № 3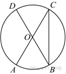 Величина центрального угла AOD равна
110°. Найдите величину вписанного угла ACB. Ответ дайте в
градусах.
Величина центрального угла AOD равна
110°. Найдите величину вписанного угла ACB. Ответ дайте в
градусах.
11. Задание 17 № 31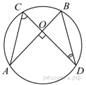 Точки A, B, C и D лежат
на одной окружности так, что хорды AB и СD взаимно
перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.
Точки A, B, C и D лежат
на одной окружности так, что хорды AB и СD взаимно
перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.
12. Задание 17 № Треугольник ABC вписан в окружность с
центром в точке O. Найдите градусную меру угла C треугольника ABC,
если угол AOB равен 48°.
Треугольник ABC вписан в окружность с
центром в точке O. Найдите градусную меру угла C треугольника ABC,
если угол AOB равен 48°.
13. Задание 17 № 31 Точка О — центр окружности, ∠AOB = 84° (см. рисунок).
Найдите величину угла ACB (в градусах).
Точка О — центр окружности, ∠AOB = 84° (см. рисунок).
Найдите величину угла ACB (в градусах).
14. Задание 17 № 33 На окружности с центром O отмечены
точки A и B так, что
На окружности с центром O отмечены
точки A и B так, что ![]() Длина меньшей дуги AB равна 63. Найдите
длину большей дуги.
Длина меньшей дуги AB равна 63. Найдите
длину большей дуги.
15. Задание 17 № 3394 На окружности по разные стороны от диаметра AB взяты
точки M и N. Известно, что ∠NBA = 38°.
Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты
точки M и N. Известно, что ∠NBA = 38°.
Найдите угол NMB. Ответ дайте в градусах.
16. Задание 17 № 33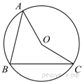 Точка O – центр окружности, на которой
лежат точки A, B и C. Известно, что ∠ABC = 15° и ∠OAB = 8°.
Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой
лежат точки A, B и C. Известно, что ∠ABC = 15° и ∠OAB = 8°.
Найдите угол BCO. Ответ дайте в градусах.
17. Задание 17 №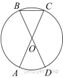 AC и BD —
диаметры окружности с центром O. Угол ACB равен
79°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD —
диаметры окружности с центром O. Угол ACB равен
79°. Найдите угол AOD. Ответ дайте в градусах.
18. Задание 17 № 34022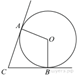 В угол C величиной 83° вписана
окружность, которая касается сторон угла в точках A и B.
Найдите угол AOB. Ответ дайте в градусах.
В угол C величиной 83° вписана
окружность, которая касается сторон угла в точках A и B.
Найдите угол AOB. Ответ дайте в градусах.
19. Задание 17 № 34135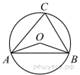 Треугольник ABC вписан в окружность с
центром в точке O. Найдите градусную меру угла C треугольника ABC,
если угол AOB равен 115°.
Треугольник ABC вписан в окружность с
центром в точке O. Найдите градусную меру угла C треугольника ABC,
если угол AOB равен 115°.
20. Задание 17 № 3416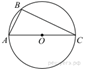 Сторона AC треугольника ABC содержит
центр описанной около него окружности. Найдите
Сторона AC треугольника ABC содержит
центр описанной около него окружности. Найдите ![]() , если
, если ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
21. Задание 17 № 3483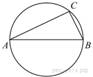 Центр окружности, описанной около треугольника ABC,
лежит на стороне AB. Найдите угол ABC, если угол BAC равен
30°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC,
лежит на стороне AB. Найдите угол ABC, если угол BAC равен
30°. Ответ дайте в градусах.
22. Задание 17 № 348493На окружности с центром в точке ![]() отмечены точки
отмечены точки ![]() и
и ![]() так, что
так, что ![]() . Длина меньшей дуги
. Длина меньшей дуги ![]() равна 50. Найдите длину большей дуги
равна 50. Найдите длину большей дуги ![]() .
.
23. Задание 17 № 3485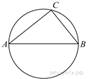 Центр окружности, описанной около треугольника
Центр окружности, описанной около треугольника ![]() , лежит на стороне
, лежит на стороне ![]() . Найдите угол
. Найдите угол ![]() , если угол
, если угол ![]() равен 44°. Ответ дайте в градусах.
равен 44°. Ответ дайте в градусах.
24. Задание 17 № 34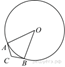 В угол
В угол ![]() величиной 157° вписана окружность, которая касается
сторон угла в точках
величиной 157° вписана окружность, которая касается
сторон угла в точках ![]() и
и ![]() , точка
, точка ![]() — центр окружности. Найдите угол
— центр окружности. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
25. Задание 17 № 34 На окружности с центром в точке
На окружности с центром в точке ![]() отмечены точки
отмечены точки ![]() и
и ![]() так, что
так, что ![]() . Длина меньшей дуги
. Длина меньшей дуги ![]() равна 5. Найдите длину большей дуги
равна 5. Найдите длину большей дуги ![]() .
.
26. Задание 17 № 348 На окружности с центром в точке
На окружности с центром в точке ![]() отмечены точки
отмечены точки ![]() и
и ![]() так, что
так, что ![]() . Длина меньшей дуги
. Длина меньшей дуги ![]() равна 61. Найдите длину большей дуги
равна 61. Найдите длину большей дуги ![]() .
.
27. Задание 17 № 3489 Центр окружности, описанной около треугольника
Центр окружности, описанной около треугольника ![]() , лежит на стороне
, лежит на стороне ![]() . Радиус окружности равен 6,5. Найдите
. Радиус окружности равен 6,5. Найдите ![]() , если
, если ![]()
28. Задание 17 № 3489 Центр окружности, описанной около треугольника
Центр окружности, описанной около треугольника ![]() , лежит на стороне
, лежит на стороне ![]() . Радиус окружности равен 8,5. Найдите
. Радиус окружности равен 8,5. Найдите ![]() , если
, если ![]() .
.
29. Задание 17 № 34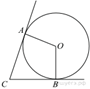 В угол C величиной 72° вписана окружность, которая
касается сторон угла в точках A и B,
точка O - центр окружности. Найдите угол AOB.
Ответ дайте в градусах.
В угол C величиной 72° вписана окружность, которая
касается сторон угла в точках A и B,
точка O - центр окружности. Найдите угол AOB.
Ответ дайте в градусах.
30. Задание 17 № 34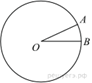 На окружности с центром O отмечены
точки A и B так, что
На окружности с центром O отмечены
точки A и B так, что ![]() Длина меньшей дуги AB равна 98. Найдите
длину большей дуги.
Длина меньшей дуги AB равна 98. Найдите
длину большей дуги.
31. Задание 17 № 349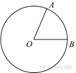 На окружности с центром O отмечены
точки A и B так, что
На окружности с центром O отмечены
точки A и B так, что ![]() Длина меньшей дуги AB равна 58. Найдите
длину большей дуги.
Длина меньшей дуги AB равна 58. Найдите
длину большей дуги.
32. Задание 17 № 34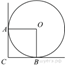 В угол C величиной 90° вписана окружность, которая
касается сторон угла в точках A и B,
точка O - центр окружности. Найдите угол AOB.
Ответ дайте в градусах.
В угол C величиной 90° вписана окружность, которая
касается сторон угла в точках A и B,
точка O - центр окружности. Найдите угол AOB.
Ответ дайте в градусах.
33. Задание 17 № 3 AC и BD —
диаметры окружности с центром O. Угол ACB равен
36°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD —
диаметры окружности с центром O. Угол ACB равен
36°. Найдите угол AOD. Ответ дайте в градусах.
34. Задание 17 № 3 AC и BD —
диаметры окружности с центром O. Угол ACB равен
23°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD —
диаметры окружности с центром O. Угол ACB равен
23°. Найдите угол AOD. Ответ дайте в градусах.
35. Задание 17 № 349453 В угол C величиной 62° вписана окружность, которая
касается сторон угла в точках A и B,
точка O — центр окружности. Найдите угол AOB.
Ответ дайте в градусах.
В угол C величиной 62° вписана окружность, которая
касается сторон угла в точках A и B,
точка O — центр окружности. Найдите угол AOB.
Ответ дайте в градусах.
36. Задание 17 № 3494 Центр окружности, описанной около треугольника ABC,
лежит на стороне AB. Найдите угол ABC, если угол BAC равен
33°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC,
лежит на стороне AB. Найдите угол ABC, если угол BAC равен
33°. Ответ дайте в градусах.
37. Задание 17 № 349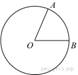 На окружности с центром O отмечены
точки A и B так, что
На окружности с центром O отмечены
точки A и B так, что ![]() Длина меньшей дуги AB равна 57. Найдите
длину большей дуги.
Длина меньшей дуги AB равна 57. Найдите
длину большей дуги.
38. Задание 17 № 3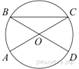 AC и BD —
диаметры окружности с центром O. Угол ACB равен
54°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD —
диаметры окружности с центром O. Угол ACB равен
54°. Найдите угол AOD. Ответ дайте в градусах.
39. Задание 17 № 349689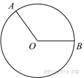 На окружности с центром O отмечены
точки A и B так, что
На окружности с центром O отмечены
точки A и B так, что ![]() Длина меньшей дуги AB равна 67. Найдите
длину большей дуги.
Длина меньшей дуги AB равна 67. Найдите
длину большей дуги.
40. Задание 17 № 3497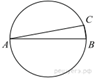 Центр окружности, описанной около треугольника ABC,
лежит на стороне AB. Найдите угол ABC, если угол BAC равен
9°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC,
лежит на стороне AB. Найдите угол ABC, если угол BAC равен
9°. Ответ дайте в градусах.
41. Задание 17 № 3 AC и BD —
диаметры окружности с центром O. Угол ACB равен
19°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD —
диаметры окружности с центром O. Угол ACB равен
19°. Найдите угол AOD. Ответ дайте в градусах.
42. Задание 17 № 34986 AC и BD —
диаметры окружности с центром O. Угол ACB равен
78°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD —
диаметры окружности с центром O. Угол ACB равен
78°. Найдите угол AOD. Ответ дайте в градусах.
43. Задание 17 № 349952
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 24°. Ответ дайте в градусах.
44. Задание 17 № 349998 В угол C величиной 71° вписана окружность, которая
касается сторон угла в точках A и B,
точка O - центр окружности. Найдите угол AOB.
Ответ дайте в градусах.
В угол C величиной 71° вписана окружность, которая
касается сторон угла в точках A и B,
точка O - центр окружности. Найдите угол AOB.
Ответ дайте в градусах.
Касательная, хорда, секущая, радиус
1. Задание 17 № 3114 Радиус OB окружности с центром в
точке O пересекает хорду AC в точке D и
перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см,
а радиус окружности равен 5 см.
Радиус OB окружности с центром в
точке O пересекает хорду AC в точке D и
перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см,
а радиус окружности равен 5 см.
2. Задание 17 № 3114 Найдите величину (в градусах) вписанного угла α,
опирающегося на хорду AB, равную радиусу окружности.
Найдите величину (в градусах) вписанного угла α,
опирающегося на хорду AB, равную радиусу окружности.
3. Задание 17 № 3116 К окружности с центром в точке О проведены
касательная AB и секущая AO. Найдите радиус
окружности, если AB = 12 см, AO = 13 см.
К окружности с центром в точке О проведены
касательная AB и секущая AO. Найдите радиус
окружности, если AB = 12 см, AO = 13 см.
4. Задание 17 № 3119 В треугольнике ABC угол C равен
90°, AC = 30 , BC =
В треугольнике ABC угол C равен
90°, AC = 30 , BC = ![]() Найдите радиус окружности, описанной около
этого треугольника.
Найдите радиус окружности, описанной около
этого треугольника.
5. Задание 17 № 3243 Длина хорды окружности равна 72, а расстояние от центра
окружности до этой хорды равно 27. Найдите диаметр окружности.
Длина хорды окружности равна 72, а расстояние от центра
окружности до этой хорды равно 27. Найдите диаметр окружности.
6. Задание 17 № 3248Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
7. Задание 17 № 3394 Прямая касается окружности в точке K.
Точка O — центр окружности. Хорда KM образует
с касательной угол, равный 83°. Найдите величину угла OMK.
Ответ дайте в градусах.
Прямая касается окружности в точке K.
Точка O — центр окружности. Хорда KM образует
с касательной угол, равный 83°. Найдите величину угла OMK.
Ответ дайте в градусах.
8. Задание 17 № 3396Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
9. Задание 17 № 3398Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.
10. Задание 17 № 339На окружности с центром O отмечены точки A и B так, что ∠AOB = 66°. Длина меньшей дуги ABравна 99. Найдите длину большей дуги.
11. Задание 17 № 339 Отрезок AB = 40 касается окружности
радиуса 75 с центром O в точке B. Окружность
пересекает отрезок AO в точке D. Найдите AD.
Отрезок AB = 40 касается окружности
радиуса 75 с центром O в точке B. Окружность
пересекает отрезок AO в точке D. Найдите AD.
12. Задание 17 № 340 На отрезке AB выбрана точка C так,
что AC = 75 и BC = 10. Построена
окружность с центром A, проходящая через C. Найдите
длину отрезка касательной, проведённой из точки B к этой
окружности.
На отрезке AB выбрана точка C так,
что AC = 75 и BC = 10. Построена
окружность с центром A, проходящая через C. Найдите
длину отрезка касательной, проведённой из точки B к этой
окружности.
13. Задание 17 № 340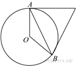 Касательные в точках A и B к
окружности с центром O пересекаются под углом 72°. Найдите
угол ABO. Ответ дайте в градусах.
Касательные в точках A и B к
окружности с центром O пересекаются под углом 72°. Найдите
угол ABO. Ответ дайте в градусах.
14. Задание 17 № 341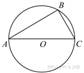 Сторона AC треугольника ABC проходит
через центр описанной около него окружности. Найдите ∠C , если ∠A = 44°. Ответ
дайте в градусах.
Сторона AC треугольника ABC проходит
через центр описанной около него окружности. Найдите ∠C , если ∠A = 44°. Ответ
дайте в градусах.
15. Задание 17 № 341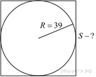 Окружность вписана в квадрат. Найдите площадь
квадрата.
Окружность вписана в квадрат. Найдите площадь
квадрата.
16. Задание 17 № 102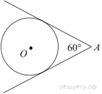 Из точки А проведены две касательные
к окружности с центром в точке О. Найдите радиус окружности,
если угол между касательными равен 60°, а расстояние от точки А до
точки О равно 8.
Из точки А проведены две касательные
к окружности с центром в точке О. Найдите радиус окружности,
если угол между касательными равен 60°, а расстояние от точки А до
точки О равно 8.
17. Задание 17 № 3394Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7,5, а AB = 2.
18. Задание 17 № 3484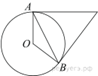 Касательные в точках
Касательные в точках ![]() и
и ![]() к окружности с центром
к окружности с центром ![]() пересекаются под углом 76°. Найдите угол
пересекаются под углом 76°. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
19. Задание 17 № 3485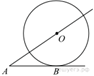 К окружности с центром в точке
К окружности с центром в точке ![]() проведены касательная
проведены касательная ![]() и секущая
и секущая ![]() . Найдите радиус окружности, если
. Найдите радиус окружности, если ![]() ,
, ![]() .
.
20. Задание 17 № 3485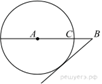 На отрезке
На отрезке ![]() выбрана точка
выбрана точка ![]() так, что
так, что ![]() и
и ![]() . Построена окружность с центром
. Построена окружность с центром ![]() , проходящая через
, проходящая через ![]() . Найдите длину отрезка касательной, проведённой из
точки
. Найдите длину отрезка касательной, проведённой из
точки ![]() к этой окружности.
к этой окружности.
21. Задание 17 № 3486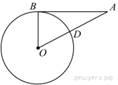 Отрезок
Отрезок ![]() касается окружности радиуса 24 с центром
касается окружности радиуса 24 с центром ![]() в точке
в точке ![]() . Окружность пересекает отрезок
. Окружность пересекает отрезок ![]() в точке
в точке ![]() . Найдите
. Найдите ![]() .
.
22. Задание 17 № 3486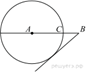 На отрезке
На отрезке ![]() выбрана точка
выбрана точка ![]() так, что
так, что ![]() и
и ![]() . Построена окружность с центром
. Построена окружность с центром ![]() , проходящая через
, проходящая через ![]() . Найдите длину отрезка касательной, проведённой из
точки
. Найдите длину отрезка касательной, проведённой из
точки ![]() к этой окружности.
к этой окружности.
23. Задание 17 № 34873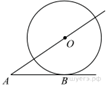 К окружности с центром в точке
К окружности с центром в точке ![]() проведены касательная
проведены касательная ![]() и секущая
и секущая ![]() . Найдите радиус окружности, если
. Найдите радиус окружности, если ![]() ,
, ![]() .
.
24. Задание 17 № 348810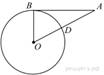 Отрезок
Отрезок ![]() касается окружности радиуса 54 с центром
касается окружности радиуса 54 с центром ![]() в точке
в точке ![]() . Окружность пересекает отрезок
. Окружность пересекает отрезок ![]() в точке
в точке ![]() . Найдите
. Найдите ![]() .
.
25. Задание 17 № 34888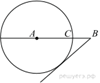 На отрезке
На отрезке ![]() выбрана точка
выбрана точка ![]() так, что
так, что ![]() и
и ![]() . Построена окружность с центром
. Построена окружность с центром ![]() , проходящая через
, проходящая через ![]() . Найдите длину отрезка касательной, проведённой из
точки
. Найдите длину отрезка касательной, проведённой из
точки ![]() к этой окружности.
к этой окружности.
26. Задание 17 № 348951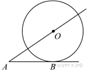 К окружности с центром в точке
К окружности с центром в точке ![]() проведены касательная
проведены касательная ![]() и секущая
и секущая ![]() . Найдите радиус окружности, если
. Найдите радиус окружности, если ![]() ,
, ![]()
27. Задание 17 № 349282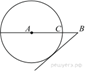 На отрезке
На отрезке ![]() выбрана точка
выбрана точка ![]() так, что
так, что ![]() и
и ![]() . Построена окружность с центром
. Построена окружность с центром ![]() , проходящая через
, проходящая через ![]() . Найдите длину отрезка касательной, проведённой из
точки
. Найдите длину отрезка касательной, проведённой из
точки ![]() к этой окружности.
к этой окружности.
28. Задание 17 № 349760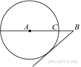 На отрезке
На отрезке ![]() выбрана точка
выбрана точка ![]() так, что
так, что ![]() и
и ![]() . Построена окружность с центром
. Построена окружность с центром ![]() , проходящая через
, проходящая через ![]() . Найдите длину отрезка касательной, проведённой из
точки
. Найдите длину отрезка касательной, проведённой из
точки ![]() к этой окружности.
к этой окружности.
29. Задание 17 № 349963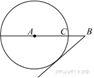 На отрезке
На отрезке ![]() выбрана точка
выбрана точка ![]() так, что
так, что ![]() и
и ![]() . Построена окружность с центром
. Построена окружность с центром ![]() , проходящая через
, проходящая через ![]() . Найдите длину отрезка касательной, проведённой из
точки
. Найдите длину отрезка касательной, проведённой из
точки ![]() к этой окружности.
к этой окружности.
30. Задание 17 № 34998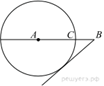 На отрезке
На отрезке ![]() выбрана точка
выбрана точка ![]() так, что
так, что ![]() и
и ![]() . Построена окружность с центром
. Построена окружность с центром ![]() , проходящая через
, проходящая через ![]() . Найдите длину отрезка касательной, проведённой из
точки
. Найдите длину отрезка касательной, проведённой из
точки ![]() к этой окружности.
к этой окружности.
31. Задание 17 № 355413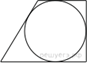 Радиус окружности, вписанной в трапецию, равен 16. Найдите
высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 16. Найдите
высоту этой трапеции.
Окружность, описанная вокруг многоугольника
1. Задание 17 № 31150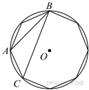 В окружность вписан равносторонний восьмиугольник. Найдите
величину угла ABC.
В окружность вписан равносторонний восьмиугольник. Найдите
величину угла ABC.
2. Задание 17 № 31150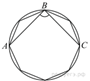
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
3. Задание 17 № 31634Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
4. Задание 17 № 31637Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
5. Задание 17 № 33948
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.
6. Задание 17 № 339828
Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
7. Задание 17 № 341707 Найдите площадь квадрата, описанного вокруг окружности
радиуса 7.
Найдите площадь квадрата, описанного вокруг окружности
радиуса 7.
Квадрат
1. Задание 18 № 16986Сторона квадрата равна 10. Найдите его площадь.
2. Задание 18 № 16986Периметр квадрата равен 40. Найдите площадь квадрата.
3. Задание 18 № 32286
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
4. Задание 18 № 32397 Периметр квадрата равен 160. Найдите площадь квадрата.
Периметр квадрата равен 160. Найдите площадь квадрата.
5. Задание 18 № 323997 Найдите площадь квадрата, если его диагональ равна
1.
Найдите площадь квадрата, если его диагональ равна
1.
6. Задание 18 № 324364 Найдите площадь квадрата, описанного вокруг окружности
радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности
радиуса 83.
Прямоугольник
1. Задание 18 № 169864В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
2. Задание 18 № 169867В прямоугольнике диагональ равна 10, а угол между ней и
одной из сторон равен 30°. Найдите площадь прямоугольника, делённую
на ![]() .
.
3. Задание 18 № 169898В прямоугольнике диагональ равна 10, угол между ней и
одной из сторон равен 30°, длина этой стороны ![]() . Найдите площадь прямоугольника, деленную на
. Найдите площадь прямоугольника, деленную на ![]()
4. Задание 18 № 311761Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
5. Задание 18 № 311849Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
6. Задание 18 № 316321Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
7. Задание 18 № 324077 В прямоугольнике одна сторона равна 96, а диагональ
равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ
равна 100. Найдите площадь прямоугольника.
Параллелограмм
1. Задание 18 № 65 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
2. Задание 18 № 169868Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
3. Задание 18 № 169869Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
4. Задание 18 № 169872Периметр ромба равен 24, а синус одного из углов
равен ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
5. Задание 18 № 169875Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
6. Задание 18 № 169876Одна из сторон параллелограмма равна 12, другая равна 5,
а один из углов — 45°. Найдите площадь параллелограмма, делённую
на ![]() .
.
7. Задание 18 № 169878Одна из сторон параллелограмма равна 12, другая равна 5,
а синус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
8. Задание 18 № 169879Одна из сторон параллелограмма равна 12, другая равна 5,
а косинус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
9. Задание 18 № 169880Одна из сторон параллелограмма равна 12, другая равна 5,
а тангенс одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
10. Задание 18 № 169900В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали,
равен 30°. Найдите площадь ромба.
, а угол, лежащий напротив этой диагонали,
равен 30°. Найдите площадь ромба.
11. Задание 18 № 314870 Площадь параллелограмма ABCD равна
56. Точка E — середина стороны CD. Найдите
площадь трапеции AECB.
Площадь параллелограмма ABCD равна
56. Точка E — середина стороны CD. Найдите
площадь трапеции AECB.
12. Задание 18 № 3239![]() Найдите площадь ромба, если его диагонали равны 14 и
6.
Найдите площадь ромба, если его диагонали равны 14 и
6.
13. Задание 18 № 3240 Сторона ромба равна 9, а расстояние от центра ромба
до неё равно 1. Найдите площадь ромба.
Сторона ромба равна 9, а расстояние от центра ромба
до неё равно 1. Найдите площадь ромба.
14. Задание 18 № 3240![]() Сторона ромба равна 50, а диагональ равна 80. Найдите
площадь ромба.
Сторона ромба равна 50, а диагональ равна 80. Найдите
площадь ромба.
15. Задание 18 № 3241![]() Периметр ромба равен 116, а один из углов равен 30°. Найдите
площадь ромба.
Периметр ромба равен 116, а один из углов равен 30°. Найдите
площадь ромба.
16. Задание 18 № 3398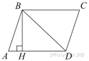 Высота BH параллелограмма ABCD делит
его сторону AD на отрезки AH = 1
и HD = 28. Диагональ параллелограмма BD равна
53. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит
его сторону AD на отрезки AH = 1
и HD = 28. Диагональ параллелограмма BD равна
53. Найдите площадь параллелограмма.
17. Задание 18 № 3403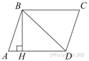 Высота BH ромба ABCD делит
его сторону AD на отрезки AH = 5
и HD = 8. Найдите площадь ромба.
Высота BH ромба ABCD делит
его сторону AD на отрезки AH = 5
и HD = 8. Найдите площадь ромба.
18. Задание 18 № 341523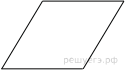 Площадь ромба равна 54, а периметр равен 36. Найдите высоту
ромба.
Площадь ромба равна 54, а периметр равен 36. Найдите высоту
ромба.
19. Задание 18 № 348821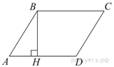 Высота
Высота ![]() ромба
ромба ![]() делит его сторону
делит его сторону ![]() на отрезки
на отрезки ![]() и
и ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
Треугольники общего вида
1. Задание 18 № 169853В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
2. Задание 18 № 169854В треугольнике одна из сторон равна 10, другая
равна ![]() , а угол между ними равен 60°. Найдите площадь
треугольника.
, а угол между ними равен 60°. Найдите площадь
треугольника.
3. Задание 18 № 323436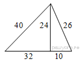 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
4. Задание 18 № 341524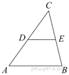 В треугольнике ABC отрезок DE —
средняя линия. Площадь треугольника CDE равна 97. Найдите
площадь треугольника ABC.
В треугольнике ABC отрезок DE —
средняя линия. Площадь треугольника CDE равна 97. Найдите
площадь треугольника ABC.
5. Задание 18 № 349889Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.
Прямоугольный треугольник
1. Задание 18 № 16984В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
2. Задание 18 № 16988В прямоугольном треугольнике один из катетов равен 10,
острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите
площадь треугольника, делённую на ![]() .
.
3. Задание 18 № 32315Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
4. Задание 18 № 32328В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
5. Задание 18 № 32335 В прямоугольном треугольнике гипотенуза равна 70,
а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70,
а один из острых углов равен 45°. Найдите площадь треугольника.
6. Задание 18 № 34855![]()
Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.
Равнобедренный треугольник
1. Задание 18 № 169847Сторона равностороннего треугольника равна 10. Найдите
его площадь, делённую на ![]() .
.
2. Задание 18 № 169848Периметр равностороннего треугольника равен 30. Найдите
его площадь, делённую на ![]() .
.
3. Задание 18 № 169849Высота равностороннего треугольника равна 10. Найдите
его площадь, делённую на ![]()
4. Задание 18 № 169850В равнобедренном треугольнике боковая сторона равна
10, а угол, лежащий напротив основания, равен 120°. Найдите площадь
треугольника, делённую на ![]()
5. Задание 18 № 169851Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
6. Задание 18 № 16989В равнобедренном треугольнике боковая сторона равна
10, основание — ![]() , а угол, лежащий напротив основания, равен 30°. Найдите
площадь треугольника.
, а угол, лежащий напротив основания, равен 30°. Найдите
площадь треугольника.
7. Задание 18 № 32317![]() Боковая сторона равнобедренного треугольника
равна 34, а основание равно 60. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника
равна 34, а основание равно 60. Найдите площадь этого треугольника.
8. Задание 18 № 323396 Периметр равнобедренного треугольника равен 216,
а боковая сторона — 78. Найдите площадь треугольника.
Периметр равнобедренного треугольника равен 216,
а боковая сторона — 78. Найдите площадь треугольника.
Трапеция
1. Задание 18 № 39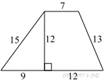 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
2. Задание 18 № 117 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
3. Задание 18 № 143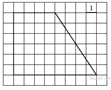 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
4. Задание 18 № 169881Основания трапеции равны 18 и 12, одна из боковых
сторон равна ![]() , а угол между ней и одним из оснований равен 135°. Найдите
площадь трапеции.
, а угол между ней и одним из оснований равен 135°. Найдите
площадь трапеции.
5. Задание 18 № 169883Основания трапеции равны 18 и 12, одна из боковых
сторон равна 6, а синус угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
6. Задание 18 № 169884Основания трапеции равны 18 и 12, одна из боковых
сторон равна 6, а косинус угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
7. Задание 18 № 169885Основания трапеции равны 18 и 12, одна из боковых
сторон равна 6, а тангенс угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
8. Задание 18 № 311480 Средняя линия трапеции равна 11, а меньшее основание
равно 5. Найдите большее основание трапеции.
Средняя линия трапеции равна 11, а меньшее основание
равно 5. Найдите большее основание трапеции.
9. Задание 18 № 311682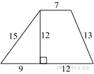 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
10. Задание 18 № 314876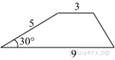 Боковая сторона трапеции равна 5, а один из прилегающих
к ней углов равен 30°. Найдите площадь трапеции, если её основания
равны 3 и 9.
Боковая сторона трапеции равна 5, а один из прилегающих
к ней углов равен 30°. Найдите площадь трапеции, если её основания
равны 3 и 9.
11. Задание 18 № 3148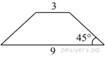 В равнобедренной трапеции основания равны 3 и 9, а
один из углов между боковой стороной и основанием равен 45°. Найдите
площадь трапеции.
В равнобедренной трапеции основания равны 3 и 9, а
один из углов между боковой стороной и основанием равен 45°. Найдите
площадь трапеции.
12. Задание 18 №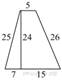 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
13. Задание 18 № 31637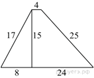 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
14. Задание 18 № 32![]() Основания равнобедренной трапеции равны 5 и 17, а
ее боковые стороны равны 10. Найдите площадь трапеции.
Основания равнобедренной трапеции равны 5 и 17, а
ее боковые стороны равны 10. Найдите площадь трапеции.
15. Задание 18 № 3241![]() Основания трапеции равны 7 и 49, одна из боковых сторон
равна 18 , а косинус угла между ней и одним из оснований равен
Основания трапеции равны 7 и 49, одна из боковых сторон
равна 18 , а косинус угла между ней и одним из оснований равен ![]() Найдите площадь трапеции.
Найдите площадь трапеции.
16. Задание 18 № 3398![]() Основания трапеции равны 1 и 13, одна из боковых сторон
равна
Основания трапеции равны 1 и 13, одна из боковых сторон
равна ![]() , а угол между ней и одним из оснований равен 135°. Найдите
площадь трапеции.
, а угол между ней и одним из оснований равен 135°. Найдите
площадь трапеции.
17. Задание 18 № 3401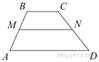 В трапеции ABCD AD = 5, BC = 2,
а её площадь равна 28. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
В трапеции ABCD AD = 5, BC = 2,
а её площадь равна 28. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
18. Задание 18 № 3404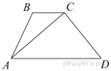 В трапеции ABCD AD = 3, BC = 1,
а её площадь равна 12. Найдите площадь треугольника ABC.
В трапеции ABCD AD = 3, BC = 1,
а её площадь равна 12. Найдите площадь треугольника ABC.
19. Задание 18 № 341356![]() Тангенс острого угла прямоугольной трапеции равен
Тангенс острого угла прямоугольной трапеции равен ![]() Найдите её большее основание, если меньшее основание
равно высоте и равно 58.
Найдите её большее основание, если меньшее основание
равно высоте и равно 58.
20. Задание 18 № 341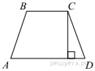 Высота равнобедренной трапеции, проведённая из вершины C,
делит основание AD на отрезки длиной 2 и 9. Найдите
длину основания BC.
Высота равнобедренной трапеции, проведённая из вершины C,
делит основание AD на отрезки длиной 2 и 9. Найдите
длину основания BC.
21. Задание 18 № 3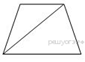 Основания равнобедренной трапеции равны 4 и 14, боковая
сторона равна 13. Найдите длину диагонали трапеции.
Основания равнобедренной трапеции равны 4 и 14, боковая
сторона равна 13. Найдите длину диагонали трапеции.
22. Задание 18 № 348![]() Основания трапеции равны 9 и 54, одна из боковых сторон
равна 27, а косинус угла между ней и одним из оснований равен
Основания трапеции равны 9 и 54, одна из боковых сторон
равна 27, а косинус угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
23. Задание 18 № 3491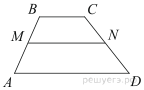 В трапеции ABCD известно, что AD = 6, BC = 2,
а её площадь равна 32. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
В трапеции ABCD известно, что AD = 6, BC = 2,
а её площадь равна 32. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
24. Задание 18 № 3491 В трапеции ABCD известно, что AD = 5, BC = 1,
а её площадь равна 51. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
В трапеции ABCD известно, что AD = 5, BC = 1,
а её площадь равна 51. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
25. Задание 18 № 3492 В трапеции ABCD известно, что AD = 8, BC = 5,
а её площадь равна 52. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
В трапеции ABCD известно, что AD = 8, BC = 5,
а её площадь равна 52. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
26. Задание 18 № 3492 В трапеции ABCD известно, что AD = 2, BC = 1,
а её площадь равна 48. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
В трапеции ABCD известно, что AD = 2, BC = 1,
а её площадь равна 48. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
27. Задание 18 № 3492 В трапеции ABCD известно, что AD = 7, BC = 5,
а её площадь равна 72. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
В трапеции ABCD известно, что AD = 7, BC = 5,
а её площадь равна 72. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
28. Задание 18 № 3495Основания трапеции равны 6 и 24, одна из боковых сторон
равна 11, а синус угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
29. Задание 18 № 3496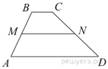 В трапеции ABCD известно, что AD = 5, BC = 1,
а её площадь равна 12. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
В трапеции ABCD известно, что AD = 5, BC = 1,
а её площадь равна 12. Найдите площадь трапеции BCNM,
где MN – средняя линия трапеции ABCD.
30. Задание 18 № 3496Основания трапеции равны 7 и 63, одна из боковых сторон
равна 18, а косинус угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
31. Задание 18 № 34971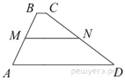
В трапеции ABCD известно, что AD = 9, BC = 1, а её площадь равна 70. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
32. Задание 18 № 351297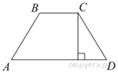
Высота
равнобедренной трапеции, проведённая из вершины ![]() ,
отсекает от основания
,
отсекает от основания ![]() отрезок
длиной 2. Длина основания
отрезок
длиной 2. Длина основания ![]() равна
7. Найдите длину основания
равна
7. Найдите длину основания ![]() .
.
Площадь круга и его частей
1. Задание 18 № 169886Радиус круга равен 1. Найдите его площадь, деленную на π.
2. Задание 18 № 169887Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
3. Задание 18 № 169888Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
4. Задание 18 № 169912Радиус круга равен 3, а длина ограничивающей его окружности равна 6π. Найдите площадь круга. В ответ запишите площадь, деленную на π.
5. Задание 18 № 169913Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите площадь, деленную на π.
Углы
1. Задание 19 № 40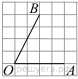
Найдите тангенс угла AOB, изображенного на рисунке.
2. Задание 19 № 31148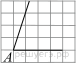
На квадратной
сетке изображён угол ![]() .
Найдите
.
Найдите ![]() .
.
3. Задание 19 № 31634
Найдите тангенс угла, изображённого на рисунке.
4. Задание 19 № 31637
Найдите тангенс угла, изображённого на рисунке.
5. Задание 19 № 32361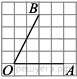 Найдите тангенс угла AOB, изображённого на
рисунке.
Найдите тангенс угла AOB, изображённого на
рисунке.
6. Задание 19 № 34018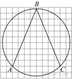
Найдите угол ABC. Ответ дайте в градусах.
7. Задание 19 № 34133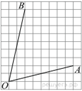
Найдите тангенс угла AOB.
8. Задание 19 № 34848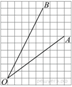
Найдите тангенс
угла ![]() .
Размер клетки 1 × 1.
.
Размер клетки 1 × 1.
9. Задание 19 № 34852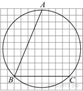
Найдите
угол ![]() .
Ответ дайте в градусах.
.
Ответ дайте в градусах.
10. Задание 19 № 3486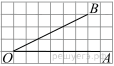
Найдите тангенс
угла ![]() ,
изображённого на рисунке.
,
изображённого на рисунке.
11. Задание 19 № 3487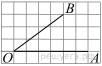
Найдите тангенс
угла ![]() ,
изображённого на рисунке.
,
изображённого на рисунке.
12. Задание 19 № 3490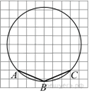
Найдите угол ABC. Ответ дайте в градусах.
13. Задание 19 № 3491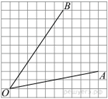
Найдите тангенс
угла ![]()
14. Задание 19 № 3492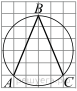
Найдите
угол ![]() .
Ответ дайте в градусах.
.
Ответ дайте в градусах.
15. Задание 19 № 3493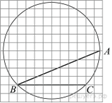
Найдите угол ABC. Ответ дайте в градусах.
16. Задание 19 № 3494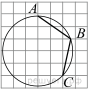
Найдите
угол ![]() .
Ответ дайте в градусах.
.
Ответ дайте в градусах.
17. Задание 19 № 3494![]()
Найдите тангенс
угла ![]() ,
изображённого на рисунке.
,
изображённого на рисунке.
18. Задание 19 № 3495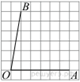
Найдите тангенс
угла ![]() ,
изображённого на рисунке.
,
изображённого на рисунке.
19. Задание 19 № 34951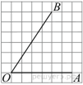
Найдите тангенс
угла ![]() ,
изображённого на рисунке.
,
изображённого на рисунке.
20. Задание 19 № 349574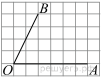
Найдите тангенс
угла ![]() ,
изображённого на рисунке.
,
изображённого на рисунке.
21. Задание 19 № 3495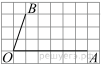
Найдите тангенс
угла ![]() ,
изображённого на рисунке.
,
изображённого на рисунке.
22. Задание 19 № 3503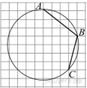
Найдите
угол ![]()
23. Задание 19 № 3506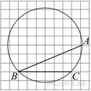
Найдите
угол ![]() .
Ответ дайте в градусах.
.
Ответ дайте в градусах.
24. Задание 19 № 3508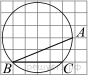
Найдите
угол ![]()
25. Задание 19 № 3509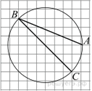
Найдите
угол ![]() .
Ответ дайте в градусах.
.
Ответ дайте в градусах.
26. Задание 19 № 3509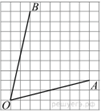
Найдите тангенс
угла ![]()
27. Задание 19 № 3513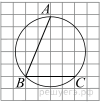
Найдите
угол ![]() .
Ответ дайте в градусах.
.
Ответ дайте в градусах.
28. Задание 19 № 3513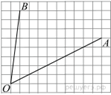 Найдите
тангенс угла
Найдите
тангенс угла ![]()
29. Задание 19 № 3514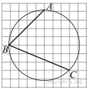 Найдите
угол ABC. Ответ дайте в градусах.
Найдите
угол ABC. Ответ дайте в градусах.
30. Задание 19 № 3516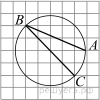 Найдите
угол
Найдите
угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
31. Задание 19 № 3520 Найдите тангенс угла
Найдите тангенс угла ![]()
32. Задание 19 № 3524 Найдите
тангенс угла
Найдите
тангенс угла ![]()
33. Задание 19 № 3528 Найдите угол
Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
34. Задание 19 № 3532 Найдите угол
Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
35. Задание 19 № 3532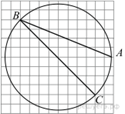 Найдите угол
Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
36. Задание 19 № 3533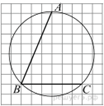 Найдите угол
Найдите угол ![]() . Ответ дайте в градусах
. Ответ дайте в градусах
37. Задание 19 № 35353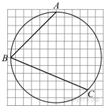 Найдите угол
Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
38. Задание 19 № 353584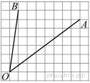 Найдите тангенс угла
Найдите тангенс угла ![]()
Расстояние от точки до прямой
1. Задание 19 № 31176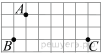 На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние
от точки А до прямой ВС. Ответ выразите в
сантиметрах.
На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние
от точки А до прямой ВС. Ответ выразите в
сантиметрах.
2. Задание 19 № 31179![]()
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
3. Задание 19 № 31181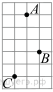 На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние
от точки А до середины отрезка ВС. Ответ выразите
в сантиметрах.
На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние
от точки А до середины отрезка ВС. Ответ выразите
в сантиметрах.
4. Задание 19 № 31185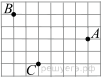 На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние
от точки А до середины отрезка ВС. Ответ выразите
в сантиметрах.
На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние
от точки А до середины отрезка ВС. Ответ выразите
в сантиметрах.
5. Задание 19 № 31628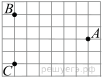 На клетчатой бумаге с размером клетки 1 см × 1
см отмечены точки А, В и С. Найдите
расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1 см × 1
см отмечены точки А, В и С. Найдите
расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.
6. Задание 19 № 316322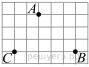
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до прямой BC. Ответ выразите в сантиметрах.
7. Задание 19 № 33941 На клетчатой бумаге с размером клетки
1 см × 1 см отмечены точки A, B и C.
Найдите расстояние от точки A до середины отрезка BC.
Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки
1 см × 1 см отмечены точки A, B и C.
Найдите расстояние от точки A до середины отрезка BC.
Ответ выразите в сантиметрах.
8. Задание 19 № 349966
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
Треугольники общего вида
1. Задание 19 № 34170 На клетчатой бумаге с размером клетки 1x1 изображён
треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.
На клетчатой бумаге с размером клетки 1x1 изображён
треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.
2. Задание 19 № 34840 На клетчатой бумаге с размером клетки 1×1 изображён
треугольник. Найдите его площадь.
На клетчатой бумаге с размером клетки 1×1 изображён
треугольник. Найдите его площадь.
3. Задание 19 № 34848 На клетчатой бумаге с размером клетки 1х1 изображён
треугольник
На клетчатой бумаге с размером клетки 1х1 изображён
треугольник ![]() . Найдите длину его средней линии, параллельной
стороне
. Найдите длину его средней линии, параллельной
стороне ![]() .
.
4. Задание 19 № 34864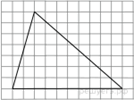
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
5. Задание 19 № 34867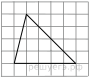
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
6. Задание 19 № 34886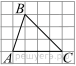
На клетчатой
бумаге с размером клетки 1х1 изображён треугольник ![]() .
Найдите длину его средней линии, параллельной стороне
.
Найдите длину его средней линии, параллельной стороне ![]()
7. Задание 19 № 34910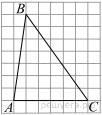
На клетчатой
бумаге с размером клетки 1х1 изображён треугольник ![]() .
Найдите длину его средней линии, параллельной стороне
.
Найдите длину его средней линии, параллельной стороне ![]() .
.
8. Задание 19 № 34911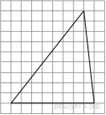
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
9. Задание 19 № 349244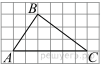
На клетчатой
бумаге с размером клетки 1х1 изображён треугольник ![]() .
Найдите длину его средней линии, параллельной стороне
.
Найдите длину его средней линии, параллельной стороне ![]() .
.
10. Задание 19 № 349561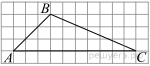
На клетчатой
бумаге с размером клетки 1х1 изображён треугольник ![]() .
Найдите длину его средней линии, параллельной стороне
.
Найдите длину его средней линии, параллельной стороне ![]() .
.
Прямоугольный треугольник
1. Задание 19 № 66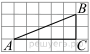 Найдите тангенс угла А треугольника ABC,
изображённого на рисунке.
Найдите тангенс угла А треугольника ABC,
изображённого на рисунке.
2. Задание 19 № 92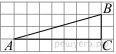 Найдите тангенс угла B треугольника ABC,
изображённого на рисунке.
Найдите тангенс угла B треугольника ABC,
изображённого на рисунке.
3. Задание 19 № 196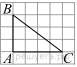 Найдите тангенс угла С треугольника ABC ,
изображённого на рисунке.
Найдите тангенс угла С треугольника ABC ,
изображённого на рисунке.
4. Задание 19 № 311491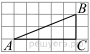
Найдите тангенс
угла ![]() треугольника
треугольника ![]() ,
изображённого на рисунке.
,
изображённого на рисунке.
5. Задание 19 № 311495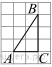 Найдите тангенс угла
Найдите тангенс угла ![]() треугольника
треугольника ![]() , изображённого на рисунке.
, изображённого на рисунке.
6. Задание 19 № 31149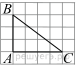 Найдите тангенс угла
Найдите тангенс угла ![]() треугольника
треугольника ![]() , изображённого на рисунке.
, изображённого на рисунке.
7. Задание 19 № 311958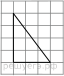
На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённой из вершины прямого угла.
8. Задание 19 № 31483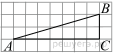 Найдите тангенс угла В треугольника ABC,
изображённого на рисунке.
Найдите тангенс угла В треугольника ABC,
изображённого на рисунке.
9. Задание 19 № 34846
На клетчатой бумаге с размером клетки 1x1 изображен прямоугольный треугольник. Найдите длину его большего катета.
10. Задание 19 № 3491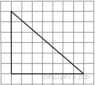
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
11. Задание 19 № 3496
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
12. Задание 19 № 35001
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
13. Задание 19 № 350062
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Параллелограмм
1. Задание 19 № 31135
На рисунке
изображен параллелограмм ![]() .
Используя рисунок, найдите
.
Используя рисунок, найдите ![]() .
.
2. Задание 19 № 31136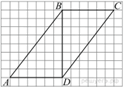
На рисунке с
размером клетки 1×1 изображен параллелограмм ![]() .
Используя рисунок, найдите
.
Используя рисунок, найдите ![]() .
.
3. Задание 19 № 31140
На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.
4. Задание 19 № 348499
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
5. Задание 19 № 34850
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
6. Задание 19 № 34975
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
7. Задание 19 № 349925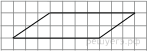
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
Ромб
1. Задание 19 № 311333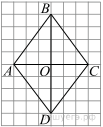
На рисунке
изображен ромб ![]() .
Используя рисунок, найдите
.
Используя рисунок, найдите ![]() .
.
2. Задание 19 № 31137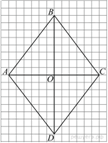
На рисунке
изображен ромб ![]() .
Используя рисунок, найдите
.
Используя рисунок, найдите ![]() .
.
3. Задание 19 № 34844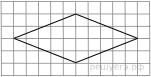 На клетчатой бумаге с размером клетки 1×1 изображён
ромб. Найдите длину его большей диагонали.
На клетчатой бумаге с размером клетки 1×1 изображён
ромб. Найдите длину его большей диагонали.
4. Задание 19 № 34858
На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите длину его большей диагонали.
5. Задание 19 № 34902
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
6. Задание 19 № 349478
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Трапеция
1. Задание 19 № 31132
На рисунке
изображена трапеция ![]() .
Используя рисунок, найдите
.
Используя рисунок, найдите ![]() .
.
2. Задание 19 № 31134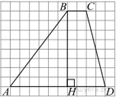
На рисунке
изображена трапеция ![]() .
Используя рисунок, найдите
.
Используя рисунок, найдите ![]() .
.
3. Задание 19 № 31138
На клетчатой бумаге с размером клетки 1см × 1см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах.
4. Задание 19 № 31191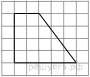
Найдите синус острого угла трапеции, изображённой на рисунке.
5. Задание 19 № 31483 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
6. Задание 19 № 34861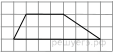
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
7. Задание 19 № 34863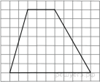
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
8. Задание 19 № 34865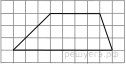
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
9. Задание 19 № 34915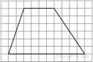
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
10. Задание 19 № 3491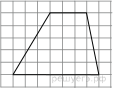
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
11. Задание 19 № 3492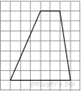
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
12. Задание 19 № 3494
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
13. Задание 19 № 3494
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
14. Задание 19 № 3494
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
15. Задание 19 № 34959
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
16. Задание 19 № 349928
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
Многоугольники
1. Задание 19 № 32375
Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
2. Задание 19 № 32379 Площадь одной клетки равна 1. Найдите площадь закрашенной
фигуры.
Площадь одной клетки равна 1. Найдите площадь закрашенной
фигуры.
3. Задание 19 № 34167 На клетчатой бумаге с размером клетки 1x1 изображена
фигура. Найдите её площадь.
На клетчатой бумаге с размером клетки 1x1 изображена
фигура. Найдите её площадь.
4. Задание 19 № 34907
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
5. Задание 19 № 349712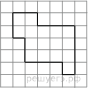
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Анализ геометрических высказываний
1. Задание 20 № 67Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Если утверждений несколько, запишите их номера в порядке возрастания.
2. Задание 20 № 93Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны. Если утверждений несколько, запишите их номера в порядке возрастания.
3. Задание 20 Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Если утверждений несколько, запишите их номера в порядке возрастания.
4. Задание 20 Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов любого треугольника равна 180° .
Если утверждений несколько, запишите их номера в порядке возрастания.
5. Задание 20 Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Если утверждений несколько, запишите их номера в порядке возрастания.
6. Задание 20 Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Если утверждений несколько, запишите их номера в порядке возрастания.
7. Задание 20 Какие из следующих утверждений верны?
1) Если угол равен 45°, то вертикальный с ним угол равен 45°.
2) Любые две прямые имеют ровно одну общую точку.
3) Через любые три точки проходит ровно одна прямая.
4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
8. Задание 20 Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
2) Любые две прямые имеют не менее одной общей точки.
3) Через любую точку проходит более одной прямой.
4) Любые три прямые имеют не менее одной общей точки.
Если утверждений несколько, запишите их номера в порядке возрастания.
9. Задание 20 Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
2) Если угол равен 60°, то смежный с ним равен 120°.
3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
4) Через любые три точки проходит не более одной прямой.
Если утверждений несколько, запишите их номера в порядке возрастания.
10. Задание 2Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°. Если утверждений несколько, запишите их номера в порядке возрастания.
11. Задание 20 № Какие из следующих утверждений верны?
1) Через любые три точки проходит не более одной окружности.
2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.
3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.
4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.
Если утверждений несколько, запишите их номера в порядке возрастания.
12. Задание 20 № Какие из следующих утверждений верны?
1) Сумма углов выпуклого четырехугольника равна 180°.
2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.
3) Диагонали квадрата делят его углы пополам.
4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
Если утверждений несколько, запишите их номера в порядке возрастания.
13. Задание 20 № Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°. Если утверждений несколько, запишите их номера в порядке возрастания.
14. Задание 20 № Какие из следующих утверждений верны?
1) Около всякого треугольника можно описать не более одной окружности.
2) В любой треугольник можно вписать не менее одной окружности.
3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
Если утверждений несколько, запишите их номера в порядке возрастания.
15. Задание 20 № Какие из следующих утверждений верны?
) Около любого правильного многоугольника можно описать не более одной окружности.
2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.
3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.
4) Около любого ромба можно описать окружность.
сли утверждений несколько, запишите их номера в порядке возрастания.
16. Задание 20 № Какие из следующих утверждений верны?
1) Окружность имеет бесконечно много центров симметрии.
2) Прямая не имеет осей симметрии.
3) Правильный пятиугольник имеет пять осей симметрии.
4) Квадрат не имеет центра симметрии.
Если утверждений несколько, запишите их номера в порядке возрастания.
17. Задание 20 № Какие из следующих утверждений верны?
1) Правильный шестиугольник имеет шесть осей симметрии.
2) Прямая не имеет осей симметрии.
3) Центром симметрии ромба является точка пересечения его диагоналей.
4) Равнобедренный треугольник имеет три оси симметрии.
Если утверждений несколько, запишите их номера в порядке возрастания.
18. Задание 20 № Какие из следующих утверждений верны?
1) Центром симметрии прямоугольника является точка пересечения диагоналей.
2) Центром симметрии ромба является точка пересечения его диагоналей.
3) Правильный пятиугольник имеет пять осей симметрии.
4) Центром симметрии равнобедренной трапеции является точка пересечения ее диагоналей.
Если утверждений несколько, запишите их номера в порядке возрастания.
19. Задание 20 № Какие из следующих утверждений верны?
1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
2) Любые два равнобедренных треугольника подобны.
3) Любые два прямоугольных треугольника подобны.
4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Задание 20 № Какие из следующих утверждений верны?
1) Любые два прямоугольных треугольника подобны.
2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
3) Стороны треугольника пропорциональны косинусам противолежащих углов.
4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Если утверждений несколько, запишите их номера в порядке возрастания.
21. Задание 20 № Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета. Если утверждений несколько, запишите их номера в порядке возрастания.
22. Задание 20акие из следующих утверждений верны?
1) Если площади фигур равны, то равны и сами фигуры.
2) Площадь трапеции равна произведению суммы оснований на высоту.
3) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
4) Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10.
Если утверждений несколько, запишите их номера в порядке возрастания.
23. Задание 20Какие из следующих утверждений верны?
1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
3) Площадь трапеции меньше произведения суммы оснований на высоту.
4) Площадь прямоугольного треугольника меньше произведения его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
24. Задание 20Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
Если утверждений несколько, запишите их номера в порядке возрастания.
25. Задание 20Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
Если утверждений несколько, запишите их номера в порядке возрастания.
26. Задание 20Укажите номера верных утверждений.
1) Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.
2) Через любые три точки проходит не более одной прямой.
3) Сумма вертикальных углов равна 180°.
Если утверждений несколько, запишите их номера в порядке возрастания.
27. Задание 20Укажите номера верных утверждений.
1) Площадь трапеции равна половине высоты, умноженной на разность оснований.
2) Через любые две точки можно провести прямую.
3) Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.
Если утверждений несколько, запишите их номера в порядке возрастания.
28. Задание 20Укажите номера верных утверждений.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
29. Задание 20Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
Если утверждений несколько, запишите их номера в порядке возрастания.
30. Задание 20Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
31. Задание 20Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
Если утверждений несколько, запишите их номера в порядке возрастания.
32. Задание 20Укажите номера верных утверждений.
1) Смежные углы равны.
2) Любые две прямые имеют ровно одну общую точку.
3) Если угол равен 108°, то вертикальный с ним равен 108°.
Если утверждений несколько, запишите их номера в порядке возрастания.
33. Задание 20Укажите номера верных утверждений.
1) Если угол равен 47°, то смежный с ним равен 153°.
2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Через любую точку проходит ровно одна прямая.
Если утверждений несколько, запишите их номера в порядке возрастания.
34. Задание 20Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.
Если утверждений несколько, запишите их номера в порядке возрастания.
35. Задание 20Укажите номера неверных утверждений.
1) При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.
2) Диагонали ромба перпендикулярны.
3) Центром окружности, описанной около треугольника, является точка пересечения его биссектрис. Если утверждний несколько, запишите их номера в порядке возрастания.
36. Задание 20 №Какое из следующих утверждений верно?
1) Диагонали параллелограмма равны.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
37. Задание 20 №Какие из следующих утверждений верны?
1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2) В тупоугольном треугольнике все углы тупые.
3) Средняя линия трапеции равна полусумме её оснований.
Если утверждений несколько, запишите их номера в порядке возрастания.
38. Задание 20 №Какие из следующих утверждений верны?
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Средняя линия трапеции параллельна её основаниям.
3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
39. Задание 20 №Какое из следующих утверждений верно?
1) Точка касания двух окружностей равноудалена от центров этих окружностей.
2) В параллелограмме есть два равных угла.
3) Площадь прямоугольного треугольника равна произведению длин его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
40. Задание 20 №Какие из следующих утверждений верны?
1) Один из углов треугольника всегда не превышает 60 градусов.
2) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
41. Задание 20 №Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Сумма углов любого треугольника равна 360 градусам.
3) Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности. Если утверждений несколько, запишите их номера в порядке возрастания.
42. Задание 20 №Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
43. Задание 20 Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Смежные углы равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
4. Задание 20 №Какое из следующих утверждений верно?
1. Все углы ромба равны.
2. Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности. В ответ запишите номер выбранного утверждения.
Алгебраические выражения
1. Задание 21 № 47Сократите дробь ![]() .
.
2. Задание 21 № 311236Разложите на множители: ![]() .
.
3. Задание 21 № 311243Сократите дробь ![]()
4. Задание 21 № 311255Упростите выражение 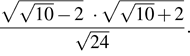
5. Задание 21 № 311552Один из корней уравнения ![]() равен 1. Найдите второй корень.
равен 1. Найдите второй корень.
6. Задание 21 № 311575Упростите выражение: ![]() .
.
7. Задание 21 № 311579Упростите выражение: ![]() .
.
8. Задание 21 № 311582Упростите выражение: ![]() .
.
9. Задание 21 № 311584Упростите выражение: ![]()
10. Задание 21 № 31158Найдите значение выражения: ![]() при
при ![]()
11. Задание 21 № 31159Сократите дробь: ![]()
12. Задание 21 № 31159Какое из чисел больше: ![]() или
или ![]() ?
?
13. Задание 21 № 31165Сократите дробь ![]() , если
, если ![]() .
.
14. Задание 21 № 311921Упростите выражение ![]()
15. Задание 21 № 311965Сократите дробь ![]()
16. Задание 21 № 314310Сократите дробь ![]()
17. Задание 21 № 314410Сократите дробь ![]()
18. Задание 21 № 31854айдите значение выражения ![]() при
при ![]()
![]() В ответе запишите найденное значение.
В ответе запишите найденное значение.
19. Задание 21 № 338112Найдите значение выражения ![]() если
если ![]()
20. Задание 21 № 338134Найдите значение выражения ![]() если
если ![]()
21. Задание 21 № 338222Найдите значение выражения ![]() если
если ![]()
22. Задание 21 № 340876Найдите значение выражения ![]() при
при ![]()
23. Задание 21 № 340931Сократите дробь ![]()
24. Задание 21 № 341533Сократите дробь ![]()
25. Задание 21 № 352715Сократите дробь ![]()
26. Задание 21 № 353431Найдите значение выражения ![]() если
если ![]()
Уравнения
1. Задание 21 № 311546Один из корней уравнения ![]() равен
равен ![]() . Найдите второй корень.
. Найдите второй корень.
2. Задание 21 № 311586Решите уравнение: ![]()
3. Задание 21 № 311587Решите уравнение: ![]()
4. Задание 21 № 311589Решите уравнение: ![]()
5. Задание 21 № 311591Решите уравнение: ![]()
6. Задание 21 № 311618Решите уравнение ![]() .
.
7. Задание 21 № 338053Решите уравнение ![]()
8. Задание 21 № 338070Решите уравнение ![]()
9. Задание 21 № 338079Решите уравнение ![]()
10. Задание 21 № 33808Решите уравнение ![]()
11. Задание 21 № 33817Решите уравнение ![]()
12. Задание 21 № 33849Решите уравнение ![]()
13. Задание 21 № 33852Решите уравнение ![]()
14. Задание 21 № 33859Решите уравнение ![]()
15. Задание 21 № 33863Решите уравнение ![]()
16. Задание 21 № 33866Решите уравнение ![]()
17. Задание 21 № 33875Решите уравнение ![]()
18. Задание 21 № 33885Решите уравнение ![]()
19. Задание 21 № 33886Решите уравнение ![]()
20. Задание 21 № 33895Решите уравнение ![]()
21. Задание 21 № 33899Решите уравнение ![]()
22. Задание 21 № 339026Решите уравнение ![]()
23. Задание 21 № 340902Решите уравнение ![]()
24. Задание 21 № 341507Решите уравнение x6 = (6x − 8)3.
25. Задание 21 № 353542Решите уравнение ![]()
Неравенства
1. Задание 21 № 125ешите неравенство ![]()
2. Задание 21 № 177Решите неравенство ![]()
3. Задание 21 № 311237Решите неравенство ![]() .
.
4. Задание 21 № 314563Решите неравенство ![]()
5. Задание 21 № 314574Решите неравенство ![]()
6. Задание 21 № 314576Решите неравенство ![]()
7. Задание 21 № 314582Решите неравенство ![]()
8. Задание 21 № 314594Решите неравенство ![]()
9. Задание 21 № 333318Решите неравенство ![]()
10. Задание 21 № 33850Решите неравенство ![]()
11. Задание 21 № 33851Решите неравенство ![]()
12. Задание 21 № 33856Решите неравенство ![]()
13. Задание 21 № 33870Решите неравенство ![]()
14. Задание 21 № 33894Решите неравенство ![]()
15. Задание 21 № 340850Решите неравенство ![]()
16. Задание 21 № 353573Решите неравенство ![]()
Системы уравнений
1. Задание 21 № 73Решите систему уравнений 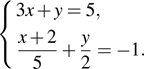
2. Задание 21 № 99Решите систему уравнений 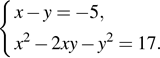
3. Задание 21 № 311585Решите систему уравнений: 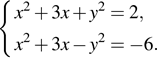
4. Задание 21 № 31635Решите систему уравнений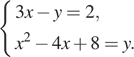
5. Задание 21 № 333022ешите систему 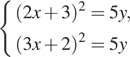
6. Задание 21 № 338528Решите систему уравнений 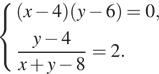
7. Задание 21 № 338545Решите систему уравнений 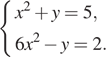
8. Задание 21 № 338650Решите систему уравнений 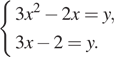
9. Задание 21 № 338707Решите систему уравнений 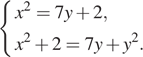
10. Задание 21 № 338894Решите систему уравнений 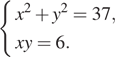
11. Задание 21 № 341282Решите систему уравнений 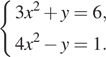
12. Задание 21 № 341340Решите систему уравнений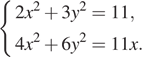
13. Задание 21 № 341366ешите систему уравнений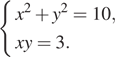
14. Задание 21 № 353393Решите систему уравнений: 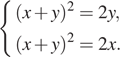
Системы неравенств
1. Задание 21 № 338522Решите систему неравенств 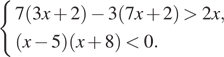
2. Задание 21 № 338633Решите систему неравенств 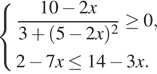
3. Задание 21 № 341392Решите систему неравенств 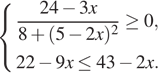
4. Задание 21 № 341418Решите систему неравенств
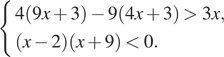
5. Задание 21 № 353544Решите систему неравенств 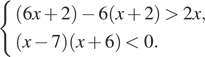
Задачи на проценты, сплавы и смеси
1. Задание 22 № 311653Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
2. Задание 22 № 314395Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
3. Задание 22 № 314431При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
4. Задание 22 № 314508На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?
5. Задание 22 № 316357Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
6. Задание 22 № 338773Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
7. Задание 22 № 338786Смешали некоторое количество 10-процентного раствора некоторого вещества с таким же количеством 12-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
8. Задание 22 № 341367Свежие фрукты содержат 86 % воды, а высушенные — 23 %. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?
9. Задание 22 № 348438Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
10. Задание 22 № 349497Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе?
11. Задание 22 № 349691Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором растворе?
12. Задание 22 № 349700Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом растворе?
13. Задание 22 № 349844Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
14. Задание 22 № 350150Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?
15. Задание 22 № 350236Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором растворе?
16. Задание 22 № 351603Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты содержится в первом растворе?
17. Задание 22 № 351824Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37% кислоты. Сколько килограммов кислоты содержится во втором растворе?
18. Задание 22 № 352466Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
19. Задание 22 № 353507Свежие фрукты содержат 88 % воды, а высушенные — 30 %. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов?
20. Задание 22 № 353527Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
21. Задание 22 № 353545Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько сухих фруктов получится из 252 кг свежих фруктов?
Движение по прямой
1. Задание 22 № 126Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от А. Найдите скорость пешехода, шедшего из А, если известно, что он шёл со скоростью, на 1 км/ч большей, чем пешеход, шедший из В, и сделал в пути получасовую остановку.
2. Задание 22 № 178Из пункта А в пункт В, расстояние между которыми 19 км, вышел пешеход. Через полчаса навстречу ему из пункта В вышел турист и встретил пешехода в 9 км от В. Турист шёл со скоростью, на 1 км/ч большей, чем пешеход. Найдите скорость пешехода, шедшего из А.
3. Задание 22 № 311558Расстояние между городами А и В равно 375 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 1 час 30 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С.
4. Задание 22 № 311600Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
5. Задание 22 № 311601Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
6. Задание 22 № 311615Железнодорожный состав длиной в 1 км прошёл бы мимо столба за 1 мин., а через туннель (от входа локомотива до выхода последнего вагона) при той же скорости — за 3 мин. Какова длина туннеля (в км)?
7. Задание 22 № 314507Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
8. Задание 22 № 314559Из пункта А в пункт В, расстояние между которыми 27 км, вышел турист. Через полчаса навстречу ему из пункта В вышел пешеход и встретил туриста в 12 км от А. Найдите скорость туриста, если известно, что она была на 2 км/ч меньше скорости пешехода.
9. Задание 22 № 314593Из пункта А в пункт В, расстояние между которыми 34 км, выехал велосипедист. Одновременно с ним из В в А вышел пешеход. Велосипедист ехал со скоростью, на 8 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость велосипедиста, если известно, что они встретились в 10 км от пункта В.
10. Задание 22 № 5Из пункта А в пункт В, расстояние между которыми 19 км, вышел пешеход. Через полчаса навстречу ему из пункта В вышел турист и встретил пешехода в 9 км от В. Турист шёл со скоростью, на 1 км/ч большей, чем пешеход. Найдите скорость пешехода, шедшего из А.
11. Задание 22 № 333023Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 3 км/ч пешехода за 57 секунд. Найдите длину поезда в метрах.
12. Задание 22 № 333102Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 45 секунд. Найдите длину поезда в метрах.
13. ЗаданИз двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 30 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 144 км, скорость первого велосипедиста равна 24 км/ч, скорость второго — 28 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
14. Задание 22 № 338510Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
15. Задание 22 № 338552Первый велосипедист выехал из посёлка по шоссе со скоростью 18 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 4 часа после этого догнал первого.
16. Задание 22 № 338561Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 11 км/ч, а вторую половину пути проехал со скоростью 66 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.
17. Задание 2Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 40 минут раньше, чем велосипедист приехал в А, а встретились они через 15 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?
18. Задание 22 № 338603Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
19. Задание 22 № 338669Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 48 минут раньше, чем велосипедист приехал в А, а встретились они через 18 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?
20. Задание 22 № 67Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, скорость второго — 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
21. Задание 22 № 338904Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.
22. Задание 22 № 338919Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
23. Задание 22 № 338945Расстояние между городами А и В равно 120 км. Из города А в город В выехал автомобиль, а через 90 минут следом за ним со скоростью 100 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.
24. Задание 22 №Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
25. Задание 22 № 338972Два автомобиля одновременно отправляются в 240-километровый пробег. Первый едет со скоростью на 20 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
26. Задание 22 № 3992Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 60 км. Отдохнув, он отправился обратно в А, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
27. Задание 22 №Дорога между пунктами A и В состоит из подъёма и спуска, а её длина равна 14 км. Турист прошёл путь из А в В за 4 часа, из которых спуск занял 2 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 3 км/ч?
28. Задание 22 № 3Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 4 км от места отправления. Один идёт со скоростью 2,7 км/ч, а другой — со скоростью 4,5 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
29. Задание 22 № 341283Поезд, двигаясь равномерно со скоростью 86 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 18 секунд. Найдите длину поезда в метрах.
30. Задание 22 № 341288Поезд, двигаясь равномерно со скоростью 44 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 4 км/ч, за 81 секунду. Найдите длину поезда в метрах.
31. Задание 22 № 341393Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 3 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 9 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.
32. Задание 22 №Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 30 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на 9 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
33. Задание 22 № 3Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 57 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на 38 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
34. Задание 22 № 352780Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 33 минуты раньше, чем велосипедист приехал в А, а встретились они через 22 минуты после выезда. Сколько часов затратил на путь из В в А велосипедист?
35. Задание 22 № 3522Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 100 км. Отдохнув, он отправился обратно в А, увеличив скорость на 15 км/ч. По пути он сделал остановку на 6 часов, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
36. Задание 22 № 5Дорога между пунктами A и В состоит из подъёма и спуска, а её длина равна 27 км. Турист прошёл путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?
37. Задание 22 № 353092Расстояние между городами А и В равно 120 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 36 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из C в А, автомобиль прибыл в В. Найдите расстояние от А до С.
38. Задание 22 № 353275Два велосипедиста одновременно отправляются в 180-километровый пробег. Первый едет со скоростью на 5 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.
39. Задание 22 № 353302Первый велосипедист выехал из посёлка по шоссе со скоростью 21 км/ч. Через час после него со скоростью 15 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.
40. Задание 22 № 353530Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 15 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.
41. Задание 22 № 35Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3,7 км от места отправления. Один идёт со скоростью 3,3 км/ч, а другой — со скоростью 4,1 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
42. Задание 22 № 353551Два автомобиля одновременно отправляются в 420-километровый пробег. Первый едет со скоростью, на 24 км/ч большей, чем второй, и прибывает к финишу на 2 ч раньше второго. Найдите скорость первого автомобиля.
43. Задание 22 № 353554Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 6 км/ч пешехода за 8 секунд. Найдите длину поезда в метрах.
Задачи на движение по воде
1. Задание 22 № 311245Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?
2. Задание 22 № 311564Расстояние между пристанями А и В равно 80 км. Из А в В по течению реки отправился плот, а через 2 часа вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 22 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
3. Задание 22 № 311570Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 34 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
4. Задание 22 № 311621Моторная лодка прошла 36 км по течению реки и вернулась обратно, потратив на весь путь 5 часов. Скорость течения реки равна 3 км/ч. Найдите скорость лодки в неподвижной воде.
5. Задание 22 № 311659Пристани ![]() и
и ![]() расположены на реке, скорость течения которой
на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок
со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
расположены на реке, скорость течения которой
на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок
со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
6. Задание 22 № 311693Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отдалился, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
7. Задание 22 № 314487Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 2 часа, вернулись обратно через 6 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?
8. Задание 22 № 314488Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
9. Задание 22 Катер прошёл от одной пристани до другой, расстояние
между которыми по реке равно 48 км, сделал стоянку на 20 мин и вернулся
обратно через ![]() после начала поездки. Найдите скорость течения
реки, если известно, что скорость катера в стоячей воде равна 20 км/ч.
после начала поездки. Найдите скорость течения
реки, если известно, что скорость катера в стоячей воде равна 20 км/ч.
10. Задание 22 № 314600Моторная лодка прошла от одной пристани до другой,
расстояние между которыми по реке равно 16 км, сделала стоянку на 40
мин и вернулась обратно через ![]() после начала поездки. Найдите скорость течения
реки, если известно, что скорость моторной лодки в стоячей воде равна 12
км/ч.
после начала поездки. Найдите скорость течения
реки, если известно, что скорость моторной лодки в стоячей воде равна 12
км/ч.
11. Задание 22 № 338582Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
12. Задание 22 № 338585Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
13. Задание 22 № 338967От пристани А к пристани В, расстояние между которыми равно 70 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью, на 8 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.
14. Задание 22 № 338995Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?
15. Задание 22 № 341341Расстояние между пристанями А и В равно 99 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 22 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч.
16. Задание 22 № 341419Расстояние между пристанями А и В равно 75 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 44 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
17. Задание 22 № 341534Теплоход проходит по течению реки до пункта назначения 76 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20 часов после отплытия из него.
18. Задание 22 № 352588От пристани А к пристани В, расстояние между которыми равно 153 км, отправился с постоянной скоростью первый теплоход, а через 4 часа после этого следом за ним, со скоростью, на 16 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.
19. Задание 22 № 352844Теплоход проходит по течению реки до пункта назначения 285 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 34 км/ч, стоянка длится 19 часов, а в пункт отправления теплоход возвращается через 36 часов после отплытия из него.
20. Задание 22 № 353102Баржа прошла по течению реки 48 км и, повернув обратно, прошла ещё 36 км, затратив на весь путь 6 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
21. Задание 22 № 353294Теплоход проходит по течению реки до пункта назначения 280 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 15 часов, а в пункт отправления теплоход возвращается через 39 часов после отплытия из него.
22. Задание 22 № 353433Расстояние между пристанями А и В равно 63 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 20 км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Задачи на совместную работу
1. Задание 22 № 311580Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
2. Задание 22 № 311616На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
3. Задание 22 № 311617Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
4. Задание 22 № 311770Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
5. Задание 22 № 311858Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 час. За сколько часов наполняет бассейн одна вторая труба?
6. Задание 22 № 316Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объёмом 136 литров?
7. Задание 22 № 316241Две трубы наполняют бассейн за 6 часов 18 минут, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?
8. Задание 22 № 338660Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
9. Задание 22 № 338712Три бригады изготовили вместе 266 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
10. Задание 22 Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько часов мальчики покрасят забор, работая втроём?
11. Задание 22 № 340Три бригады вместе изготовили 114 карданных валов. Известно, что вторая бригада изготовила карданных валов в 3 раза больше, чем первая, и на 16 карданных валов меньше, чем третья. На сколько карданных валов больше изготовила третья бригада, чем первая?
12. Задание 22 № 340877Три бригады изготовили вместе 114 деталей. Известно, что вторая бригада изготовила деталей в 3 раза больше, чем первая, и на 16 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
13. Задание 22 № 340903Три бригады вместе изготовили 114 синхронизаторов передач. Известно, что вторая бригада изготовила синхронизаторов в 3 раза больше, чем первая, и на 16 синхронизаторов меньше, чем третья. На сколько синхронизаторов передач больше изготовила третья бригада, чем первая.
14. Задание 22 № 352446Игорь и Паша красят забор за 18 часов. Паша и Володя красят этот же забор за 20 часов, а Володя и Игорь — за 30 часов. За сколько минут мальчики покрасят забор, работая втроём?
15. Задание 22 № 352832Три бригады изготовили вместе 248 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
16. Задание 22 № 353479Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Разные задачи
1. Задание 22 № 311652Из пяти следующих утверждений о результатах матча хоккейных команд "Транспортир" и "Линейка" четыре истинны, а одно — ложно. Определите, с каким счетом закончился матч, и укажите победителя (если матч завершился победой одной из команд). Ответ обоснуйте.
1) Выиграл "Транспортир". 2) Всего в матче было заброшено менее 10 шайб.
3) Матч закончился вничью. 4) Всего в матче было заброшено более 8 шайб.
5) "Линейка" забросила более 3 шайб.
2. Задание 22 № 311656Найдите целое число, если из двух следующих утверждений
верно только одно: 1) ![]() ; 2)
; 2) ![]() .
.
3. Задание 22 № 311657Найдите целое число, если из двух следующих утверждений
верно только одно: 1) ![]() ; 2)
; 2) ![]() .
.
4. Задание 22 № 311658Кролик утверждает, что вчера Винни-Пух съел не менее 9 баночек мёда, Пятачок — что не менее 8 баночек, ослик Иа — что не менее 7. Сколько баночек мёда съел вчера Винни-Пух, если из трех этих утверждений истинно только одно?
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.