Муниципальное общеобразовательное  бюджетное учреждение

«Средняя общеобразовательная школа №53»

РАБОЧАЯ ПРОГРАММА

Геометрия

7 - 9 классы

на 2016 – 2019 уч.год

Разработана

учителем  математики

Акимовой  Светланой Алексеевной

2016 г.

г. Оренбург

Содержание

1           Пояснительная записка

Рабочая программа  по дисциплине «Математика» составлена  для обучения указанному предмету  учащихся 5 – 6 - х классов общеобразовательных учебных учреждений. При составлении рабочей программы были использованы:

·  Федеральный закон Российской Федерации от 29 декабря 2012г. N273-ФЗ "Об образовании в Российской Федерации".

·  Федеральный государственный образовательный стандарт основного общего образования, утвержденный приказом Министерства образования и науки РФ от 17 декабря 2010г. №1897(в ред. От 29.12.2015 №1577) "Об утверждении федерального государственного образовательного стандарта основного общего образования".

·  Приказ Министерства образования и науки РФ от 29.12.2014г. N1644 "О внесении изменений в приказ Министерства образования и науки РФ от 17.12.2010г. N1897 "Об утверждении ФГОС основного общего образования"

·  Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки РФ к использованию в образовательном процессе в общеобразовательных школах на 2015-2016 учебный год

·  Примерная основная образовательная программа основного общего образования. Одобрена

решением федерального учебно-методического объединения по общему образованию (протокол от 8 апреля 2015 г. № 1/15)

• Программы. Геометрия. Сборник рабочих программ. 7-9 классы : пособие для учителей общеобраз. Учреждений/ составитель Т.А. Бурмистрова.-М.: Просвещение, 2011.-95 с.

Обучение геометрии в основной школе направлено на достижение следующих целей:

·           овладение системой математических знаний и умений, необходимых для            применения в практической деятельности, изучения смежных дисциплин,   продолжения образования;

·           интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

·           формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

·           воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

        На протяжении изучения материала предполагается закрепление и отработка основных умений и навыков, их совершенствование, а также систематизация полученных ранее знание, таким образом, системно-деятельностный подход ставит своей задачей ориентировать ученика не только на усвоение знаний, но, в первую очередь, на способы этого усвоения, на способы мышления и деятельности, на развитие познавательных сил и творческого потенциала ребенка. В связи с этим, во время учебных занятий учащихся необходимо вовлекать в различные виды деятельности (беседа, дискуссия, экскурсия, творческая работа, исследовательская (проектная) работа и другие), которые обеспечивали бы высокое качество знаний, развитие умственных и творческих способностей, познавательной, а главное самостоятельной деятельности учеников.

Данная программа направлена на формирование личностных, метапредметных и преметных результатов.

В учебном плане образовательного учреждения на освоение данного предмета отводится 204 часа.

        Преподавание ведется по первому варианту – 2 часа в неделю, всего 68 часов.

2               Планируемые результаты изучения учебного предмета, курса

Обучающийся научится в 7 классе (для использования в повседневной жизни и обеспечения возможности успешного продолжения образования на базовом уровне)

Геометрические фигуры

·           Оперировать на базовом уровне понятиями геометрических фигур;

·           извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде;

·           применять для решения задач геометрические факты, если условия их применения заданы в явной форме;

·           решать задачи на нахождение геометрических величин по образцам или алгоритмам.

В повседневной жизни и при изучении других предметов:

·           использовать свойства геометрических фигур для решения типовых задач, возникающих в ситуациях повседневной жизни, задач практического содержания.

Отношения

·           Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция.

В повседневной жизни и при изучении других предметов:

·           использовать отношения для решения простейших задач, возникающих в реальной жизни.

Измерения и вычисления

·           Выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;

В повседневной жизни и при изучении других предметов:

·           вычислять расстояния на местности в стандартных ситуациях.

Геометрические построения

·           Изображать типовые плоские фигуры и фигуры в пространстве от руки и с помощью инструментов.

В повседневной жизни и при изучении других предметов:

·           выполнять простейшие построения на местности, необходимые в реальной жизни.

История математики

·           Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;

·           знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;

·           понимать роль математики в развитии России.

Методы математики

·           Выбирать подходящий изученный метод для решения изученных типов математических задач;

·           приводить примеры математических закономерностей в окружающей действительности и произведениях искусства.

Обучающийся получит возможность научиться в 7 классе для обеспечения возможности успешного продолжения образования на базовом и углублённом уровнях

Геометрические фигуры

·           Оперировать понятиями геометрических фигур;

·           извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;

·           применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения;

·           формулировать в простейших случаях свойства и признаки фигур;

·           доказывать геометрические утверждения;

·           владеть стандартной классификацией плоских фигур (треугольников).

В повседневной жизни и при изучении других предметов:

·           использовать свойства геометрических фигур для решения задач практического характера и задач из смежных дисциплин.

Отношения

·           Оперировать понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция.

В повседневной жизни и при изучении других предметов:

·           использовать отношения для решения задач, возникающих в реальной жизни.

Измерения и вычисления

·           Оперировать представлениями о длине;

·           формулировать задачи на вычисление длин.

В повседневной жизни и при изучении других предметов:

·           проводить вычисления на местности;

·           применять формулы при вычислениях в смежных учебных предметах, в окружающей действительности.

Геометрические построения

·           Изображать геометрические фигуры по текстовому и символьному описанию;

·           свободно оперировать чертёжными инструментами в несложных случаях,

·           выполнять построения треугольников, применять отдельные методы построений циркулем и линейкой и проводить простейшие исследования числа решений;

·           изображать типовые плоские фигуры с помощью простейших компьютерных инструментов.

В повседневной жизни и при изучении других предметов:

·           выполнять простейшие построения на местности, необходимые в реальной жизни;

·           оценивать размеры реальных объектов окружающего мира.

В повседневной жизни и при изучении других предметов:

·           применять свойства движений и применять подобие для построений и вычислений.

История математики

·           Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;

·           понимать роль математики в развитии России.

Методы математики

·           Используя изученные методы, проводить доказательство, выполнять опровержение;

·           выбирать изученные методы и их комбинации для решения математических задач;

·           использовать математические знания для описания закономерностей в окружающей действительности и произведениях искусства;

·           применять простейшие программные средства и электронно-коммуникационные системы при решении математических задач.

                 Программа обеспечивает достижения следующих результатов освоения образовательной программы основного общего образования:

Личностные результаты освоения основной образовательной программы:

·         воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;

·         ответственное отношение к учению, готовность и спо­собность обучающихся к саморазвитию и самообразова­нию на основе мотивации к обучению и познанию;

·         осознанный выбор и построение дальнейшей индивиду­альной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а так­же на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;

·         сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики, учитывающего социальное, культурное, языковое, духовное многообразие современного мира.

·         осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению, мировоззрению, культуре, языку, вере, гражданской позиции;

·         умение контролировать процесс и результат учебной и математической деятельности;

·         критичность мышления, инициатива, находчивость, активность при решении математических задач.

Метапредметные результаты освоения основной образовательной программы:

Регулятивные УУД:

·         самостоятельно определять цели обучения, ставить и формулировать новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности;

·         самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

·         соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;

·         оценивать правильность выполнения учебной задачи, собственные возможности ее решения;

·         владеть основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности;

·         составлять (индивидуально или в группе) план решения проблемы;

·         умение осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы.

Познавательные УУД:

• определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное, по аналогии) и делать выводы;
• создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач;
• находить в тексте требуемую информацию (в соответствии с целями своей деятельности); уметь определять возможные источники необходимых сведений, производить поиск информации, анализировать и оценивать её достоверность;
•  осуществлять сравнение и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций;
• создавать математические модели;
• составлять тезисы, различные виды планов (простых, сложных и т.п.);п
• преобразовывать информацию из одного вида в другой ;
• понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания;
• самому создавать источники информации разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности;

·         использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей; умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;

·         выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

·         применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.

Коммуникативные УУД:

• организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; формулировать, аргументировать и отстаивать свое мнение;
• отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами;
• в дискуссии уметь выдвинуть контраргументы;
•  учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения и корректировать его;
• понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;
• уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций;

• умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.

Предметные результаты освоения основной образовательной программы:

• овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (геометрическая фигура, величина) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
• умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
• овладение навыками устных письменных, инструментальных вычислений;
• овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
• усвоение систематических знаний о плоских фигурах и их свойствах, умение применять систематические знания о них для решения геометрических и практических задач;
• умение измерять длины отрезков, величины углов;
• умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочные материалы и технические средства.

Обучающийся научится в 8 классе (для использования в повседневной жизни и обеспечения возможности успешного продолжения образования на базовом уровне)

Геометрические фигуры

·           Оперировать на базовом уровне понятиями геометрических фигур;

·           извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде;

·           применять для решения задач геометрические факты, если условия их применения заданы в явной форме;

·           решать задачи на нахождение геометрических величин по образцам или алгоритмам.

В повседневной жизни и при изучении других предметов:

·           использовать свойства геометрических фигур для решения типовых задач, возникающих в ситуациях повседневной жизни, задач практического содержания.

Отношения

·           Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры, равенство треугольников.

В повседневной жизни и при изучении других предметов:

·           использовать отношения для решения простейших задач, возникающих в реальной жизни.

Измерения и вычисления

·           Применять формулы периметра, площади и объёма, площади поверхности отдельных многогранников при вычислениях, когда все данные имеются в условии;

·           применять теорему Пифагора, базовые тригонометрические соотношения для вычисления длин, расстояний, площадей в простейших случаях.

В повседневной жизни и при изучении других предметов:

·           вычислять расстояния на местности в стандартных ситуациях, площади в простейших случаях, применять формулы в простейших ситуациях в повседневной жизни.

Геометрические построения

·           Изображать типовые плоские фигуры и фигуры в пространстве от руки и с помощью инструментов.

В повседневной жизни и при изучении других предметов:

·           выполнять простейшие построения на местности, необходимые в реальной жизни.

Геометрические преобразования

·           Строить фигуру, симметричную данной фигуре относительно оси и точки.

В повседневной жизни и при изучении других предметов:

·           распознавать движение объектов в окружающем мире;

·           распознавать симметричные фигуры в окружающем мире.

История математики

·           Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;

·           знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;

·           понимать роль математики в развитии России.

Методы математики

·           Выбирать подходящий изученный метод для решении изученных типов математических задач;

·           Приводить примеры математических закономерностей в окружающей действительности и произведениях искусства.

Обучающийся получит возможность научиться в 8 классе для обеспечения возможности успешного продолжения образования на базовом и углублённом уровнях

Геометрические фигуры

·           Оперировать понятиями геометрических фигур;

·           извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;

·           применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения;

·           формулировать в простейших случаях свойства и признаки фигур;

·           доказывать геометрические утверждения;

·           владеть стандартной классификацией плоских фигур (четырёхугольников).

В повседневной жизни и при изучении других предметов:

·           использовать свойства геометрических фигур для решения задач практического характера и задач из смежных дисциплин.

Отношения

·           Оперировать понятиями: подобие фигур, подобные фигуры, подобные треугольники;

·           применять теорему Фалеса и теорему о пропорциональных отрезках при решении задач;

·           характеризовать взаимное расположение прямой и окружности, двух окружностей.

В повседневной жизни и при изучении других предметов:

·           использовать отношения для решения задач, возникающих в реальной жизни.

Измерения и вычисления

·           Оперировать представлениями о длине, площади как величинами. Применять теорему Пифагора, формулы площади, объёма при решении многошаговых задач, в которых не все данные представлены явно, а требуют вычислений, оперировать более широким количеством формул длины, площади, объёма, вычислять характеристики комбинаций фигур (окружностей и многоугольников) вычислять расстояния между фигурами, применять тригонометрические формулы для вычислений в более сложных случаях, проводить вычисления на основе равновеликости и равносоставленности;

·           формулировать задачи на вычисление длин, площадей и решать их.

В повседневной жизни и при изучении других предметов:

·           проводить вычисления на местности;

·           применять формулы при вычислениях в смежных учебных предметах, в окружающей действительности.

Геометрические построения

·           Изображать геометрические фигуры по текстовому и символьному описанию;

·           свободно оперировать чертёжными инструментами в несложных случаях,

·           выполнять построения треугольников, применять отдельные методы построений циркулем и линейкой и проводить простейшие исследования числа решений;

·           изображать типовые плоские фигуры и объемные тела с помощью простейших компьютерных инструментов.

В повседневной жизни и при изучении других предметов:

·           выполнять простейшие построения на местности, необходимые в реальной жизни;

·           оценивать размеры реальных объектов окружающего мира.

Преобразования

·           Оперировать понятием движения и преобразования подобия, владеть приёмами построения фигур с использованием движений и преобразований подобия, применять полученные знания и опыт построений в смежных предметах и в реальных ситуациях окружающего мира;

·           строить фигуру, подобную данной, пользоваться свойствами подобия для обоснования свойств фигур;

·           применять свойства движений для проведения простейших обоснований свойств фигур.

В повседневной жизни и при изучении других предметов:

·           применять свойства движений и применять подобие для построений и вычислений.

История математики

·           Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;

·           понимать роль математики в развитии России.

Методы математики

·           Используя изученные методы, проводить доказательство, выполнять опровержение;

·           выбирать изученные методы и их комбинации для решения математических задач;

·           использовать математические знания для описания закономерностей в окружающей действительности и произведениях искусства;

·           применять простейшие программные средства и электронно-коммуникационные системы при решении математических задач.

Программа обеспечивает достижения следующих результатов освоения образовательной программы основного общего образования:

Личностные результаты освоения основной образовательной программы:

·         воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;

·         ответственное отношение к учению, готовность и спо­собность обучающихся к саморазвитию и самообразова­нию на основе мотивации к обучению и познанию;

·         осознанный выбор и построение дальнейшей индивиду­альной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а так­же на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;

·         сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики, учитывающего социальное, культурное, языковое, духовное многообразие современного мира.

·         осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению, мировоззрению, культуре, языку, вере, гражданской позиции;

·         умение контролировать процесс и результат учебной и математической деятельности;

·         критичность мышления, инициатива, находчивость, активность при решении математических задач.

Метапредметные результаты освоения основной образовательной программы:

Регулятивные УУД:

·         самостоятельно определять цели обучения, ставить и формулировать новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности;

·         самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

·         соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;

·         оценивать правильность выполнения учебной задачи, собственные возможности ее решения;

·         владеть основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности;

·         составлять (индивидуально или в группе) план решения проблемы;

·         умение осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы.

Познавательные УУД:

• определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное, по аналогии) и делать выводы;
• создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач;
• находить в тексте требуемую информацию (в соответствии с целями своей деятельности); уметь определять возможные источники необходимых сведений, производить поиск информации, анализировать и оценивать её достоверность;
•  осуществлять сравнение и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций;
• создавать математические модели;
• составлять тезисы, различные виды планов (простых, сложных и т.п.);п
• преобразовывать информацию из одного вида в другой ;
• понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания;
• самому создавать источники информации разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности;

·         использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей; умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;

·         выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

·         применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.

Коммуникативные УУД:

• организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; формулировать, аргументировать и отстаивать свое мнение;
• отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами;
• в дискуссии уметь выдвинуть контраргументы;
•  учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения и корректировать его;
• понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;
• уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций;

• умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.

Предметные результаты освоения основной образовательной программы:

• овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (геометрическая фигура, величина) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
• умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
• овладение навыками устных письменных, инструментальных вычислений;
• овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
• усвоение систематических знаний о плоских фигурах и их свойствах, умение применять систематические знания о них для решения геометрических и практических задач;
• умение измерять длины отрезков, величины углов;
• умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочные материалы и технические средства.

Выпускник научится в 9 классе (для использования в повседневной жизни и обеспечения возможности успешного продолжения образования на базовом уровне)

Геометрические фигуры

·           Оперировать на базовом уровне понятиями геометрических фигур;

·           извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде;

·           применять для решения задач геометрические факты, если условия их применения заданы в явной форме;

·           решать задачи на нахождение геометрических величин по образцам или алгоритмам.

В повседневной жизни и при изучении других предметов:

·           использовать свойства геометрических фигур для решения типовых задач, возникающих в ситуациях повседневной жизни, задач практического содержания.

Отношения

В повседневной жизни и при изучении других предметов:

·           использовать отношения для решения простейших задач, возникающих в реальной жизни.

Измерения и вычисления

·           применять теорему Пифагора, базовые тригонометрические соотношения для вычисления длин, величин углов при решении треугольников.

В повседневной жизни и при изучении других предметов:

·           вычислять расстояния на местности в стандартных ситуациях, площади в простейших случаях, применять формулы в простейших ситуациях в повседневной жизни.

Геометрические построения

·           Изображать типовые плоские фигуры и фигуры в пространстве от руки и с помощью инструментов.

В повседневной жизни и при изучении других предметов:

·           выполнять простейшие построения на местности, необходимые в реальной жизни.

Геометрические преобразования

·           Строить фигуру, симметричную данной фигуре относительно оси и точки.

В повседневной жизни и при изучении других предметов:

·           распознавать движение объектов в окружающем мире;

·           распознавать симметричные фигуры в окружающем мире.

Векторы и координаты на плоскости

·           Оперировать на базовом уровне понятиями вектор, сумма векторов, произведение вектора на число, координаты на плоскости;

·           определять приближённо координаты точки по её изображению на координатной плоскости.

В повседневной жизни и при изучении других предметов:

·           использовать векторы для решения простейших задач на определение скорости относительного движения.

История математики

·           Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;

·           знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;

·           понимать роль математики в развитии России.

Методы математики

·           Выбирать подходящий изученный метод для решения изученных типов математических задач;

·           Приводить примеры математических закономерностей в окружающей действительности и произведениях искусства.

Выпускник получит возможность научиться в 9 классе для обеспечения возможности успешного продолжения образования на базовом и углублённом уровнях

Геометрические фигуры

·           Оперировать понятиями геометрических фигур;

·           извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;

·           применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения;

·           формулировать в простейших случаях свойства и признаки фигур;

·           доказывать геометрические утверждения;

·           владеть стандартной классификацией плоских фигур (треугольников и четырёхугольников).

В повседневной жизни и при изучении других предметов:

·           использовать свойства геометрических фигур для решения задач практического характера и задач из смежных дисциплин.

В повседневной жизни и при изучении других предметов:

·           использовать отношения для решения задач, возникающих в реальной жизни.

Измерения и вычисления

·           Оперировать представлениями о длине, площади, объёме как величинами. Применять теорему Пифагора, формулы площади, объёма при решении многошаговых задач, в которых не все данные представлены явно, а требуют вычислений, оперировать более широким количеством формул длины, площади, объёма, вычислять характеристики комбинаций фигур (окружностей и многоугольников) вычислять расстояния между фигурами, применять тригонометрические формулы для вычислений в более сложных случаях, проводить вычисления на основе равновеликости и равносоставленности;

·           проводить простые вычисления на объёмных телах;

·           формулировать задачи на вычисление длин, площадей и объёмов и решать их.

В повседневной жизни и при изучении других предметов:

·           проводить вычисления на местности;

·           применять формулы при вычислениях в смежных учебных предметах, в окружающей действительности.

Геометрические построения

·           Изображать геометрические фигуры по текстовому и символьному описанию;

·           свободно оперировать чертёжными инструментами в несложных случаях,

·           выполнять построения треугольников, применять отдельные методы построений циркулем и линейкой и проводить простейшие исследования числа решений;

·           изображать типовые плоские фигуры и объемные тела с помощью простейших компьютерных инструментов.

В повседневной жизни и при изучении других предметов:

·           выполнять простейшие построения на местности, необходимые в реальной жизни;

·           оценивать размеры реальных объектов окружающего мира.

Преобразования

·           Оперировать понятием движения и преобразования подобия, владеть приёмами построения фигур с использованием движений и преобразований подобия, применять полученные знания и опыт построений в смежных предметах и в реальных ситуациях окружающего мира;

·           строить фигуру, подобную данной, пользоваться свойствами подобия для обоснования свойств фигур;

·           применять свойства движений для проведения простейших обоснований свойств фигур.

В повседневной жизни и при изучении других предметов:

·           применять свойства движений и применять подобие для построений и вычислений.

Векторы и координаты на плоскости

·           Оперировать понятиями вектор, сумма, разность векторов, произведение вектора на число, угол между векторами, скалярное произведение векторов, координаты на плоскости, координаты вектора;

·           выполнять действия над векторами (сложение, вычитание, умножение на число), вычислять скалярное произведение, определять в простейших случаях угол между векторами, выполнять разложение вектора на составляющие, применять полученные знания в физике, пользоваться формулой вычисления расстояния между точками по известным координатам, использовать уравнения фигур для решения задач;

·           применять векторы и координаты для решения геометрических задач на вычисление длин, углов.

В повседневной жизни и при изучении других предметов:

·           использовать понятия векторов и координат для решения задач по физике, географии и другим учебным предметам.

История математики

·           Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;

·           понимать роль математики в развитии России.

Методы математики

·           Используя изученные методы, проводить доказательство, выполнять опровержение;

·           выбирать изученные методы и их комбинации для решения математических задач;

·           использовать математические знания для описания закономерностей в окружающей действительности и произведениях искусства;

·           применять простейшие программные средства и электронно-коммуникационные системы при решении математических задач.

Программа обеспечивает достижения следующих результатов освоения образовательной программы основного общего образования:

Личностные результаты освоения основной образовательной программы:

·         воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;

·         ответственное отношение к учению, готовность и спо­собность обучающихся к саморазвитию и самообразова­нию на основе мотивации к обучению и познанию;

·         осознанный выбор и построение дальнейшей индивиду­альной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а так­же на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;

·         сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики, учитывающего социальное, культурное, языковое, духовное многообразие современного мира.

·         осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению, мировоззрению, культуре, языку, вере, гражданской позиции;

·         умение контролировать процесс и результат учебной и математической деятельности;

·         критичность мышления, инициатива, находчивость, активность при решении математических задач.

Метапредметные результаты освоения основной образовательной программы:

Регулятивные УУД:

·         самостоятельно определять цели обучения, ставить и формулировать новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности;

·         самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

·         соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;

·         оценивать правильность выполнения учебной задачи, собственные возможности ее решения;

·         владеть основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности;

·         составлять (индивидуально или в группе) план решения проблемы;

·         умение осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы.

Познавательные УУД:

• определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное, по аналогии) и делать выводы;
• создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач;
• находить в тексте требуемую информацию (в соответствии с целями своей деятельности); уметь определять возможные источники необходимых сведений, производить поиск информации, анализировать и оценивать её достоверность;
•  осуществлять сравнение и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций;
• создавать математические модели;
• составлять тезисы, различные виды планов (простых, сложных и т.п.);п
• преобразовывать информацию из одного вида в другой ;
• понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания;
• самому создавать источники информации разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности;

·         использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей; умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;

·         выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

·         применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.

Коммуникативные УУД:

• организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; формулировать, аргументировать и отстаивать свое мнение;
• отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами;
• в дискуссии уметь выдвинуть контраргументы;
•  учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения и корректировать его;
• понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;
• уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций;

• умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.

Предметные результаты освоения основной образовательной программы:

• овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (геометрическая фигура, величина) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
• умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
• овладение навыками устных письменных, инструментальных вычислений;
• овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
• усвоение систематических знаний о плоских фигурах и их свойствах, умение применять систематические знания о них для решения геометрических и практических задач;
• умение измерять длины отрезков, величины углов;
• умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочные материалы и технические средства.

3           Содержание учебного предмета, курса

7 класс

Геометрические фигуры

Фигуры в геометрии и в окружающем мире

Геометрическая фигура. Формирование представлений о метапредметном понятии «фигура». 

Точка, линия, отрезок, прямая, луч, ломаная, плоскость, угол, биссектриса угла и её свойства, виды углов, многоугольники, круг.

Многоугольники

Треугольники. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренный треугольник, его свойства и признаки. Равносторонний треугольник. Прямоугольный, остроугольный, тупоугольный треугольники. Внешние углы треугольника. Неравенство треугольника.

Окружность, круг

Окружность, круг, их элементы и свойства.

Отношения

Равенство фигур

Свойства равных треугольников. Признаки равенства треугольников.

Параллельно­сть прямых

Признаки и свойства параллельных прямых. Аксиома параллельности Евклида. Перпендикулярные прямые

Прямой угол. Перпендикуляр к прямой. Наклонная, проекция.

Измерения и вычисления

Величины

Понятие величины. Длина. Измерение длины. Единицы измерения длины. Величина угла. Градусная мера угла.

Измерения и вычисления

Инструменты для измерений и построений; измерение и вычисление углов, длин (расстояний), площадей.

Расстояния

Расстояние от точки до прямой.

Геометрические построения

Геометрические построения для иллюстрации свойств геометрических фигур.

Инструменты для построений: циркуль, линейка, угольник. Простейшие построения циркулем и линейкой: построение биссектрисы угла, перпендикуляра к прямой, угла, равного данному,

Построение треугольников по трём сторонам, двум сторонам и углу между ними, стороне и двум прилежащим к ней углам.

             История математики

От земледелия к геометрии.

Геометрия и искусство. Геометрические закономерности окружающего мира.«Начала» Евклида. Л Эйлер, Н.И.Лобачевский. История пятого постулата.

8 класс

Геометрические фигуры

Фигуры в геометрии и в окружающем мире

Осевая симметрия геометрических фигур. Центральная симметрия геометрических фигур.

Многоугольники

Многоугольник, его элементы и его свойства. Распознавание некоторых многоугольников. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

Четырёхугольники. Параллелограмм, ромб, прямоугольник, квадрат, трапеция, равнобедренная трапеция. Свойства и признаки параллелограмма, ромба, прямоугольника, квадрата.

Окружность, круг

Центральные и вписанные углы. Касательная и секущая к окружности, их свойства. Вписанные и описанные окружности для треугольников.

Отношения

Равенство фигур

Свойства равных треугольников. Признаки равенства треугольников.

Параллельно­сть прямых

Теорема Фалеса.

Перпендикулярные прямые

Серединный перпендикуляр к отрезку. Свойства и признаки перпендикулярности.

Подобие

Пропорциональные отрезки, подобие фигур. Подобные треугольники. Признаки подобия.

Взаимное расположение прямой и окружности, двух окружностей.

Измерения и вычисления

Величины

Понятие о площади плоской фигуры и её свойствах. Измерение площадей. Единицы измерения площади.

Измерения и вычисления

Тригонометрические функции острого угла в прямоугольном треугольнике. Формулы площади треугольника, параллелограмма и его частных видов. Сравнение и вычисление площадей. Теорема Пифагора.

Геометрические построения

Деление отрезка в данном отношении.

Геометрические преобразования

Преобразования

Понятие преобразования. Представление о метапредметном понятии «преобразование». Подобие.

             История математики

Школа Пифагора

Пифагор и его школа. Фалес, Архимед. Платон и Аристотель. Построение правильных многоугольников. История числа π. Золотое сечений

9 класс

Геометрические фигуры

Геометрические фигуры в пространстве (объёмные тела)

Многогранник и его элементы. Названия многогранников с разным положением и количеством граней. Первичные представления о пирамиде, параллелепипеде, призме, сфере, шаре, цилиндре, конусе, их элементах и простейших свойствах.

Окружность, круг

Вписанные и описанные окружности четырёхугольников, правильных многоугольников.

Измерения и вычисления

Величины

Представление об объёме и его свойствах. Измерение объёма. Единицы измерения объёмов.

Измерения и вычисления

Тригонометрические функции тупого угла. Вычисление элементов треугольников с использованием тригонометрических соотношений. Формулы длины ок­ружности и площади круга. Вычисление площадей. Теорема синусов. Теорема косинусов.

Расстояния

Расстояние между точками. Расстояние между фигурами.

Геометрические преобразования

Движения

Осевая и центральная симметрия, поворот и параллельный перенос. Комбинации движений на плоскости и их свойства.

Векторы и координаты на плоскости

Векторы

Понятие вектора, действия над векторами, использование векторов в физике, разложение вектора на составляющие, скалярное произведение.

Координаты

Основные понятия, координаты вектора, расстояние между точками. Координаты середины отрезка. Уравнения фигур.

Применение векторов и координат для решения простейших геометрических задач.

История математики

Появление метода координат, позволяющего переводить геометрические объекты на язык алгебры.

Построение правильных многоугольников. Триссекция угла. Квадратура круга. Удвоение куба.

4   Тематическое планирование с определением видов учебной деятельности

обучающихся

7 класс:

8 класс

9 класс

4           Оценочные материалы.

Виды контроля: текущий (на каждом уроке), периодический (по мере прохождения темы, раздела программы), итоговый (в конце четверти, полугодия, накануне перевода в следующий класс)

По формам организации контроль  индивидуальный, групповой, фронтальный и комбинированный. Учащийся вызывается к доске, или опрашивается весь класс. Вопросно- ответная форма диагностики активизирует работу всего класса. Фронтальные и индивидуальные формы работы проводятся в виде тестирования по индивидуальным тестам, тестирования  по одному варианту, контрольной работы по вариантам (Содержание заданий разделено условно на две части. Первая соответствует начальному и среднему уровню достижений и дается, как правило, в тестовой форме (с выбором варианта ответа) Задания этой части находятся обозначены «часть А». Вторая часть соответствует достаточному (часть В) и высокому (часть С) уровням, задача, отмеченная звездочкой, предназначена для более подготовленного ученика)  письменный опрос (диктант), зачёт-беседа по материалам курса после каждой главы учебника, устного опроса, опроса с помощью ПК (тест с выбором ответа), рефератов (исследовательская работа), творческого задания (изготовление пособий, карточек), смотра  знаний, конкурсов, игр, олимпиад, викторин.

Опираясь на следующие рекомендации, учитель оценивает знания и умения учащихся с учетом их индивидуальных особенностей.

1.    Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.

2.    Основными формами проверки знаний и умений учащихся по математике являются письменная контрольная работа и устный опрос.

     При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения. Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.

3.     Среди погрешностей выделяются ошибки и недочёты. Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.

     К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в программе основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа.

     Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах — как недочет.

4.    Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.

     Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты я обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.

     Решение задачи считается безупречным, если правильно выбран способ решения, само­ решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.

    Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т. е. за ответ выставляется одна из отметок: 1 (плохо), 2 (неудовлетворительно), 3 (удовлетворительно), 4 (хорошо), 5 (отлично).

5.    Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им заданий.

Критерии ошибок

             К грубым ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;

             К негрубым ошибкам относятся: потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им;

             К недочетам относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях

Оценка устных ответов учащихся

Ответ оценивается отметкой «5», если ученик:

ü  полно раскрыл содержание материала в объеме, предусмотренном программой и учебником,

ü  изложил материал грамотным языком в определенной логической последовательности, точно

используя математическую терминологию и символику;

ü  правильно выполнил рисунки, чертежи, сопутствующие ответу;

ü  показал   умение   иллюстрировать   теоретические   положения   конкретными   примерами,

применять их в новой ситуации при выполнении практического задания;

ü  продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность

и устойчивость используемых при отработке умений и навыков;

ü  отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности

при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по

замечанию учителя.

Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

ü  в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

ü  допущены один - два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;

ü  допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.

Отметка «3»ставится в следующих случаях:

ü  неполно или непоследовательно раскрыто содержание материала, по показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»);

ü  имелись затруднения или допущены ошибки  в определении  понятий, использовании

математической терминологии, чертежах, выкладках, исправленные после нескольких

наводящих вопросов учителя;

ü  ученик не справился с применением теории в новой ситуации при выполнении практического

задания, но выполнил задания обязательного уровня сложности по данной теме;

ü  при знании теоретического материала выявлена недостаточная сформированность основных

умений и навыков.

Отметка «2»ставится в следующих случаях:

ü  не раскрыто основное содержание учебного материала;

ü  обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

ü  допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Оценка письменных работ учащихся

Отметка «5»ставится, если:

ü  работа выполнена полностью;

ü  в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).

Отметка «4»ставится, если:

ü  работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

ü  допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

Отметка «3» ставится, если:

ü  допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2»ставится, если:

ü  допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере.

1)      Контрольно-измерительные материалы (7 класс)

Контрольная работа №1  по теме: «Начальные геометрические сведения»

Цель:проверить

·          знания видов углов (вертикальные, смежные), свойство биссектрисы угла;

·          навыки решения геометрических задач по теме.

В-I

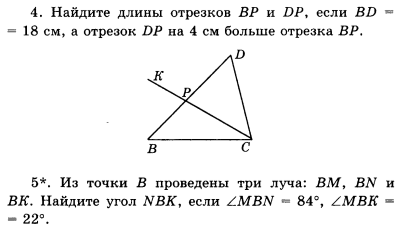
В-II

К.р. №2 по теме: «Признаки равенства треугольников»

В-I

Часть А.

Цель:проверить

·          знания по определению медианы, биссектрисы и высоты в треугольнике;

·          навыки решения геометрических задач по теме.

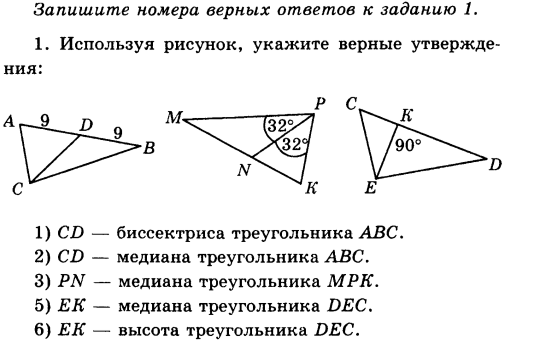
Часть В. 

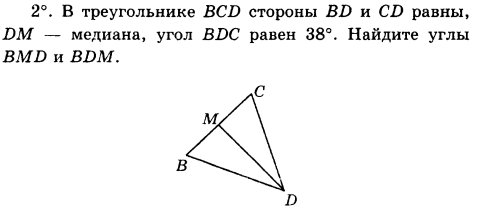
Часть С.   Запишите обоснованное решение.

В- II

Часть А.  Запишите номера верных ответов.

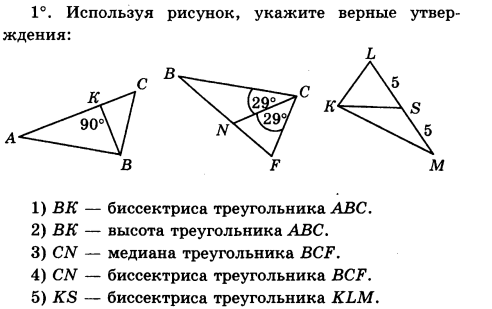
Часть В.

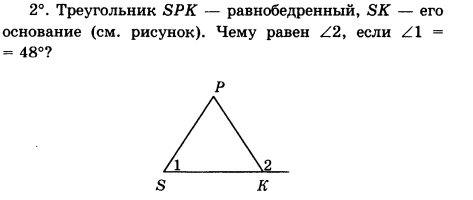
Часть С.   Запишите обоснованное решение.

К.р. №3  по теме: «Признаки параллельности прямых»

Цель:проверить

·          знания видов углов (накрест лежащие, односторонние, соответственные);

·          навыки решения геометрических задач по теме.

В-I

Часть А.Запишите номера верных ответов.

Часть В. Запишите ответ к заданию.

Часть С.   Запишите обоснованное решение.

В- II

Часть А.  Запишите номера верных ответов.

Часть В. Запишите ответ к заданию.

Часть С.   Запишите обоснованное решение.

К.р. №4  по теме: «Соотношение между сторонами  и углами треугольника»

Цель: проверить

·          навык определения внешних и внутренних углов треугольника, их свойств;

·          навыки решения геометрических задач по теме.

В-I

Часть А.Запишите номера верных ответов.

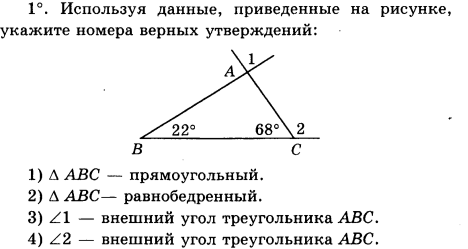
Часть В. Запишите ответ к заданию.

Часть С.   Запишите обоснованное решение.

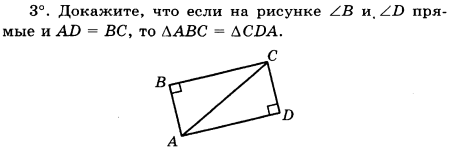
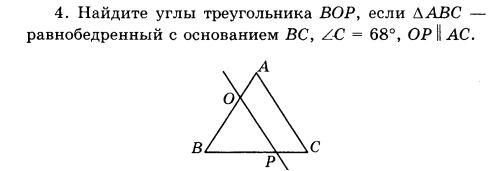
В- II

Часть А.  Запишите номера верных ответов.

Часть В. Запишите ответ к заданию.

Часть С.   Запишите обоснованное решение.

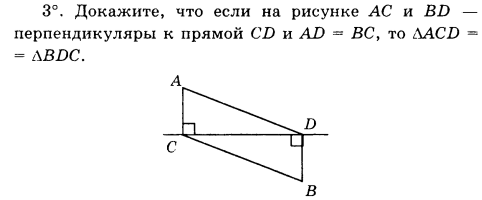
К.р. №5 по теме: «Прямоугольный треугольник. Построение треугольника по трем элементам»

Цель:проверить

·          свойства прямоугольного треугольника; навык построения треугольника по трем элементам;

·          навыки решения геометрических задач по теме.

В-I

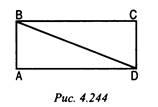
В-II

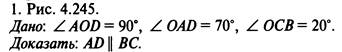
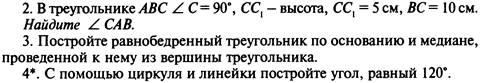
Контрольная работа №6 (итоговая)

Цель:  проанализировать результаты усвоения основных тем программы за учебный год.

В- I   

Часть А.  Запишите номера верных ответов.

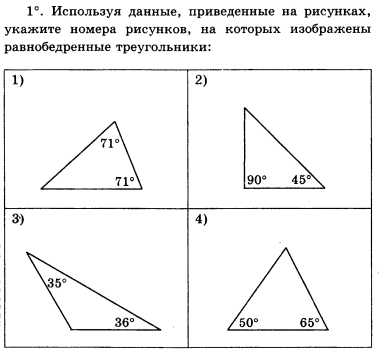
Часть В. Запишите ответ к заданию.

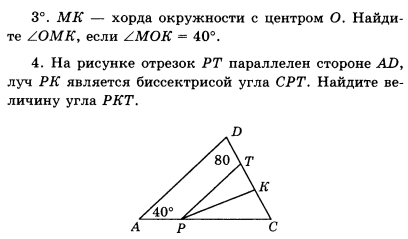
Часть С.   Запишите обоснованное решение.

В- II

Часть А.Запишите номера верных ответов.

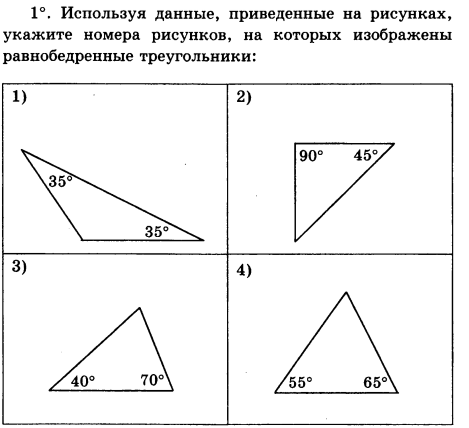
Часть В. Запишите ответ к заданию.

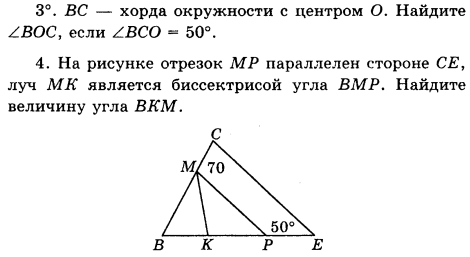
Часть С.   Запишите обоснованное решение.

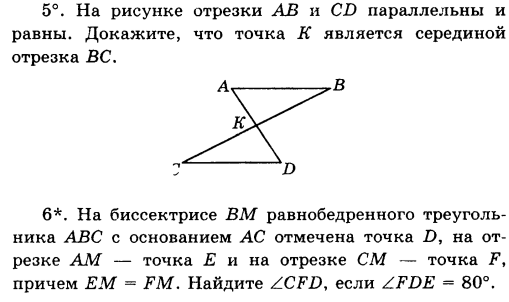
2)      Контрольно-измерительные материалы (8 класс)

Контрольная работа №1 по теме: «Четырехугольники»

Цель:проверить уровень знаний по темам:

В-I

Часть А.

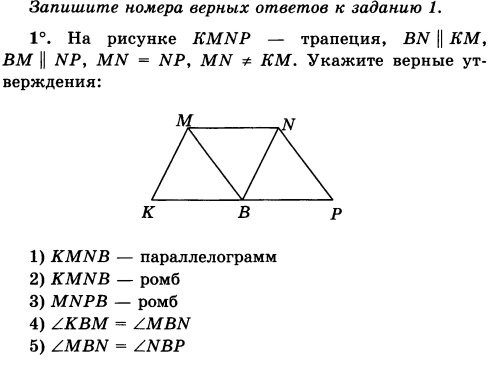
Часть В.

Запишите решение к следующим заданиям.

Часть С.

Запишите обоснованное решение к задачам 4 и 5.

5˚

B-IIЧасть А.

Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 4 и 5.

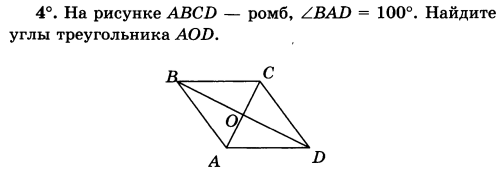
5˚

Контрольная работа №2 по теме: «Теорема Пифагора. Площади»

Цель:проверить уровень знаний о темам:

В-I

Часть А.

Часть В.

Запишите решение к следующим заданиям.

Часть С.

Запишите обоснованное решение к задачам 3 - 5.

B-II

Часть А.

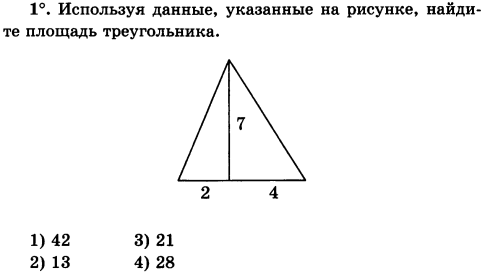
Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 3 - 5.

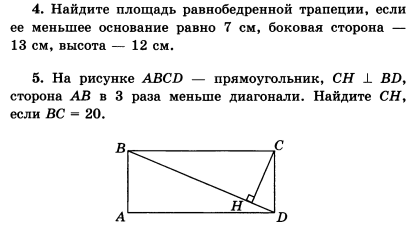
Контрольная работа №3 по теме: «Подобные треугольники»

Цель:проверить уровень знаний по темам:

• отношение площадей подобных треугольников.

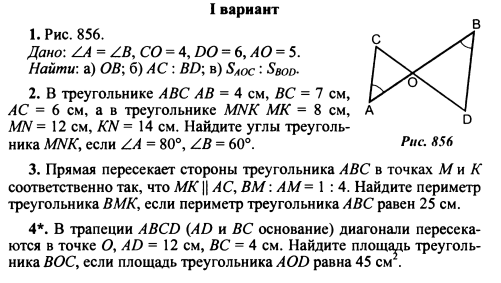
Контрольная работа №4 по теме: «Подобие фигур. Соотношение между сторонами и углами в треугольнике»

Цель:проверить уровень знаний по темам:

В-I

Часть А.

Запишите номера верных ответов, записав краткое решение:

Часть В.

Запишите решение к следующим заданиям.

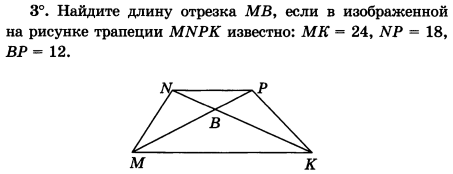
Часть С.

Запишите обоснованное решение к задачам 5 - 6.

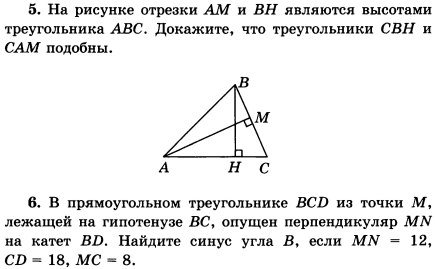
B-II

Часть А.

Запишите номера верных ответов, записав краткое решение:

Часть В.

Запишите решение к следующим заданиям

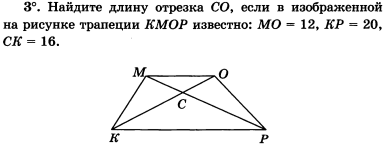
Часть С.

Запишите обоснованное решение к задачам 5-6.

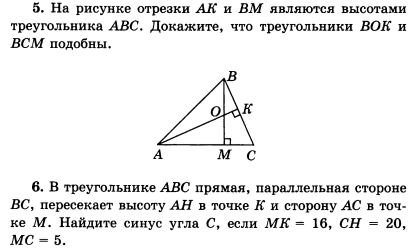
Контрольная работа №5  по теме: «Окружность»

Цель:проверить уровень знаний по темам:

В-I

Часть А

Часть В.

Запишите решение к следующим заданиям.

Часть С.

Запишите обоснованное решение к задачам 5 и 6.

B-II

Часть А.

Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 5 и 6.

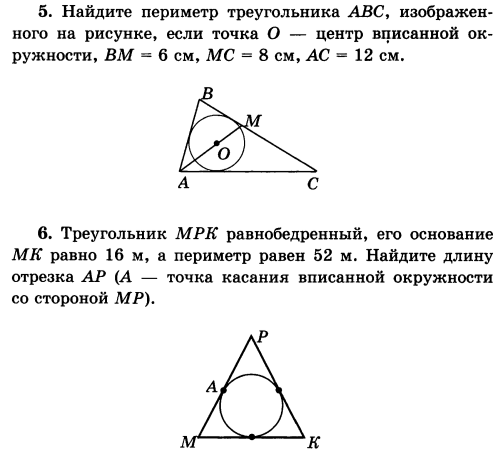
Итоговая контрольная работа №6 за 8 класс.

Цель:

B-I

Часть А.

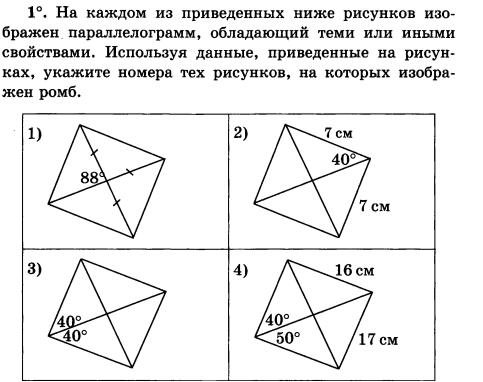
Часть В.

Запишите решение к следующим заданиям

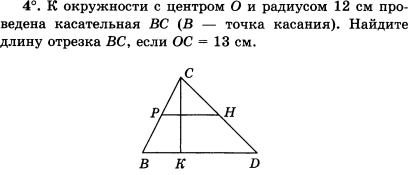
Часть С.

Запишите обоснованное решение к задачам 6 и 7.

B-II

Часть А.

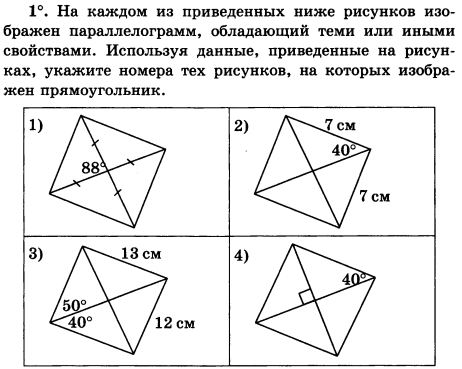
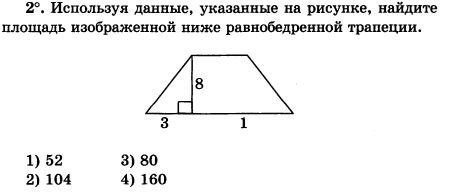
Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 6 и 7.

3)      Контрольно-измерительные материалы (9 класс)

Контрольная работа №1  по теме: «Векторы. Метод координат»

Цель:проверитьзнания по темам:

·         

B-I

Часть А.

Запиши верные варианты ответов

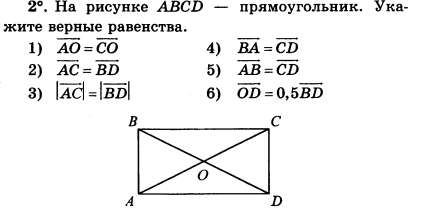
Часть В.

Запишите решение к следующим заданиям

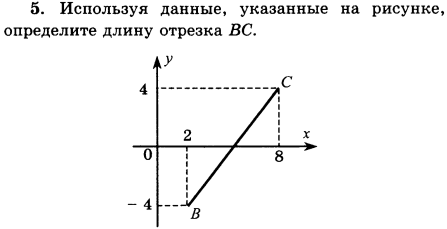
Часть С.

Запишите обоснованное решение к задачам  6 и 7.

B-II

Часть А.

Запиши верные варианты ответов

Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 6 и 7

Контрольная работа №2  по теме: «Соотношение между сторонами и углами треугольника. Скалярное произведение векторов»

Цель:проверить знания по темам:

B-I

Часть А.

Запиши верные варианты ответов

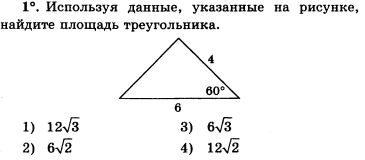
Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 5, 6 и 7.

B-II

Часть А.

Запиши верные варианты ответов

Часть В.

Запишите решение к следующим заданиям

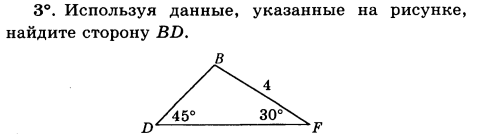
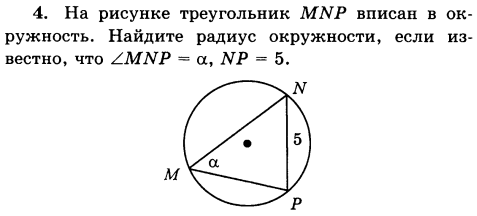
Часть С.

Запишите обоснованное решение к задачам 5, 6 и 7.

Контрольная работа №3  по теме: «Длина окружности и площадь круга»

Цель:проверить знания по темам:

B-I

Часть А.

Запиши верные варианты ответов

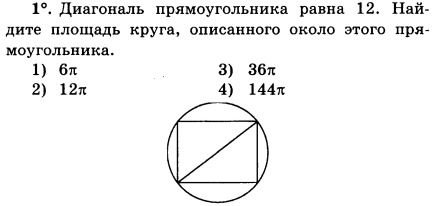
Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 5 и 6.

B-II

Часть А.

Запиши верные варианты ответов

Часть В.

Запишите решение к следующим заданиям

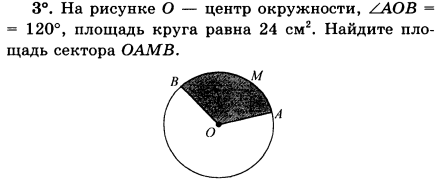
Часть С.

Запишите обоснованное решение к задачам 5 и 6.

Контрольная работа №4  по теме: «Движение»

Цель:проверить знания по темам:

B-I

Часть А.

Запиши верные варианты ответов

Часть В.

Запишите решение к следующим заданиям

Часть С.

Выполните построения к задачам 3, 4 и 5.

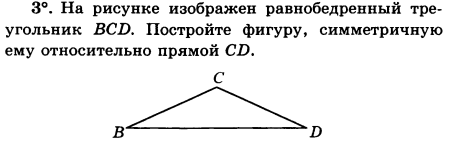
B-II

Часть А.

Запиши верные варианты ответов

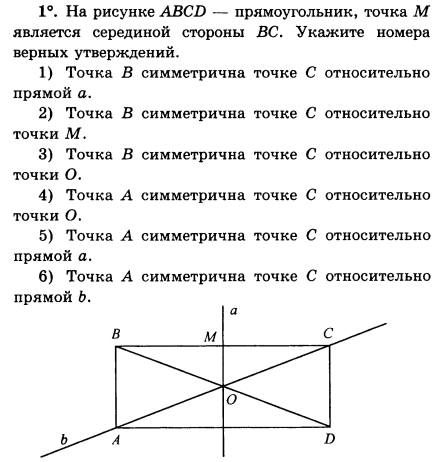
Часть В.

Запишите решение к следующим заданиям

Часть С.

Выполните построения, указанные в задачах 3, 4 и 5.

Контрольная работа №5  по теме: «Начальные сведения из стереометрии»

Цель:проверить знания  по темам:

B-I

Часть А.

Запиши верные варианты ответов

Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 4 и 5.

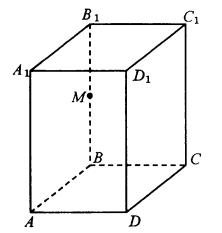
B-II

Часть А.

Запиши верные варианты ответов

Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 4 и 5.

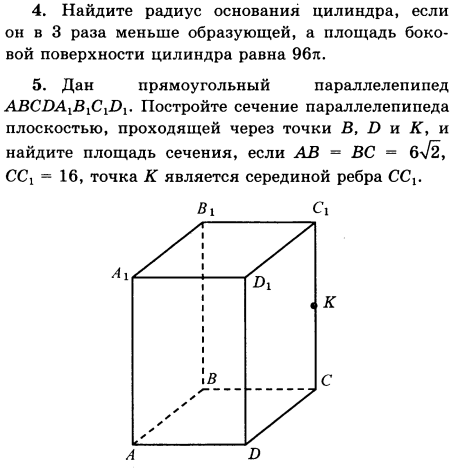
Итоговая контрольная работа №6.

Цель:проверить знания по темам:

B-I

Часть А.

Запиши верные варианты ответов

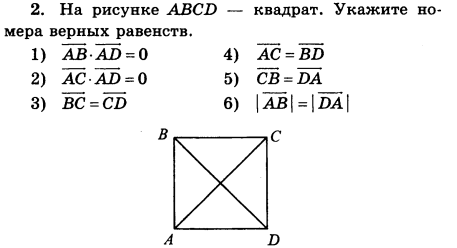
Часть В.

Запишите решение к следующим заданиям

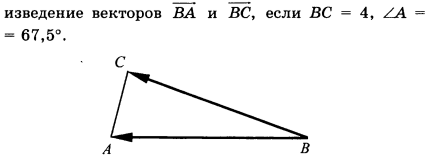
Часть С.

Запишите обоснованное решение к задачам 5, 6 и 7.

B-II

Часть А.

Запиши верные варианты ответов

Часть В.

Запишите решение к следующим заданиям

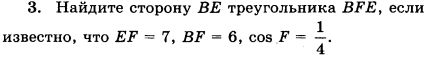
Часть С.

Запишите обоснованное решение к задачам 5, 6 и 7.

Итоговая контрольная работа за курс основной школы №7.

Цель:проверить знания по темам:

B-I

Часть А.

Запиши верные варианты ответов

Часть В.

Запишите решение к следующим заданиям

Часть С.

Запишите обоснованное решение к задачам 6 и 7.

B-II                                                                                                                                         

Часть А.

Запиши верные варианты ответов

Часть В.

Запишите решение к следующим заданиям

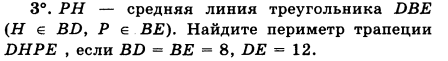
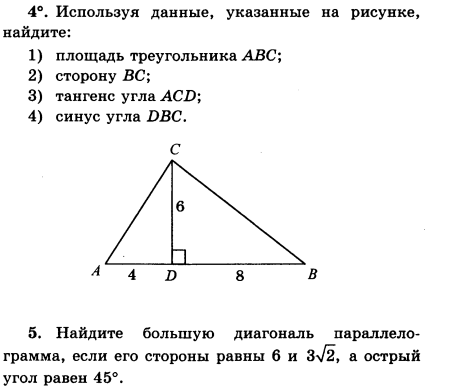
Часть С.

Запишите обоснованное решение к задачам 6 и 7.

Скачано с www.znanio.ru