Добавить материал

и получить 10 документов
и свидетельство СМИ

Витальевна Ливанда Витальевна

рабочая программа по геометрии 8 класс

Образовательные программы
doc
19.01.2017

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

рабочая программа для учащихся 8 класса по геометрии рас читана на 2 часа в неделю по учебнику Атаносян. В программе предусмотрены темы на повторение, контрольные работа. Программа направлена на достижение следующих целей: овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;

8кл геометрия 2014-15г..doc

*№ УРОКА*	*Дата фактич*	*ДАТА*	*ТЕМА УРОКА*	*ТИП УРОКА*	*ЭЛЕМЕНТЫ СОДЕРЖАНИЯ УРОКА*	*ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ*	*МОНИТО-* *РИНГ*	*ЭЛЕМЕН* *ТЫ ДОПОЛНИ-* *ТЕЛЬНОГО СОДЕРЖАНИЯ*	*ДОМАШ-* *НЕЕ* *ЗАДАНИЕ*
1			Многоугольники. Выпуклый многоугольник	УОНМ	Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника	Знать: определение многоугольника, формулу суммы углов выпуклого многоугольника. Уметь: распознавать на чертежах многоугольники и выпуклые многоугольники, используя определение	УО		п. 39 363, 366
2			Четырехуголь-ник	УПЗУ	Многоугольники. Элементы многоугольника	Знать: формулу суммы углов многоугольника. Уметь: применять формулу суммы углов выпуклого многоугольника при нахождении элементов многоугольника	Индивидуальные карточки		№ 365, 368, 369
3			Параллелог-рамм	УОНМ	Параллелограмм, его свойства	Знать: определение параллелограмма и его свойства. Уметь: распознавать на чертежах среди четырехугольников	СР№1 ДМ (15 мин)	Дополнительные свойства параллелограм-ма	п. 42 № 372 в, 376 б, г
4			Признаки параллелограмма	КУ	Признаки параллелограмма	Знать: формулировки свойств и признаков параллелограмма. Уметь: доказывать,	ФО		п. 43 №380,382
5			Решение задач, на применение свойств	УПЗУ		Уметь выполнять чертежи по условию задачи, находить углы и стороны параллелограмма, используя свойства углов и сторон	опрос		№ 420, 425
6			Трапеция	КУ	трапеция. средняя линия трапеции. Равнобедренная трапеция, ее свойства	Знать определение трапеции, свойства равнобедренной трапеции. Уметь распознавать трапецию, ее элементы, виды на чертежах, находить углы и стороны равнобедренной трапеции, используя ее свойства	УО		П.44, № 384, 387
7			Свойства и признаки равнобедренной трапеции	УОН	Теорема Фалеса	Знать формулировку теоремы Фалеса и основные этапы ее доказательства. Уметь применять теорему при решении задач	Решение по готовым чертежам. с/р		№ 391, 392; РТ№17
8			Задачи на построение	КУ	Задачи на построение	Знать основные задачи на построение. Уметь: делить отрезок на и равных частей, выполнять необходимые построения	Ср ДМ (15 мин)	Деление отрезка на n- равных частей	397,393 б, 395, 393 а
9			Прямоугольник	УОНМ	Прямоугольник, его элементы, свойства	Знать определение прямоугольника, его элементы, свойства и признаки. Уметь: распознавать на чертежах, находить стороны, используя свойства углов и диагоналей	УО		П.45, № 399, 400, 404
10			Ромб, квадрат	КУ	понятие ромба, квадрата, свойства и признаки.	Знать определение ромба, квадрата как частных видов параллелограмма. Уметь: распознавать и изображать ромб, квадрат, находить стороны и углы, используя свойства фигур	с/р Проверка дз		П.46, 405,403, 411
11				КУ	Прямоугольник, ромб, квадрат	Знать определения, свойства и признаки прямоугольника, ромба, квадрата. Уметь выполнять чертеж по условию задачи, применяя свойства и признаки при решении задач.	ФО		П.47, 415,б, 413 а,
12			Решение задач Осевая и центральная симметрия	УПЗУ	Осевая и центральная симметрия как свойство геометрических фигур	Знать виды симметрии в многоугольниках. Уметь стоить симметричные точки и распознавать фигуры, фигуры, обладающие осевой и центральной симметрией			426,428
13			Решение задач, зачет по теме	УОСЗ	Четырехугольники: элементы, свойства и признаки.	Знать определения, свойства и признаки четырехугольников. Уметь: находить стороны квадрата, если известны части сторон используя свойства прямоугольного треугольника.	Зачет по теории		413
14			Контрольная работа № 1 по теме: «Четырехугольники»	УКЗУ	Свойства и признаки прямоугольника, трапеции, ромба, параллелограмма	Уметь: находить в прямоугольнике угол между диагоналями, используя свойство диагоналей, углы в прямоугольной или равнобедренной трапеции, используя свойства трапеции, стороны параллелограмма	КР№1 ДМ (40 мин)		РТ № 20, 22
15			Анализ контрольной работы. Площадь многоугольника	УОНМ	Понятие о площади. Равносоставленные и равновеликие фигуры. Свойства площадей	Знать: представление о способе измерения площади многоугольника, свойства площадей. Уметь: вычислять площадь квадрата	ФО		п. 48,49 № 447, 452 б, 453
16			Площадь прямоугольника	КУ	Площадь прямоугольника	Знать: формулу площади прямоугольника. Уметь: находить площадь прямоугольника, используя формулу	Проверка дом. зад. с/р		п. 50 №454,455, 456 РТ № 32
17			Площадь параллелограмма	УОНМ	Площадь параллелограмма	Знать: формулу вычисления площади параллелограмма	УО		п. 51 № 460, 464 а, 459 в, г
18			Площадь параллелограмма	УПЗУ	Площадь параллелограмма	Уметь: выводить формулу площади параллелограмма и находить площадь, используя формулу.	СР№10 ДМ (15 мин)		№ 462,465
19			Площадь треугольника	КУ	Формула площади треугольника	Знать: формулу площади треугольника. Уметь: доказывать теорему о площади треугольника, вычислять площадь треугольника, используя формулу	УО, карточки	Формула Герона	п. 52 № 468 в, 473,469 РТ № 37
20			Площадь треугольника	УПЗУ	Площадь треугольника. Теорема об отношении площадей треугольников, имеющих по равному углу	Знать: формулировку теоремы об отношении площадей треугольников, имеющих по равному углу. Уметь: доказывать теорему и применять ее для решения задач	СР (10 мин)		№ 469 а, 479 а, 472
21			Площадь трапеции, ромба и других четырехугольников	КУ	Теорема о площади трапеции	Знать: формулировку теоремы о площади трапеции и этапы ее доказательства. Уметь: находить площадь трапеции, используя формулу	диктант		п. 53 476 б, 480 а, 481
22			Площадь трапеции, ромба и других четырехугольников	КУ	Формула площади трапеции				№478 РТ №44
23			Решение задач по теме «Площадь»	УОСЗ	Формулы площадей: прямоугольника, треугольника, параллелограмма, трапеции	Знать и уметь: применять формулы площадей при решении задач	СР (15 мин)		№477 в
24			Решение задач по теме «Площадь»	УПЗУ	Площадь четырехугольника	Уметь: решать задачи на вычисление площадей. Знать и уметь выводить формулы площадей параллелограмма, трапеции и треугольника.	Проверка задач сам решения		РТ № 35, 40,41
25			Теорема Пифагора	УОНМ	Теорема Пифагора	Знать формулировку теоремы Пифагора, основные этапы ее доказательства. Уметь: находить стороны треугольника, используя теорему Пифагора	ФО		П.54, 483 в,г, 484 г, д, 486 в РТ№47
26			Теорема, обратная теореме Пифагора	УОНМ	Теорема, обратная теореме Пифагора	Знать формулировку теоремы, обратной теореме Пифагора, основные этапы ее доказательства. Уметь: находить стороны треугольника, используя теорему, обратную теореме Пифагора	ФО, с/р		П.55, 498, г,д. 499 б, 488.
27			Решение задач	УПЗУ	Применение теоремы Пифагора и теоремы, обратной теореме Пифагора	Знать формулировки теоремы Пифагора и ей обратной обратной. Уметь: выполнять чертеж по условию задачи, находить элементы треугольника, используя теорему Пифагора	СР 13 ДМ (15 мин)		489 а,в, 491 а, 493 РТ№50
28			Решение задач, зачет по теме площади	УОСЗ	Применение теоремы Пифагора и теоремы, обратной теореме Пифагора	Знать формулировки теоремы Пифагора и ей обратной обратной. Уметь: выполнять чертеж по условию задачи, находить элементы треугольника, используя теорему Пифагора	текущий		490 а, 494 а, 495 б, РТ№50
29			Решение задач	УОСЗ		Определять вид треугольника, используя теорему, обратную теореме Пифагора	карточки		490 в, 497, 503, 518
30			Контрольная работа № 2 по теме: «Площадь»	УКЗУ	Формулы вычисления площадей параллелограмма, трапеции. Теорема Пифагора и ей обратная	Уметь находить площади треугольника по высоте и стороне. Находить элементы прямоугольного треугольника, используя теорему Пифагора. Находить площадь и периметр ромба по его диагоналям	КР№2 ДМ (40 мин)		Подготовить презентацию
31			Анализ контрольной работы. Определение подобных треугольников	УОНМ	Подобие треугольников. Коэффициент подобия	Знать: определение пропорциональных отрезков подобных треугольников, свойство биссектрисы треугольника. Уметь: находить элементы треугольника, используя свойство биссектрисы о делении противоположной стороны	УО		п. 56, 57 № 534 а, б, 536 а, 538
32			Отношение площадей подобных фигур	КУ	Связь между площадями подобных фигур	Знать: формулировку теоремы об отношении площадей подобных треугольников. Уметь: находить отношения площадей, составлять уравнения, исходя из условия задачи	СР№ 16 ДМ (15 мин)		п. 58 № 544, 546, 549
33			Первый признак подобия треугольников	УОНМ	Первый признак подобия треугольников	Знать: формулировку первого признака подобия треугольников, основные этапы его доказательства. Уметь: доказывать и применять при решении задач первый признак подобия треугольников, выполнять чертеж по условию задачи	ФО		459, 550, 516,555
34			Первый признак подобия треугольников	УЗИМ	Первый признак подобия треугольников		УО		552 а, 6, 557 в, 558, 556
35			Второй и третий признаки подобия треугольников	УОНМ	Второй и третий признаки подобия треугольников	Знать: формулировки второго и третьего признаков подобия треугольников. Уметь: проводить доказательства признаков, применять их при решении задач	Инди- . виду-альные карточки		п. 60, 61 № 559, 560, 561
36			Второй и третий признаки подобия треугольников	УПЗУ	Второй и третий признаки подобия треугольников		СР18 ДМ (15 мин)		№ 562, 563, 604
37			Решение задач по теме: «Признаки подобия треугольников»	УОСЗ	Применение признаков подобия при решении задач	Уметь: доказывать подобия треугольников и находить элементы треугольника, используя признаки подобия	Проверка задач сам, р		№ 565, 605
38			Контрольная работа № 3 по теме: «Признаки подобия треугольников»	УКЗУ	Признаки подобия треугольников	Уметь: находить стороны, углы, отношения сторон, отношение периметров и площадей подобных треугольников, используя признаки подобия. Доказывать подобия треугольников, используя наиболее эффективные признаки подобия	КР№3 ДМ (40 мин)		РТ № 55, 58
39			Анализ контрольной работы. Средняя линия треугольника	УОНМ	Средняя линия треугольника	Знать: формулировку теоремы о средней линии треугольника. Уметь: проводить доказательство теоремы о средней линии треугольника, находить среднюю линию треугольника	УО		п. 62 № 556, 570, 571 РТ№61,63
40			Свойство медиан треугольника	КУ	Свойство медиан треугольника	Знать: формулировку свойства медиан треугольника. Уметь находить элементы треугольника, используя свойство медианы	СР №19 дм (15 мин)		№ 568,569 РТ № 64, 65
41			Пропорциональные отрезки	КУ	Среднее пропорциональное	Знать понятие среднего пропорционального, свойство высоты прямоугольного треугольника проведенной из вершины прямого угла. Уметь: находить элементы прямоугольного треугольника, используя свойство высоты	Индии. карточки		п. 63 № 572 а, в, 573,574 б
42			Пропорциональные отрезки в прямоугольном треугольнике	УПЗУ	Пропорциональные отрезки в прямоугольном треугольнике	Знать: теоремы о пропорциональности отрезков в прямоугольном треугольнике. Уметь: использовать теоремы при решении задач	ФО		№ 575, 577, 579
43			Измерительные работы на местности	УПЗУ	Применение подобия треугольников в измерительных работах на местности	Знать, как находить расстояние до недоступной точки. Уметь использовать подобие треугольников в измерительных работах на местности, описывать реальные ситуации на языке геометрии	СР № 20 ДМ (15 мин)		п. 64 в. 13 №580,581
44			Задачи на построение	УОСЗ	Задачи на построение	Знать этапы построения. Уметь строить биссектрису, медиану, высоту треугольника, угол равный данному, прямую, параллельную данной.	УО		№ 585 б, в, 587,590
45			Задачи на построение методом подобных треугольников	УПЗУ	Метод подобия	Знать метод подобия. Уметь: применять метод подобия при решении задач на построение	текущий		п. 42 в. 14 № 606, 607, 629
46			Синус, косинус и тангенс острого угла прямоугольного треугольника	УОНМ	Понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника. Основное тригонометрическое тождество	Знать понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника. Основное тригонометрическое тождество. Уметь: находить значения одной из тригонометрических функций по значению другой	ФО		П.66, 591 в,г, 592 б, г, 593 в РТ№73
47			Значения синуса, косинуса, тангенса для углов 30°, 45°, 60°, 90°		Синус, косинус, тангенс углов 30°, 45°, 60°, 90°	Знать значение синуса, косинуса, тангенса для углов 30°, 45°, 60°, 90° . Уметь: определять значения синуса, косинуса, тангенса по заданному значению углов	УО		П.67, № 595, 597, 598 РТ № 76
48			Соотношения между сторонами и углами прямоугольного треугольника	УОНМ	Решение прямоугольных треугольников	Знать соотношения между углами и сторонами прямоугольного треугольника. Уметь: решать прямоугольные треугольники, используя определение синуса, косинуса, тангенса острого угла	СР 23, ДМ 15 мин		П.63-67, № 599, 601, 602 РТ № 77
49			Решение задач	УОСЗ	Задачи на применение теории подобия треугольников и соотношений между сторонами	Знать и уметь: применять теорию подобия треугольников, соотношения между сторонами и углами прямоугольного треугольника при решении задач. Уметь: выполнять чертеж по условию задачи, решать геометрические задачи с использованием тригонометрии	Проверка задач самостоятельного решения		№ 623, 625, 630
50			Контрольная работа № 4 «Применение подобия треугольников, соотношения между сторонами и углами прямоугольного треугольника»	УПЗУ	Средняя линия треугольника. Свойство медиан треугольника. Соотношения между сторонами и углами прямоугольного треугольника	Уметь: находить стороны треугольника по отношению средних линий и периметру. Решать прямоугольный треугольник, используя соотношения между сторонами и углами. Находить стороны треугольника, используя свойство точки пересечения медиан	КР№4 ДМ (40 мин)		С-24ДМ
51			Анализ контрольной работы. Взаимное расположение прямой и окружности	УОНМ	Взаимное расположение прямой и окружности	Знать: случаи взаимного расположения прямой и окружности. Уметь: определять взаимное расположение прямой и окружности, выполнять чертеж по условию задачи	ФО	Метрические соотношения в окружности	п. 68 №631 в, г, 632,633
52			Касательная к окружности	КУ	Касательная и секущая к окружности. Точка касания	Знать: понятие касательной, точек касания, свойство касательной и ее признак. Уметь: доказывать теорему о свойстве касательной и ей обратную, проводить касательную к окружности	Теоретический опрос		п. 69 № 634,636, 693 РТ№83
53			Решение задач	УПЗУ	Касательная и секущая к окружности. Равенство отрезков касательных, проведенных из одной точки. Свойство касательной и ее признак	Знать: взаимное расположение прямой и окружности; формулировку свойства касательной о ее перпендикулярности радиусу; формулировку свойства отрезков касательных, проведенных из одной точки. Уметь: находить радиус окружности, проведенной в точку касания, по касательной и наоборот			№641, 643, 648
54			Центральный угол	УОНМ	Центральные и вписанные углы. Градусная мера дуги окружности	Знать: понятие градусной меры дуги окружности, понятие центрального угла. Уметь: решать простейшие задачи на вычисление градусной меры дуги окружности	УО		п. 70 № 649 б, г, 650 б, 651 б, 652
55			Теорема о вписанном угле	УОНМ	Понятие вписанного угла. Теорема о вписанном угле и следствия из нее	Знать: определение вписанного угла, теорему о вписанном угле и следствия из нее. Уметь: распознавать на чертежах вписанные утлы, находить величину вписанного угла	Проверка домашнего задания		п. 71 № 654 б, г, 655,657, 659
56			Теорема об отрезках пересекающихся хорд	КУ	Теорема об отрезках пересекающихся хорд	Знать: формулировку теоремы, уметь доказывать и применять ее при решении задач, выполнять чертеж по условию задачи	Текущий		№ 666 б, в, 671 б, 660, 668
57			Решение задач	КУ	Центральные и вписанные углы	Знать определения центрального и вписанного углов, теоремы об отрезках пересекающихся хорд. Уметь находить величину центрального и вписанного углов	СР 27 дм 15 мин		№661,663 PTN°90, 91
58			Свойство биссектрисы угла	УОНМ	Теорема о свойстве биссектрисы угла	Знать формулировку теоремы о свойстве равноудаленности каждой точки биссектрисы угла и этапы ее доказательства. Уметь: находить элементы треугольника, используя свойство биссектрисы; выполнять чертеж по условию задачи	ФО	Окружность Эйлера	№ 675, 676 б, 678 б, 677
59			Серединный перпендикуляр	КУ	Понятие серединного перпендикуляра, теорема о серединном перпендикуляре	Знать понятие серединного перпендикуляра, формулировку теоремы. Уметь: доказывать и применять теорему для решения задач на нахождение элементов треугольника	Теор. опрос		679 б, 680 б,681 РТ № 102
60			Теорема о точке пересечения высот треугольника	КУ	Теорема о точке пересечения высот треугольника, четыре замечательные точки треугольника	Знать четыре замечательные точки треугольника. Формулировку теоремы о пересечении высот треугольника. Уметь: находить элементы треугольника	СР № 29 ДМ (15 мин)		СР № 28 ДМ
61			Вписанная окружность	УОНМ	Понятие вписанной окружности. Теорема об окружности, вписанной в треугольник	Знать: понятие вписанной окружности, теорему об окружности, вписанной в треугольник. Уметь: распознавать на чертежах вписанные окружности, находить элементы треугольника, используя свойства вписанной окружности			п. 74 № 689, 692, 693 б, 694
62			Свойство описанного четырехугольника	КУ	Теорема о свойстве описанного четырехугольника	Знать: теорему о свойстве описанного четырехугольника и этапы ее доказательства. Уметь: применять свойство описанного четырехугольника при решении задач, выполнять чертеж по условию задачи	Проверка до-машне-го задания. УО		№ 695, 699, 700, 701
63			Описанная окружность	УОНМ	Описанная окружность. Теорема об окружности, описанной около треугольника	Знать: определение описанной окружности, формулировку теоремы об окружности, описанной около треугольника. Уметь: проводить доказательство теоремы и применять ее при решении задач, различать на чертежах описанные окружности	УО		п. 75 № 702 б, 705 6,711
64			Свойство вписанного четырехугольника	КУ	Свойство углов вписанного четырехугольника	Знать: формулировку теоремы о вписанном четырехугольнике. Уметь: выполнять чертеж по условию задачи, решать задачи, опираясь на указанное свойство	МД№4 ДМ (20 мин)		№705, 710, 735
65			Решение задач по теме «Окружность»	УОСЗ	Вписанная и описанная окружности. Вписанные и описанные четырехугольники	Знать: формулировки определений и свойств. Уметь: решать простейшие геометрические задачи, опираясь на изученные свойства	ФО		№ 726, 728, 734
66			Решение задач по теме «Окружность»	КУ	Вписанная и описанная окружности. Вписанные и описанные четырехугольники	Знать: формулировки определений и свойств. Уметь: решать простейшие геометрические задачи, опираясь на изученные свойства	Проверка домаш-него задания, задач для самостоятельного решения		№722,731, 707
67			Контрольная работа № 5 «Окружность»	УКЗУ	Контроль и оценка знаний и умений	Уметь: находить один из отрезков касательных, проведенных из одной точки по заданному радиусу окружности; находить центральные и вписанные углы по отношению дуг окружности; находить отрезки пересекающихся хорд окружности, используя теорему о произведении отрезков пересекающихся хорд	КР№5 ДМ (40 мин)		Повторить главу «Четырехугольники»
68			Анализ контрольной работы. Повторение темы «Четырехугольники»	УОСЗ	Четырехугольники: определения, свойства; признаки, площадь	Знать: формулировки определений, свойств, признаков: параллелограмма, ромба, трапеции. Уметь: находить элементы четырехугольников, опираясь на изученные свойства, выполнять чертеж по условию задачи; вычислять площадь четырехугольника	УО

Пояснительная записка

Планирование составлено с учётом примерной программы основного общего образования по математике и скорректирована на её основе программа: «Геометрия 7-9» авторы Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина.

Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Геометрия – один из важнейших компонентов математического образования. Она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции, математической культуры, эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Программа направлена на достижение следующих целей:

§ овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;

§ интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений;

§ формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

§ воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;

§ развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.

В курсе геометрии 8-го класса продолжается решение задач на признаки равенства треугольников, но в совокупности с применением новых теоретических факторов. Теореме о сумме углов выпуклого многоугольника позволяет расширить класс задач. Формируется практические навыки вычисления площадей многоугольников в ходе решения задач. Особое внимание уделяется применению подобия треугольников к доказательствам теорем и решению задач. Даются первые знания о синусе, косинусе и тангенсе острого угла прямоугольного треугольника. Даются учащимся систематизированные сведения об окружности и её свойствах, вписанной и описанной окружностях. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.

Программой отводится на изучение геометрии по 3 урока в неделю, что составляет 105 часов в учебный год. Из них контрольных работ 6 часов, которые распределены по разделам следующим образом: «Четырехугольники» 1 час, «Площадь» 1 час, «Подобие треугольников» 2 часа, «Окружность» 1 час и 1 час отведен на итоговую административную контрольную работу.

Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.

Количество часов по темам изменено в связи со сложностью тем.

Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде административной контрольной работы.

Домашнее задание описано на блок уроков. По ходу работы, в зависимости от темпа прохождение материала номера заданий распределяются по урокам так, что по окончании изучения блока все задания выполнены учащимися в обязательном порядке.

Уроки геометрии интегрируются с информатикой. Доказательство геометрических фактов ведется в среде математическое лаборатории Живая математика.

Требования к уровню подготовки учащихся.

В результате изучения курса геометрии 8-го класса учащиеся должны уметь:

§ пользоваться геометрическим языком для описания предметов окружающего мира;

§ распознавать геометрические фигуры, различать их взаимное расположение;

§ изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;

§ вычислять значения геометрических величин (длин, углов, площадей), в том числе: определять значение тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;

§ решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;

§ проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

§ решать простейшие планиметрические задачи в пространстве.

Сокращения, используемые в рабочей программе:

Типы уроков	Виды контроля
УОНМ — урок ознакомления с новым материалом	ФО — фронтальный опрос
УЗИМ — урок закрепления изученного материала	ИРД — индивидуальная работа у доски.
УПЗУ — урок применения знаний и умений	ИРК — индивидуальная работа по карточкам
УОСЗ — урок обобщения и систематизации знаний.	СР — самостоятельная работа
УПКЗУ — урок проверки и коррекции знаний и умений	ПР — проверочная работа
КУ — комбинированный урок	МД — математический диктант
	Т – тестовая работа
	КР - контрольная работа

ГРАФИК КОНТРОЛЬНЫХ РАБОТ

1 четверть

Контрольная работа №1 по теме «Четырёхугольник».

2 четверть

Контрольная работа №2 по теме «Площадь».

3 четверть

Контрольная работа №3 по теме «Признаки подобия треугольников».

Контрольная работа №4 по теме «Применение подобия треугольников, соотношение между сторонами и углами прямоугольного

треугольника».

4 четверть

Контрольная работа №5 по теме «Окружность»

Контрольная работа №6 по теме «Повторение курса геометрии за 8 класс».

Приложение

Контрольная работа №1

Четырехугольники

Вариант 1

1. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол между диагоналями, если

2. В параллелограмме KMNP проведена биссектриса угла MKP, которая пересекает сторону MN в точке Е.

а) Докажите, что треугольник КМЕ равнобедренный.

б) Найдите сторону КР, если МЕ = 10 см, а периметр параллелограмма равен 52 см.

Контрольная работа №1

Четырехугольники

Вариант 1

1. Диагонали ромба КМNP пересекаются в точке О. Найдите углы треугольника КМО, если

2. На стороне ВС параллелограмма ABCD взята точка M так, что АВ = ВМ.

а) Докажите, что АМ – биссектриса угла ВАD.

б) Найдите периметр параллелограмма, если CD = 8 см, СМ = 4 см.

8 Контрольная работа №2

Площадь

Вариант 1

1. Смежные углы параллелограмма равны 32 см и 26 см, а один из его углов равен 150^о. Найдите площадь параллелограмма.

2. Площадь прямоугольной трапеции равна 120 см², а её высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.

3. На стороне АС данного треугольника АВС постройте точку D так, чтобы площадь треугольника АВD составила одну треть площади треугольника АВС.

Контрольная работа №2

Площадь

Вариант 2

1. Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см².

2. Найдите площадь трапеции АВСD с основаниями АD и ВС, если известно, что АВ = 12 см, ВС = 14 см, АD = 30 см,

3. На продолжении стороны KN данного треугольника KMN постройте точку Р так, чтобы площадь треугольника NMР была в два раза меньше площади треугольника KMN.

Контрольная работа №3

Подобные треугольники

Вариант 1

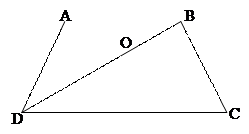1. На рисунке АВ║СD.

а) Докажите, что АО : ОС = ВО : ОD.

б) Найдите АВ, если ОD = 15 см, ОВ = 9 см, СD = 25 см.

2. Найдите отношение площадей треугольников АВС и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, КМ = 10 см, МN = 15 см, NK = 20 см.

Контрольная работа №3

Подобные треугольники

Вариант 2

1. На рисунке MN║АС.

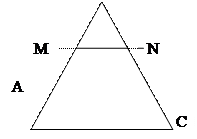а) Докажите, что АВ ^.BN = CВ ^. BM.

б) Найдите MN, если AM = 6 см, ВM = 8 см, AС = 21 см.

2. Даны стороны треугольников PQR и АВС: PQ = 16 см, QR = 20 см, PR = 28 см, АВ = 12 см, ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.

8 Контрольная работа №4

Соотношения между сторонами и углами в прямоугольном треугольнике

Вариант 1

1. В прямоугольном треугольнике АВС высота АD равна 12 см. Найдите АС и cos C.

2. Диагональ ВD параллелограмма АВСD перпендикулярна к стороне АD. Найдите площадь параллелограмма АВСD, если АВ = 12 см,

Контрольная работа №4

Соотношения между сторонами и углами в прямоугольном треугольнике

Вариант 2

1. Высота ВD прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок DC, равный 18 см. Найдите АВ и cos A.

2. Диагональ АС прямоугольника АВСD равна 3 см и составляет со стороной АD угол 37^о. Найдите площадь прямоугольника АВСD.

Контрольная работа № 5

Окружность

Вариант 1

1. Через точку А окружности проведены диаметр АС и две хорды АВ и АD, равные радиусу этой окружности. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.

2. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Контрольная работа № 5

Окружность

Вариант 2

1. Отрезок ВD – диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.

2. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Итоговая контрольная работа

Вариант 1

1. В трапеции АВСD точка М – середина большего основания АD, МD = ВС, Найдите углы АМС и ВСМ.

2. На стороне АD параллелограмма АВСD отмечена точка К так, что АК = 4 см, КD = 5 см, ВК = 12 см. Диагональ ВD равна 13 см.

а) Докажите, что треугольник ВКD прямоугольный.

б) Найдите площади треугольника АВК и параллелограмма АВСD.

3. Отрезки АС и ВD пересекаются в точке О, причем АО = 15 см, ВО = 6 см, СО = 5 см, DO = 18 см.

а) Докажите, что четырехугольник АВСD – трапеция.

б) Найдите отношение площадей треугольников АОD и ВОС.

4. Около остроугольного треугольника АВС описана окружность с центром О. Расстояние от точки О до прямой АВ равно 6 см, Найдите: а) угол АВО; б) радиус окружности.

Итоговая контрольная работа

Вариант 1

1. В трапеции АВСD на большем основании АD отмечена точка М так, что АМ = 3 см, СМ =- 2 см, , Найдите длины сторон АВ и ВС.

2. В трапеции АВСD FD = 8 см, DC = 4 см, CD = 10 см. Найдите:

а) найдите площадь треугольника АСD;

б) площадь трапеции АВСD.

3. Через точку М стороны АВ треугольника АВС проведена прямая, перпендикулярная высоте ВD треугольника и пересекающая сторону ВС в точке К. Известно, что ВМ = 7 см, ВК = 9 см, ВС = 27 см. Найдите:

а) длину стороны АВ;

б) отношение площадей треугольников АВС и МВК.

4. В треугольник АВС с прямым углом С вписана окружность с центром О, касающаяся сторон АВ, ВC и СА в точках D, Е и F соответственно. Известно, что . Найдите: а) радиус окружности; б) углы ЕОF и ЕDF.

Литература:

1.Артюнян Е. Б., Волович М. Б., Глазков Ю. А., Левитас Г. Г. Математические диктанты для 5-9 классов. – М.: Просвещение, 2004.

2.Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия 7-9. – М.: Просвещение, 2006.

3.Буланова Л. М., Дудницын Ю. П. Проверочные задания по математике для учащихся 5-8 и 10 классов. – М.: Просвещение, 2006.

4.Зив Б. Г., Мейлер В. М. Дидактические материалы по геометрии за 8 класс. – М.: Просвещение, 2005.

5.Иченская М. А. Самостоятельные и контрольные работы к учебнику Л. С. Атанасяна 7-9 классы. – Волгоград: Учитель, 2006.

Свойства и признаки равнобедренной трапеции

Контрольная работа № 1 по теме: «Четы рехугольники»

Решение задач по те ме: «Признаки подо бия треугольников»

Контрольная работа № 4 «При менение подобия тре угольников, соотношения между сторонами и углами пря моугольного треугольника»

В курсе геометрии 8-го класса продолжается решение задач на признаки равенства треугольников, но в совокупности с применением новых теоретических факторов

Даются первые знания о синусе, косинусе и тангенсе острого угла прямоугольного треугольника

Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала

Сокращения, используемые в рабочей программе:

У П ЗУ — урок применения знаний и умений

Вариант 2 1. Одна из диагоналей параллелограмма является его высотой и равна 9 см

Контрольная работа №3 Подобные треугольники

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также