РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ

Разложение на множители
с помощью формул квадрата суммы и разности

Цели: показать, как применяются формулы квадрата суммы и квадрата разности при разложении на множители трехчленов; формировать умение выполнять данное действие.

Ход урока

I. Устная работа.

1. Выполните возведение в квадрат.

а) (х – 2)²;          б) (2 + х)²;                   в) (–х + 2)²;                        г) (–х – 2)².

2. Будут ли тождественно равны следующие выражения:

а) (а – 2)² и (2 – а)²;                                                              в) (3 – с)² и (–с + 3)²;

б) (х – 1)² и (1 + х)²;                                               г) (–у – 5)² и (у + 5)²?

3. Представьте выражение в виде квадрата одночлена.

а) 25а²;                               в) y²;                    д) 2,25т⁴;

б) 121х²;                             г) 0,64с⁴;                      е) n⁶.

II. Объяснение нового материала.

1.– Что значит «разложить на множители многочлен»?

– Какие вы знаете способы разложения многочлена на множители?

– При решении каких задач пригодится умение раскладывать многочлен на множители?

2. Познакомимся с ещё одним способом разложения многочлена на множители. Этот способ состоит в применении формул квадрата суммы и разности.

3. выводы:

1) с помощью формул квадрата суммы и разности можно раскладывать на множители только трёхчлены;

2) чтобы трёхчлен раскладывался на множители, два его члена должны являться квадратами некоторых одночленов, а третий член должен быть удвоенным произведением этих одночленов.

III. Формирование умений и навыков.

1. № 833, № 834.

Пример:               .

Проверка:        

Затем проверку можно будет делать устно.

2. № 836, № 837.

№ 836.

Решение:

а) * + 56а + 49.

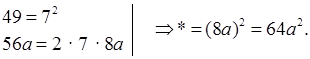
б) 36 – 12х + * .

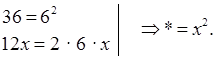
в)

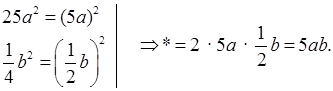
г) 0,01b² + * + 100c².

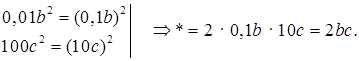
3. № 839 (а, в, г).

Перед выполнением этого номера следует привести пример.–х² + 2х – 1 = –(х² – 2х + 1) = –(х – 1)².

Решение:

а) –1 + 4а – 4а² = –(1 – 4а + 4а²) = – (1 – 2а)²;

в) 24 ab – 16a² – 9b² = –(16a² – 24 ab + 9b²) = – (4a – 3b)²;

г) –44ах + 121а² + 4х² = (11а – 2х)².

4. № 840 (б).

Решение:

4х² – 20х + 25 = (2х – 5)²

при х = 12,5:              (2х – 5)² = (25 – 5)² = 400;

при х = 0:    (2х – 5)² = (0 – 5)² = 25;

при х = –2: (2х – 5)² = (–4 – 5)² = 81.

IV. Итоги урока.

– Какие существуют способы разложения многочлена на множители?

– Какие многочлены могут быть разложены на множители с помощью формул квадрата суммы и разности?

– Можно ли разложить на множители следующие трёхчлены:

а) х² – 6х + 9;                                            в) а² – 2а – 1;

б) х² + 4х + 6;                                            г) 4т² – 4т + 1?

Домашнее задание: № 835; № 838; № 839 (б, д, е); 840 (в).