Разноуровневые контрольные работы по алгебре 9 класс

                                               

 

        Дифференцированный подход  на уроках математики.

                      Разноуровневые контрольные работы

        Варианты контрольных работ для учащихся 9-х классов, которые включают в себя задания 2-х уровней.

 Выполнение 1 и 2 варианта  рассчитано на удовлетворительный результат, для поднятия оценки достаточно решения задания обозначенного *.  Следовательно, выполнение 3 и 4 вариантов оценивается на «отлично».

 

 Контрольная работа №1 по теме «Квадратичная функция.»

                                              Уровень «А»

 Вариант 1.

1.Разложите на множители квадратный трехчлен:

а) х²-14х+45;  в)3у²+7у-6

2.Постройте график функции у=х²-2х-8.Найдите с помощью графика:

А) значение у, при х=-1,05;

Б) значения х, при которых у=3;

В) нули функции;

Г) промежуток,  в котором функция возрастает.

3.Сократите дробь:     3р²+р-2

                                         4-9р²

4^*.Не выполняя построение, определите, пересекаются ли парабола  у=1 -3х²         и                                                                                                          

прямая у=6х-15. Если точки пересечения существуют , то найдите их координаты.

                  Вариант 2

1.Разложите на множители квадратный трехчлен:

а) х²-10х+21;   в)5у²+9у-2

2.Постройте график функции у=х²-4х-5.Найдите с помощью графика:

А) значение у, при х=0,5;

Б) значения х, при которых у=3;

В) нули функции;

Г) промежуток, в котором функция убывает.

3.Сократите дробь:     4с²+7с-2

                                         1-16с²

4^*.Не выполняя построение, определите, пересекаются ли парабола у=    1-   2х²     и прямая  у=12-х, если точки пересечения существуют, то найдите их координаты.

 

                                                                   

 

                                                            Уровень «В»

Вариант 3.

1.Докажите, что данные два квадратные трехчлена имеют общий корень и найдите его:14х²+19х-3 и  -14х²+37х-5.

2.Постройте график функции и укажите на нем все точки, координаты которых удовлетворяют данному условию. Найдите координаты этих точек: у=х²-4х+4, абсцисса равна ординате.

3.Сократите дробь и вычислите её значение при х=х₀:  -15х²+13х-2

                                                                                               3х²-8х+4       , х₀=4,2

4.Пусть f(x)= х²-6х+9  _  х²-8х+16,    найдите f(5/9)

               3-х

5^*.При каких значениях  а график данной функции проходит через данную точку k:  у = aх²-5х-3,k(-1;3).

 

Вариант 4.

1.Докажите, что данные два квадратные трехчлена имеют общий корень и найдите его: -15х²+4х+4 и  15х²+х-2.

2.Постройте график функции и укажите на нем все точки , координаты которых удовлетворяют данному условию. Найдите координаты этих точек: у=х²+2х+2, сумма абсциссы и ординаты равна нулю.

3.Сократите дробь и вычислите её значение при х=х₀:  -15х²+13х-2

                                                                                               3х²-8х+4       , х₀=4,2

4.Пусть f(x)= х²-4х+4  _  х²-8х+16,    найдите f(3/7)

                                 4-x

5^*.При каких  значениях  а график данной функции проходит через данную точку k:  у = 3х²-ах-1, k(-2;1).

 

 

                                       

Контрольная работа №2 по теме «Неравенства второй степени с одной переменной».

Вариант №1.

1.Решить неравенство:

А) 2х²-13х+6<0 ; б) х²-9>0  в) 3х²-6х+32>0

2.Решить неравенство используя метод интервалов:

А) (х+8)(х-4)>0   Б)    <0

3. Дана функция у =

Найдите область её определения.

4*.При каких значениях t уравнение  3х²+tх+3=0 имеет два корня?

 

Вариант 2

1.Решить неравенство:

А) 2х²-х-15 >0 ; б) х²-16<0  в) х²+12х+8<0

2.Решить неравенство, используя метод интервалов:

А) (х+8)(х-4)<0   Б)    >0

3. Дана функция у =

Найдите область её определения.

4*.При каких значениях t уравнение  2х²+tх+8=0  не имеет  корней?

Вариант 3

1.Решите неравенство:

а) х²-5х-6 >0 ; б) 4х² ≤ х

2.Дана функция  f(х)=6х-х²   найдите при каких значениях х,  f(х)>0, f(х)≤0.

3.Решите неравенство используя метод интервалов:

а) х(х-1)(х+2)<0  б)    ≥0   в)<1.

4. При каких значениях в определено выражение  +

5. При каких значениях параметра  а  уравнение 3х²+ах+а-3=0  имеет два различных корня?

 

Вариант 4

1.Решите неравенство :

а) х²+2х-12 <0 ; б) х²≥ 25

2.Дана функция  f(х)=х²-2х найдите при каких значениях х,  f(х)≥0, f(х)<0.

3.Решите неравенство используя метод интервалов:

а) х(х+1)(х-3)>0  б)    ≤0   в)>1.

4. При каких значениях в определено выражение  +

5. При каких значениях параметра  а  уравнение 4х²+ах+а-4=0  имеет два различных корня?

Контрольная работа №3 по теме «Целое уравнение и его корни»

Вариант 1.

  1.Решите уравнение:

а) х³-25х=0 ;       б)  - -=1

2. Решите биквадратное уравнение :  х⁴-4х²-45=0

3.Решите уравнение используя введение новой переменной :

а) (х²-7)²-4(х²-7)-45=0;   б)  (х²-х+1)( х²-х-7)=65.

4*. При каких значениях параметра  а  уравнение имеет один корень:

 х⁴-6х²+а=0.

Вариант 2.

1.Решите уравнение:

а) х³-81х=0 ;       б)  - -=2

2. Решите биквадратное уравнение :  х⁴-19х²+48=0

3.Решите уравнение используя введение новой переменной :

а)(х²-10)²-3(х²-10)+4=0   ;   б)  (х²+х+6)( х²+х-4)=144.

4*. При каких значениях параметра а  уравнение имеет один корень:

 х⁴-8х²+а=0.

 

Вариант 3.

1.решите уравнение:

(1-2х)(4х²+2х+1)=(2-2х)(4+4х)(х+2)

2.Решите уравнение указанным способом:

а)  замена переменной:     2()²-7+5=0,

б)   разложите на множители:  )²-1=0

в) х⁴-9х²+18=0.

3*.  При каких значениях параметра а  уравнение имеет один корень:

ах²- (2а+6)х+3а+3=0.

 

Вариант 4.

1.решите уравнение:

(8х-16)(х2-1)=(4х²-2х+1)(2х+1)

2.Решите уравнение указанным способом:

а) замена переменной     5()²-7-3=0,

б) разложите на множители     )² –=0

в) х⁴+3х²-10=0.

3*. При каких значениях параметра а  уравнение имеет  два различных корня:

ах²+(4а-2)х +=0.

²-8=0

Контрольная работа №4 по  теме: « Системы уравнений»

Вариант 1.

1.Решите систему уравнений:

2.Периметр прямоугольника равен 28 м, а его площадь равна 40 м². Найдите стороны прямоугольника.

3. Не выполняя построения найдите координаты точек пересечения параболы у=х²+4  и  прямой х+у=6.

4.*Решите систему уравнений

Вариант 2.

1.Решите систему уравнений:

2.одна из сторон прямоугольника на 2 см  больше другой стороны .Найдите стороны прямоугольника , если его площадь равна 120 см².

3. Не выполняя построения найдите координаты точек пересечения параболы у=х²-8  и  прямой х+у=4.

4.*Решите систему уравнений

 

Вариант 3.

1.Решите систему уравнений :

2.Басейн заполняется водой ,поступающей через две трубы. Одна труба может заполнить бассейн за 12 часов , а другая за 20 часов. За сколько часов заполниться бассейн работая одновременно ?

3.Решите графически систему уравнений :

4*.Решите систему уравнений: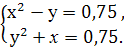

Вариант 4.

1.Решите систему уравнений:

2.Вода , поступающая в первую трубу , может заполнить бассейн за 6 ч. , а вода , вытекающая из второй трубы , может его опорожнить за 15 ч.За сколько часов наполниться бассейн , если обе трубы будут одновременно открыты ?

3.Решите графически систему уравнений:

4*.Решите систему уравнений: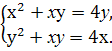

 

Контрольная работа №5 по теме: « Арифметическая прогрессия».

Вариант 1.

1.Найдите  а₄₅  арифметической прогрессии  (а_n), если а₁=65, d=-2.

2.Найдите S₂₄  арифметической прогрессии: 42; 34; 26;…

3.Является ли число 6,5 членом арифметической прогрессии (а_n), в которой а₁= 2,25 и а₁₁=10,25 ?

4*.Найдите сумму членов  с третьего по десятый включительно арифметической прогрессии: -3; -1; …

Вариант 2.

1.Найдите  а₃₂  арифметической прогрессии  (а_n), если а₁=-9, d=4.

2.Найдите S₁₄  арифметической прогрессии : -63; -58; -33…

3.Является ли число 35,8 членом арифметической прогрессии(а_n), в которой а₁= 23,6 и а₂₂=11 ?

4*.Найдите сумму членов  с третьего по десятый включительно арифметической прогрессии: 2; 7; …

Вариант 3.

1.В арифметической прогрессии (а_n) а₁=8 ,а₁₁=104, d=3.Найдите  n и S_n.

2. В арифметической прогрессии (а_n) d=-7, n=-149.Найдите а₁ и  S_n.

3. В арифметической прогрессии 59; 55; 51; …  найдите сумму всех её положительных членов.

4*.Найдите седьмой член арифметической прогрессии, если а₃+ а_n=20.

Вариант 4.

1.В арифметической прогрессии (а_n) а₁=5 ,а_n=509, n =100.Найдите d  и S_n.

2. В арифметической прогрессии (а_n) d=3, n=15, а_n=50.Найдите а₁ и  S_n.

3. В арифметической прогрессии -63; -58; -53; …  найдите сумму всех её отрицательных членов.

4*.Запишите формулу n-го члена  и суммы n первых членов арифметической  прогрессии  (а_n) , если а₂*а₅=112,  .

 

Контрольная работа №6 по теме: «Геометрическая прогрессия»

Вариант 1.

1.Найдите в₉ геометрической прогрессии (в_{n) ,} если в₁=-32 и g=1/2.

2. Найдите S₆ геометрической прогрессии, если в₁=2 и q=3.

3. Найдите сумму бесконечной геометрической прогрессии: 24; -12; 6

4. Представьте в виде обыкновенной дроби десятичную дробь

а)0,(27); в) 0,5(6)

5*.Найдите отношение суммы бесконечной геометрической прогрессии к сумме квадратов её членов, если в₂=2 и q=-1/2.

 

Вариант 2.

1.Найдите в₆ геометрической прогрессии (в_{n) ,} если в₁=0,81 и g=-1/3.

2. Найдите S₇ геометрической прогрессии , если в₁=6 и q=2.

3. Найдите сумму бесконечной геометрической прогрессии: -40; 20; -10;…

4. Представьте в виде обыкновенной дроби десятичную дробь

а)0,(153); в) 0,03(2)

5*.Найдите отношение суммы бесконечной геометрической прогрессии к сумме  её членов с нечетными номерами, если в₁=3 и q=1/3.

 

Вариант 3.

1.В геометрической прогрессии (в_n) : в₁=2, в_n=1024, S_n=2046.Найдите q  и  n.

2. В геометрической прогрессии ( в_n): в₁=0,5, в_n=256,q=2.  Найдите     n   и  S_n.

3. Найдите сумму членов с третьего по шестой включительно  геометрической прогрессии : 1/16 ; 1/8;…

4.В бесконечной геометрической прогрессии в₂=0,3 ; в₃=-0,2.Найдите сумму этой прогрессии.

5*. Напишите формулу  n-го члена  и суммы  n- первых членов геометрической прогрессии, если  в₃- в₂=12 ,   2в₃+ в₄=96.

 

Вариант 4.

1.В геометрической прогрессии (в_n): в₁=512, в_n=1,S_n=1023.Найдите q  и  n.

2. В геометрической прогрессии (в_n): в₁=80, в_n=5,q=0,5.  Найдите     n   и  S_n.

3. Найдите сумму членов с третьего по шестой включительно  геометрической прогрессии : 32 ; 16;…

4.В бесконечной геометрической прогрессии в₂=24; S=108.Найдите  в₁ и q..

5*. Напишите формулу  n-го члена  и суммы  n- первых членов геометрической прогрессии, если  в₃*в₄=27 ,   в₁₉/ в₁₇=9.