Разработка

Дата:____________Проверила:______________

Учитель:  .

1.Класс -9

Тема: Решение текстовых задач алгебраическим способом

2.Тип урока:Урок систематизации знаний и умений

3.Планируемые результаты:

Личностные: Овладение языковой и читательской культурой как средством познания мира.

Овладение основными навыками исследовательской деятельности, установка на осмысление опыта, наблюдений, поступков и стремление совершенствовать пути достижения индивидуального и коллективного благополучия.

Готовность к разнообразной совместной деятельности, стремление к взаимопониманию и взаимопомощи, активное участие в школьном самоуправлении

Предметные:Решать текстовые задачи с помощью уравнений, неравенств и их систем, интерпретировать полученные результаты, проводить отбор решений исходя из смысла величин, данных в условии задачи

Метапредметные :выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями, формулировать определения понятий, устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа;

*воспринимать, формулировать и преобразовывать суждения: утвердительные и отрицательные, единичные, частные и общие, условные;

*выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях, предлагать критерии для выявления закономерностей и противоречий;

*делать выводы с использованием законов логики, дедуктивных и индуктивных умозаключений, умозаключений по аналогии;

Ключевые слова: РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ АЛГЕБРАИЧЕСКИМ СПОСОБОМ

Краткое описание:  На уроке предусмотрено использование следующих типов электронных образовательных материалов: «Диагностическая работа», «Самостоятельная работа».

Блочно-модульное описание урока

БЛОК1. Вхождение  в тему урока и создание условий для осознанного восприятия нового материала.

1.Мотивирование на учебную деятельность

Девиз нашего урока

«Мудрым никто не родился, а научился»

- Как понимаете эти слова?

- Сегодня продолжим путь к мудрости

- С чего начнем?

2.. Актуализация опорных знаний

Начнем с разминки..

1.         Собственная скорость катера 23,4 км/ч. Скорость течения реки 3,9. Найдите скорость катера по течению и против течения. (27,3км/ч и 19,5 км/ч)

2.    Найдите 5% от числа 80. (4)

3.         Периметр квадрата 4,8 см. Найдите его сторону и площадь. (1,2 см и 1, 44 см²)

4.         Какой путь пройдет турист со скоростью 4,5 км/ч за 4 часа? (18 км)

5.         За 45 минут мастер изготовил 15 деталей. Сколько деталей изготовит мастер за час? (20)

3. Целеполагание

(Назовите цель: ты узнаешь, ты научишься) Наша задача рассмотреть такие виды задач как задачи на движение, обратить внимание на схематизацию и моделирование условия; выработать основные этапы решения текстовых задач; а основная цель нашего урока – это подготовка к успешной сдачи экзамена.

БЛОК 2. Освоение нового материала

1.Осуществление учебных действий по освоению нового материала

На этом уроке мы разберем задачи на движение

Для решения задач на движение нужно помнить формулу:

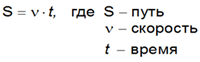
Так же важно знать и формулу для нахождения средней скорости:

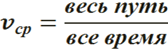
            Существует 3 вида задач на движение: движение двух объектов навстречу друг другу, движение в противоположных направлениях, движение в одном направлении.

Полезно запомнить:

Если два тела начинают движение одновременно или догоняют друг друга, то до встречи они затрачивают одинаковое время.

При прохождении одного и того же пути, если тела начинают движение в разное время, то, которое выходит раньше затрачивает времени больше.

Задачи на встречное движение двух тел.

Пусть движение первого тела характеризуется величинами s1, v1, t1; движение второго - s2, v2, t2.

Формулы:  t₁= t₂= t встр.,   v сбл.= v₁+ v₂ ,    S= v сбл * tсбл..

Из двух сел одновременно выехали навстречу 2 велосипедиста. Скорость одного из них 24 км/ч, а другого – 18 км/ч. Найдите расстояние между селами, если  велосипедисты встретились через три часа.

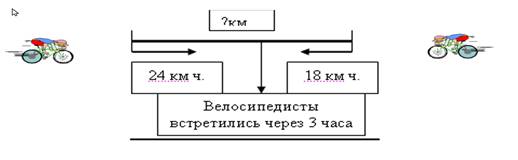
Решение: 3*х(24 +18) =126 (км)

Ответ: 126 км.

Задачи на движение двух тел в одном направлении.

Среди них следует различать два типа задач:

1) движение начинается одновременно из разных пунктов;

2) движение начинается в разное время из одного пункта.

Формулы: v₁>v₂,  v сбл.= v₁- v₂,     S = s₁– s₂и  S = v сбл * tвстр.

Из одного пункта в одном направлении одновременно выехали две автомашины. Скорость первой машины 40 км/ч, а второй в 2 раза больше. Какое расстояние будет между ними через 2 часа?

Решение:160-80=80 (км)

Ответ: 80 км.

Задачи на движение двух тел в противоположных направлениях.

В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки:

 1) одновременно;  2) в разное время.

А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.      Формулы: v удал. = v₁+ v₂

Из одного пункта в противоположных направлениях вышли два лыжника. Один идет со скоростью 18 км/ч, а другой со скоростью 7 км/ч. Через какое время расстояние  между лыжниками будет равно 75 км?

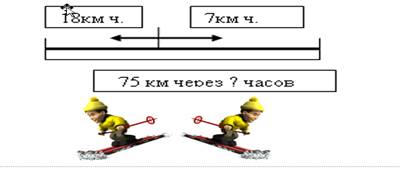
Решение: 75: (18 +7) =3 (ч)

Ответ: через 3 часа.

Задачи на движение протяженных тел

В задачах на движение протяжных тел требуется определить длину одного из них. Наиболее типичные ситуации: определение длины поезда проезжающего мимо

•          Платформы (придорожного столба, лесополосы определенной длины и т.д.);

•          идущего параллельно путям пешехода;

•          другого двигающегося поезда.

Если поезд движется мимо столба, то он проходит расстояние равное его длине.

1.Поезд, двигаясь со скоростью 70км/ч, проезжает мимо платформы за 45сек. Определите длину платформы ( в метрах), если длина поезда 600м.

Решение:

45 сек=45/3600=1/80часа:  600м=0,6км:  х - длина платформы

(0,6+х)/70=1/80

48+80х=70

х=22/80

х=0,275км=275м   Ответ: 275 км

2.Поезд, двигаясь равномерно со скоростью 148 км/ч,  проезжает мимо пешехода,  идущего в том же направлении параллельно путям со скоростью 4 км/ч, за 10 секунд. Найдите длину поезда в метрах.

148-4=144/ч - скорость поезда относительно движущегося человека

10 сек=10/3600=1/360 ч

144х1/360=144/360=0,4 км=400 м     Ответ:  400 м

Задачи на движение по воде

2.Проверка первичного закрепления

Решите задачи. Краткое решение и ответ впишите в соответствующие окошки в рабочих листах.

Автомобиль ехал 1,5 часа со скоростью 40км/ч, 2,5 часа – со скоростью 60км/ч, а оставшуюся часть пути со скоростью 75км/ч. Определите среднюю скорость автомобиля, если на весь путь он потратил 5часов.

РЕШЕНИЕ:

1)40 ·1,5=60(км) –путь за 1, 5часа

2)60·2,5=150(км) путь за 2,5ч

3) 5– ( 1,5+2,5)=1(ч) оставшееся время

4) 75·1=75(км) оставшийся путь.

5) 60+150+75=285(км) весь путь

6)285:5=57(км/ч) –средняя скорость на всем пути.

Первые 360 км автомобиль ехал со скоростью 60 км/ч, следующие 180 км  - со скоростью  90км/ч, а затем 200км – со скоростью100км/ч.  Найти  среднюю скорость автомобиля на протяжении всего пути.

РЕШЕНИЕ:

Среднюю скорость найдем по формуле Vсредняя =Sвесь:tвсего пути

1 ) 360+180+200 =740(км)-весь путь

2 )360:60+180:90+200:100=10(ч) время всего пути

3 )740:10=74км/ч средняя скорость.

Ответ: 74км/ч

БЛОК 3.  Применение изученного  материала

1.Применение знаний,  в том числе в новых ситуациях

Самостоятельная работа

Два грузовика отправляются с завода до места назначения, расстояние между которыми равно 510 км. Первый идет со скоростью на 10 км/ч больше, чем второй, и прибывает к месту назначения на 1 ч 42 мин раньше второго. Найдите скорость второго грузовика.

РЕШЕНИЕ:

Пусть скорость второго грузовика х км/ч, тогда 510 км он проедет за 510/х часов. Скорость первого грузовика (х + 10) км/ч, и 510 км он проедет за 510/(х + 10) часов.

 1ч 42 мин = 142/60=17/10  ч.

Составим и решим уравнение:

510/х-510/(х+10)=17/10,    х^2+10х-3000=0,   х1= 50,  х2=-60.

Ответ: 50 км/ч.

      2.Задание ЕГЭ и ОГЭ

По двум параллельным железнодорожным путям в одном направлении следует электропоезд и товарный поезд, скорости которых равны соответственно 55 км/ч и 25 км/ч. Длина товарного поезда равна 1600 метрам. Найдите длину электропоезда, если время, за которое он прошел мимо товарного поезда,  равно 4,5 минуты.

РЕШЕНИЕ:

55 – 25= 30 км/ч= 500 м/мин – относительная скорость поездов.

500*4,5 = 2250 м – суммарная длина поездов.

2250 – 1600 = 650 м.

Ответ: 650м

Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 60 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 40 минут позже автомобилиста. Ответ дайте в км/ч.

РЕШЕНИЕ:

Пусть х км/ч скорость велосипедиста, тогда скорость автомобилиста (х+60) км/ч .

2ч 40мин. =8/3часа. 

50/х – 50/(х+60) = 8/3,

150(х+60) – 150х=8х(х+60),

8х² +480х– 9000=0,

х² +60х– 1125=0 ,

х₁=15, х₂ =– 75<0.·

Ответ:15км/ч

Из города А в город В одновременно выехали два автомобиля. Скорость первого автомобиля – 60 км/ч, а скорость второго – 90 км/ч. Спустя 30  минут из города А в город В выехал третий автомобиль, который догнал сначала первый автомобиль, а через час после этого догнал второй автомобиль. Найдите скорость третьего автомобиля.

РЕШЕНИЕ: 

1 способ:

Пусть х км/ч – скорость третьего автомобиля, а у ч – время до встречи с первый автомобилем. Тогда (у + 0,5)ч – время первого автомобиля до встречи, а (у + 1,5)ч – время второго автомобиля до встречи.

Составим и решим систему уравнений:

БЛОК 4. Проверка приобретенных знаний, умений и навыков.

1.Диагностика или самодиагностика.

БЛОК 5. Подведение итогов, домашнее задание.

1. Рефлексия  (достигнуто или не достигнуто по образовательным результатам)

Обсуждаем итоги урока, выставляем оценки в журнал.

1.Урок был полезен.На экзамене обязательно буду решать задание №21(задачу)

2.Что было трудным?

3.Что так и осталось непонятным?

Домашнее задание. Задачи из ОГЭ на движение(задание №21)

1.Из пункта А в пункт В одновременно выехали два автомобилиста. Первый про-ехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 9 км/ч, а вторую полови-ну пути проехал со скоростью 60 км/ч, в результате чего прибыл в пункт В одно-временно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.

РЕШЕНИЕ

Пусть x (км/ч) –  скорость первого автомобилиста. Тогда скорость второго автомобилиста на первой половине пути равна (x– 9) км/ч.

Пусть весь путь это 1. Тогда t1 = 1/x –  время, которое затратил на путь первый автомобилист.

t2 = 0,5/(x-9) + 0,5/60 = 0,5/(x-9) + 1/120 –  время, которое затратил на весь путь второго  автомобилист.

Так как автомобилисты прибыли в пункт B одновременно, то составим и решим уравнение:

1/x = 0,5/(x– 9) + 1/120,

Умножим все уравнение на общий знаменатель 120x(x-9):

120 (x– 9) = 60 x + x(x– 9),

120 x –  1080 –  60x –  x2 + 9x = 0,

x2 –  69 x + 1080 = 0,

x1 = 45,

x2 = 24.

Так как по условию задачи скорость первого автомобилиста больше 40 км/ч, то

скорость первого автомобилиста равна 45 км/ч.

2.Турист проплыл на лодке по реке от пристани А до пристани В и вернулся обратно за 6 ч. Найдите скорость течения реки, если 2 км по течению реки турист проплывает за то же время, что и 1 км против течения, а расстояние между пристанями А и В  16 км.

РЕШЕНИЕ:

1 способ:

Пусть х км/ч собственная скорость лодки и у км/ч скорость течения реки, тогда (х+у) км/ч скорость по течению, (ху) км/ч скорость против течения.

Составим систему уравнений:

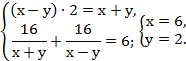
Ответ: 2км/ч

2 способ:

Пусть х км/ч скорость против течения реки, тогда 2х км/ч скорость по течению реки.

 16/2х + 16/х = 6,

8/х + 16/х = 6,

24=6х,

х= 4.

 Значит, скорость против течения реки 4км/ч.

4*2=8 км/ч – скорость по течению.

(8– 4):2= 2 км/ч – скорость течения.

Ответ: 2км/

РАБОЧИЙ ЛИСТ

Ф.И. ученика_____________________________________________________дата:________________

Тема урока___________________________________________________________________________

ЗАПИШИТЕ ФОРМУЛУ для нахождения 

Пути:                                                           Средней скорости:  

НАЧЕРТИТЕ СХЕМУ движения и укажите, как найти скорость в каждом случае

В противоположном направлении:

В одном направлении:

РЕШИТЕ ТРЕНИРОВОЧНЫЕ ЗАДАЧИ на движение (краткое решение и ответ)

Задача 1 Задача 2

Решение:                                                                      Решение:

ОТВЕТ:                                                                         ОТВЕТ:

Задача 3:

Решение:

ОТВЕТ:            

Скачано с www.znanio.ru