Разработка

Предмет: алгебра

Класс: 8

Тема урока: Определение квадратного числа

Тип урока: Урок освоения новых знаний и умений

На уроке предусмотрено использование следующих типов электронных образовательных материалов: «Диагностическая работа», «Обучающие видеоролики», «Самостоятельная работа».

Ход урока

1. Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

2. Актуализация опорных знаний.

Покажите ученикам обучающий видеоролик, напомните ранее изученный материал.

3. Осуществление учебных действий по освоению нового материала

Объясните ученикам приведённый материал и примените его к задачам.

Представьте себе, что мы решили построить дом и купили квадратный участок земли площадью 900м2. Теперь нужно огородить участок забором. Сколько метров забора потребуется поставить? Если бы мы были на месте, мы бы просто измерили периметр участка. Но эту задачу можно решить и сидя дома. Находим сторону квадрата: какое число нужно умножить на само себя, чтобы получилось 900? Разумеется, 30 Значит, нам потребуется 120 метров забора.

Ключевой момент этой задачи — найти число 30, зная его квадрат (900). Обычно, когда требовалось найти что-то неизвестное, мы к известному прибавляли число (если неизвестное было больше на сколько-то), иногда вычитали, умножали или делили. Но здесь не подойдёт ни одна из четырёх базовых операций. Здесь нам нужно найти число, которое в произведении с самим собой даёт 900 Операция эта для нас абсолютно новая, но она нередко будет появляться на практике. Дадим формальное определение.

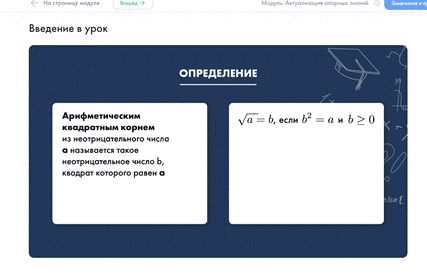
Определение. Арифметическим квадратным корнем из неотрицательного числа называют такое неотрицательное число, квадрат которого равен a.

Обозначается арифметический квадратный корень из числа так: . При этом число называют подкоренным числом (а в случае, когда под корнем находится не одно число, а сумма или, например, многочлен, говорят о подкоренном выражении).

Почему квадратный корень так называется? Дело в том, что по сути мы только что решали уравнение = a. А что значит решить уравнение? Это значит найти все числа, при подстановке которых в уравнение вместо получается верное числовое равенство. Такие числа называются корнями уравнения. Поэтому логично называть решение этого уравнения квадратным корнем из числа 900 Корнем — потому что это корень уравнения, а квадратным — потому что в уравнении мы возводим в квадрат. Кстати, в дальнейшем мы не будем каждый раз писать или говорить «арифметический квадратный корень», обычно говорят «квадратный корень» или даже просто «корень», если не возникает двусмысленности.

Но вернёмся к уравнению x2 = 900.

Несложно увидеть, что, кроме 30, подходит и число -30. Действительно, умножая -30 на -30, мы также получим 900. В то же время следует отличать: арифметический квадратный корень из числа 900 равен 30 (и только 30), а вот корни уравнения x2 = 900 — это числа 30 и -30. Когда говорят «корень из числа» — это всегда «арифметический квадратный корень». Отдельный вопрос, нет ли у этого уравнения других решений, но к этому мы вернёмся позднее.

Контрольный вопрос. Является ли число -2 корнем уравнения = 4?

Контрольный вопрос. Верно ли, что  = -2?

4. Применение знаний, в том числе в новых ситуациях.

Предложите ученикам самостоятельно решить задачи, помогите им, если возникнут трудности.

5. Домашнее задание

Предложите ученикам выполнить домашнее задание.

№127, стр.47