Разработка

                                               План урока

Тема: Гистограммы.

Учитель:

1.Класс:

2.Тип урока: Урок освоения новых знаний и умений

 3.Планируемые результаты:

Ключевы еслова: среднее арифметическое, гистограмма, случайная изменчивость, частота значения, диаграмма частот, построение графиков.

Краткое описание: Урок по предмету «Вероятность и статистика» для 7 класса по теме «Графическое представление разных видов случайной изменчивости». Урок освоения новых знаний и умений. На уроке предусмотрено использование следующих типов электронных образовательных материалов: «Диагностическая работа», «Самостоятельная работа».

                                Блочно-модульное описание урока

БЛОК1. Вхождение  в тему урока и создание условий для осознанного восприятия нового материала.

1.Мотивирование на учебную деятельность

На прошлом уроке мы познакомились с гистограммами. Когда данных много, и они почти не повторяются, обычные диаграммы непригодны. В таких случаях для наглядного представления и изучения изменчивости данных строят гистограмму – диаграмму частот. Данные группируются по величине, вычисляется частота (доля) данных в каждом интервале группировки, и уже по найденным частотам строится столбиковая диаграмма.

Подробно разберите примеры:

Пример 1.

Рост человека

Невозможно заранее предсказать рост незнакомого человека. Для исследователя эта величина случайная. Но если измерить рост многих людей (случайно выбранных), то проявится закономерность. Чтобы в этом убедиться, мы обсудим данные о росте человека по малому, среднему и большому числу наблюдений.

Малая выборка. В таблице 1 приведены результаты исследования – измерения роста двадцати случайно выбранных девушек, живущих в Москве.

В выборке размах значений равен 13: рост колеблется между 158 и 171 см. Среднее значение роста равно 165,35, медиана – 165,5.

На основе данных исследования построим гистограмму. Для этого нужно сгруппировать данные и найти частоту. Выберем шаг группировки 1 см и найдем частоту для каждого интервала значений (см. табл. 2).

Построим гистограмму – столбиковую диаграмму частот. На горизонтальной оси отмечается рост в см, на вертикальной оси – частота (рис. 1). Гистограмма имеет причудливую форму. Что будет, если увеличить объём выборки?

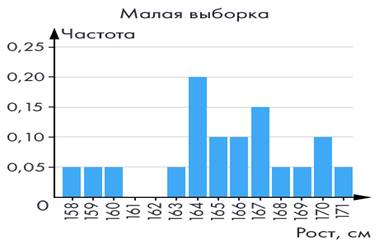
Рис. 1 Гистограмма роста (20 измерений)

Средняя выборка. Пополним наблюдения. К двадцати значениям
добавим ещё тридцать (см. таблицу 3). Среднее значение роста в этой выборке равно 165,3 см, а медиана – 165 см. Эти значения мало отличаются от тех, что были получены на малой выборке.

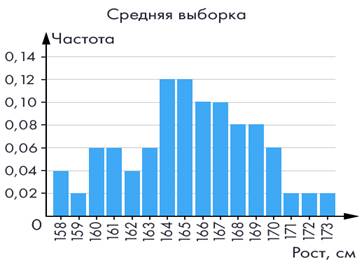
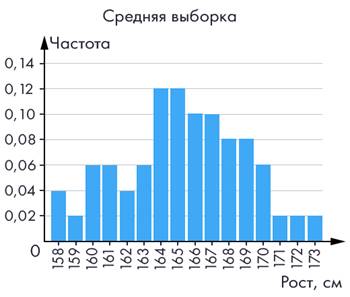
А размах вырос до 15 см. Это естественно: чем больше выборка, тем выше шансы, что в нее попадут очень высокие и очень низкие люди. Поэтому размах увеличивается, а среднее значение устойчиво. Построим новую гистограмму (рис. 2). На ней уже хорошо видно, что значения
концентрируются вблизи среднего.

Рис. 2 Гистограмма роста (50 измерений)

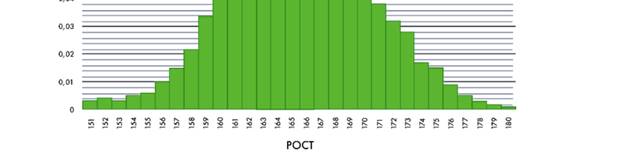
Большая выборка. Увеличим выборку до 300 человек и ещё раз построим гистограмму (рис. 3). Обратите внимание учеников на то, что её форма уже отчётливо напоминает колокол.

Большая выборка. Увеличим выборку до 300 человек и ещё раз построим гистограмму (рис. 3). Обратите внимание учеников на то, что её форма уже отчётливо напоминает колокол.

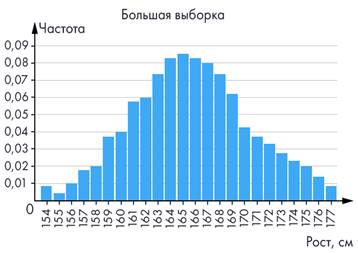
Рис. 3 Гистограмма роста (300 измерений)

Проведём плавную линию, примерно повторяющую форму гистограммы. Получится кривая, которая похожа на колокол (рис. 4). Причина проста: средние значения встречаются чаще, далекие от среднего – реже.

Зная форму гистограммы распределения, можно спрогнозировать долю девушек определённого роста, причем не в данной выборке, а, например, среди всех москвичек.

Например, рост 167 имеет частоту 0,08, что даёт основания думать, что вообще девушек ростом около 167 см в Москве примерно 8 %. Можно предположить, что доля девушек с ростом 162 – 170 см примерно 70%, а тех, чей рост превышает 170 см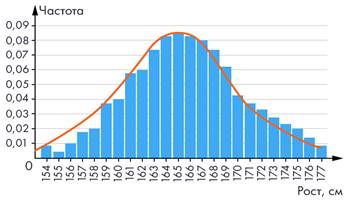 – около 15%.

Рис. 4 Колоколообразная кривая

Объяснить, почему получается именно такая форма, можно с помощью мысленного эксперимента. Представим себе, что каждая девушка заняла «своё место» на числовой прямой (рис. 5). Девушек очень малого роста (например, ниже 155 см) совсем мало. Точно так же мало очень высоких девушек (скажем, с ростом более 180 см).

Поэтому края получившейся гистограммы низкие. Большинство девушек среднего роста или около среднего роста, поэтому центральная часть гистограммы высокая.

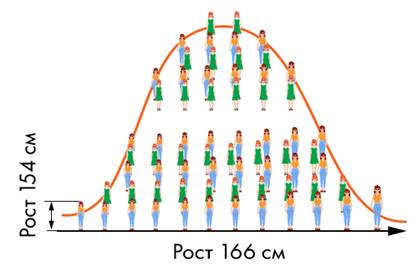
Рис. 5

Но не следует думать, что все случайные величины в природе подчиняются такому или похожему закону. Встречаются закономерности другого характера.

Пример 2. Рассмотрим длительность разговоров по мобильному телефону. Мы собрали данные о длительности всех разговоров одного абонента в течение месяца. Всего разговоров за месяц было 387. Самый короткий разговор длился всего секунду. Самый длинный — более 15 минут (924 секунды).

Интересно посмотреть на частоты разговоров разной длительности. Построим гистограмму по имеющимся данным. Нужно выбрать подходящую группировку.

Если шаг слишком малый, то интервалов очень много, и характер изменчивости плохо виден из-за «прыгающих» столбиков. Вроде бы информации много, а общую картину не видно. Мы даже не стали изображать всю получившуюся гистограмму — она слишком длинная. Получившаяся диаграмма (см. рис. 6) неудачная: слишком мал шаг группировки.

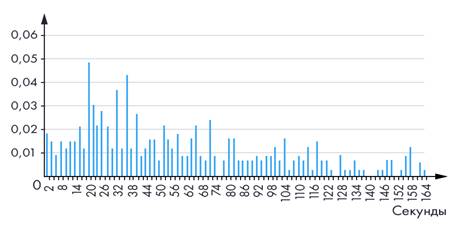
Рис. 6

Если шаг слишком большой, то интервалов мало, и картинка получается очень грубая — слишком много полезной информации теряется. Получившаяся диаграмма (см. рис. 7) малоинформативна из-за слишком большого шага.

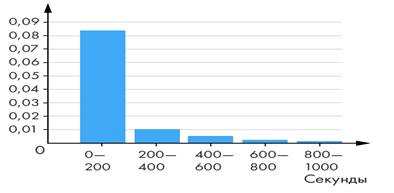
Рис. 7

Шаг группировки нужно выбрать так, чтобы, с одной стороны, диаграмма была достаточно подробной, а с другой — отражала бы общую тенденцию и хорошо показывала характер случайной изменчивости данных. При шаге 25 секунд (для простоты на оси абсцисс отмечены только правые концы интервалов) гистограмма достаточно подробная, и хорошо видна убывающая тенденция — чем длительнее разговоры, тем таких разговоров меньше (см. рис. 8).

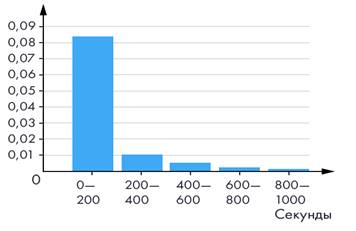
Рис. 8

Гистограмма имеет совершенно другую форму по сравнению с гистограммой частот роста девушек. Это означает, что и характер изменчивости совсем другой.

2. Актуализация опорных знаний

(формы организации учебной деятельности: индивидуальный, групповой, работа в паре).

Задание№1……..

3. Целеполагание

(Назовите цель: ты узнаешь, ты научишься……)

БЛОК 2. Освоение нового материала

1.Осуществление учебных действий по освоению нового материала

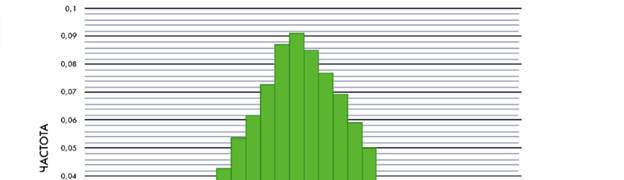
На гистограмме данные исследования продолжительности службы (в годах) электрического чайника одной конкретной модели.

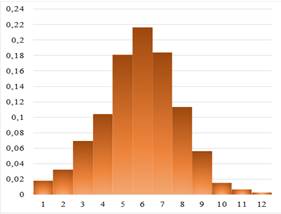
1. Оцените приблизительно по гистограмме среднее время работы чайника.

2. Производитель определил гарантийный срок 4 года. Оцените, какая доля проданных чайников выходит из строя в течение гарантийного срока.

3. Каким должен быть гарантийный срок, чтобы в течение гарантийного срока из строя выходило не более 10% проданных чайников?

2.Проверка первичного закрепления

(Сформулируйте…Изложите факты…..Проверьте себя….Дайте определение понятию….(Установите, что….(где,когда).Сформулируйте главное…(правило,закон,мысль)

Задание №1……..(на выполнение дается 5 мин.)

БЛОК 3.  Применение изученного  материала

1.Применение знаний,  в том числе в новых ситуациях

Юный статистик проводит серию экспериментов. В первый день он кидал игральный кубик до тех пор, пока не выпала «шестёрка». В таблицу он заносил данные о том, с какого броска это произошло. Так он делал много раз. Во второй день он делал то же самое, но до тех пор, пока не выпадет «тройка».

Каждый день он делал ровно 200 измерений. На рисунке 6 представлены гистограммы за два дня. По горизонтали отмечено число бросков кубика, в результате которых выпало нужное число, а по вертикали – частота этого события. Сравните гистограммы за 1-й и 2-й день. Можно ли предположить, что изменчивость данных подчиняется одинаковой закономерности?

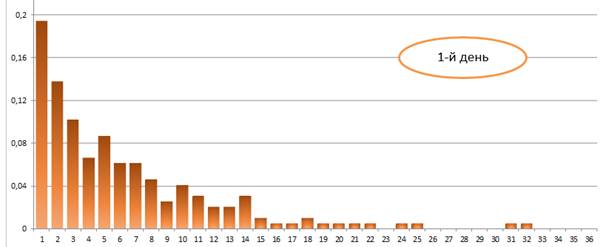
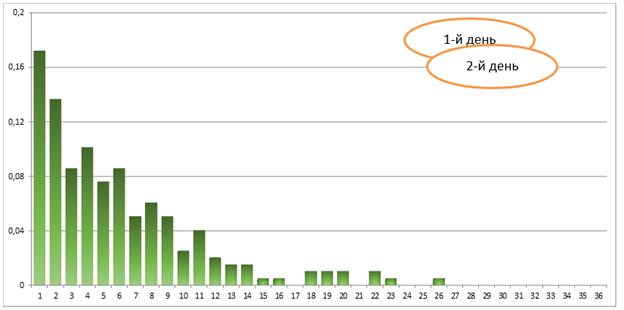
1.     2.Выполнение межпредметных заданий из реальной жизни.

3.Задание ЕГЭ и ОГЭ

На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.

Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.

Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответ нужно записать число 51118).

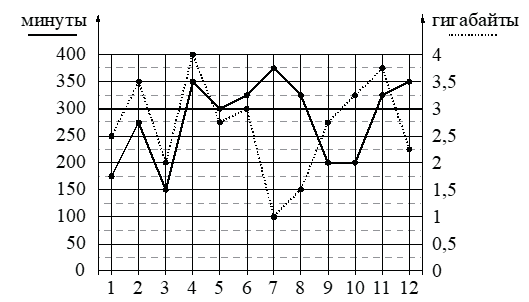
4.Развитие ФГ

Подбор соответствующего задания.

5.Систематизация знаний и умений

(Подбираем задания на связь изученной на уроке темы  с раннее освоенной темой или другими  предметами)

БЛОК 4. Проверка приобретенных знаний, умений и навыков.

1.Диагностика или самодиагностика.

Самостоятельная работа(указываем в какой форме, озвучиваем критерии оценивания ….

 (Если 5 заданий выполнено правильно, то будет «5» и т.д….)

БЛОК 5. Подведение итогов, домашнее задание.

1. Рефлексия  (достигнуто или не достигнуто по образовательным результатам)

Обсуждаем итоги урока, выставляем оценки в журнал.

1.Что на уроке больше всего понравилось (запомнилось)?

2.Что было трудным?

3.Что так и осталось непонятным?

2. Домашнее задание.

Рекомендации по ДЗ.