Поделиться
-«Четные и нечетные функции».docx
План урока
Учитель:
Класс 10(базовый уровень)
Тема: «Четные и нечетные функции»
Тип урока:урок повторения
Планируемые результаты:выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа;
Личностныеумение ставить перед собой цель, видеть ожидаемый результат работы; умение рационально распределять рабочее время;
Предметные:вспомнить ранее изученные свойства функции;познакомиться с чётными и нечётными функциями и их графиками;выработать умение строить графики чётных и нечётных функций и определять по графику вид функции
Метапредметныеумение объективно оценивать свои возможности, анализировать свои результаты, корректировать свои действия;
владение навыками познавательной рефлексии;
Ключевыеслова:«четная функция», «нечетная функция», «периодические функции», «монотонность функции»;
Краткое описание:
Оборудование и материалы: презентация
Блочно-модульное описание урока
БЛОК1. Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
1.Мотивирование на учебную деятельности
- Здравствуйте, ребята! Садитесь! В предыдущем параграфе мы обсуждали те свойства функций, которые в той или иной степени были нам знакомы.
Ребята, какие свойства функции вы знаете?
(Д(у), Е(у), монотонность, ограниченность сверху, снизу, Выпуклость вверх, вниз
2.Актуализация опорных знаний
(формы организации учебной деятельности: индивидуальный, групповой, работа в паре)
Тестирование.
|
I вариант |
II вариант |
|
|
1. Область определения y=x2-3x+9 2.Область
определения у=
|
1. Область
определения у=
2. Область
определения у=
|
|
|
a) (-∞;-1)U(-1;1)U(1;+∞); б) (- ∞;0)U (0;+ ∞); в) [-10; +∞); г) (-1;1); д) (-∞;+∞) е) (-∞;5) U (5;+ ∞); ж) (3;+ ∞) |
||
|
3) На рисунке дан график функции у=f(x). Данная функция: а) выпукла вверх; б) выпукла вниз; в) не выпукла. |
3) На рисунке дан график функции у=f(x). Данная функция: а) выпукла вверх; б) выпукла вниз; в) не выпукла. |
|
|
4) На рисунке дан график функции у=f(x). Определите для данной функции унаим: а) 0; б) 3; в)4; г)-3
|
4) На рисунке дан график функции у=f(x). Определите для данной функции унаиб: а) 0; б) 5; в)4; г)-3 |
|
|
5) На рисунке дан график функции у=f(x). Определите для данной функции унаиб: а) 0; б) 3; в)4; г)-3 |
5) На рисунке дан график функции у=f(x). Определите для данной функции унаим:а) а) 0; б) 3; в)4; г)-3
|
|
3. Целеполагание
Слайд1. Китайская пословица гласит:
"Я слушаю, - я забываю;
Я вижу, - я запоминаю;
Я делаю, - я усваиваю"
Что же мы должны сегодня услышать, увидеть и сделать? Посмотрим на тему урока.
СЛАЙД№2
Сегодня мы продолжаем разговор о свойствах числовых функций. Речь пойдёт о чётных и нечётных функциях.
Запишите, пожалуйста, в тетрадях число и тему урока: “Чётные и нечётные функции”.
Цель нашего урока усвоить определение чётной и нечётной функции и их основные свойства, научиться определять- четная функция или нет, научиться строить графики таких функций и применять эти знания к решению задач.
БЛОК 2. Освоение нового материала
1.Осуществление учебных действий по освоению нового материала (формы организации учебной деятельности,включая самостоятельную деятельность учащихся (изучаем новое,открываем новое).
СЛАЙД №3
ЗАДАНИЕ Функция задана формулой f(x)= х2. Найти: а) D(f); б) f(2), f(-2), f(-x).
Что вы увидели? (f(-x)=f(x)). Дана функция, знак которой не меняется при изменении знака x.
Для данной функции выполняется два условия: 1) f(-x)=f(x); 2) D(f) симметрична относительно нуля.
Такая функция называется четной.
СЛАЙД №4 (определение четной функции). Запишите определение.
Приведите примеры ч.ф.: y = x2y = –x2y = x4y = x6y = x8 +2 x2
Четные функции обладают важным свойством: График четной функции симметричен относительно оси ординат. СЛАЙД №5 (графики ч.ф.)
СЛАЙД №6
ЗАДАНИЕ Функция задана формулой f(x)= х3
Найти: а) D(f); б) f(1), f(-1), f(-x).
Что вы увидели? (f(-x)= -f(x)). Дана функция, знак которой меняется при изменении знака x.
Для любого ли х значение –х также принадлежит области определения? Т.е. D(f) симметрична относительно нуля? (да)
Такая функция называется нечетной
СЛАЙД №7 (определение нечетной функции). Запишите определение.
Примеры неч.ф.: y = x3 y = –x3 у = х5 у = х7 у = х3+х9 у=х(5-х2)
Нечетные функции обладают важным свойством: График нечетной функции симметричен относительно нач. координат. СЛАЙД №8, №9 (графики неч.ф.)
Задание. Функция задана формулой функция
у = 2х + 3. Сравните значения функции при х=-1 и х=1. В самом деле, f(1) = 5, а
f (-1) = 1. Как видите, здесь 
Значит,
не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность
примеры.
Опр. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем,
(-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как [0, +оо), (-2, 3),
[-5, 5) — несимметричные множества. Если функция у = f (х) — четная или нечетная, то ее область определения D (f) — симметричное множество. Если же D (f) — несимметричное множество, то функция у = f(х) не является ни четной, ни нечетной.
2.Проверка первичного закрепления
1)Укажите номера графиков:
а) четных функций; б) нечетных функций; в) функций, не являющихся ни четными, ни нечетными
|
1). |
|
6). |
|
|
2). |
|
7). |
|
|
3). |
|
8). |
|
|
4). |
|
9). |
|
|
5). |
|
10). |
|
2. Функция y=f(x) четная. Дан фрагмент графика. Найти f(–3)
1)–5 2)0 3)5 4)–1
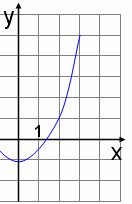3. Функция y=f(x)
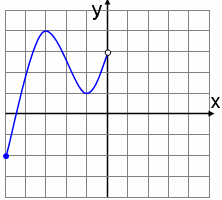
нечетная. Дан фрагмент графика. Найти f(3)
1 )–4 2)4 3)3 4)–3
4.Найдите значение выражения f(3) + f(-5), если известно, что у=f(x) – четная функция и f(-3)=2, f(5)=-3.
5. Найдите значение выражения f(7) – f(-2), если известно, что у=f(x) – четная функция и f(-7)=0,3, f(2)= - 0,4
6. Найдите значение выражения f(4) – f(-5), если известно, что у=f(x) – нечетная функция и f(-4)=2,5, f(5)= 1,3.
БЛОК 3. Применение изученного материала
1.Применение знаний, в том числе в новых ситуациях
Ответить на вопросы:
1) Может ли быть четной или нечетной функция, областью определения которой является:
а)
промежуток 
; б)
промежуток 
; в)
объединение промежутков 
.
2) Функция 
четная, 
. Найти 
.
3) Функция 
четная, 
. Найти 
.
2.Выполнение межпредметных заданий из реальной жизни.
3.Задание ЕГЭ и ОГЭ
4.Развитие ФГ
Подбор соответствующего задания.
5.Систематизация знаний и умений
(Подбираем задания на связь изученной на уроке темы с раннее освоенной темой или другими предметами)
БЛОК 4. Проверка приобретенных знаний, умений и навыков.
1.Диагностика или самодиагностика.
Исследовать на четность функции:
а) 
б)
в) 
БЛОК 5. Подведение итогов, домашнее задание.
А теперь подведем итоги урока. Заполните пропуски в формулировке определений и свойств. СЛАЙД № 20,21,22
1.Рефлексия (достигнуто или не достигнуто по образовательным результатам)
Обсуждаем итоги урока, выставляем оценки в журнал.
1.Что на уроке больше всего понравилось (запомнилось)?
2.Что было трудным?
3.Что так и осталось непонятным?
2. Домашнее задание.
Рекомендации по ДЗ. Решу ЕГЭ.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
