Разработка 6

Тема урока: « Сравнение целых чисел»

Цель урока: формирование  навыка сравнения отрицательных чисел и чисел с разными знаками.

Задачи урока: сформировать  навыки сравнения чисел с разными знаками.

Планируемые результаты:

Предметные: Знать: правила сравнения, сложения отрицательных чисел, сложения чисел с разными знаками, вычитания рациональных чисел.

Метапредметные: Коммуникативные: слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения.

Регуляционные: проводить контроль в форме сравнения способа действия и его результат с заданным эталоном с целью обнаружения отклонений от эталона и внесения необходимых коррективов.

Познавательные: выделять существенную информацию из текстов разных видов.

Личностные: Формирование стартовой мотивации к изучению нового

Техническое обеспечение урока: компьютер

Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы): рабочая тетрадь 6 класс М.К. Потапов, А.В. Шевкин. тесты 6 класс С.Г. Журавлев, В.В. Ермаков, Ю.В. Перепелкина, В.А. Свентковский.

Содержание урока:

I.                   Организационный момент.

II.                Актуализация опорных знаний.

1.      Устный счет

1)      êх ê= 2;      2)  êх ê= 25;    3) êх ê= -13.

2)      В мастерской по пошиву одежды от куска сукна в 200 м ежедневно. Начиная с 1 марта, отрезали по 20 м. Когда был отрезан последний кусок?  (9 марта).

3)      Сравните натуральные числа: 1 * 10;  25 * 7;   99 * 100.

4)      Сравните обыкновенные дроби с одинаковыми знаменателями:                                  1)             и  ;        2)     2  и  2;      3)      и 1.

III.             Индивидуальная работа по карточкам.

Карточка 1.

1.      Запишите: а) положительные числа, модули которых равны 7, 15, 0,  .

б) отрицательные числа, модули которых равны 1, 34, 2 .

                  2. Выполните действия: а) ê+6 ê+ ê-3 ê;  б) ê-5 ê- ê+2 ê;    в) ê-12 ê+ ê+8 ê.

                  Карточка 2.

1.       Запишите: а) положительные числа, модули которых равны 17, 5, 0, 3 .

б) отрицательные числа, модули которых равны 21, 4,  .

                  2. Выполните действия: а) ê+14 ê+ ê-5 ê;  б) ê-23 ê- ê+2 ê;    в) ê-25 ê+ ê+18 ê.

IV.             Изучение темы урока.

Ребята, вы умеете сравнивать любые положительные числа друг с другом и с нулём. А как вы думаете, отрицательные числа можно сравнивать? Конечно! И отрицательные друг с другом, и отрицательные с положительными, и отрицательные с нулём. Сегодня на уроке мы об этом и поговорим.

Нначертим координатную прямую, отметим на ней начало отсчёта, выберем единичный отрезок и укажем направление.

Напомним, на горизонтальной координатной прямой положительные числа изображаются правее нуля,

  а отрицательные – левее нуля. Возьмём два числа, например, 1 и3 . Вы знаете, что 1 < 3 . Отметим на координатной прямой точки А(1) и В(3 ).

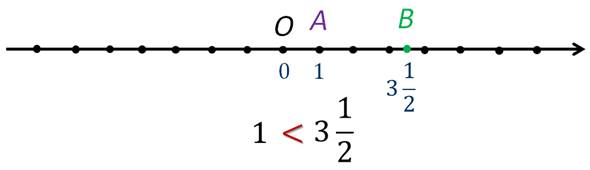
Понятно, что точка А на координатной прямой расположена левее точки В.

Напомним, правило: на горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой. Соответственно, на горизонтальной координатной прямой точка с меньшей координатой лежит левее точки с большей координатой.

А теперь давайте возьмём два отрицательных числа, например, ­­– 2 и – 4 . Как сравнить такие числа? Отметим на координатной прямой точки С(– 2) и D(– 4  ).

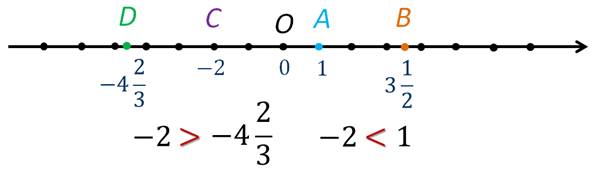
Запишем правило сравнения любых чисел:

Из двух чисел больше то, которое изображается на горизонтальной координатной прямой правее. И, соответственно, из двух чисел меньше то, которое  изображается на горизонтальной координатной прямой левее.

Пример

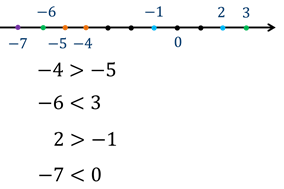
Хотелось бы сразу уточнить, что все положительные числа больше нуля, а все отрицательные – меньше нуля.

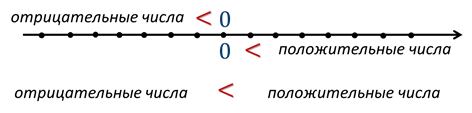
 Любое отрицательное число меньше положительного.

Вообще очень удобно сравнивать числа при помощи понятия «модуль числа». Так как большее из двух положительных чисел на координатной прямой изображается правее, т.е. дальше от начала отсчёта, то это число имеет больший модуль.

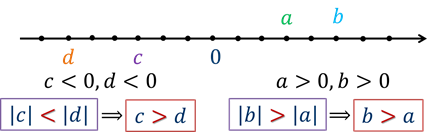
Запомните, из двух положительных чисел больше то, чей модуль больше.

Так как большее из двух отрицательных чисел на координатной прямой изображается правее, т.е. ближе к началу отсчёта, то это число имеет меньший модуль.

Запомните, из двух отрицательных чисел больше то, чей модуль меньше.

Итак: Из двух чисел больше то, которое изображается на горизонтальной координатной прямой правее. И, соответственно, из двух чисел меньше то, которое  изображается на горизонтальной координатной прямой левее.

Все положительные числа больше нуля.

Все отрицательные – меньше нуля.

Любое отрицательное число меньше положительного.

Из двух положительных чисел больше то, чей модуль больше.

Из двух отрицательных чисел больше то, чей модуль меньше.

V.                Закрепление темы урока.

1.      Работа по учебнику

1)      Выполнить устно № 232 – 237.

2.      Работа по рабочей тетради

Выполнить № 93 – 95

3.      Выполнить тест 11.

VI.             Итоги урока. Рефлексия.

Над какой темой работали на уроке?

Как вы оцениваете свою работу?

Сформулируйте правила сравнения целых чисел.

VII.          Домашнее задание: прочитать п. 2.3  № 238 – 240.