Разработка к уроку

Предмет: Геометрия                                                                            

Класс: 10                                        

 Параллельность прямых и плоскостей в пространстве. Параллельность прямой и плоскости

https://resh.edu.ru/subject/lesson/6065/start/125652/

Цели:

·         получить знания о параллельности прямых и плоскостей;

Задачи:

·         рассмотреть возможные случаи взаимного расположения прямых и плоскостей в пространстве;

·         познакомиться с понятиями параллельных и скрещивающихся прямых и их основными свойствами;

·         доказать теорему о параллельных прямых в пространстве и параллельности трех прямых.

На уроке

мы узнаем:

·         о взаимном расположении прямых в пространстве; о взаимном расположении прямой и плоскости; о скрещивающихся прямых;

мы научимся:

·         доказывать теорему о параллельных прямых в пространстве и параллельности трех прямых; доказывать признаки параллельности прямой и плоскости;

мы сможем:

·         применять доказанные теоремы при решении задач.

Тип урока:

На уроке предусмотрено использование следующих электронных образовательных материалов:

Ключевые слова

Перечень вопросов, рассматриваемых в теме

1. Определение параллельных прямых;
2. Теорема о единственности прямой, параллельной данной, проходящей через данную точку;
3. лемма о двух параллельных прямых;
4. теорему о параллельности трех прямых;
5. определение параллельных прямой и плоскости;
6. признаком параллельности прямой и плоскости.

Глоссарий по теме

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Ход урока:

1.      Вхождение в тему урока и создание условий для осознанного восприятия нового материала:

Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого учёного Евклида (III век до нашей эры), создавшего руководство по математике под названием «Начала». В этой книге есть раздел о параллельных прямых. Что же такое параллельные прямые в пространстве, и сильно ли они отличаются от параллельных прямых на плоскости?

2.      Освоение нового материала:

1)      Осуществление учебных действий по освоению нового материала

https://resh.edu.ru/subject/lesson/6065/main/125655/ ( видео)

В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».

В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».

В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.

В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.

Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).

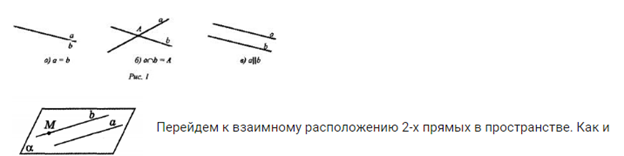
в планиметрии, две различные прямые в пространстве либо пересекаются в одной точке, либо не пересекаются (не имеют общих точек). Но второй случай допускает две возможности: прямые лежат в одной плоскости (параллельны) или прямые не лежат в одной плоскости. В первом случае они параллельны, а во втором - такие прямые называются скрещивающимися.

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

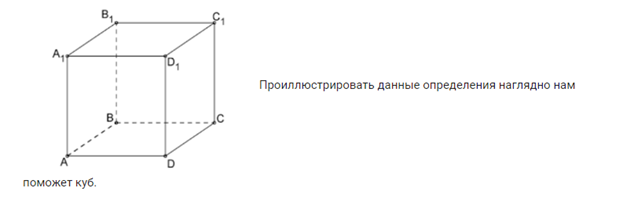
Давайте укажем некоторые пары параллельных прямых:

AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.

А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:

AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.

Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

1. М и а задают плоскость α
2. Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. в плоскости α.
3. В плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна- это нам известно из курса планиметрии.
4. На чертеже эта прямая обозначена буквой b .
5. Следовательно, b-единственная прямая, проходящая через точку М параллельно прямой а.

Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.

Аналогично определяется параллельность отрезка и прямой, а так же параллельность двух лучей.

1. Рассмотрим две параллельные прямые a и b и допустим, что прямая b пересекает плоскость α в точке M(а рис.).
2. Мы знаем, что через параллельные прямые a и b можно провести только одну плоскость β. (теорема)

1. Так как точка M находится на прямой b, то M также принадлежит плоскости β (б рис.). Если у плоскостей α и β есть общая точка M, то у этих плоскостей есть общая прямая p, которая является прямой пересечения этих плоскостей (4 аксиома).

1. Прямые a, b и c находятся в плоскости β.

Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.

1. Точку пересечения прямых a и p обозначим за N.

Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.

1. Значит, прямая a пересекает плоскость α в точке N.

Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Дано: a∥c и b∥c

Доказать: a∥b

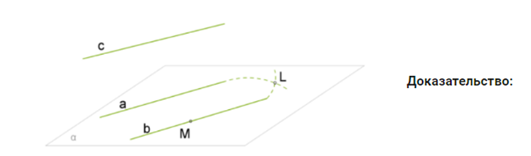
Выберем точку M на прямой b.

Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).

Возможны два случая:

1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.

Пусть прямая b пересекает плоскость α.

Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α. 

Теперь нужно доказать, что прямые a и b параллельны.

Пусть у прямых a и b есть общая точка L.

Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.

Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.

Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Обозначение: a||α.

Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.

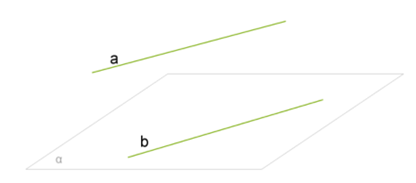
Существует еще два утверждения, которые используются при решении задач:

1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.

3.       Применение изученного материала:

1)      Применение знаний, в том числе в новых ситуациях

Обсудите с учащимися предложенные примеры и задачи.

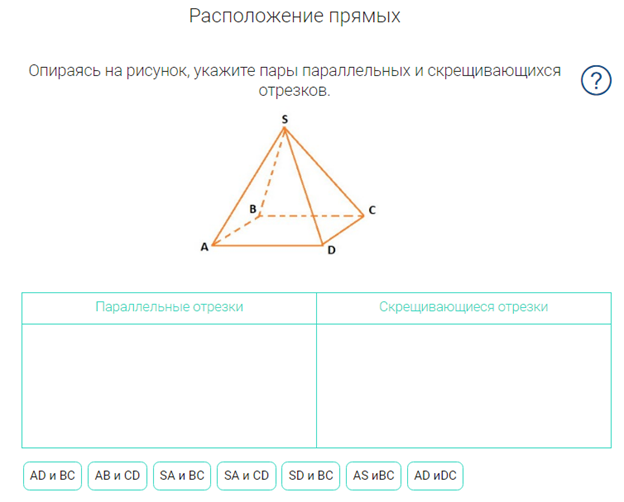
Примеры и разбор решения заданий тренировочного модуля

№2

Тип задания: Ввод с клавиатуры пропущенных элементов в тексте

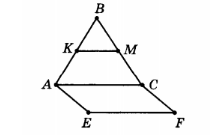
А)Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.

Найти: EF

Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10

Т.к. ACFE − параллелограмм, то АС=EF=10

Ответ: EF=10

Б) Подчеркните пары параллельных прямых

1. КМ и АС

2. АС и ЕF

3. KM и EF

4. AE и CF

5. AE и EF

6. КМ и CF

№3.

Тип задания: Единичный / множественный выбор

Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.

·          

1.      АВ=2 см

2.      АВ=4 см

3.      АВ=5 см

4.      АВ=10 см

Решение:

2)      Выполнение заданий в формате ГИА(ОГЭ,ЕГЭ)

Предложите учащимся решить задачу самостоятельно. Расскажите учащимся решение этой задачи.

4.      Подведение итогов, домашнее задание:

Подведение итогов

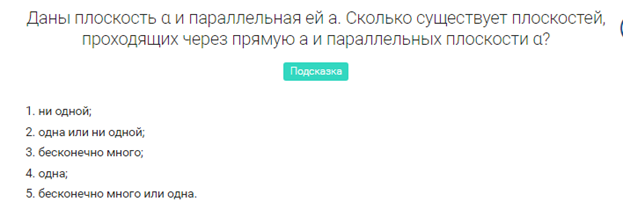
Предложите учащимся задачи для самостоятельного решения дома.

Скачано с www.znanio.ru