
План урока
Класс: 10б
Тема: Решение целых и дробно-рациональных уравнений и неравенств
Библиотека ЦОК:урок №163(8 кл), урок №234(9кл)
Тип урока: урок закрепление
Планируемые результаты: Формирование у учащихся навыков решения дробно-рациональных уравнений. Формирование и развитие у учащихся пространственного воображения
Личностные:воспитывать чувство сплоченности, взаимопомощи, воспитывать умения работать индивидуально над задачей
Предметные:формирование умений и навыков решения дробно-рациональных уравнений и неравенств
Метапредметные:развитие графической культуры и математической речи
Ключевыеслова:корень уравнения, рациональные выражения, модель
Базовые понятия, единые для школьного образования:алгоритм, равенство, объект
Краткое описание:урок №163 (8 класс)На уроке предусмотрено использование следующих типов электронных образовательных материалов: «Диагностическая работа», «Самостоятельная работа».
Блочно-модульное описание урока
БЛОК1. Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
1.Мотивирование на учебную деятельностиЗдравствуйте, ребята! На доске написаны
уравнения посмотрите на них внимательно. Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений и неравенств».
2.Актуализация опорных знаний (Вопросы )
3. ЦелеполаганиеТема нашего урока «Решение целых и дробно-рациональных уравнений и неравенств». Как вы думаете какая цель нашего урока?
БЛОК 1. Освоение нового материала
1.Осуществление учебных действий по освоению нового материала
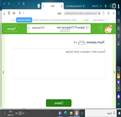
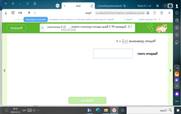
Объяснить ученикам приведённый материал и применить его к задачам. Мы изучали рациональные выражения, а теперь будем решать уравнения с ними. Уравнения, в обеих частях которых стоят рациональные выражения, называются рациональными. В случае, когда в рациональном уравнении есть деление на выражение с переменной, уравнение называется дробно-рациональным.Для начала научимся решать дробно-рациональные уравнения, которые содержат всего однурациональную дробь и имеют вид �(�)�(�)=0, где f(x) и g(x) — многочлены первойили второй степени.
Вы уже знаете, что числовая дробь mfracmfrac равна 0 тогда и только тогда, когда её числитель равен 0, а знаменатель отличен от 0:
a = 0 ,b ≠ 0.Это верно и для рациональной дроби: �(�)�(�)=0 тогда и только тогда, когдаf(x) = 0,g(x) ≠ 0.Таким образом, для того чтобы решить уравнение �(�)�(�)=0, мы должны приравнять к 0 егочислитель (f(x) = 0), найти решения этого уравнения и отобрать те из них, при которых g(x ≠ 0.
Алгоритм решения дробных рациональных уравнений:
1) найти наименьший общий знаменатель дробей, входящих в уравнение, при необходимости прежде разложить знаменатели дробей на множители;
2) умножить обе части уравнения на наименьший общий знаменатель;
3)решить получившееся целое уравнение;
4) исключить из его корней те, которые обращают в нуль общий знаменатель.
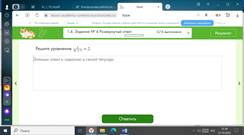
2.Проверка первичного закрепления
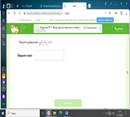
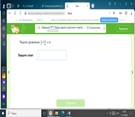
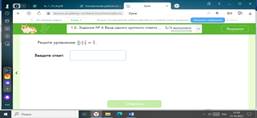
БЛОК 3. Применение изученного материала
1.Применение знаний, в том числе в новых ситуациях
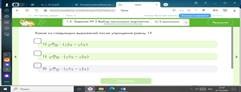
Самостоятельная работаПредложить ученикам самостоятельно решить задачи на развитие функциональной грамотности, помогите им, если возникнут трудности.
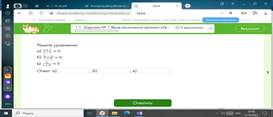
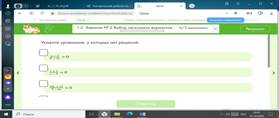
2. Выполнение задание из ЕГЭ
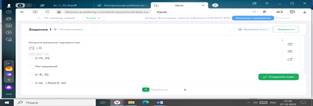
БЛОК 4. Проверка приобретенных знаний, умений и навыков.
1.Диагностика или самодиагностика.
Самостоятельная работа(указываем в какой форме, озвучиваем критерии оценивания ….
(Если 5 заданий выполнено правильно, то будет «5» и т.д….)
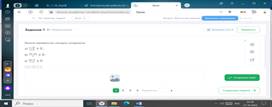
БЛОК 5. Подведение итогов, домашнее задание.
1.Рефлексия (достигнуто или не достигнуто по образовательным результатам)
2. Домашнее задание:предложить ученикам выполнить домашнее
задание.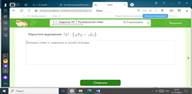
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.