Разработка урока

 План урока

Учитель:

1.Класс :8

2.Тип урока:  урок освоения новых знаний

3.Тема урока: Формулы для площади треугольника, параллелограмма

4.Планируемые результаты:

Личностные: математической направленности, осознанием важности математического образования на всю жизнь для успешной профессиональной деятельности и развития необходимых умений, осознанным выбором и построением индивидуальной траектории образования и жизненных планов с учетом личных интересов и общественного мнения;

Предметные: выработать навык применения  формулы площади треугольника через практические задания;

Метапредметные:выбрать способ решения учебной задачи (сравнивать несколько вариантов решений, выбирать наиболее подходящие варианты с учетом, самостоятельно выделенных).

Ключевые слова:площадь чевиана треугольника

Краткое описание: Урок по предмету «Геометрия» для 8 класса по теме «Отношение площадей треугольников с общим основанием или общей высотой». Урок освоения новых знаний и умений. На уроке предусмотрено использование следующих типов электронных образовательных материалов: «Галерея изображений (группа изображений по одной тематике)», «Самостоятельная работа».

Блочно-модульное описание урока

БЛОК1. Вхождение  в тему урока и создание условий для осознанного восприятия нового материала.

1.Мотивирование на учебную деятельность

«Любой, кто перестает учиться, стар, будь то двадцать или восемьдесят лет. Тот, кто продолжает учиться, остается молодым. Самое великое в жизни — сохранять свой ум молодым».

2.Актуализация опорных знаний

Вспомнить понятие медиана треугольника, биссектриса и высота треугольника

3. Целеполагание

выработать навык применения  формулы площади треугольника через практические задания;

БЛОК 2. Освоение нового материала

1.Осуществление учебных действий по освоению нового материала

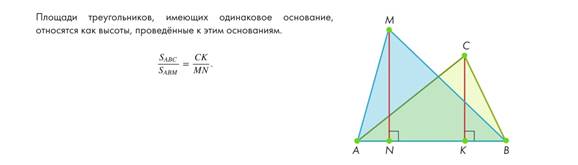
Чевианой треугольника называют отрезок, соединяющий вершину с точкой, лежащей на противоположной стороне. Примерами чевиан являются медианы, высоты и биссектрисы треугольника. Также легко показать, что треугольники с двумя равными высотами или с двумя равными медианами является равнобедренным.

Свойство чевианы треугольника

Чевиана делит площадь треугольника и его сторону в одинаковом отношении.

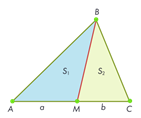
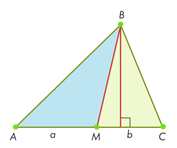
2.Проверка первичного закрепления

Задание №1

На стороне AC треугольника ABC отмечена точка D так, что AD = 3, DC = 7. Площадь треугольника ABC равна 20.

Найдите площадь треугольника BCD.

Решение:

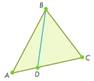
БЛОК 3.  Применение изученного  материала

1.Применение знаний,  в том числе в новых ситуациях

Задача №2

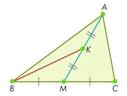Точка K — середина медианы AM треугольника ABC. Площадь треугольника BMK равна 12. Найдите площадь треугольника ABC.

Решение: Так как BK — медиана треугольника ABM, то площади треугольников ABK и MBK равны. Следовательно, площадь треугольника BMK равна 12, а площадь треугольника ABM равна 24, как сумма площадей двух его частей.

Так как АМ – медиана треугольника АВС, то S_ABM = S_ACM. Следовательно, S_AMC = 24. Тогда площадь всего треугольника S_ABC = S_ABM + S_AMC = 24 + 24 = 48

Ответ: 48

2.Выполнение межпредметных заданий из реальной жизни.

3.Задание ЕГЭ и ОГЭ

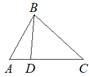
Задание№3

На стороне AD треугольника ABD отмечена точка D так, что AD=3, DC=10. Площадь треугольника ABC равна 39. Найдите площадь треугольника ABD.

4.Развитие ФГ

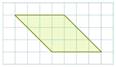
Задание№4

На клетчатой бумаге с размером клетки 1 × 1 изображён параллелограмм. Найдите его площадь

5.Систематизация знаний и умений

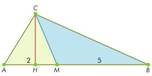
Задача №5

Точка M делит сторону AB треугольника ABC в отношении 2 : 5. В каком отношении отрезок CM делит площадь треугольника ABC?

Решение:

Пусть CH — высота треугольника ABC. Тогда треугольники ACM и BCM имеют общую высоту, проведённую из вершины C. Следовательно, по свойству площадей треугольников с общей высотой отношение их площадей равно отношению оснований, в которым у них проведена общая высота.

S_AСM : S_ВСM = AM : MB = 2 : 5

БЛОК 4. Проверка приобретенных знаний, умений и навыков.

1.Диагностика или самодиагностика.

Самостоятельная работа.

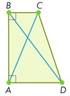
Задача №1

В прямоугольной трапеции АВСD c прямыми углами A и B проведены диагонали АС и ВD. Основания трапеции АD = 8 см, ВС = 4 см. Найдите отношение площадей треугольников АВС и АВD.

Решение:

БЛОК 5. Подведение итогов, домашнее задание.

1. Рефлексия  (достигнуто или не достигнуто по образовательным результатам)

Обсуждаем итоги урока, выставляем оценки в журнал.

1.Что на уроке больше всего понравилось (запомнилось)?

2.Что было трудным?

3.Что так и осталось непонятным?

2. Домашнее задание.

Рекомендации по ДЗ.