Поделиться
19.Тригонометрические функции острого угла в прямоугольном треугольнике. Теорема Пифагора. 2.docx
Краткосрочный план урока по Геометрии
|
Раздел долгосрочного плана: Соотношения между сторонами и углами прямоугольного треугольника |
Школа: КГУ "Гимназия № 25 им.И Есенберлина |
|
|
Дата: 14.11.2021 |
ФИО учителя: Эргашова Арофат Шухратовна |
|
|
Класс: 8 «А,Б,В» |
Количество присутствующих: отсутствующих: |
|
|
Тема урока |
Тригонометрические функции острого угла в прямоугольном треугольнике. Теорема Пифагора. 2 |
|
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) |
8.1.3.2 знать определения синуса, косинуса, тангенса и котангенса углов через отношения сторон в прямоугольном треугольнике; 8.1.3.3 доказывать и применять теорему Пифагора; |
|
|
Цели урока |
Ты узнаешь: тройки натуральных чисел, для которых выполняется теорема Пифагора. Ты научишься: применять пифагоровы тройки при решении задач. |
|
|
Ход урока
|
||
|
Этап урока/ Время |
Действия педагога |
Действия ученика |
Оценивание |
Ресурсы |
|
Начало урока Организационный момент. |
Проверить домашнее задание:
|
Совместно с учащимися определить тему и цели урока, "зону ближайшего развития". |
|
Презентация |
|
Середина урока Актуализация опорных знаний. |
|
Решить задачи индивидуально, сдать на проверку учителю. |
Взаимопроверка |
Приложение 1 |
|
Групповая работа. |
Решение задач. Объединить учащихся в однородные малые группы, согласно выбранному уровню. Подготовьте импровизированный «Сундучок» в виде коробки и.т.п. Наполните его карточками, содержащими задачи на применение теоремы Пифагора. Проверяется умение правильно начертить чертеж, использовать ранее изученные знания. Предложите каждой группе учащихся «Сундучок с заданиями». Учащиеся по очереди вытаскивают из сундучка задание и решают его. |
Ученики самостоятельно в группе распределяют задачи. Группа, решившая наибольшее количество задач и набравшая в тоже время наибольший балл, считается победителем. |
Каждая задача с практическим содержанием оценивается в 2 раза выше. |
Приложение 2 |
|
Конец урока Беседа. Рефлексия. |
Подводит итоги урока. Выставление ФО |
Задают вопросы |
«Рефлексивный ринг» |
Презентация |
|
Домашнее задание. |
|
|
|
Знать теорему Пифагора, изучить ее доказательство, решить из уровня В учебного пособия "Геометрия 8" №2.8 №2.9, №2.10 ,№2.16 |
Пифагорова тройка
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пифагорова тройка
Тройка натуральных чисел, для которых выполняется теорема Пифагора, называется пифагоровой тройкой.
⠀
Пифагорова тройка чисел называется простейшей, если ее числа взаимно простые.
Примеры часто используемых простейших пифагоровых троек:
(3; 4; 5), (5; 12; 13), (7; 24; 25), (8; 15; 17), (9; 40; 41), (20; 21; 29), (12; 35; 37), (11; 60; 61).
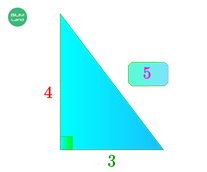
⠀ 32 + 42 = 9 + 16
32 + 42 = 25
32 + 42 = 52
То есть числа
3, 4 и 5
образуют пифагорову тройку.
52 + 122 = 25 + 144
52 + 122 = 625
52 + 122 = 252
То есть числа
3, 4 и 5
образуют пифагорову тройку.
72 + 242 = 49 + 526
72 + 242 = 625
72 + 242 = 252
То есть числа
7, 24 и 25
образуют пифагорову тройку.
82 + 152 = 64 + 225
82 + 152 = 289
82 + 152 = 172
То есть числа
8, 15 и 17
образуют пифагорову тройку.
92 + 402 = 81 + 1600
92 + 402 = 1681
92 + 402 = 412
То есть числа
9, 40 и 41
образуют пифагорову тройку.
202 + 212 = 400 + 441
202 + 212 = 841
202 + 212 = 292
То есть числа
20, 21 и 29
образуют пифагорову тройку.
122 + 352 = 144 + 1225
122 + 352 = 1369
122 + 352 = 372
То есть числа
12, 35 и 37
образуют пифагорову тройку.
112 + 602 = 121 + 3600
112 + 602 = 3721
112 + 602 = 612
То есть числа
11, 60 и 61
образуют пифагорову тройку.
Если
(a; b; c)
– пифагорова тройка, то
(ka; kb; kc)
– тоже пифагорова тройка.
Если
(a; b; c)
– пифагорова тройка, то
a2 + b2 = c2
a2 + b2 = c2 | ∙ k2
k2 ∙ a2 + k2 ∙ b2 = k2 ∙ c2
(ka)2 + (kb)2 = (kc)2
Значит,
(ka; kb; kc)
является пифагоровой тройкой.
Например:
(6; 8; 10) = (2 ∙ 3; 2 ∙ 4; 2 ∙ 5)
(9; 12; 15) = (3 ∙ 3; 3 ∙ 4; 3 ∙ 5)
(30; 40; 50) = (10 ∙ 3; 10 ∙ 4; 10 ∙ 5)
где (3; 4; 5) является пифагоровой тройкой.
(10; 24; 26) = (2 ∙ 5; 2 ∙ 12; 2 ∙ 13)
где (5; 12; 13) является пифагоровой тройкой.
(16; 30; 34) = (2 ∙ 8; 2 ∙ 15; 2 ∙ 17)
где (8; 15; 17) является пифагоровой тройкой.
⠀
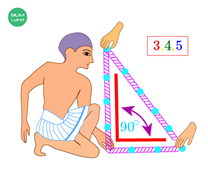
Прямоугольный треугольник с соотношением сторон
3 : 4 : 5
называют египетским.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
