
муниципальльное бюджетное общеобразовательное учреждение «Пустошкинский центр образования»
г. Пустошка
Псковская область
Методическая разработка урока математики в 6 классе
Автор: Горбачева И.В.,
учитель математики
МБОУ «Пустошкинский центр образования»
г. Пустошка
2020
Тема урока: Длина окружности
Класс: 6
Учебник: «Математика-6»/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2015
Тип урока: Урок «открытия» нового знания
Оборудование и материалы к уроку: компьютер, проектор, презентация к уроку, интерактивная доска, на каждой парте: нитки, кружочки из цветной бумаги различных радиусов.
Цели урока:
Развивающие: Развитие умения опытным путем получить зависимость между длиной окружности и её диаметром, выводить формулы длины окружности, применить их для решения практических задач, расширить кругозор учащихся. Развитие приемов умственной деятельности, памяти, внимания, умения сопоставлять, делать выводы.
Образовательные: расширение понятийной базы за счет включения в нее новых элементов. Повторение и закрепление приобретенных знаний по теме «Окружность. Развитие способности к критическому мышлению. Развитие коммуникативной компетенции учащихся. Развитие социо-культурной компетенции учащихся. Умение применять математические знания к решению задач. Демонстрация тесной связи математики с повседневной жизнью.
Воспитательные: Воспитание культуры личности, отношения к математике, как к части общечеловеческой культуры, играющей особую роль в общеобразовательном развитии. Воспитание ответственности, самостоятельности, умения работать в коллективе, паре, самостоятельно. Воспитание уважения друг к другу. Показать математику, как интересную науку, превратить занятие в необычный урок, где может проявить себя каждый человек. Воспитание ответственности, аккуратности и самостоятельности.
Планируемые результаты:
Личностные:
Самоопределение: рефлексивная самооценка учебной деятельности;
Смыслообразование: мотивация образовательной деятельности на основе демонстрации презентации и проблемных ситуаций; самостоятельность в приобретении новых знаний и практических умений;
Нравственно-этическое оценивание: воспитывать уважение к математике, умение видеть математические задачи в окружающем нас мире.
Регулятивные:
Овладение навыками самостоятельного приобретения новых знаний, организации учебной деятельности, постановки цели, планирования, самоконтроля и оценки результата своей деятельности.
Коммуникативные:
Формирование умений работать в группе с выполнением различных социальных ролей, представлять и отстаивать свои взгляды и убеждения, вести дискуссию, развитие монологической и диалогической речи, умения выражать свои мысли и выслушивать собеседника, воспитание сдержанности, культуры взаимоотношений;
Познавательные:
Приобретение опыта самостоятельного поиска и анализа информации путем практических действий, развитие мышления и внимания учащихся.
Ход урока
1. Организационный момент
Проверить готовность обучающихся к уроку (наличие инструментов). Приветствие. Создание благоприятной обстановки.
Ребята, здравствуйте!
Сегодня мы с вами в очередной раз убедимся в том, что математика – наука точная и интересная. Хочется, чтобы каждый из вас в математике для себя сделал хотя бы небольшое, но открытие.
2. Вводное слово. Самоопределение к деятельности. Формулировка темы
- Ребята, послушайте стихотворение. В нём будет спрятана загадка. Если вы её отгадаете, то узнаете, о чём пойдёт речь сегодня на уроке.
 Если видишь в небе
солнце,
Если видишь в небе
солнце,
Или чашку с молоком,
Видишь бублик или обруч,
Слышишь сказку с колобком.
В круге зеркала увидел
Ты сейчас свою наружность
И вдруг понял, что фигура
Называется ………………
Окружность!
А я вот очень люблю круглые клумбы, но затрудняюсь её померить.
Метром не получается. Может вы подскажите мне как это сделать?
А как измерить круглую клумбу?
Дети отвечают на вопрос предлагая варианты: измерительная лента,
проволока, нитка и др.
Спасибо, что подсказали.
- Сегодня мы научимся … (дети формулируют тему урока) искать длину окружности.
3. Этап подготовки
Запишем в тетради число и тему урока.
Выполните следующие задания в тетради. Позже поменяйтесь тетрадями и выполните проверку (подбираются задания, с помощью которых повторяется необходимый материал). Желающие зачитывают ответы.
|
А |
7 |
0,5 |
3 |
|
В |
28 |
2 |
12 |
 (≈19,3
и ≈20).
(≈19,3
и ≈20).
4. Актуализация знаний и умений
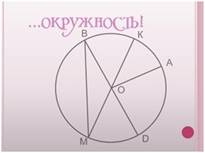
Внимательно рассмотрите чертеж и ответьте на вопросы
1. Что такое окружность и круг?
2. Как называется отрезок ОА для окружности? Есть ли ещё на рисунке радиусы? Назовите их.
3. Что такое радиус?
4. Есть ли на рисунке диаметр окружности?
5. Будет ли ВМ диаметром? Почему?
6. Если ОА=3см, найдите КМ и ВD.
7. Как соотносятся радиус и диаметр?
8. Что такое центр окружности?
9.
5. Постановка учебной задачи
А) Исследование: Как измерить длину окружности?
- Окружность нельзя измерить линейкой. Куда её приложить? Давайте представим себе, что наш класс это научно-исследовательская лаборатория. А мы – исследователи. Что мы можем сделать? (обсуждение)
Практическая работа (работа в паре)
- Возьмите нитку, обвяжите ею кружочек, а потом измеряйте длину нити линейкой. Получилась длина окружности. Обозначается она латинской буквой С. Запишите в тетради результаты своих измерений: С=…
Теперь измерьте диаметр, как можно точнее! Запишите измерения: d=…
Выполните деление величины С на величину d
и запишите:![]()
Результаты вычислений в практической работе заносятся обучающимися в таблицу на интерактивной доске:
|
|
R |
D |
C |
C/D |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
Вывод: какими бы различными не были окружности, отношения их длин к диаметрам будут постоянно одинаковыми. Т.е. длина окружности прямо пропорциональна длине её диаметра.
Б) Число П
Число, которое мы получили, математики договорились
обозначать греческой буквой π («пи»). ![]() ; π = 3,1415926…≈3,14.
Точного значения числа π нет. Что знают ваши родители об этом числе?
(обсуждение)
; π = 3,1415926…≈3,14.
Точного значения числа π нет. Что знают ваши родители об этом числе?
(обсуждение)
История нахождения числа π длилась
тысячелетия. Отношение длины окружности к её диаметру есть величина постоянная.
Это было показано Архимедом, он доказывает, что число π меньше чем ![]() , но больше чем
, но больше чем ![]() . В наши дни с
помощью ЭВМ число π вычислено с точностью до миллиона знаков, но в жизни
такая точность не нужна. Вполне достаточно десяти знаков.
. В наши дни с
помощью ЭВМ число π вычислено с точностью до миллиона знаков, но в жизни
такая точность не нужна. Вполне достаточно десяти знаков.
Как запомнить это число?
На этот вопрос есть много различных ухищрений. Вот только некоторые из них:
Двадцать две совы
скучали
На семи сухих ветвях.
Двадцать две совы мечтали
О семи больших мышах.
Надо только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Это я знаю и помню прекрасно,
Те многие знаки мне лишни, напрасны.
(Количество букв в каждом слове соответствует цифре в числе π.)
Во всем мире отмечается один из самых необычных праздников — Международный день числа «Пи» (International π Day).
Задача: Сейчас в своих гаджетах найдите информацию об этом празднике
Обобщение полученной информации: Впервые День был
отмечен 14 марта в 1987 году в научно-популярном музее Эксплораториум в
Сан-Франциско (San Francisco Exploratorium).
Этот неофициальный праздник придумал физик из Сан-Франциско Ларри Шоу
(Larry Shaw), который заметил, что в американской системе записи дат (месяц /
число) дата 14 марта — 3/14 — и время 1:59 совпадает с первыми разрядами числа
π = 3,14159…. Примечательно, что в этот же день родился Альберт Эйнштейн —
создатель теории относительности.
Поскольку
в последовательности знаков числа пи нет повторений – это значит, что
последовательность знаков пи подчиняется теории хаоса, точнее, число пи – это и
есть хаос, записанный цифрами.
Или другой пример: если зашифровать все буквы цифрами, то в
десятичном разложении числа пи можно найти всю мировую литературу и науку, и
рецепт изготовления соуса бешамель, и все священные книги всех религий. Там
содержится не только вся мировая литература, которая уже написана, но и все
книги, которые еще будут написаны. Получается, что это число (единственное
разумное число во вселенной!) и управляет нашим миром.
В этот день люди, любящие математику или математиков читают
хвалебные речи в честь числа π, его роли в жизни человечества, рисуют
антиутопические картины мира без π, играют в игры, начинающиеся на «пи»,
решают математические головоломки и загадки, водят хороводы вокруг предметов,
связанных с этим числом, выпекают большие круглые пироги («pie») с изображением
греческой буквы «пи» и с первыми цифрами самого числа.
В) Вывод формул:
Вернёмся к формуле: ![]() .
Отсюда выведем формулу длины окружности: С = πd. А если учесть, что d =
2r, то С = 2πr.
.
Отсюда выведем формулу длины окружности: С = πd. А если учесть, что d =
2r, то С = 2πr.
Из этих формул легко получить формулы по
которым вычисляются диаметр и радиус окружности, если известна её длина: ![]() и
и![]() .
.
6. Физкультминутка.
А теперь ребята встали,
Быстро руки вверх подняли,
В стороны, вперед, назад,
Повернулись влево, вправо,
Тихо сели, вновь за дело.
7. Применение знаний и умений в новой ситуации
а) Вычислите длину окружности, диаметр которой равен 10 см; 2,5 м. (Возьмите π ≈ 3,14.)
б) Вычислите длину окружности, радиус которой равен 7,5 см; 5 м. (Возьмите π ≈ 3.)
в) Найдите длину выделенной дуги окружности.
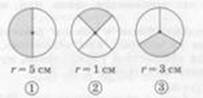
Обсуждение полученных ответов
8. Домашнее задание
a. Кто ввел обозначение П и почему оно такое?
b. На сколько метров голова пройдет больше, чем ноги, если мы пройдем по экватору вокруг Земли? (радиус Земли – 6400 км)
9. Рефлексия
А сейчас давайте вспомним, что сегодня на уроке мы:
1. ПОВТОРИЛИ (что такое окружность, радиус, диаметр, как они связаны друг с другом)
2. УЗНАЛИ (формулы, по которым вычисляется длина окружности, что такое число π)
3. ЗАКРЕПИЛИ (научились применять эти формулы при решении задач)
- Почему число П особенное?
Все ребята получают в подарок закладку с основным материалом урока.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.