Разработка урока в соответствии с требованиями ФГОС. Тема: «Решение текстовых задач на концентрацию различными способами»

Разработка урока в соответствии с требованиями ФГОС.

Тема: «Решение текстовых задач на концентрацию различными способами. Задачи В.11»

Дата проведения:17.05.2014г.

Предмет: алгебра и начала анализа.

Класс:11 «а».

Учитель: Стригина Светлана Викторовна, учитель математики МБОУ СОШ№7 г.Беслана.

Используемая технология: проблемно-поисковая форма организации учебной деятельности

Цели урока:

1. Существенно расширить круг алгебраических задач с химическим содержанием.

2. Формировать умения переноса знаний с одного предмета на другой.

3. Научить делать осознанный выбор способа и метода решений задач.

4. Развивать познавательный  интерес, реализуя межпредметные связи курсов химии и математики.

5. Воспитывать коммуникативные способности и умение работать в группе.

Задачи урока:

1.     Рассмотреть в сравнении химический и математический способы решения задач с использованием понятия концентрация.

2.     Применить способы решения задач на практических примерах.

3.     Вывести новые методы решения задач на смеси и рассмотреть их применение на уроках математики и химии.

Тип урока: урок усвоения новых знаний.

Методы обучения: проблемный, частично-поисковый, наглядный.

Формы деятельности учащихся: коллективная форма деятельности, самостоятельная и фронтальная работа.

Оборудование: экран, проектор, презентация, раздаточный материал, компьютер.

Этапы урока

1. Организационный

2.Актуализация знаний. Ситуация успеха.

3.Учебная ситуация (задание –«ловушка»)

4. Рефлексия деятельности.

5.Порождение нового способа. 

6. Рефлексия действий при порождении нового способа.

7.Самостоятельная работа учащихся.

8. Подведение итога урока.

Ход урока.

I этап Организационный момент.

Концентрация внимания обучающихся и ориентирование на работу.

II этап. Актуализация опорных знаний. Ситуация успеха.

Цель: проверка знаний учащихся, создание ситуации успеха, мотивирующей учащихся на дальнейшую работу.

Устная работа

1.     Что называется процентом?

2.     Перевести проценты в десятичную дробь.

30% = 0.3

65% = 0.65

84% = 0.84

103% = 1.03

6% = 0.06

3.2% = 0.032.

               3. Перевести десятичные дроби в проценты.

                          0,07 = 7%

0.21        = 21%

                          2.3 = 230%

                     0.2=20%

                     1=100%

4.Дать  определение концентрации раствора.

Определение. Концентрация раствора – это часть, которую составляет  масса растворимого вещества от массы  всего раствора.                                           В толковом словаре концентрация (лат сопс- centrum) – центр, сосредоточение.

5        Что означает 9% концентрация раствора поваренной соли. (В 100г раствора содержится 9г. соли.)                                                                          Во многих текстовых задачах понятие «концентрация» может быть заменено на «жирность» (масло, молоко), «крепость» (уксус, вино), «проба» (золото).

6.Как понять? Жирность молока равна 3,2%.Крепость уксуса -9%.Проба золота - 583.

7.В «Занимательной алгебре» Я.И. Перельмана есть любопытная задача под названием: «В парикмахерской»:

Задача: Может ли алгебра понадобиться в парикмахерской? Оказывается, такие случаи бывают. Мне пришлось убедиться в этом, когда однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:

-Не поможете ли нам разрешить задачу, с которой мы никак не справимся?

- Уж сколько раствора испортили из-за этого!- добавил другой

- В чем задача?

- У нас имеется два раствора перекиси водорода: 30%- ыйи 3 % -ый. Нужно их смешать так, чтобы составился 12% -ый раствор. Не можем подыскать правильной пропорции.

Мне дали бумажку, и требуемая пропорция была найдена. А как это сделать?

III этап. Учебная ситуация (задание – «ловушка»).

Цель: организация  «сбоя»  в деятельности обучающихся.

Обучающиеся легко справляются с заданиями №1-6, а  задание №7  вызывает у  обучающихся затруднение.

Выполняя данное задание, учащиеся или ошибочно выполняют его, или получают «явный сбой» (т.е. у учащихся не хватает средств для решения данной задачи).

IV этап.  Рефлексия.

Цель: вывести учащихся в рефлексивную позицию.

 Коллективная форма деятельности учащихся.

Учитель организует коммуникативное взаимодействие учащихся, фиксирует несостоятельность или проблематичность использования  тех или иных методов решения, предлагаемых учащимися.  Учащиеся предлагают известные им методы решения. При выдвижении каждого способа учащиеся попадали в рефлексивную ситуацию. Учащиеся пытаются выполнить задание известным им способом,  но обнаруживают в нем недостатки.

 Итак, вы догадались, что тема урока « Решение текстовых задач на концентрацию». Эти задачи довольно часто встречаются в ЕГЭ, задачи  В12. Для того, чтобы научиться решать задачи, надо научиться такому подходу к задаче, при котором задача выступает как объект тщательного изучения, а ее решение – как объект конструирования изобретателя. Древние говорили: «Научить нельзя, можно только научиться». Помните всегда об этом.

 Чтобы лучше понимать условия задач на концентрацию, смеси и сплавы необходимо знать следующие понятия:

o   Все получающиеся сплавы или смеси однородны.

o  При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.

o   Процент - одна сотая часть любого вещества. 

o   Процентным содержанием (концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе.  Это отношение может быть выражено либо в дробях, либо в процентах.

o   Сумма концентраций всех компонентов, составляющих смесь, равна.

           Рассмотрим задачу.

Нальем в стакан 150 г воды и добавим 50 г сахара. Какой станет концентрация раствора?

Обозначим Мобщ. – общая масса раствора     150+50=200г.

                       Мч.в.  – масса чистого вещества    50г.

                       К           - концентрация вещества    50/200=1/4

Выразим эту величину в процентах  ¼ * 100% = 25%

Представим функциональную зависимость величин входящих в задачи о смесях, растворах в виде следующей математической модели:

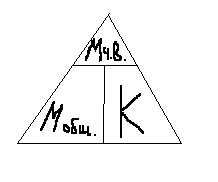
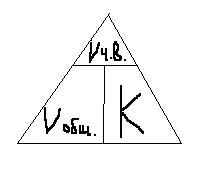
Мч.в=Мобщ.*К                               Vч.в=Vобщ.*К

Мобщ.=Мч.в/К                               Vобщ.=Vч.в/К

К= Мч.в/Мобщ.                               К=Vч.в/Vобщ

Задача №1

 Один раствор содержит 30% по массе азотной кислоты, второй 55% азотной кислоты. Сколько нужно взять 1-го и 2-го раствора, чтобы получить 100 кг. 50% раствора азотной кислоты?