Реферат «Компьютерное моделирование и решение нелинейных уравнений»

 

РЕФЕРАТ

Компьютерное моделирование и решение нелинейных уравнений

 

1.            Динамические системы и построение математической модели

 

 

Динамические системы – это системы, в которых входные переменные являются функциями от времени или каких-либо других параметров. Описываются эти системы дифференциальными и интегральными уравнениями. Например, большая часть законов механики, электротехники, теории упругости, теории управления и т.д. описываются с помощью дифференциальных уравнений.

На практике динамические системы встречаются очень часто. Моделирование систем, связанных с движением тел, с расчетом потоков энергии, с расчетом потоков материальных ресурсов, с расчетом оборотов денежных средств и т.д. в конечном счете, сводится к построению и решению дифференциальных уравнений (как правило, II-го порядка).

Прямолинейное движение тела, движущегося под действием переменной силы F(t,S,) ,где S=S(t), описывается дифференциальным уравнением второго порядка в форме уравнения Ньютона:

 m ‧= F(t,S,), где

m - масса тела,

S - перемещение тела,

 -линейная скорость,

 -линейное ускорение.

При этом задаваемые начальные условия S|_t=0=S₀, ,|_t=0=,₀  имеют четкий физический смысл. Это - начальное положение тела и его начальная скорость.

Вращательное движение тела под действием крутящего момента M_кр(t,φ,) где φ = φ (t), описывается аналогично Iρ‧=M(t, φ, )  где

Iρ - полярный момент инерции тела,

φ  -угол поворота,

 - угловая скорость,

 - угловое ускорение.

При построении математических моделей систем, машин, механизмов с учетом колебаний, возникающих в них, также необходимо построить и решить дифференциальное уравнение, т.к. все виды колебаний (свободные гармонические, вынужденные) также описываются дифференциальными уравнениями.

На практике лишь небольшое число дифференциальных уравнений допускает интегрирование в квадратурах. Еще реже удается получить решение в элементарных функциях. Поэтому большое распространение при решении математических моделей с помощью ЭВМ получили численные методы решения дифференциальных уравнений.

Нахождение определенного интеграла в процессе моделирования объектов процессов или систем может применяться в следующих задачах:

1.            Определение пути при переменной скорости:

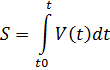
2.            Нахождение скорости при переменном ускорении: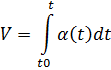

3.            Определение моментов инерции тел:

 

4.            Нахождение работы переменной силы: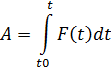

 

5.            При решении дифференциальных уравнений.

Итак, дана функция y=f(x).

Найти интеграл этой функции на участке [a,b], т.е. найти

 

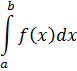
Если подынтегральная функция f(x) задана в аналитическом виде;

Если функция f(x) непрерывна на отрезке [a,b] ;

если известна ее первообразная, т.е.

Fʹ(x)=f(x), xϵ [a,b],

То интеграл может быть вычислен по формуле Ньютона-Лейбница как приращение первообразной на участке [a,b], т.е.

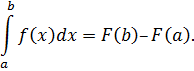
Но на практике формула Ньютона-Лейбница для вычисления интеграла используется редко. Численные методы интегрирования применяются в следующих случаях:

1.            подынтегральная функция f(x) задана таблично на участке [a,b] ;

2.            подынтегральная функция f(x) задана аналитически, но ее первообразная не выражается через элементарные функции;

3.            подынтегральная функция f(x) задана аналитически, имеет первообразную, но ее определение слишком сложно.

В численных методах интегрирования не используется нахождение первообразной. Основу алгоритма численных методов интегрирования составляет геометрический смысл определенного интеграла. Интеграл численно равен площади S криволинейной трапеции, расположенной под подынтегральной кривой f(x) на участке [a,b] (рис.1).

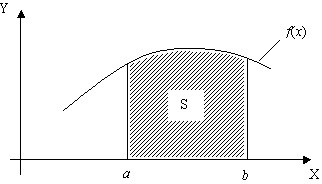
Рисунок 1 – Геометрический смысл определенного интеграла

 

Суть всех численных методов интегрирования состоит в приближенном вычислении указанной площади. Поэтому все численные методы являются приближенными.

При вычислении интеграла подынтегральная функция f(x) аппроксимируется интерполяционным многочленом. На практике чтобы не иметь дело с многочленами высоких степеней, весь участок [a,b] делят на части и интерполяционные многочлены строят для каждой части деления.

Порядок вычисления интеграла численными методами следующий (рис.2):

1.            Весь участок [a,b] делим на n равных частей с шагом h=(b-a)/n.

2.            В каждой части деления подынтегральную функцию f(x) аппроксимируем интерполяционным многочленом. Степень многочлена n = 0,1,2:

3.            Для каждой части деления определяем площадь частичной криволинейной трапеции.

4.            Суммируем эти площади. Приближенное значение интеграла I равно сумме площадей частичных трапеций

 

I =

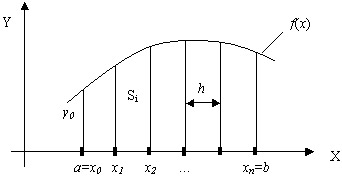
Рисунок 2 – Вычисление определенного интеграла

 

Нахождение приближенного значения интеграла называется квадратурой, а формулы для приближенного вычисления интеграла - квадратурными формулами или квадратурными суммами.

Разность R между точным значением интеграла и приближенным значением называется остаточным членом или погрешностью квадратурной формулы, т.е.

 –

Если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом нулевой степени, т.е. прямой, параллельной оси OX, то квадратурная формула называется формулой прямоугольников, а метод – методом прямоугольников.

Если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом первой степени, т.е. прямой, соединяющей две соседние узловые точки, то квадратурная формула называется формулой трапеций, а метод – методом трапеций.

Если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом второй степени, то квадратурная формула называется формулой Симпсона, а метод – методом Симпсона.

 

 

2. Метод прямоугольников

 

Словесный алгоритм метода прямоугольников:

1.            Весь участок [a,b] делим на n равных частей с шагом h=(b-a)/n.

2.            Определяем значение y_i подынтегральной функции f(x) в каждой части деления, т.е.

y_i = f(x_i), I = .

3.            В каждой части деления подынтегральную функцию f(x) аппроксимируем интерполяционным многочленом степени n = 0, т.е. прямой, параллельной оси OX. В результате вся подынтегральная функция на участке [a,b] аппроксимируется ломаной линией.

4.            Для каждой части деления определяем площадь S_i частичного прямоугольника.

5.            Суммируем эти площади. Приближенное значение интеграла I равно сумме площадей частичных прямоугольников.

Если высота каждого частичного прямоугольника равна значению подынтегральной функции в левых концах каждого шага, то метод называется методом левых прямоугольников (рис.3). Тогда квадратурная формула имеет вид

I =

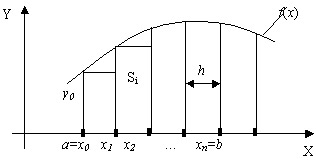
Рисунок 3 – Метод левых прямоугольников

Если высота каждого частичного прямоугольника равна значению подынтегральной функции в правых концах каждого шага, то метод называется методом правых прямоугольников (рис.4). Тогда квадратурная формула имеет вид

I =

 

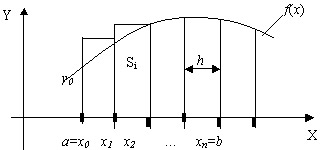
Рисунок 4 – Метод правых прямоугольников

Точность каждого метода прямоугольников имеет порядок h.

 

Алгоритм вычисления интеграла построим в виде итерационного процесса поиска с автоматическим выбором шага. На каждом шаге будем уменьшать шаг в два раза, то есть увеличивать число шагов n в два раза. Выход из процесса поиска организуем по точности вычисления интеграла. Начальное число шагов n=2. Схема алгоритма методов прямоугольников представлена на (рис. 5).

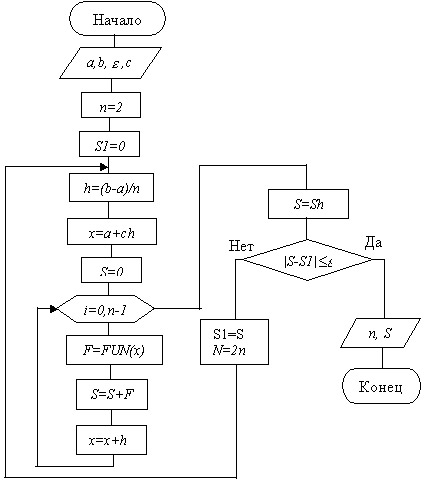
Рисунок 5 – Схема алгоритма метода прямоугольников (с автоматическим выбором шага)

 

Условные обозначения:

a,b – концы интервала,

ε – аданная точность,

с=0 – метод левых прямоугольников,

с=1 – метод правых прямоугольников,

S1 – значение интеграла на предыдущем шаге,

S – значение интеграла на текущем шаге.

На рисунке 6 представлена реализация метода прямоугольников в среде моделирования MathCad.

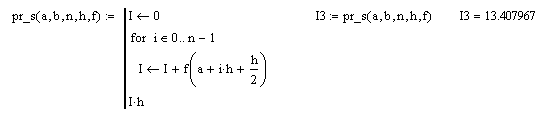
Рисунок 6. – Реализация метода прямоугольников в среде моделирования MathCad

3.            Метод трапеций

 

Словесный алгоритм метода трапеций:

1.            Интервал [a,b] делим на n равных частей с шагом h=(b-a)/n.

2.            Вычисляем значение подынтегральной функции в каждой узловой точке

 y_i =f(x), i = .

3.            На каждом шаге подынтегральную функцию f(x) аппроксимируем прямой, соединяющей две соседние узловые точки. В результате вся подынтегральная функция на участке [a,b] заменяется ломаной линией проходящей через все узловые точки.

4.            Вычисляем площадь каждой частичной трапеции.

5.            Приближенное значение интеграла равно сумме площадей частичных трапеций, т.е.

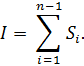
Найдем площади S_i частичных трапеций:

         S₀ = h(y₀+ y₁),

         S₁ = h(y₁+ y₂),

S₂ = h(y₂+ y₃),

         …

S_n = h(y_n-1+ y_n),

Приближенное значение интеграла равно

 

 

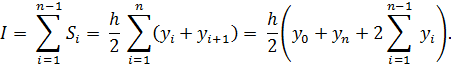
Точность метода трапеций имеет порядок h².

Схема алгоритма метода трапеций представлена на рисунке 7

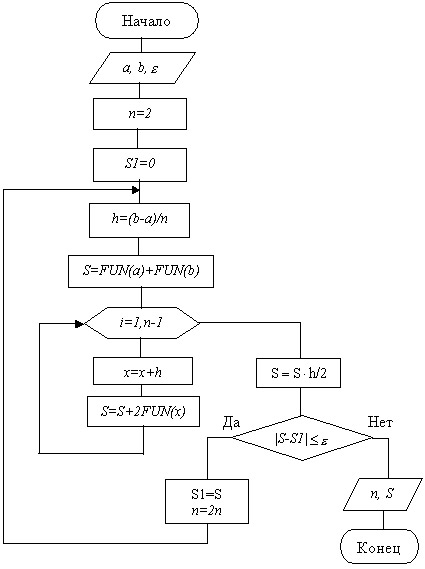
Рисунок 7 – Схема алгоритма метода трапеций (с автоматическим выбором шага)

На рисунке 8 представлена реализация метода трапеций в среде моделирования MathCad.

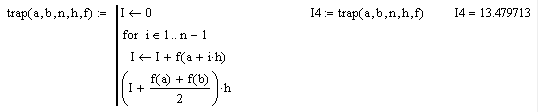
Рисунок 8. – Реализация метода трапеций в среде моделирования MathCad.

4.            Метод Симпсона

 

В методе Симпсона в каждой части деления подынтегральная функция аппроксимируется квадратичной параболой a₀x²+a₁x+a₂. В результате вся кривая подынтегральной функции на участке [a,b] заменяется кусочно-непрерывной линией, состоящей из отрезков квадратичных парабол. Приближенное значение интеграла I равно сумме площадей под квадратичными параболами.

Т.к. для построения квадратичной параболы необходимо иметь три точки, то каждая часть деления в методе Симпсона включает два шага, т.е.

L_k=2h.

В результате количество частей деления N2=n/2. Тогда n в методе Симпсона всегда четное число.

Определим площадь S₁ на участке [x₀, x₂]

Исходя из геометрического смысла определенного интеграла, площадь S₁ равна определенному интегралу от квадратичной параболы на участке [x₀, x₂]:

S₁ = ++=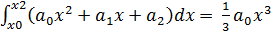

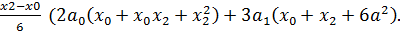
Неизвестные коэффициенты квадратичной параболы а₀ , а₁, а₂ определяем из условия прохождения параболой через три узловых точки с координатами (x₀y₀), (x₁y₁), (x₂y₂).

На основании этого условия строим систему линейных уравнений:

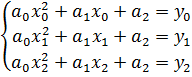
Решая эту систему, найдем коэффициенты параболы.

В результате имеем: S₁ = ..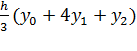

Для участка [x₂, x₄]:  S₂ = ..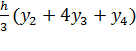

Для участка [x_i-1, x_i+1]: ., S_k = ..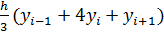

Где  k =.

Суммируя все площади S₁ под квадратичными параболами, получим квадратурную формулу по методу Симпсона:

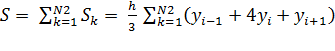  , где

N2 - количество частей деления.

Точность метода Симпсона имеет порядок (h³/h⁴).

Схема алгоритма метода Симпсона:

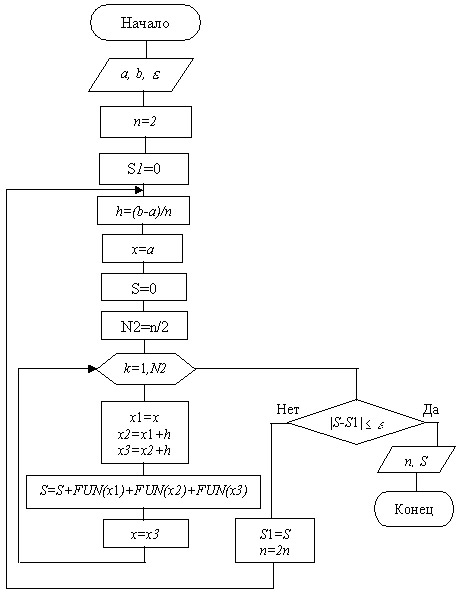
Рисунок 9 – Схема алгоритма Симпсона (с автоматическим выбором шага)

На рисунке 10 представлена реализация метода Симпсона в среде моделирования MathCad.

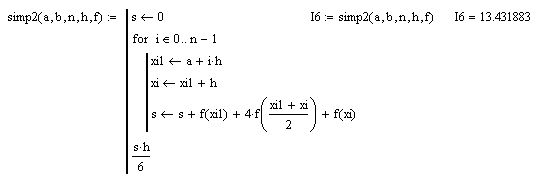
Рисунок 10. – Реализация метода Симпсона в среде моделирования MathCad

Список используемой литературы

 

1. Динамические системы. Среда. Методы решения задач. Учебное пособие/ Гуз С.Н., Дегтяр С.Н. – Мозырь: МГПУ, 2002.

2. Демидович Б.П. Сборник задач и упражнений по математическому анализу. - М.: Наука, 1969. – 544 с.

3. Дьяконов В.П. Математические модели и их построение 2000: учебный курс. – СПб.: Питер, 2000.

4. Кирьянов Д.В. Математические модели и их построение. – СПб.: БХВ-Петербург, 2003.

6. Очков В.Ф. Методы решения нелинейных уравнений. - М.: Компьютер пресс, 1998. - 380 с.

 

Скачано с www.znanio.ru