Министерство общего и профессионального образования Ростовской области
	государственное бюджетное профессиональное образовательное учреждение Ростовской области «Ростовский колледж металлообработки и автосервиса» (ГБПОУ РО «РКМиА»)

 

 

 

РЕГИОНАЛЬНЫЙ  КОНКУРС СТУДЕНЧЕСКИХ ПРОЕКТОВ

«МАТЕМАТИКА В МОЕЙ ПРОФЕССИИ»

РЕФЕРАТ

ТЕМА. « Математика в профессии Автомеханик»

 

 

 

 

                                                                   Выполнил:

                                                                   студент 1   курса    ТО 23-17                                                                                     

                                                                   Вербин Вячеслав Константинович

                                                                   Руководитель проекта:

                                                                   преподаватель математики

                                                                   Филиппова Ольга Львовна

 

 

 

 

 

2021

 

 

Оглавление

Оглавление                                                                                                   2

Введение                                                                                                        3

Арифметические действия                                                                           4

Пропорции и проценты                                                                                 5

Окружность и круг                                                                                        7

Параллельность: прямых, прямой и плоскости                                           8

Векторы                                                                                                          9

Тригонометрия                                                                                               11

Функции и графики                                                                                       13

Заключение                                                                                                  14

Литература                                                                                                   15

Приложение                                                                                                  16

     

 

 

 

 

 

 

 

 

 

 

 

 

Введение

«Математика играет весьма существенную    роль в формировании нашего духовного облика.»

Г. Вейль

Весь наш мир состоит из математики. Везде присутствуют числа и счет. Многие часто задаются вопросом зачем нужна математика? Нередко сам факт того, что эта дисциплина входит в обязательную программу университетов и школ, ставит людей в недоумение.

Это недоумение выражается в следующем: Мол, для чего мне, человеку чья будущая (или нынешняя) профессия не будет связана с ведением расчетов и применением математических методов, знать математику?

           Когда мне посоветовали взять эту тему, я не отказался, потому что я посчитал, что она очень интересна.

В своем проекте я хочу показать и рассказать, что моя профессия неразрывно связана с математикой, что  она нужна в моей профессии, на каждом шагу.

 Цели проекта:

·                   показать разнообразие профессиональных задач, решаемых математическими    методами;

·                   развить познавательные интересы, творческий коммуникативные способности определяющие формирование компетентной личности, способной к жизни деятельности, самоопределению в информационном обществе;

·                   научиться правильно решать возникающие конкретные задачи; 

·                   самостоятельно добывать знания и их совершенствовать.

 Задачи:  

·                   приобретение знаний о структуре исследовательской деятельности;

·                   способа поиска необходимой для исследования информации;    

·                   создание благоприятных условий для самостоятельной творческой поисковой исследовательской деятельности.

Актуальность.

Обучаясь математики студенты часто не понимают ,зачем это нужно? Где в конкретной ситуации они смогут применить полученные знания. Математика  считается одной из сложных дисциплин. Многие студенты ни в силах соотнести строгость и математические понятия с реальной жизнью, они не понимаю где в окружающей действительности им могут  пригодиться знания , полученные на занятиях математики.

Мой проект  показывает применение математических знаний в окружающей действительности, направлен на удаления противоречия между наличием прочных, теоретических знаний и неспособностью применить это на практике.

 

 

 

Арифметические действия.

 

Задача 1.1. Рассчитать коэффициент сопротивления качению

f = f₀ + kv², k = 7 · 10^–6,

где f₀ – коэффициент сопротивления качению при малой скорости для разных моделей автомобилей и разных скоростей движения. Интенсивный рост коэффициента f₀ начинается при v = 20...30 м/с.

 Построить график зависимости f₀ от v(таблица 3). Мощность теряемая при качении в значительной степени идёт на нагрев шин и износ протектора,есть снижает их надёжность[2, стр 362].

Задача 1.2.  

При выбеге (нейтральное положение в коробке передач) потери в трансмиссии определяют силой Р_тр, приведённой к ведущим колесам. Силу определяют экспериментально методом выбега при вывешенных колёсах автомобиля. Она описывается линейной зависимостью Р_тр = Р_тр0 + k_трV.

Мощность N_тр, теряемая в трансмиссии при выбеге: N_тр = Р_трV 10 ^{– 3}.

V – скорость автомобиля.

Рассчитать силу Р_тр  и мощность N_тр в зависимости от изменения скорости автомобиля. Построить график линейной зависимости силы Р_тр от скорости, график зависимости силы Р_тр от мощности N_тр и график расхода горючего, если учесть, что чем больше потери мощности, тем больше расход горючего (трансмиссия).  

Ниже (см. табл.4) приведены значения сил Р_тр0  и коэффициентов  k_тр для разных автомобилей, k_тр – коэффициент, учитывающий влияние скорости на силу трения.

Задача 1.3.  

Рассчитать силу сопротивления воздуха для разных моделей автомобилей и при различных скоростях v их движения. Р_в – сила сопротивления воздуха, Р_в = k_в F_в v². k_в – коэффициент сопротивления воздуха, F_в – лобовая площадь  автомобиля.(таблица 6)

Задача 1.4.  

Для разных моделей автомобилей найти площадь занимаемой площадки и размеры гаража.(табл. 5)

Задача 1.5.  

Преодолеет ли автомобиль (разные модели.(табл. 5)) препятствие высотой Н_с = 0,13; 0,25 метра? Максимальная высота преодолеваемой колесом автомобиля стенки:

для полноприводных автомобилей 4×4 Н_с £ ½ r_c,

для специальных автомобилей 8×8 Н_с £ r_c,

для грузовых автомобилей Н_с £ 0,15 rc.

Радиус колеса r_c = 320; 340; 360; 380 мм.

 

Задача 1.6.  

Преодоление рва автомобильным колесом диаметром Dс зависит от глубины рва h_n и выражается длиной хорды В_р:

В_р = 2 √ (D_с h_n – h_n²),

для одиночного колеса Вр £ 0,7 Dс.

Определить возможность преодоления автомобилем с разным типом шин (см. табл. 1) рва глубиной 0,17; 0,25; 0,38 метра.

Задача 1.7.  

По техническим характеристикам рассчитать литраж V_л двигателя указанного автомобиля[2, стр 161].

V_л = V_n n,

где V_n – рабочий объём цилиндра (V),

n – число цилиндров двигателя.

 

 

Пропорции и проценты.

Задача 1.8.  

Известно, что при увеличении относительной влажности воздуха на 10% эффективная мощность двигателя снижается на 0,75%, а расход топлива увеличивается на 3,75%.

 

Задача 1.9.  

Автомобиль движется со средней скоростью из Ростова-на-Дону в Москву, расстояние между которыми составляет 1200 км. Сколько литров топлива потребуется автомобилю в дорогу, если учесть, что ⅓ пути он проехал при относительной влажности воздуха 60% рт. ст., ⅓ пути – при 80% рт. ст. и ⅓ пути – при 95%  рт. ст.

 

Задача 1.10.  

Какова будет мощность двигателя в дороге? Построить график зависимости относительной  влажности воздуха и мощности двигателя (пропорции линейной зависимости). Сделать вывод (уменьшается разгонная характеристика автомобиля).

Технические характеристики различных моделей автомобилей приведены в таблицах приложения.

Задача 1.11.  

На примере энергетического баланса можно показать пример прямой пропорциональности. Если V_h – рабочий объём двигателя; τ – коэффициент тактности, где τ = 2 для двухтактного и τ = 4 для четырёхтактного двигателей; n – частота вращения коленчатого вала двигателя, мин ^{– 1}; i – число цилиндров; Р_i – среднее индикаторное давление; М_i – индикаторный крутящий момент,

М_i = P_i i V_h / π r.

M_i прямо пропорционально P_i, т.е. P_i = L_i / V h.

 

Задача 1.12.  

Рассматривая работу коробки передач можно отметить, что крутящий момент на валах 1, 2, 3 планетарных механизмов относятся[2, стр 248].

М₁ : М₂ : М₃ = 1 : a :  – (1 + a)

a – передаточное число планетарного механизма.

Z – число зубьев в зубчатом колесе.

z₆

a =  ¾ = 1,4 ¸ 5                     (1)    

z₁

z₈       z₇

a =  ¾  ·  ¾ =  – (1 ¸ 8)            (2)

z₁       z₉

Окружность и круг

 

Размер радиальных шин обозначается тремя числами и буквой. Например, 175/70R13, где 175 – ширина профиля шины В, мм; 70 – отношение высоты Н профиля к ширине профиля В, %; R – условное обозначение радиальной шины; 13 – посадочный диаметр d, дюймы (см. рис. 1). Применяемые шины для некоторых марок автомобилей приведены в таблице 7. по формуле R = 12,7 d  + В × % / 100%.[2, стр 230].

Задача 1.13.  

Найти средний радиус шины для конкретной шины (см. табл.1).

Правилами дорожного движения запрещена эксплуатация автомобиля, если остаточная высота рисунка протектора на площади, ширина которой равна половине ширины беговой дорожки, а длина равна 1/6 окружности шины, меньше( рис 19 приложении):

1,6 мм – для легковых автомобилей;

2 мм – для автобусов;

1 мм – для грузовых автомобилей.

Задача 1.14.  

Определить для разных типов шин площадь контрольного участка.

( таблица 1)

2.  

Какую площадь составляет контрольный участок от площади беговой дорожки? Беговая дорожка – круг колеса с учётом ширины шины.

 

Параллельность прямых, прямой и плоскости.

Задача 2.1. (рис .20 в приложении)

Какие из прямых a, b, c, d, e, k, m:

a )                                                  лежат в плоскости a;

b )                                                  пересекают плоскость a;

c )                                                  параллельны плоскости a?

Задача 2.2.  

Назовите прямые, которые являются (см. рис.20):

a )                                                  пересекающимися;

b )                                                  параллельными;

c )                                                  скрещивающимися.

Задача 2.3.  

Назовите прямые, которые будут лежать в одной плоскости (см. рис.20). Ответ обоснуйте.

Задача 2.4.  

Рис. 2

Управляемые колёса,

установленные на автомобиле

с развалом в вертикальной плоскости

Какие из прямых a, b, c, d, h, k, l, m, n, q, p:

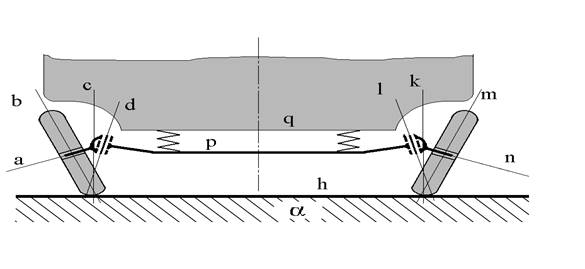a )                                                  лежат в плоскости a;

b )                                                  пересекают плоскость a;

c )                                                  параллельны плоскости a?

 

Задача 2.5.  

Назовите прямые, которые являются (см. рис. 2):

a )                                                  пересекающимися;

b )                                                  параллельными;

c )                                                  скрещивающимися.

 

Задача 2.6.  

Какие прямые (см. рис. 3) будут лежать в одной плоскости?

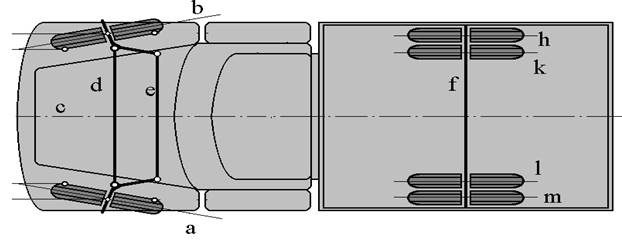
рис.3

Управляемые колёса,

 установленные на автомобиле

со схождением в горизонтальной плоскости

Какие из прямых a, b, c, d, e, f, h, k, l, m:

d )                                                  лежат в плоскости a;

e )                                                  пересекают плоскость a;

f )                                                   параллельны плоскости a?

 

Задача 2.7.  

Назовите прямые (см. рис. 3), которые являются:

d )                                                  пересекающимися;

e )                                                  параллельными;

f )                                                   скрещивающимися.

Векторы

 

 

1.                                                          По данным рисунка 22 назовите коллинеарные векторы.

2.                                                          Какие векторы будут перпендикулярны друг другу?

3.                                                          Разложите вектор G_a^→ по векторам P_n^→ и G_a^→cosa.

4.                                                          Начертите векторы G_a^→ и G_a^→cosa и постройте векторы, равные:

1.                                                                                                                      G_a^→ + G_a^→cosa;

2.                                                                                                                      G_a^→ - G_a^→cosa;

3.                                                                                                                      2G_a^→ + 3G_a^→cosa.

 

Задача 2.8.  

Рис. 4

 

Расчётные схемы для определения вертикальных реакций:

а – статических, для двухосного автомобиля;

б – динамических, для двухосного автомобиля;

в – динамических, для одноосного полуприцепа.

 

1.                                  По данным рисунка 4 назовите коллинеарные векторы.

2.                                  Какие векторы будут перпендикулярны друг другу?

3.                                  Разложите вектор G_a^→ по векторам P_n^→ и G_a^→cosa.

4.                                  Начертите векторы G_a^→ и G_a^→cosa и постройте векторы, равные:

1.                                                                                                                      G_a^→ + G_a^→cosa;

2.                                                                                                                      G_a^→ – G_a^→cosa;

3.                                                                                                                      2G_a^→ + 3G_a^→cosa.

 

 

1.                                  По данным рисунка 21 назовите коллинеарные векторы.

2.                                  Какие векторы будут перпендикулярны друг другу?

3.                                  Разложите:

вектор N^→ по векторам R_x^→ и R_z^→.

4.                                  Начертите векторы N^→  и R_x ^→ и постройте векторы, равные:

1.                                                                                                                      N ^→ + R_x ^→;

2.                                                                                                                      N ^→  –   R_x ^→;

3.                                                                                                                      2N ^→ + 3 R_x ^→;.

 

 

Тригонометрия

Задача 2.9.  

Радиус поворота автомобиля с жёсткими шинами (можно задать вопрос: в чём заключаются различия между эластичными и жёсткими шинами?) определяется по формуле:

R_n = L / tg q,

Рис. 5

где L – база автомобиля;

q – средний радиус поворота управляемых колёс (см. рис. 5).

Схема движения автомобиля с нейтральной степенью поворачиваемости

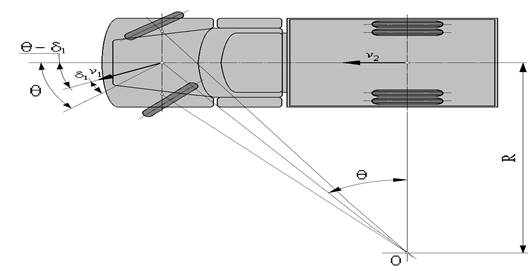на жёстких шинах:

d₁ – углы увода шин переднего моста; q - средний угол поворота; v₁ – вектор скорости переднего моста; v₂ – вектор скорости заднего моста; R – радиус поворота с жёсткими шинами.

По данным технических характеристик разных марок автомобилей (см. приложение №1) найти угол q.

Размер диагональной шины 6,95-16 (ширина 6,95 дюймов, посадочный диаметр 16 дюймов)

Размер радиальной шины 175/70R13 (ширина 175 мм, отношение высоты к ширине 70%, посадочный диаметр 13 дюймов)

Задача 2.10.  

Радиус поворота автомобиля с эластичными шинами определяется по формуле:Rэ = L / tg q + tg (d₁ – d₂),

где d₁ и d₂ – углы увода шин переднего и заднего мостов (величины углов d₁, d₂, q обычно не велики).

Рис. 6

Схема движения автомобиля с нейтральной степенью поворачиваемости

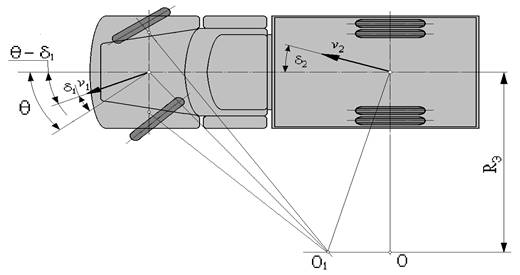на эластичных шинах:

d₁ и d₂ – углы увода шин переднего и заднего мостов; q - средний угол поворота; v₁ – вектор скорости переднего моста; v₂ – вектор скорости заднего моста; R_Э – радиус поворота с эластичными шинами.

Найти зависимость d₁ и d₂ для различных марок автомобилей по данным приложения №1

Рис. 7

Задача 2.11.  

Соотношение углов поворота управляемых колёс ctg q_Н = OC / L

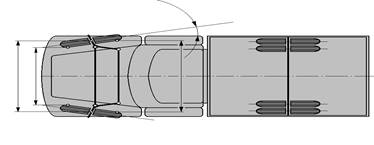ctg q_В = OA / L

Найти q_Н и q_В для разных марок автомобилей. Колесо внутренне по отношению к центру поворота должно быть повёрнуто на больший угол, чем внешнее, то есть q_В > q_Н (рулевая трапеция).

Задача 2.12.  

Определить, поднимется ли грузовик с данными на гору (высота горы), если максимальный угол подъёма

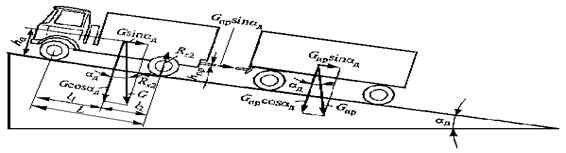tg a =  j_x G l₁ / (G (L – j_x h_a) + G_пр (L – j_x h_пр)),

где G_пр – вес прицепа; h_пр – высота расположения буксировочного крюка; G – вес автомобиля; j_x – коэффициент сцепления колёс дорогой.

Рис. 8

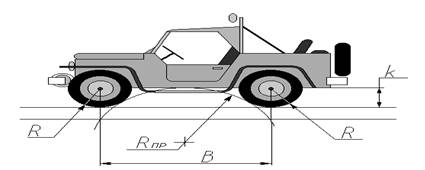Задача 2.13.  

Диаметр колеса (D) автомобиля составляет 600 мм. Автомобильная база (В) составляет 2000 мм. Клиренс (k) равен половине диаметра колеса. Необходимо определить допустимый радиус препятствия (Rпр), преодаливаемый автомобилем.

Решение: R = ½ D = ½ × 600 = 300 мм

k = ½ D = 300 мм

(Rпр + R)² = Rпр² + (B/2)² Þ Rпр = (B² – 4R²) / 8R

Rпр = (2000² – 4 ´ 300²) / 8 ´ 300 = 1516,6(6) мм.

Ответ: Допустимый радиус препятствия, преодаливаемый автомобилем, составляет 1516, 6(6) мм.

Задача 2.14. Рис.9

Геометрическая схема продольной проходимости автомобиля:

R_пр – радиус продольной проходимости, R_пооп – радиус поперечной проходимости,

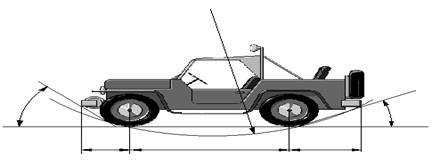 a – угол переднего свеса, b – угол заднего свеса, l_п – передний свес, l_з – задний свес,

 h – дорожный просвет.

Определить минимальный проходимый для автомобиля радиус канавы.

Задача 2.15.  

Если диаметр зубчатого колеса составляет 50 мм (см. рис.18а в приложении), а продольная тяга L имеет длину 200 мм, то на какой угол b относительно продольной оси автомобиля повернутся передние колёса, если рулевое колесо повернуть на Ða = 90° (рис.18 б)?

 

 

 

 

Функции и графики.

Задача 2.16.  

рис. 10

 

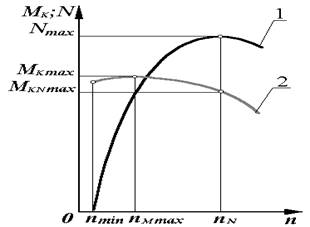Внешние скоростные характеристики двигателя

 без регулярной ветви.

По данным рисунка 20( в приложении) определить:

1.                                  Область определения функции;

2.                                  Множество значений функции;

3.                                  При каких значениях переменной функция:

1.                                                                                                          Положительная f(x) > 0;

2.                                                                                                          Отрицательная f(x) < 0;

3.                                                                                                          Равна нулю f(x) = 0 ?

4.                                  Промежутки монотонности функции.

5.                                  Точки экстремума.

6.                                  Наибольшее и наименьшее значение функции.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Заключение

 

Для технических профессий всегда необходимы задачи на движение, проценты, площади и объемы, составление уравнений и систем уравнений. Каждому человеку в своей жизни, в том числе и мне, приходится выполнять достаточно сложные расчеты, пользоваться вычислительной техникой, находить и применять нужные формулы, владеть приемами геометрических измерений, читать информацию, представленную в виде схем, таблиц, графиков и диаграмм.

В ходе работы над проектом я выяснил, что математические задачи можно составить и  найти в темах: коэффициент сопротивления качению, скорость и преодоление препятствий автомобилем, расход топлива, поворот колеса и другие.

Хочу отметить, что сам автомобиль сначала проектируется, рассчитываются многие показатели , например, мощность двигателя, выбирается материал  корпуса и деталей самой машины,изготовляется по чертежам, но об этом многие не задумываются, когда садятся за руль современного автомобиля.

В  результате работы над проектом я  :

·                                                развивал  познавательные  навыки  и умения:

·                                                самостоятельно конструировал свои знания ;

·                                                ориентировался  в информационном пространстве,

·                                                развивал творческое мышление;

·                                                раскрыл  значение науки – математика в жизни человека .

В ходе работы над проектом, проведя анализ,

· я выяснил: в каких областях автомобиля, в работе автомеханика  могут использоваться и понадобятся знания математики;

· я показал разнообразие профессиональных задач, решаемых математическими    методами;

· развить познавательные интересы, творческий коммуникативные способности определяющие формирование компетентной личности, способной к жизни деятельности, самоопределению в информационном обществе;

· научился правильно решать конкретные задачи, 

· самостоятельно добывать знания и их совершенствовать.

Считаю, что цели, поставленные перед выполнением проекта, выполнены. Я могу с твердой уверенностью  сделать  вывод о том, что «Математика» нужна не только в моей будущей профессии автомеханика - механика, математика нужна всем людям на земле.

Математики как дисциплина, развивает  интеллектуальные и творческие способности человека. Лучшего средства для их совершенствования еще не найдено.

Математика призвана ввести нас в таинственный и прекрасный мир. Хочу пожелать всем студентам, чтобы они научились не только извлекать пользу из занятий математикой, но и восхищаться ее красотой.

 

 

Литература

 

1.                       Шестаков С. К. Устройство легковых автомобилей : Учеб. М.: Академия,2016.

2.                      Пехальский А.П., Устройство автомобилей:М.: Академия, 2012.

3.                      Виноградов В. М. Технологические процессы ремонта автомобилей :М.: Академия,2012.

4.                      Власов В. М., Жанказиев С. В. Техническое  обслуживание и ремонт автомобилей:  М.: Академия,2011.

5.                       Акимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Шабунин М.И. Алгебра и начало анализа: Проб. Учеб. Для 10-11кл. сред. шк. М.: Просвещение, 1990.

6.                      Атаносян Л.С. Геометрия: Учеб. для 10-11 кл. сред. шк. М.: Просвещение, 1999.

7.                        Боровских Ю.И. и др. Устройство автомобилей: М.: Высшая школа, 1988.

8.                       Боровских Ю.И. Техническое обслуживание и ремонт автомобилей: М.: Высшая школа, 1988.

9.                      Вахламов В.К. и др. Автомобили: М.: Академия, 2003.

10.                 Вишняков Н.Н. и др. Автомобиль. Основы конструкции: М.: Академия, 1986.

11.                 Зорин В.В. Пособие по математике для поступающих в ВУЗы: М.: Высшая школа, 1980.

a.                      Иосилевич Г.Б. Детали машин: М.: Машиностроение, 1988.

12.                 Карагодин В.И., Митрохин Н.Н. Ремонт автомобилей и        двигателей: М.: Машиностроение, 2002.

13.                 Чумаченко Ю.Т. Автомобильный практикум: Ростов-на-Дону: Феникс, 2002.

 

 

Интернет ресурсы.

 

1.                      https://moluch.ru/archive/111/27588/ https://www.skachatreferat.ru/referaty/%D0%9C%D0%B0%D1%82%D0%B5https://thepresentation.ru/fizika/matematika-v-professii-avtomehanik

2.                      https://studfile.net/preview/5739639/page:2/

3.                      https://blog.autospot.ru/guide/tehobsluzhivanie

4.                      http://k-a-t.ru/PM.01_mdk.01.01/7_teoria_avto_upravl_2/index.shtml

Приложение

 

 

ТАБЛИЦА 1

Тип автомобиля	Минимальный радиус поворота, м	Минимальный внешний радиус, м	Минимальный внутренний радиус, м
Леговой автомобиль	6,55	6,85	4,42
Городской автобус	9,20	10,54	5,40
Пригородный автобус	11,07	11,82	6,15

Минимальный радиус поворота расчетных автомобилей

№ п/п	Покрытие дороги	Коэффициент сцепления  на сухой поверхности	Коэффициент сцепления  на мокрой поверхности
1	Асфальтобетонное	0,70 - 0,80	0,30 - 0,40
2	Щебенчатое	0,60 - 0,70	0,30 - 0,40
3	Булыжное	0,50 - 0,60	0,30 - 0,35
4	Грунтовые дороги	0,50 - 0,60	0,30 - 0,40
5	Глина	0,50 - 0,60	0,20 - 0,40
6	Песок	0,50 - 0,60	0,40 - 0,50
7	Уплотненный снег	0,20 - 0,30	-
8	Обледенелая дорога	0,08 - 0,10	-

 

ТАБЛИЦА 2

 

Индекс скорости	J	K	L	M	N	P	Q	R		S	T	U	H	V	VR	W	Y	ZR
Мах. Скорость (км/ч)	100	110	120	130	140	150	160	170	180		190	200	210	240	>210	270	300		>240

Таблица индексов скорости:

Таблица индексов нагрузки шины:

Индекс нагрузки	60	61	62	63	64	65	66	67	68	69
Мах. Нагрузка (в кг.)	250	257	265	272	280	290	300	307	315	325

 

Индекс нагрузки	70	71	72	73	74	75	76	77	78	79
Мах. Нагрузка (в кг.)	335	345	355	365	375	387	400	412	426	437

 

Индекс нагрузки	80	81	82	83	84	85	86	87	88	89
Мах. Нагрузка (в кг.)	450	462	475	487	500	515	530	545	560	580

 

Индекс нагрузки	90	91	92	93	94	95	96	97	98	99
Мах. Нагрузка (в кг.)	600	615	630	650	670	690	710	730	750	775

 

Индекс нагрузки	100	101	102	103	104	105	106	107	108	109
Мах. Нагрузка (в кг.)	800	825	850	875	900	925	950	975	1000	1030

 

Индекс нагрузки	110	111	112	113	114	115	116	117	118	119
Мах. Нагрузка (в кг.)	1060	1090	1120	1150	1180	1215	1250	1285	1320	1360

 

Индекс нагрузки	120	121	122	123	124	125	126	127	128	129
Мах. Нагрузка (в кг.)	1400	1450	1500	1550	1600	1650	1700	1750	1800	1850

 

 

Таблица 3

Значения коэффициента сопротивления качению

 

ТАБЛИЦА 4

Величины сил и коэффициентов трения некоторых марок автомобилей.

Марка	Ртр0	kтр
ВАЗ-2121	15	4
ГАЗ-53	80	2,75
КамАЗ-5320	102	11
МАЗ-6422	120	25

 

 

ТАБЛИЦА 5

 

 

 

 

 

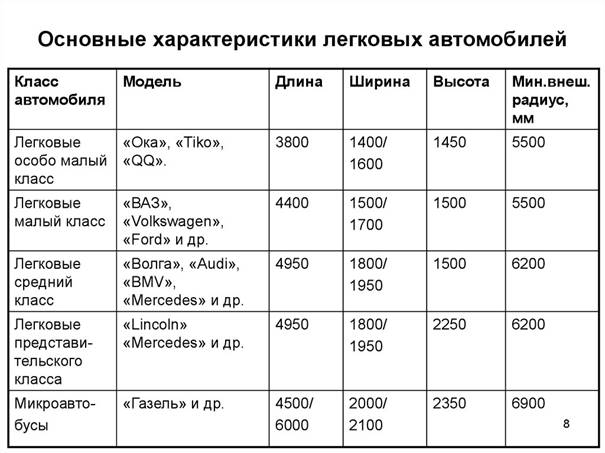
ТАБЛИЦА 6

Параметров сопротивления воздуха

Автомобиль	kЕ,  Hc2/м4	FЕ, м2
Легковые автомобили с кузовом: закрытым открытым	0,20...0,35 0,4...0,5	1,6...2,8 1,5...2,0
Грузовой автомобиль	0,6...0,7	3....5
Автобус с кузовом вагонного типа	0,24...0,40	4,5...6,0
Гоночный автомобиль	0,13...0,15	1,0...1,3

 

ТАБЛИЦА 7

 Применяемые шины для некоторых марок автомобилей приведены

№ п/п	Типоразмер шин	Марка автомобиля
1.	185/70R14	Ford
2.	195/65R15	Peugeot 307
3.	205/60R16	Peugeot 307 Audi A6
4.	215/55R17
5.	225/50R17
6.	225/55R16
7.	135/80R12	Ока – 2
8.	175/70R13
9.	175/60R14
10.

а)                                                                                      б)

РИСУНОК 18

Реечная схема управления поворотом колёс автомобиля:

1 – рулевое колесо; 2 – ось рулевой колонки; 3 – зубчатое колесо; 4 – зубчатая рейка;

5 – поперечная тяга; 6 – ось колеса; 7 – продольная тяга; 8 – колесо.

 

РИСУНОК  19

Рисунки протекторов шин (а...д)

и шины противоскольжения (е):

1 – сердечник; 2 – корпус.

 

 

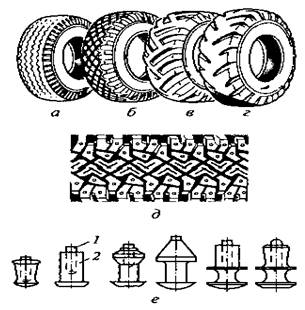
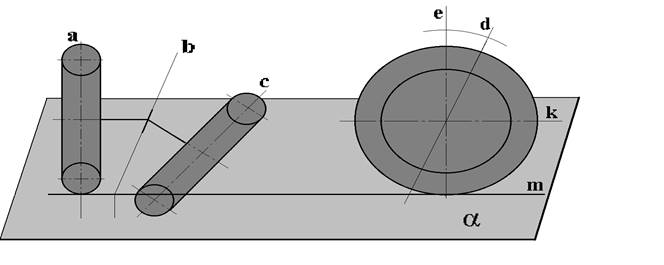
РИСУНОК 20

Схема установки шкворня.

 

 

РИСУНОК  21

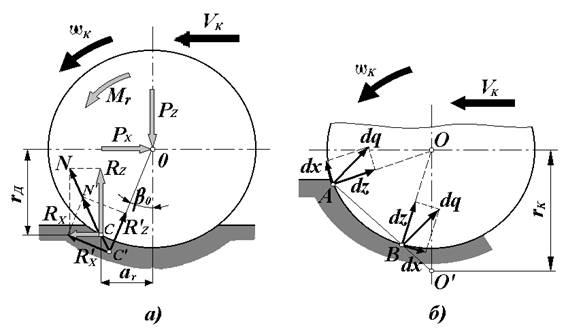Схема сил, действующих на колесо при качении

недеформируемого колеса по деформируемой дороге:

а – в ведущем режиме;

 б – распределение элементарных реакций в контакте.

 

 

 

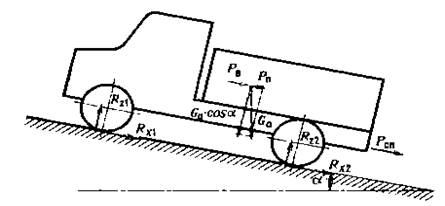
РИСУНОК 22

 

 

 

 

Схема сил, действующих на автомобиль во время торможения.

 

Определение максимального угла подъёма, преодолеваемого автопоездом:

 G – вес автомобиля; G_пр – вес прицепа; h_ц – высота расположения центра тяжести автомобиля; h_пр – высота расположения буксировочного крюка; L – база автомобиля.

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru