РЕКУРСИВНІ ФУНКЦІЇ ТА ПРОЦЕДУРИ

РЕКУРСИВНІ ФУНКЦІЇ ТА ПРОЦЕДУРИ

1.  Рекурсія. Рекурсивні функції. Рекурсіао називається алгоритмічна конструкція, де підпрограма викликає сама себе. Рекурсія дає змогу записувати циклічні алгоритми, не викорис­товуючи команди циклу. Розглянемо рекурсивні функції, але спочатку зупинимося на понятті стека.

Стек — це модель оперативної пам’яті (структура даних), де дані запам’ятовуються і зберігаються за принципом «перший прийшов — останнім пішов*. Аналогом у військовій справі є ріжок для набоїв до автомата.

Приклад 1. Рекурсивна функція обчислення суми цілих чисел від а до ft має вигляд

function Suma(a,b:integer):integer;

begin

if a =* b then Suma а {Це стоп-умова рекурсії} else Suma :- b + Suma(a, b-1) {Це неявний цикл}

end;

Обчислимо функцію Suma(3, 5). Формально можна записати Suma(3, 5) = 5 + Suma(3, 4) = 5 + 4 + Suma(3, 3) = 5 + 4 + 3. Система виконує такі обчислення за два етапи: 1) спочатку формує стек, куди заносить числа 5, 4, 3. На другому етапі чис­ла додає у зворотній послідовності (оскільки вони надходять зі стека): 3 + 4 + 5 = 12.

Приклад 2. Розглянемо рекурсивну функцію Factorial для обчислення факторіала числа л! = l-2-З-...-л, (0! = 1,1!= 1), яка грунтується на багаторазовому (рекурсивному) застосуванні формули п\ = п (п - 1)!.

function Factorial(n : integer): real;

begin

if n - 0 then Factorial :- 1 {Це стоп-умова} else Factorial :— n * Factorial(n - 1)

end;

Обчислимо 4!: Factorial(4) = 4 • Factorial(3) = 4 • 3 • Factorial(2)= = 4 • 3 • 2 • Factorial(l) = 4 • 3 • 2 • 1 • Factorial(O) = 4 • 3 • 2 • 1 • 1. У стек будуть занесені числа 4, 3, 2, 1, 1. Результат утвориться так: 1 • 1 • 2 • 3 • 4 = 24.

Зауваження. Застосовуючи рекурсію, потрібно правильно скла­дати стоп-умову, яка забезпечує закінчення циклу.

2.  Рекурсивні процедури. Задача про Ханойські вежі.

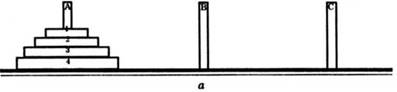
На рис. 14 зображено чотири диски на осі А. Потрібно переклас­ти диски на вісь С, користуючись віссю В так, щоб більший диск не класти на менший. За один раз можна перекладати один диск.

Складемо алгоритм і програму розв’язування задачі для п дисків. Спочатку розв’яжемо її для одного, двох, трьох і чотирьох дисків.

Нехай на осі А є один диск.

Алгоритм N6861^) (1, А, С, В) дає розв’язок задачі:

1.   Перекласти диск з осі А на вісь С.

Тепер нехай на осі А є два диски. Наступний алгоритм Ыеве- гао (2, А, С, В) дає розв’язок задачі:

1.  Перекласти диск 1 з осі А на вісь В.

2.  Перекласти диск 2 на вісь С.

3. Виконати алгоритм Nesemo (1, В, С, А), щоб перекласти диск з осі В на вісь С.

Нехай на осі А є три диски. Алгоритм Nesemo (З, А, С, В) дає розв’язок задачі:

1. Виконати алгоритм Nesemo (2, А, В, С), щоб перекласти два верхні диски з осі А на вісь В.

2.  Перекласти диск 3 на вісь С.

3. Виконати алгоритм Nesemo (2, В, С, А), щоб перекласти два диски з осі В на вісь С.

Нехай на осі А є чотири диски. Алгоритм Nesemo (4, А, С, В) дає розв’язок задачі:

1. Виконати алгоритм Nesemo (З, А, В, С), щоб перекласти три верхні диски з осі А на вісь В.

2.  Перекласти диск 4 на вісь С.

3. Виконати алгоритм Nesemo (З, В, С, А), щоб перекласти три диски з осі В на вісь С.

Нарешті розглянемо загальний випадок. Нехай на осі А єн дисків. Алгоритм Nesemo (n, А, С, В) дає розв’язок задачі:

1. Виконати алгоритм Nesemo (п-1, А, В, С), щоб перекласти л-1 верхні диски з осі А на вісь В.

2.  Перекласти диск п на вісь С.

3. Виконати алгоритм Nesemo (п-1, В, С, А), щоб перекласти л-1 диски з осі В на вісь С.

Алгоритм Nesemo (п. А, В, С) є рекурсивним. Справді, він двічі звертається сам до себе, але вже з іншими значеннями параметрів. Алгоритм для л дисків потребує виконання цього ж алгоритму для (л-1) диска, який відповідно потребує виконання цього ж алгоритму для (п-2) дисків,, а той потребує виконання цього алгоритму для двох дисків, який відповідно потребує виконання алгоритму для одного диска. Розгляньте програму.

program Hanoi; uses Crt; var n : integer;

{ Опис рекурсивної процедури Nesemo } procedure Nesemo (n : integer; А, С, В : char); begin

if n-1 then writeln ('Перекласти диск з осі

А," на вісь С)

else

begin

Nesemo (n - 1, А, В, С);

writeln ('Перекласти диск з осі А,

’ на вісь С);

Nesemo (n - 1, В, С, А) end

end; { кінець процедури Nesemo } begin clrscr; { початок основної програми }

writeln ('Задайте кількість дисків: '); readln (n); writeln (’Алгоритм для n, ' дисків такий:'); Nesemo (п, 'А', 'С', 'В') end. { кінець програми Hanoi }

Застосування рекурсивної процедури дало змогу складний алгоритм записати як компактну програму. Виконаємо програму Hanoi для трьох дисків. На екрані побачимо:

Задайте кількість дисків: З Алгоритм для 3 дисків такий:

Перекласти диск з осі А на вісь С Перекласти диск з осі А на вісь В Перекласти диск з осі С на вісь В Перекласти диск з осі А на вісь С Перекласти диск з осі В на вісь А Перекласти диск з осі В на вісь С Перекласти диск з осі А на вісь С

Виконайте програму Hanoi для чотирьох і п’яти дисків.

Запитання

1.  Що таке рекурсивна функція?

2.  Що таке рекурсивна процедура?

3.  Що таке стек?

4.  Для чого потрібна стоп-умова в рекурсії?

Вправи та задачі

1.  Запишіть головну програму обчислення факторіала, викорис­товуючи наведену в книжці рекурсивну функцію.

2.  Запишіть програму обчислення факторіала, використовуючи рекурсивну процедуру.

3.  Оформіть програму побудови таблиці для двох деяких мір на свій вибір як підпрограму-процедуру з параметром п — кількість рядків у таблиці. Перетворіть її на рекурсивну процедуру.

4.  Перетворіть деяку раніше складену програму з командою циклу в рекурсивну процедуру чи функцію.

5.  Скачано с www.znanio.ru