
Решение дробных рациональных уравнений
Цели: продолжить формирование умения решать дробные рациональные уравнения по алгоритму.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Найдите подбором корни уравнения:
а) х2 – 2х – 15 = 0; г) х2 – 29х + 100 = 0;
б) х2 + 5х + 6 = 0; д) х2 – 6х + 8 = 0;
в) х2 + 7х – 8 = 0; е) х2 + 15х + 36 = 0.
2. Решите уравнение:
а) 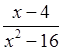 = 0; в)
= 0; в)
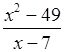 = 0;
= 0;
б) 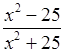 = 0; г)
= 0; г)
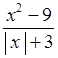 = 0.
= 0.
III. Формирование умений и навыков.
Упражнения, решаемые на этом уроке, направлены на закрепление умения решать дробные уравнения по алгоритму, а также некоторые представляют собой задания повышенной трудности.
1. № 608 (б, г), № 609 (а, б).
Р е ш е н и е
№ 608.
б) 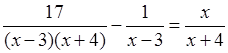 ; ОДЗ:
х ≠ 3; х ≠ –4.
; ОДЗ:
х ≠ 3; х ≠ –4.
17 – (х + 4) – х (х – 3);
17 – х – 4 – х2 + 3х = 0;
–х2 + 2х + 13 = 0.
D1 = 1 + 13 = 14, D1 > 0, 2 корня.
x1 = 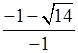 = 1 +
= 1 +
![]() ; x2
=
; x2
= 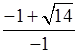 = 1 –
= 1 –
![]() .
.
г) 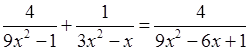 .
.
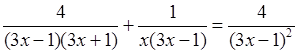 ; ОДЗ: x
≠
; ОДЗ: x
≠ ![]() ;
;
x
≠ –![]() .
.
Общий знаменатель дробей x(3x – 1)2(3x + 1).
4x(3x – 1) + (3x – 1)(3x + 1) = 4x(3x + 1);
12х2 – 4x + 9х2 – 1 = 12х2 + 4x;
9х2 – 8х – 1 = 0.
a + b + c = 0,
значит, x1 = 1, x2 = ![]() , то
есть x1 = 1, x2 =
, то
есть x1 = 1, x2 = ![]() .
.
О т в е т: б) 1 – ![]() ; 1 +
; 1 + ![]() ; г)
; г) ![]() ; 1.
; 1.
На этом примере наглядно демонстрируем учащимся необходимость разложения знаменателей на множители для последующего «составления» общего знаменателя.
№ 609.
а) 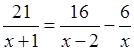 ; ОДЗ:
х ≠ –1; х ≠ 0; х ≠ 2.
; ОДЗ:
х ≠ –1; х ≠ 0; х ≠ 2.
21х(х – 2) = 16х(х + 1) – 6(х + 1)(х – 2);
21х2 – 42х = 16х2 + 16х – 6х2 + 6х + 12;
21х2 – 42х – 16х2 – 16х + 6х2 – 6х – 12 = 0;
11х2 – 64х – 12 = 0;
D1 = (32)2 – 11 · (–12) = 1024 + 132 = 1156; D1 > 0, 2 корня.
x1 = 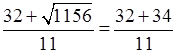 = 6;
= 6;
x2 = 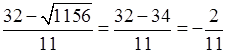 .
.
б) 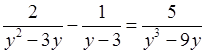 .
.
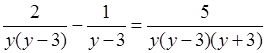 ; ОДЗ: у
≠ 0; у ≠ 3;
; ОДЗ: у
≠ 0; у ≠ 3;
у ≠ –3.
2(у + 3) – у(у + 3) – 5 = 0;
2у + 5 – у2 – 3у – 5 = 0;
–у2 – у = 0;
у2 + у = 0;
у (у + 1) = 0;
у = 0 или у = –1.
О т в е т: а) ![]() ; 6;
б) –1.
; 6;
б) –1.
2. 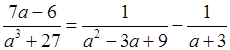 .
.
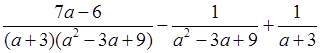 = 0; ОДЗ:
а ≠ –3.
= 0; ОДЗ:
а ≠ –3.
7а – 6 – (а + 3) + а2 – 3а + 9 = 0;
7а – 6 – а – 3 + а2 – 3а + 9 = 0;
а2 + 3а = 0;
а (а + 3) = 0;
а = 0 или а = –3.
О т в е т: 0.
3. 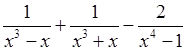 = 0.
= 0.
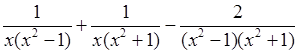 = 0.
= 0.
Общий знаменатель дробей х(х2 – 1)(х2 + 1).
Домножим обе части уравнения на общий знаменатель:
х2 + 1 + х2 – 1 – 2х = 0;
2х2 – 2х = 0;
2х (х – 1) = 0;
х = 0 или х = 1.
Если х = 0, то х(х2 – 1)(х2 + 1) = 0.
Если х = 1, то х(х2 – 1)(х2 + 1) = 0.
О т в е т: нет решений.
4. № 611 (б).
Р е ш е н и е
Графиком функции у = ![]() является
гипербола, расположенная в I и III координатных четвертях. Запишем координаты
контрольных точек:
является
гипербола, расположенная в I и III координатных четвертях. Запишем координаты
контрольных точек:
|
х |
0,5 |
1 |
2 |
3 |
6 |
|
у |
12 |
6 |
3 |
2 |
1 |
Графиком функции у = –х + 6 является прямая, проходящая через точки (0; 6), (6; 0).
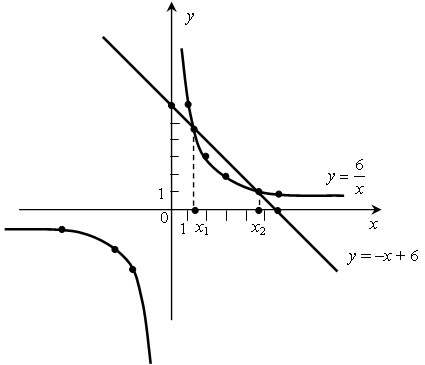
О т в е т: х1 ≈ 1,3; х2 ≈ 4,7.
5. Сильным в учебе учащимся можно предложить для решения задания повышенной трудности.
№ 610 (а), № 612.
Р е ш е н и е
№ 610.
а) 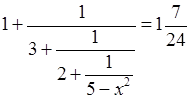 .
.
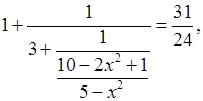
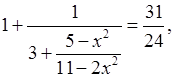
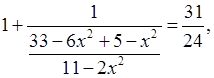
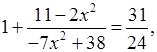
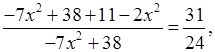
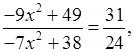
24(–9х2 + 49) = 31(–7х2 + 38),
–216х2 + 1176 + 217х2 – 1178 = 0,
х2 = 2,
х = ±![]() .
.
Оба корня удовлетворяют уравнению.
О т в е т: ±![]() .
.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие уравнения называются дробными рациональными?
– Каков алгоритм решения дробных уравнений?
– Как определить общий знаменатель дробей, входящих в уравнение?
– Каким способом можно исключить «посторонние» корни дробного рационального уравнения?
Домашнее задание: № 608 (а, в), № 609 (в), № 611 (а), № 695 (д, з).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.