РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ

Решение квадратных уравнений
с четным вторым коэффициентом

Цели: вывести формулу (II) нахождения корней квадратного уравнения с четным вторым коэффициентом; формировать умения применять формулы I и II для решения квадратных уравнений.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Назовите коэффициенты a, b, c уравнений:

а) 4х² – 5х – 7 = 0;                                 г) 8 – 9х² = 0;

б) х² + 2 – 3х = 0;                                   д) 11х² = 0;

в) 3х² + 2х = 0;                                       е) 17 – х² – х = 0.

2. Решите уравнение:

а) 2х² – 18 = 0;                                       в) х² + 16 = 0;

б) 3х² – 12х = 0;                         г) 3,6х² = 0.

3. Сколько корней имеет уравнение:

а) 6х² – 5х = 0;                                       в) 3х² – 4 = 0;

б) х² – 4х + 4 = 0;                                   г) 2х² + 7 = 0?

III. Объяснение нового материала.

 С о з д а н и е   п р о б л е м н о й   с и т у а ц и и.

Предложить учащимся для решения квадратное уравнение 15х² – 34х +
+ 15 = 0. Используя формулу нахождения корней квадратного уравнения, получаем:

D = (–34)² – 4 · 15 · 15 = 1156 – 900 = 256.

;

.

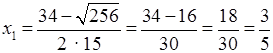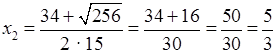Решая это уравнение, учащиеся вынуждены проводить вычисления достаточно громоздкие, в отличие от ранее решаемых уравнений.

Можно теперь сообщить учащимся, что для решения квадратных уравнений, у которых второй коэффициент четный, существует другая формула корней, позволяющая упростить вычисления.

Вывод этой формулы проводится согласно пункту учебника. Причём в сильном классе можно предложить учащимся проделать это самостоятельно, записав только общий вид такого уравнения:

ax² + 2 ∙  k ∙  x + c = 0     (b = 2k).

После вывода формулы возвращаемся к решенному уравнению и применяем новую формулу:

D = (–17)² – 15 · 15 = 289 – 225 = 64;

;

.

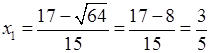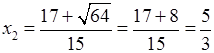Как видим, вычисления можно произвести «в уме», так как все значения квадратов чисел – табличные.

На доску можно вынести  п л а к а т:

(обращаем внимание учащихся, что D₁ в четыре раза меньше, чем D)

IV. Формирование умений и навыков.

Все  у п р а ж н е н и я, решаемые на этом уроке, можно разбить на три группы:

1-я  г р у п п а. Упражнения  на  непосредственное  применение  формулы (II) корней квадратного уравнения.

2-я  г р у п п а. Упражнения с выбором формулы (I или II) корней квадратного уравнения в зависимости от второго коэффициента.

3-я  г р у п п а. Упражнения повышенной трудности.

1. № 539 (б, г, ж), № 540 (в, з).

При решении этих упражнений демонстрируем учащимся применение новой формулы для случая, когда корни уравнения являются иррациональными. Для этого вызываем двух учеников к доске и параллельно проводим решение по разным формулам.

№ 539 (ж).

Р е ш е н и е

7z² – 20z + 14 = 0.

Таким образом, получаем такие же корни.

2. № 541 (б, в, ж), № 546 (а, г), № 550 (б), № 552 (а, в), № 553 (а).

3. № 554, № 555.

Эти упражнения можно предложить сильным в учебе учащимся, сократив для них количество заданий из 1-й и 2-й группы.

№ 554.

Р е ш е н и е

а) х² – 5х + 6 = 0;

D = (–5)² – 4 · 1 · 6 = 25 – 24 = 1, D > 0.

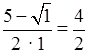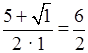x₁ =  = 2;                x₂ =  = 3.

6х² – 5х + 1 = 0;

D = (–5)² – 4 · 6 · 1 = 25 – 24 = 1, D > 0.

x₁ = 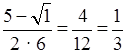; x₂ = .

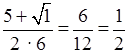б) 2х² – 13х + 6 = 0;

D = (–13)² – 4 · 2 · 6 = 169 – 48 = 121, D > 0.

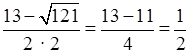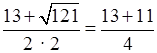x₁ = ;         x₂ =  = 6.

6х² – 13х + 2 = 0;

D = (–13)² – 4 · 6 · 2 = 169 – 48 = 121, D > 0.

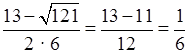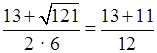x₁ = ;         x₂ =  = 2.

Можно  предположить,  что  корни  уравнений  ax² + bx + c = 0 и cx² +
+ bx + a = 0 являются взаимно-обратными числами. Докажем это.

(Мы предполагаем, что b² – 4ac ≥ 0, то есть корни существуют.)

Вычислим  x₁ ∙  x₄ = =

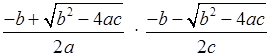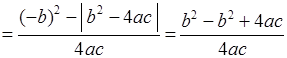 = 1. Значит, х₁ и х₄ – взаимно-обратные числа.

Аналогично доказывается, что x₂ и x₃ – взаимно-обратные числа.

№ 555.

Р е ш е н и е

х² – ах + (а – 4) = 0.

D = (–а)² – 4 · 1 · (а – 4) = а² – 4а + 16.

Чтобы определить количество корней, необходимо оценить дискриминант. Выделим в выражении квадрат двучлена:

D = (а² – 2 · 2 · а + 4) + 12 = (а – 2)² + 12.

Дискриминант принимает положительные значения при любом а (точнее D ≥ 12), значит, при любом а уравнение имеет два корня.

О т в е т: а) нет; б) нет; в) при любом а.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– В каких случаях применяется формула II корней квадратного уравнения?

– В каком отношении находятся D₁ и D?

– По какой формуле вычисляется D₁?

– Можно ли применять формулу I корней квадратного уравнения, если коэффициент b чётный?

– Могут ли получиться разные корни при применении различных формул корней квадратного уравнения?

Домашнее задание: № 539 (в, е, з), № 540 (б, е, ж), № 541 (е, з), № 548 (б, г), № 551 (а, г, д).