РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ

Решение неполных квадратных уравнений

Цели: формировать умения решать неполные квадратные уравнения различных видов.

Ход урока

I. Организационный момент.

II. Устная работа.

– Найдите корни уравнения:

а) х² = 0;           б) х² = 16;           в) х² = ;           г) х² = 144;

д) х² = ;          е) х² = ;          ж) х² = 2,56;          з) х² = .

III. Проверочная работа.

В а р и а н т  1

Составить квадратное уравнение по его коэффициентам и проверить, является ли указанное число х₀ корнем этого уравнения:

а) a = 2; b = –3; c = 1; х₀ = ;

б) a = –1; b = 4; c = 0; х₀ = 4;

в) a =; b = –1; c =; х₀ =.

В а р и а н т  2

Составить квадратное уравнение по его коэффициентам и проверить, является ли указанное число х₀ корнем этого уравнения:

а) a = 3; b = –2; c = –1; х₀ = ;

б) a = –1; b = 0; c = 9; х₀ = 3;

в) a =; b = –1; c =; х₀ =.

IV. Объяснение нового материала.

Для осознанного восприятия приёмов решения неполных квадратных уравнений объяснение проводим на конкретных примерах с последующим составлением алгоритмов решения.

1. № 514 (устно).

2.

П р и м е р  1. 3,8х² = 0.

Р е ш е н и е

– Разделим обе части уравнения на 3,8 (число, не равное нулю) и получим уравнение, равносильное исходному:

х² = 0.

Мы знаем, что существует только одно число – нуль, квадрат которого равен нулю, следовательно, уравнение имеет единственный корень х₀ = 0.

О т в е т: 0.

В ы в о д:  уравнение  вида  ах² = 0  (а ≠ 0)  имеет  единственный  корень х₀ = 0.

3.

П р и м е р  2. –3х² + 21 = 0.

Р е ш е н и е

– Перенесём свободный член в правую часть уравнения и разделим обе части получившегося уравнения на –3:

–3х² = –21;

х² = 7.

Отсюда х =  или х = –.

О т в е т: х = ; х = –.

П р и м е р  3. 4х² + 6 = 0.

Р е ш е н и е

– Перенесём свободный член в правую часть уравнения и разделим обе части получившегося уравнения на 4:

4х² = –6;

х² = .

Так как квадрат числа не может быть отрицательным числом, то уравнение не имеет корней.

О т в е т: нет корней.

В ы в о д: для решения уравнения вида ах² + с = 0 (с ≠ 0) воспользуемся алгоритмом:

1) Перенесём свободный член с в правую часть уравнения.

2) Делим  обе  части  уравнения  на  а  (с ≠ 0, а ≠ 0),  получаем  уравнение х² = .

3) Если  > 0, то уравнение имеет два корня:

.

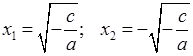Если  < 0, то уравнение не имеет корней.

4.

П р и м е р  4. 5х² + 7х = 0.

Р е ш е н и е

– Разложим левую часть уравнения на множители:

х (5х + 7) = 0.

Отсюда: х = 0   или       5х + 7 = 0;

                                         5х = –7;

                                         х = ;

                                         х = –1,4.

О т в е т: 0; –1,4.

В ы в о д: для решения уравнения вида ах² + bx = 0 (b ≠ 0) воспользуемся алгоритмом:

1) Разложим  левую  часть  уравнения  на  множители,  получим x (ax +
+ b) = 0.

2) Решаем уравнение ах + b = 0; х = .

3) Уравнение имеет два корня: .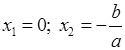

5. Приведённые примеры показывают учащимся, что неполное квадратное уравнение может иметь один или два корня, а может и не иметь корней. В дальнейшем возможно обобщение этого вывода для любых квадратных уравнений.

Для систематизации знаний, полученных на уроке, можно предложить учащимся составить следующую таблицу:

V. Формирование умений и навыков.

На первых порах желательно, чтобы учащиеся перед решением неполных квадратных уравнений вслух проговаривали их вид и алгоритм решения, пока не будет сформирован устойчивый навык.

№ 515 (а, в, д), № 517 (а, в, е), № 519 (устно), № 523 (а, в).

VI. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Какое квадратное уравнение называется неполным?

– Какие существуют виды неполных квадратных уравнений?

– Какие корни имеет уравнение вида ах² = 0?

– Как решается неполное квадратное уравнение, в котором коэффициенты b = 0, с ≠ 0? Сколько корней может иметь такое уравнение?

– Как решается неполное квадратное уравнение, в котором коэффициенты b ≠ 0, с = 0? Сколько корней может иметь такое уравнение?

Домашнее  задание:  № 515  (б, г, е),  № 518  (а, г, д, е),  № 521  (а, в), № 520, № 522 (а, в).