
Решение неравенств, содержащих дроби
Цели: разобрать способ решения неравенств с одной переменной, содержащих дроби; продолжить формирование навыков решения неравенств путём перехода к равносильным неравенствам.
Ход урока
I. Организационный момент.
II. Математический диктант.
В а р и а н т 1 [В а р и а н т 2]
1. Запишите числовой промежуток, служащий множеством решений неравенства х ≤ 3 [y > –8].
2. Запишите неравенство, множеством решений которого служит промежуток (–3; +∞) [(–∞; 7)].
3. Решите неравенство:
2х – 1 ≤ 2(2х – 3) [3(2х + 1) ≥ 3х + 1].
4. Решите неравенство:
5(а2 – 1) – 5а(а + 2) > 3 [6х2 – 3х(2х + 4) > 48].
О т в е т ы:
|
|
В а р и а н т 1 |
В а р и а н т 2 |
|
1 |
(–∞; 3] |
(–8; +∞) |
|
2 |
х > –3 |
х < 7 |
|
3 |
|
|
|
4 |
(–∞; –0,8) |
(–∞; –4) |
III. Объяснение нового материала.
Проверить из домашнего задания № 871 (а).
Рассмотреть по учебнику пример 3 на с. 178.
IV. Формирование умений и навыков.
В предлагаемых заданиях необходимо уметь находить общий знаменатель дробей, входящих в запись уравнения, затем домножить обе части неравенства на общий знаменатель и решить полученное неравенство. Также следует уделять внимание изображению множества решений на координатной прямой.
1. № 849 (а, д, ж, з, и).
Р е ш е н и е
а) ![]() >
1;
>
1; ![]() ∙
5 > 1 ∙ 5; 2x > 5; x > 5 : 2; x
> 2,5.
∙
5 > 1 ∙ 5; 2x > 5; x > 5 : 2; x
> 2,5.
д) 2 > ![]() ;
2 ∙ 5 >
;
2 ∙ 5 > ![]() ∙ 5; 10 > 6 – x;
x > 6 – 10; x > –4.
∙ 5; 10 > 6 – x;
x > 6 – 10; x > –4.
ж) 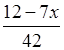 ≥
0;
≥
0; 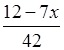 ∙
42 ≥ 0 ∙ 42; 12 – 7x ≥ 0; –7x ≥
–12;
∙
42 ≥ 0 ∙ 42; 12 – 7x ≥ 0; –7x ≥
–12;
х ≤ (–12) : (–7); х
≤ 1![]() .
.
з) ![]() (х
+ 15) > 4;
(х
+ 15) > 4; ![]() (х + 15) ∙ 3
> 4 ∙ 3; х + 15 > 12; x > 12 – 15;
(х + 15) ∙ 3
> 4 ∙ 3; х + 15 > 12; x > 12 – 15;
х > – 3.
и) 6 ≤ ![]() (х
+ 4); 6 ∙ 7 ≤
(х
+ 4); 6 ∙ 7 ≤ ![]() (х + 4) ∙ 7;
42 ≤ 2х + 8; –2x ≤ 8 – 42;
(х + 4) ∙ 7;
42 ≤ 2х + 8; –2x ≤ 8 – 42;
–2x ≤ –34; х ≥ 17.
О т в е т: а) х > 2,5; д) х
> –4; ж) х ≤ 1![]() ; з) х > –3; и) х
≥ 17.
; з) х > –3; и) х
≥ 17.
№ 851 (а, в).
Р е ш е н и е
|
а) 2(7 – 2у) > 3у – 7; 14 – 4у > 3у – 7; –4у – 3у > –14 – 7; –7у > –21; у < (–21) : (–7); у < 3. |
б) 5y
– 1 > 4(5y – 1) > 3y – 1; 20y – 4 > 3y – 1; 20y – 3y > 4 – 1; 17y > 3; y
> |
О т в е т: а) при у < 3; в) при y
> ![]() .
.
2. № 852 (б, г, е).
Р е ш е н и е
|
а) 3 ∙ 3y – 2y ≥ 2 ∙ 6; 9y – 2y ≥ 12; 7y ≥ 12; y ≥ 12 : 7; y ≥ 1 |
б) y + 2y + y > 6; 3y > 6; y > 2. (2; +∞). |
е) 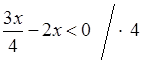 ;
;
3х – 8х < 0;
–5х < 0;
х > 0 : (–5);
х > 0. (0; +∞).
О т в е т: б) 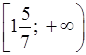 ; г)
(2; +∞); е) (0; +∞).
; г)
(2; +∞); е) (0; +∞).
№ 853 (б, г).
Р е ш е н и е
б) 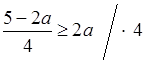 ;
;
5 – 2а ≥ 8а;
–2а – 8а ≥ –5;
|
–10а ≥ –5; а ≤ (–5) : (–10); а ≤ |
|
г) 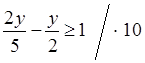 ;
;
|
2 · 2у – 5у ≥ 10; –у ≥ 10; у ≤ –10. (–∞; –10]. |
|
О т в е т: б) 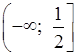 ; г)
(–∞; –10].
; г)
(–∞; –10].
3. № 854.
Р е ш е н и е
а) 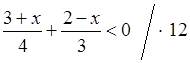 ;
;
3(3 + х) +4(2 – х) < 12 · 0;
9 + 3х + 8 – 4х < 0;
|
3х – 4х < –9 – 8; –х < –17; х > 17. (17; +∞). |
|
б) 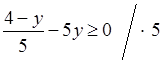 ;
;
4 – у – 25у ≥ 0;
|
–26у ≥ –4; у ≤ (–4) : (–26); у ≤ |
|
в) 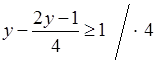 ;
;
4у – 2у + 1 ≥ 4;
|
2у ≥ 3; у ≥ 3 : 2; у ≥ 1,5. [1,5; +∞). |
|
г) 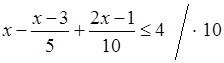 ;
;
10х – 2(х – 3) + 2х – 1 ≤ 40;
10х – 2х + 6 + 2х – 1 ≤ 40;
10х ≤ –6 + 1 + 40;
|
10х ≤ 35; х ≤ 35 : 10; х ≤ 3,5. (–∞; 3,5]. |
|
д) 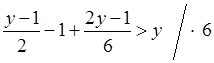 ;
;
3(у – 1) – 6 + 2у – 1 > 6у;
3у – 3 – 6 + 2у – 1 > 6у;
|
5у – 6у > 10; –у > 10; у < 10. (–∞; –10). |
|
е) 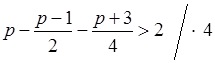 ;
;
4р – 2(р – 1) – р – 3 > 8;
|
4р – 2р + 2 – р – 3 > 8; р > 8 + 1; р > 9. (9; +∞). |
|
О т в е т: а) (17; +∞); б) 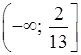 ; в)
[1,5; +∞); г) (–∞; 3,5]; д) (–∞; –10); е) (9; +∞).
; в)
[1,5; +∞); г) (–∞; 3,5]; д) (–∞; –10); е) (9; +∞).
№ 856 (б).
Р е ш е н и е
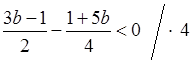
2(3b – 1) – 1 – 5b < 0;
6b – 2 – 1 – 5b < 0;
b < 3.
О т в е т: при b < 3.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что значит «решить неравенство с одной переменной»?
– Каков алгоритм решения неравенства с одной переменной, содержащего дробь?
Домашнее задание: №
850, № 851 (б, г), № 852 (а, в, д), № 855,
№ 856 (а).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.