
Решение
неравенств вида 0 · х > b или 0 · х < b,
где b – некоторое число
Цели: рассмотреть решение неравенств, которые либо не имеют решений, либо их решением является любое число; продолжить формировать умения решать неравенства с одной переменной, а также задачи, сводящиеся к решению таких неравенств.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
1. Решите неравенство:
а) ![]() – x
> 3; б)
– x
> 3; б) 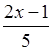 – 2x
>
– 2x
> 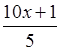 .
.
2. При каких значениях b двучлен 2b + 11 принимает положительные значения?
В а р и а н т 2
1. Решите неравенство:
а) ![]() – x
> 2; б)
– x
> 2; б) 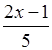 – 3x
>
– 3x
> 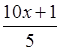 .
.
2. При каких значениях а двучлен 12 – а принимает положительные значения?
О т в е т:
|
|
В а р и а н т 1 |
В а р и а н т 2 |
|
1 |
а)
(–∞; –5); б) |
а)
(–∞; –8); б) |
|
2 |
(–5,5; +∞) |
(–∞; 12) |
III. Устная работа.
1. Решить неравенство:
а) 2х + 1 > 5; б)
–3х + 9 ≤ 0; в) ![]() <
0;
<
0;
г) ![]() ≥
0; д)
≥
0; д) 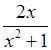 ≤ 0; е)
≤ 0; е)
![]() <
0.
<
0.
2. Какие из чисел 0; 7; –4; 6; ![]() являются
решением неравенства
являются
решением неравенства
3х – 12 ≥ 6?
IV. Объяснение нового материала.
1. С о з д а н и е п р о б л е м н о й с и т у а ц и и.
На предыдущих уроках мы решали неравенства вида ах > b (ax < b), где а ≠ 0. Алгоритм решения был прост: мы преобразовывали неравенства к такому виду, а затем делили обе части неравенства на коэффициент а (с учетом знака) и получали числовой промежуток в качестве решения. Пробуем применить этот алгоритм к следующему упражнению:
2(х + 8) – 5х < 4 – 3х;
2х + 16 – 5х < 4 – 3х;
2х – 5х + 3х < –16 + 4;
0 · х < –12.
Наш алгоритм «не работает» – на нуль делить нельзя. Замечаем, что неравенство будет иметь решение, если при подстановке какого-то числа вместо х мы получим верное неравенство. Но в данном случае при любом значении х неравенство обращается в числовое 0 < –12, которое является неверным, значит, исходное неравенство не имеет решений.
2. Решить самостоятельно упражнение:
5(х + 11) – 9х < 65 – 4х;
5х + 55 – 9х < 65 – 4х;
5х – 9х + 4х < 65 – 55;
0 · х < 10.
Замечаем, что при любом значении х неравенство обращается в верное числовое неравенство 0 < 10, значит, решением является любое число.
3. Делаем общий в ы в о д: неравенства
вида 0 · х > b (0 · x < b), а значит, и
неравенства, равносильные данным, либо не имеют решений, либо их
решением является любое число (множество решений либо ![]() , либо
(–∞; +∞)).
, либо
(–∞; +∞)).
V. Формирование умений и навыков.
Упражнения, решаемые на этом уроке, можно разбить на 3 г р у п п ы:
1) Решение неравенств, сводящихся к
неравенствам вида 0 · х > b
(0 · x < b).
2) Решение задач, сводящихся к решению неравенств с одной переменной.
3) Решение заданий повышенной трудности.
1. № 857 (а, б).
Р е ш е н и е
а) 31(2х + 1) – 12х > 50х;
62х + 31 – 12х > 50х;
62х – 12х – 50х > –31;
0 · х > –31;
при любом значении х имеем верное неравенство 0 > –31, значит, х – любое число.
б) х + 4 – 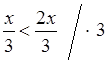 ;
;
3х + 12 – х < 2х;
3х – х – 2х < –12;
0 · х < –12;
при любом значении х имеем неверное неравенство 0 < –12, значит, неравенство не имеет решений.
О т в е т: а) х – любое число; б) нет решений.
№ 858.
Р е ш е н и е
у > 0, если 2х + 13 > 0; 2х > –13; х > –6,5;
у < 0, если 2х + 13 < 0; 2х < –13; х < –6,5.
О т в е т: (–6,5; +∞); (–∞; –6,5).
№ 859 (а, в, д).
Р е ш е н и е
а) При 2х – 4 ≥ 0; 2х ≥ 4; х ≥ 2.
в) При 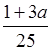 ≥
0; 1 + 3a ≥ 0; 3a ≥ –1; a ≥
≥
0; 1 + 3a ≥ 0; 3a ≥ –1; a ≥ ![]() .
.
д) При –3(1 – 5х) ≥ 0; 1 – 5х ≤ 0; –5х ≤ –1; х ≥ (–1) : (–5); х ≥ 0,2.
О т в е т: а) при х ≥ 2; в)
при a ≥ ![]() ; д) при х ≥ 0,2.
; д) при х ≥ 0,2.
2. № 861 (а).
Р е ш е н и е
1,6 – (3 – 2у) < 5;
1,6 – 3 + 2у < 5;
|
2у < 5 – 1,6 + 3; 2у < 6,4; у < 3,2. (–∞; 3,2). |
|
Наибольшее целое число, удовлетворяющее неравенству, равно 3.
О т в е т: 3.
№ 862 (а).
Р е ш е н и е
(2 – 2п) – (5п – 27) > 0;
2 – 2п – 5п + 27 > 0;
|
–7п > –29; п < (–29) : (–7); п < 4 |
|
Данному неравенству удовлетворяют натуральные числа 1, 2, 3, 4.
О т в е т: 1; 2; 3; 4.
3. № 865.
Р е ш е н и е
Пусть х см – длина другой стороны прямоугольника, тогда его периметр равен 2 · (х + 6) см; периметр квадрата равен 4 · 4 см, то есть 16 см. Зная, что периметр прямоугольника меньше периметра квадрата, составим неравенство:
2(х + 6) < 16;
2х + 12 < 16;
2х < 4;
х < 2.
О т в е т: меньше 2 см.
4. Сильным в учебе учащимся можно предложить для решения задания повышенной трудности.
№ 860 (а), № 863, № 869.
Р е ш е н и е
№ 860 (а).
В область определения функции y = 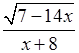 входят
значения х, для которых 7 – 14х ≥ 0 и х + 8 ≠
0.
входят
значения х, для которых 7 – 14х ≥ 0 и х + 8 ≠
0.
7 – 14х ≥ 0; х + 8 ≠ 0;
|
–14х ≥ –7,; х ≠ –8. х ≤ (–7) : (–14); х ≤ 0,5. |
|
О т в е т: (–∞; –8) ![]() (–8;
0,5].
(–8;
0,5].
П р и м е ч а н и е. На этом примере учащиеся видят, что если в решении в полученном числовом промежутке есть «выколотая» точка, то ответ мы записываем в виде объединения числовых промежутков.
№ 863.
(а + 5)х2 + 4х – 20 = 0 – квадратное уравнение
D1 = 4 – (а + 5) · (–20) = 4 + 20а + 100 = 20а + 104.
Уравнение не имеет корней, если D1 < 0, то есть:
20а + 104 < 0;
20а < –104;
а < (–104) : 20;
а < –5,2.
О т в е т: при а < –5,2.
П р и м е ч а н и е. Необходимо сообщить учащимся, что данное уравнение представляет собой уравнение с параметром а и переменной х.
№ 869.
Р е ш е н и е
А н а л и з
|
|
|
Vсоб = 18 км/ч Vтеч = 2 км/ч |
|
V1 = Vсоб + Vтеч
|
|
|
|
|
|
|
|
х км |
V2 = Vсоб – Vтеч |
|
Пусть х км – расстояние, на
которое могут отъехать туристы, тогда по течению они плыли со скоростью 18
+ 2, то есть 20 км/ч, и против течения – со скоростью 18 – 2, то есть 16 км/ч,
и на путь по течению они затратили ![]() ч, а
против течения
ч, а
против течения ![]() ч. Зная, что туристы должны
вернуться к стоянке не позднее, чем через 3 часа, составим неравенство:
ч. Зная, что туристы должны
вернуться к стоянке не позднее, чем через 3 часа, составим неравенство:
![]() +
+ ![]() ≤
3
≤
3 ;
;
4х + 5х ≤ 240;
9х ≤ 240;
х ≤ 26![]() .
.
О т в е т: не более 26![]() км.
км.
VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Сколько решений может иметь неравенство с одной переменной?
– В каком случае неравенство не имеет решений? Приведите примеры.
– В каком случае решением неравенства является любое число? Приведите примеры.
Домашнее задание: № 857 (в, г), № 859 (б, г, е), № 861 (б), № 862 (б), № 866, № 867*.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.