Решение тригонометрических уравнений разложением на множители. (Профильный уровень).

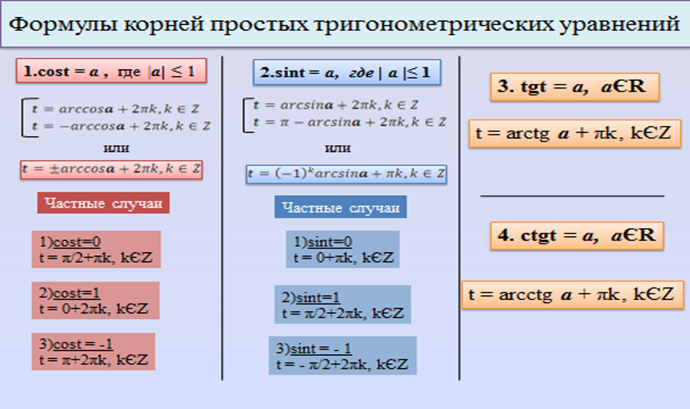
Тригонометрические уравнения из материалов ЕГЭ профильного уровня.

Часть 2.

Разложение на множители.

Справочный материал.

 

 

 

 

 

 

 

 

 

1. а)   уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Преобразуем уравнение:

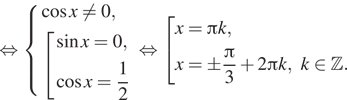
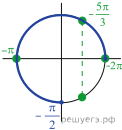
б)  Отберем корни на промежутке с помощью тригонометрической окружности. Получаем и

 

Ответ: а) б)

Критерии проверки:

Ответ: а) б)

507886

а) б)

Классификатор алгебры: Уравнения, рациональные относительно тригонометрических функций

Методы алгебры: Формулы приведения

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения

2.     а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решени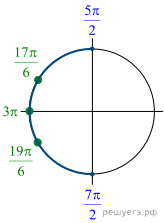е. а)  Запишем уравнение в виде

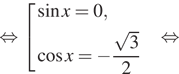
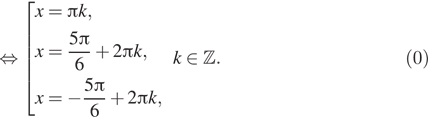
б)  С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:

Ответ: а) б)

Критерии проверки:

Ответ: а) б)

500111

а) б)

Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители

Методы алгебры: Формулы двойного угла

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения

3.      а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Используем формулу синуса двойного угла, выносим за скобки:

 

 

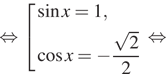
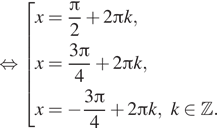
б)  Изображая корни на единичной окружности, находим, что отрезку принадлежат корни и

 

Ответ:а) б)

Критерии проверки:

Ответ: а) б)

509501

а) б)

Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад.

Классификатор алгебры: Тригонометрические уравнения

Методы алгебры: Формулы двойного угла

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения

4. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие промежутку

Решение. а)  Перенесём все члены в левую часть, преобразуем и разложим левую часть на множители:

1 случай. Если то

2 случай. Если то При решений нет. Разделим обе части уравнения на Получаем

Тогда

б)  Отрезку принадлежат корни и

 Ответ: а) б) и

5. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Преобразуем уравнение:

 

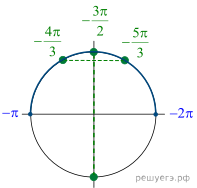
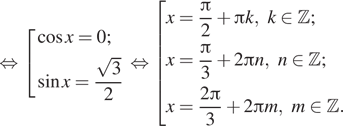
б)  С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа

 Ответ: а) ) б)

6. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  В силу нечетности и периодичности синуса имеем:

Далее имеем:

 

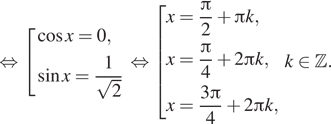
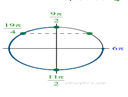
б)  При помощи числовой прямой или тригонометрической окружности (см. рис.) для каждой из задающих решения серий отберем корни уравнения, принадлежащие отрезку

Находим три решения:

 Ответ: а)   б)  

7. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие промежутку

Решение. а)  Так как и имеем:

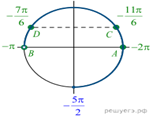
Корни уравнения:

б)  Корни уравнения изображаются точками A и B, а корни уравнения   — точками C и D, промежуток изображается жирной дугой (см. рис.). В указанном промежутке содержатся три корня уравнения: и

 

Ответ:а) б)

Критерии проверки:

Ответ: а) б)

500815

а) б)

Источник: Демонстрационная версия ЕГЭ—2013 по математике.

Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители

Методы алгебры: Формулы двойного угла, Формулы приведения

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения

8.   а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

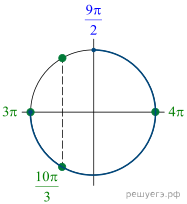Решение. а)  Преобразуем уравнение : Получаем или откуда или где

б)  На отрезке корни отберем с помощью единичной окружности. Получаем и

Ответ: а) б)

9. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. Решим уравнение:

 

 

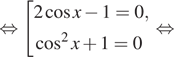
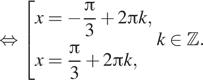
б)  Укажем корни этого уравнения, принадлежащие отрезку Получим точку

 

Ответ: а) б)

10. а)  Решите уравнение

 б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Имеем:

 

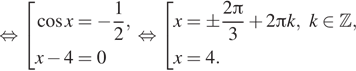
б) 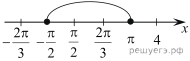  При помощи числовой оси отберем корни, принадлежащие отрезку получим число

 Ответ: а) б)

11. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Преобразуем уравнение:

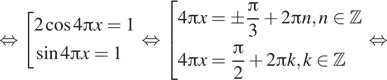
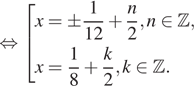
б)  Ограничим каждое полученное решение из пункта «а» и решим эти неравенства:

1)  

 

2)

3)

Ответ: а) б)

12. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие промежутку

Решение. 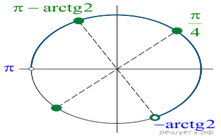а)  Решим уравнение:

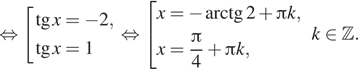
б)  Отберём корни при помощи тригонометрической окружности. Заданному условию удовлетворяют корни и

Ответ: а) б)

13. а)  Решите уравнение

б)  Найдите все его корни этого уравнения, принадлежащие отрезку

Решение. а)  Запишем исходное уравнение в виде:

Следовательно, или а значит, или

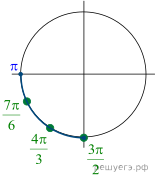
б)  Корни, принадлежащие промежутку отберём с помощью

единичной окружности. Получаем:

 

Ответ: а) б)

Критерии проверки:

Ответ: а) б)

560137

а) б)

Классификатор алгебры: Сравнение чисел, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители, Тригонометрические формулы суммы или разности аргументов

Методы алгебры: Тригонометрические формулы суммы и разности аргументов

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения

14.    а)  Решите уравнение б)  Найдите все корни этого уравнения, принадлежащие отрезку

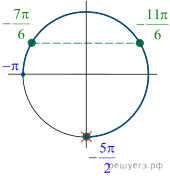Решение. а)  Запишем исходное уравнение в виде:

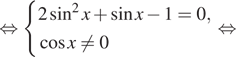
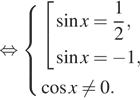
Корни уравнения не удовлетворяют условию Тогда получаем:

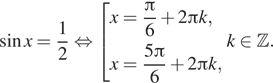
б)  Отберём корни, принадлежащие промежутку с помощью единичной окружности. Получаем

 

Ответ: а) б)

 

 

 

 

 

 

 

Решить самостоятельно.

1. а)  Решите уравнение б)  Укажите корни уравнения, принадлежащие отрезку 2. а)  Решите уравнение б)  Найдите все корни этого уравнения, при  надлежащие промежутку

3. а)  Решите уравнение   б)  Найдите все корни этого уравнения, принадлежащие отрезку

4. а)  Решите уравнение   б)  Укажите корни этого уравнения, принадлежащие отрезку

5. а)  Решите уравнение 

б)  Укажите корни этого уравнения, принадлежащие отрезку

6. а)  Решите уравнение б)  Найдите все корни этого уравнения, принадлежащие промежутку

7. а)  Решите уравнение:  б)  Определите, какие из его корней принадлежат отрезку

8. а)  Решите уравнение  б)  Найдите все его корни, принадлежащие отрезку

9. а)  Решите уравнение     б)  Найдите все его корни, принадлежащие отрезку

10. а   )  Решите уравнение

б)  Найдите все корни уравнения, принадлежащие отрезку

 

Ответы.

1. а) б)   

2. а) б)   

3. а) б)   

4. а) б)

5. а) б)   

6. а) б)    

7. а) б)  

8. а) б)    

9. а) б)    

10. а) б) 0,

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru