Решение уравнений

1. (Устно.) Решите уравнения:

Пример 1. Решите уравнение  

Решение. 

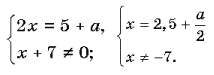
Найдем недопустимые значения a: 

Ответ. Если  если a = – 19, то корней нет.

Пример 2. Решите уравнение 

Решение. 

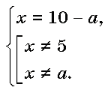
Найдем недопустимые значения параметра a:

10 – a = 5, a = 5;

10 – a = a, a = 5.

Ответ. Если a = 5, то уравнение теряет смысл; если a¹5, то x=10–a.

Пример 3. При каких значениях параметра b уравнение  имеет:

а) два корня; б) единственный корень?

Решение. 

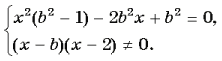
1) Найдем недопустимые значения параметра b:

x = b, b²(b² – 1) – 2b³ + b² = 0,  b⁴ – 2b³ = 0, 
b = 0 или b = 2;
x = 2, 4(b² – 1) – 4b² + b² = 0, b² – 4 = 0, (b – 2)(b + 2) = 0,
b = 2 или b = – 2.

2) Решим уравнение x²(b² – 1) – 2b²x + b² = 0:

D = 4b⁴ – 4b²(b² – 1),   D = 4b².

а)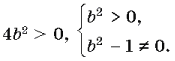  

Исключая недопустимые значения параметра b, получаем, что уравнение имеет два корня, если b¹– 2, b¹– 1, b¹0, b¹1, b¹2.

б) 4b² = 0, b = 0,  но это недопустимое значение параметра b; если b²–1=0, т. е. b=1 или.

Ответ: а) если b¹–2, b¹–1, b¹0, b¹1, b¹2, то два корня; б) если b=1 или b=–1, то единственный корень.

Самостоятельная работа

Вариант 1

Решите уравнения:

Вариант 2

Решите уравнения:

Ответы

В-1. а) Если a=3, то корней нет; если  б) если  если a¹2, то корней нет.

В-2. Если a=2, то корней нет; если a=0, то корней нет; если 
б) если a=– 1, то уравнение теряет смысл; если то корней нет; 
если 

Задание на дом.

Решите уравнения:

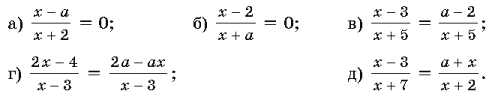
Ответы: а) Если a¹–2, то x=a; если a=–2, то решений нет; б) если a¹–2, то x=2; если a=–2, то решений нет; в) если a=–2, то x – любое число, кроме 3; если a¹–2, то x=2; г) если a=–8, то корней нет; если a=2, то корней нет; если