Обучение решению уравнений на уроках математики

в 5 классах на основе развития общеучебных действий

Уразаева Эльвира Салимжановна

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ .................................................................................................. 3

ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОБЛЕМЫ РАЗВИТИЯ

ОБЩЕУЧЕБНЫХ       ДЕЙСТВИЙ       УЧАЩИХСЯ       ПРИ       ОБУЧЕНИИ

МАТЕМАТИКЕ ................................................................................................... 6

1.1. Особенности развития общеучебных действий при обучении

математики в 5 классах ........................................................................................ 6

1.2 Содержание, средства, приемы и формы обучения математике для развития общеучебных  действий учащихся (на основании анализа школьных учебников математики 5 классов) ....................................................................... 18

ГЛАВА 2 ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ОБУЧЕНИЯ РЕШЕНИЮ УРАВНЕНИЙ В 5

КЛАССАХ,    ОРИЕНТИРОВАННЫЕ    НА    РАЗВИТИЕ    ОБЩЕУЧЕБНЫХ 

ДЕЙСТВИЙ ........................................................................................................ 26

2.1 Некоторые приемы обучения решению уравнений в 5 классах на основе развития общеучебных  действий ........................................................... 26

2.2 Урок общеметодологической направленности как одна из форм развития общеучебных действий учащихся 5 классов в процессе обучения

решению уравнений ............................................................................................. 38

ЗАКЛЮЧЕНИЕ ..................................................................................... .…60

БИБЛИОГРАФИЧЕСКИЙ СПИСОК........................................................ 61

ПРИЛОЖЕНИЕ .......................................................................................... 66

Приложение А .............................................................................................. 66 Технологическая карта 3 .............................................................................. 66

Приложение Б ............................................................................................... 81

Материалы по апробации результатов исследования: ............................... 81

-   Справка об апробации ............................................................................... 81

ВВЕДЕНИЕ

Современный этап общественного развития характеризуется рядом особенностей, предъявляющих новые требования к школьному образованию. Изменяются приоритеты и акценты в образовании, оно становится направленным на саморазвитие личности, на развитие у обучающихся таких качеств и умений, которые в дальнейшем должны позволить ему самостоятельно изучать что-либо, осваивать новые виды деятельности и, как следствие, быть успешным в жизни. Развитие личности в системе образования обеспечивается через развитие универсальных учебных действий, которые выступают инвариантной основой образовательного и воспитательного процесса.

В современной школе математика является одним из значимых предметов, с точки зрения её вклада в развитие интеллекта учащихся. Школьное математическое образование развивает воображение и интуицию, формирует навыки логического и алгоритмического мышления. Благодаря своей универсальности, математика вооружает учащихся методами познания других наук.

В сфере образования идет поиск нового содержания и новых форм обучения, создаются новые образовательные технологии, в связи с переменами, происходящими в обществе. Вместе с тем, в данной ситуации необходимо, чтобы учитель обладал высоким уровнем подготовки, владел большим запасом математических знаний, умел преподнести эти знания учащимся и организовать обучение школьников таким образом, чтобы они могли самостоятельно ставить вопросы, искать их решение, использовать различные источники информации.

Ведущее место в школьном курсе математики занимает линия уравнений. На их изучение отводится больше времени, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Линия уравнений является стержнем алгебраического материала школьного курса математики.

Фундаментом всего математического образования является курс математики 5 классов. Именно обучение в 5 классах обеспечивает познавательную мотивацию и интересы учащихся, их готовность и способность к сотрудничеству и совместной деятельности ученика с учителем и одноклассниками, сформировывает основы нравственного поведения, определяющего отношения личности с обществом и окружающими людьми. Поэтому, в 5 классах закладывается основа формирования учебной деятельности ученика – система учебных и познавательных мотивов, умение принимать, сохранять, реализовывать учебные цели, умение планировать, контролировать и оценивать учебные действия и их результат. 

Исследования показывают, что уровень математических знаний и умений в последние годы неуклонно падает. Поэтому важной проблемой методики преподавания математики является – поиск новых путей совершенствования процесса обучения. Один из таких путей – развитие универсальных учебных действий.

Проблема исследования: процесс обучения математике, ориентированный на развитие общеучебных действий у учащихся 5 класса.

Объектом исследования является процесс обучения математике в 5 классе.

Предметом исследования: обучение решению уравнений на уроках математики в 5 классах на основе развития общеучебных действий. 

Цель исследования: разработать дидактические материалы и методические рекомендации для обучения решению уравнений в 5 классе, ориентированных на развитие общеучебных действий.

Для достижения поставленной цели потребовалось решить следующие задачи:

-           проанализировать психолого-педагогическую   литературу по     теме исследования;

-           выявить возможности обучения решению уравнений на основе развития общеучебных действий;

-           провести обзор школьных учебников по математике для 5 классов: выявление заданий, ориентированных на развитие общеучебных

действий;

-           разработать методические рекомендации для развития общеучебных действий;

-           провести апробацию результатов исследования.

Методы исследования. Теоретические − изучение психологопедагогической, учебно-методической и математической литературы по теме исследования. Эмпирические – наблюдение за деятельностью учащихся в процессе обучения; организация и проведение опытного преподавания; анализ и обобщение результатов эксперимента.

Практическая значимость исследования: методические рекомендации для обучения решению уравнений с использованием вышеперечисленных методических приёмов и средств обучения, могут быть использованы учителями математики в 5-6 классах основной школы, с целью формирования необходимого уровня знаний учащихся и повышения уровня их общеучебных действий.

ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОБЛЕМЫ РАЗВИТИЯ ОБЩЕУЧЕБНЫХ ДЕЙСТВИЙ УЧАЩИХСЯ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ

1.1 Особенности развития общеучебных   действий при изучении

математики в 5 классах

Дети изучают прикладную математику в первые годы начальной школы. Их учат сравнивать количество, использование простых правил с жизненными явлениями, понятными им. Нет еще чисел, которые полностью отделены от реальной жизни. То есть, 1+2=3 - это не отвлечение для ребенка, не сложение 2 с числом 1. Это признак того, что все две вещи вы берете, если вы добавите еще одну вещь, вы получите три вещи. Дети еще не знают, что 2 можно понимать, как нечто, отвлекаемые от любых вещей, как чисто математическую концепцию, которая имеет свои особые свойства. Но они привыкли работать с ним так же по-разному, что они готовятся к новому способу взглянуть на цифры.

5 классах происходит переход к чистой математике: дети мастера общеобразовательной деятельности: работа с абстрактными числами, введены новые типы чисел (фракции и отрицательные числа), формируется понятие переменной и дается первые знания о методах. Принятие решений линейных уравнений, которые постоянно учатся решать текстовые проблемы, улучшить и обогатить навыки геометрических конструкций и измерений. Серьезное внимание уделяется развитию разумных навыков, простых доказательств, приведения обоснования для выполнения действий. В то же время закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных дисциплин. [17].

Курс математики 5 класса представляет собой органическую часть всей школьной математики. Поэтому основным требованием к его построению является структурирование содержания на единой идейной основе, которая, с одной стороны, является продолжением и развитием идей, реализованных при обучении математики в начальной школе, и с другой стороны, служит последующему изучению математики в старших классах.

Продолжается развитие всех содержательно-методических линий курса начальной математики: числовой, алгебраической, функциональной, геометрической, логической, анализ данных. Они реализованы на числовом, алгебраическом, геометрическом материале.

Представим некоторые особенности изучения предмета математики в 5 классе.

-         На первых порах изучения математики в 5 классе учащиеся повторяют известные им из 1-4 классов понятия, но повторение это ведётся на новом уровне, с привлечением математической терминологии и символики. Делается это для того, чтобы заложить основы математического языка, основы математической культуры.

-                В курсе 5 класса часто прибегают при изложении арифметики и начала алгебры к геометрическим определениям с помощью координатной прямой или луча, что позволяет сделать обучение более наглядным, а значит, более доступным и понятным для учащихся. Подобным образом, например, изучается сравнение обыкновенных и десятичных дробей.

-                Одной из особенностей данного курса является линейно-

концентрическое изложение материала, в соответствии с которым учащиеся неоднократно возвращаются ко всем принципиальным вопросам, поднимаясь в каждом следующем проходе на новый уровень [12].

В процессе развития общеучебных действий возникают некоторые существенные трудности.

Первая трудность, с которой встречаются пятиклассники, работа с объяснительным текстом учебника. Причина этого – недостаточная техника чтения у некоторых детей, малый словарный запас, а также и то, что в учебниках начальной школы такие объёмные тексты не встречались.

На протяжении всего времени обучения в 5-м классе учителям математики необходимо систематически развивать у детей умение читать, понимать текст, работать с ним. Эта работа служит необходимой базой для успешного изучения систематических курсов алгебры и геометрии в следующих классах.

Изучение математики требует активных умственных усилий. Очень трудно поддерживать произвольное внимание учащихся на протяжении всего урока. Напряжённая мыслительная деятельность, большое количество однотипных вычислений или алгебраических преобразований быстро утомляет школьников. Существует универсальный способ поддерживания рабочего тонуса учащихся: переключение с одного вида учебной деятельности на другой. Но можно воспользоваться и советом Блеза Паскаля: «Предмет математики настолько серьёзен, что полезно не упускать случаев, делать его немного занимательным». Данный совет особенно актуален при обучении математике в 5 классе [14].

Если в начальных классах обучение ведётся в основном на наглядно образном уровне мышления, то в 5-ом классе более глубоко развивается словесно-логическое мышление. Содержанием такого мышления являются понятия, сущность которых «уже не внешние, конкретные, наглядные признаки предметов и их отношения, а внутренние, наиболее существенные свойства предметов и явлений и соотношения между ними» [5, c. 23].

Все понятия, изучаемые в начальных классах, в дальнейшем переосмысливаются на более высоком теоретическом уровне (переменная, уравнение, фигура и др.) или углубляются и обобщаются (понятие о числе, алгоритмы арифметических действий, законы арифметических действий и д  р.).

Основные задачи, которые ставит перед собой учитель математики в процессе развития общеучебных действий учащихся в 5 классе:

-         обеспечить прочное и сознательное овладение системой математических знаний и умений, необходимых для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;

-         обеспечить интеллектуальное развитие, сформировать качества мышления, характерные для математической деятельности и необходимые для полноценной жизни в обществе;

-         сформировать умение учиться;

-         сформировать представление об идеях и методах математики,о математике как форме описания и методе познания окружающего мира;

-         сформировать представление о математике, понимание значимости математики для общественного прогресса;

-         сформировать устойчивый интерес к математике;

-         выявить и развить математические и творческие способности [30].

Чтобы выявить особенности развития общеучебных действий при обучении математики, рассмотрим более подробно само понятие «универсальные учебные действия» (рисунок 1).

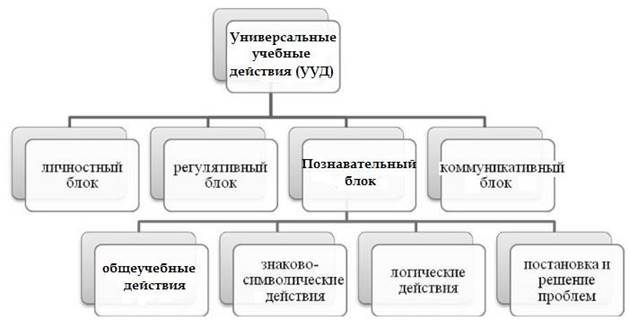
Рисунок 1. Универсальные учеб  ные действия

Развитие личности в системе образования обеспечивается через развитие универсальных учебных действий (УУД), которые выступают инвариантной основой образовательного и воспитательного процесса.

В широком значении термин «универсальные учебные действия» означает умение учиться, то есть способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта; совокупность действий учащегося, обеспечивающих его культурную идентичность, социальную компетентность, толерантность, способность к самостоятельному усвоению новых знаний и умений, включая организацию этого процесса [13].

В более узком (собственно психологическом) значении этот термин можно определить, как совокупность способов действия учащегося и связанных с ними навыков учебной работы, обеспечивающих его способность к самостоятельному усвоению новых знаний и умений, включая организацию этого процесса [13].

Универсальный характер учебных действий проявляется в том, что они:

-    носят надпредметный, метапредметный характер; 

-    обеспечивают преемственность всех ступеней образовательного процесса;

-    лежат в основе организации и регуляции любой деятельности учащегося независимо от её специально-предметного содержания.

Умение учиться предполагает полноценное освоение всех компонентов учебной деятельности, которые включают: познавательные и учебные мотивы, учебную цель, учебную задачу, учебные действия и операции. Выделяют четыре основных вида УУД: личностные, регулятивные, познавательные, коммуникативные (таблица 1) [29].

Таблица 1 – Виды универсальных учебных действий

Продолжение таблицы 1

Продолжение таблицы 1

Продолжение таблицы 1

Продолжение таблицы 1

Развивать УУД призваны все предметы учебного плана. Решение любой математической задачи, приводящейся к решению уравнения, развивает у учащихся все компоненты общеучебных действий (таблица 2). 

Таблица 2 – Развитие общеучебных действий в структуре учебной деятельности

Рассмотрим процесс развития общеучебных действий (рисунок 2), относящийся к группе познава тельных УУД (формулирование познавательной цели; поиск и выделение информации; знаково-символьное моделирование) при обучении решению уравнений.

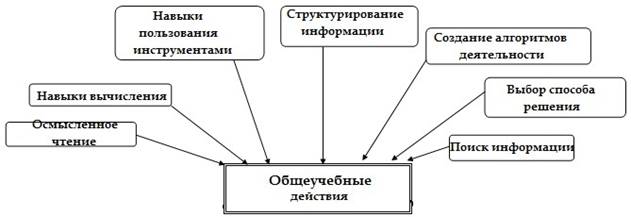
Рисунок 2. Общеучебные действия

Составим алгоритм учебных действий.

1.             Изучить содержание задачи, приводящей к уравнению (прочитать

текст);

2.             Провести анализ уравнения и поиск ее решения:

-         на основе анализа составить план решения (математическую схему) или сформулировать известный план решения такого класса уравнения;

-         решить уравнение по составленному плану;

-         проверить или исследовать решение;

-         рассмотреть другие возможные способы решения, выбрать наиболее рациональный способ;

-         записать ответ [13].

При изучении математики в школе в процессе вычислений, измерений, поиска решения задач, приводящихся к решению уравнений, у учеников развиваются умения: формулирования познавательной цели; осуществление поиска и выделение информации; знаково-символьное моделирование, создавая и преобразовывая их в соответствии с содержанием задания. Таким образом, происходит развитие общеучебных действий УУД.

В процессе изучения математики осуществляется знакомство с математическим языком формируются речевые умения: учащиеся учатся высказывать суждения с использованием математических терминов и понятий, формулировать вопросы и ответы в ходе выполнения задания, доказательства верности и неверности выполненного действия, обосновывают этапы решения учебной задачи. Работая в соответствии с инструкциями к заданиям, школьники учатся работать в парах и малых группах. Таким образом, происходит развитие умений формулирования познавательной цели.

Развитие общеучебных действий обеспечивается использованием поиска и выделения информации приемами самопроверки и взаимопроверки заданий. Учащимся предлагаются тексты для проверки, содержащие различные виды ошибок (графические, вычислительные, и т.д.). Для решения этой задачи можно совместно с учащимися составить правила проверки текста, определяющие алгоритм действий. В процессе работы школьник учится самостоятельно определять цель своей деятельности, планировать ее, самостоятельно двигаться по заданному плану, оценивать и корректировать полученный результат.

Развитие умений знаково-символьного моделирования обеспечивается умением самостоятельно определять и высказывать самые простые общие для всех людей абстрактные правила перевода реального мира в символьный [13].

1.2 Содержание, средства, приемы и формы обучения математике для развития общеучебных действий учащихся (на основании анализа школьных учебников математики 5 классов)

В ходе проведения исследования содержания материала, направленного на развитие общеучебных действий при обучении математике, были рассмотрены действующие учебники, входящие в федеральный комплект учебников. С точки зрения присутствия заданий, акцентированных на развитие общеучебных действий, наиболее подробно представлен анализ следующих учебников по математике для 5 класса (таблица 3):

С.М.Никольский, С.М.Потапов и д р.

Таким образом, учебники Г.В.Дорофеееав, И.Ф.Шарыгина и др., а также Г.К.Муравин, О.В.Муравина и др. позволяют вести разноуровневое обучение, обеспечивают качественную подготовку школьников к изучению систематического курса алгебры и геометрии (в том числе стереометрии) в старших классах, а также смежных дисциплин: физики, химии, географии и др. Учебники обеспечивают преемственность с курсом математики в начальной школе.

Таблица 3 – Анализ содержания учебников на наличие материала, направленного на развитие общеучебных действий

Продолжение таблицы 2

А вот структура учебников А.Г.Мерзляк, В.Б.Полонский и др., а также С.М.Никольский, С.М.Потапов и др. дает возможность максимально облегчить учителю подготовку к уроку: упражнения с помощью системы обозначений дифференцированы по трудности в четырех уровнях; в каждом параграфе сформулированы контрольные задания, исходя из того, что должны знать и уметь обучающиеся для достижения ими уровня стандарта математического образования; в конце учебника представлен раздел

«Домашние контрольные работы», который поможет педагогу сориентировать учеников на необходимый им уровень трудности. Теоретический материал учебников ориентирован на проблемный подход в обучении, на организацию поисково-эвристической и коммуникативной деятельности школьников. Цветные иллюстрации (рисунки и схемы) обеспечивают высокий уровень наглядности учебного материала.

Анализ учебников под редакцией Г.В.Дорофеева, И.Ф.Шарыгина и под редакцией А.Г.Мерзляк, В.Б.Полонский, используемых в большинстве образовательных школ показал, что, работая по данным учебникам, учащиеся имеют возможность овладевать отдельными видами общеучебных действий, однако, возможности учебников ограничены. Их содержание в большей степени способствует формированию логического мышления. Однако в учебниках отсутствует соответствующая система заданий, необходимых для развития умений постановки вопросов, а именно, нет заданий, где требуется написать план решения задачи, самостоятельно составить условие задачи по имеющемуся рисунку и провести оценку представленного решения. Также в данных учебниках мало заданий, где нужно обосновать свой ответ, способ решения, само решение или мнение относительно определенного случая. Методические подходы не всегда способствуют самостоятельному открытию учащимися новых знаний. В основном они рассчитаны на отработку изученного материала.

В связи с этим, необходимо разработать методические рекомендации, ориентированные на развитие различных компонентов общеучебных действий, которые позволили бы учителю готовиться к урокам и проводить их.

Рассмотрим формы, методы и приемы обучения математике, наиболее характерные для развития общеучебных действий.

Одним из эффективных средств, способствующих развитию общеучебных действий, является создание проблемных ситуаций на уроке. На таком уроке реализуется исследовательский подход к обучению, принцип деятельности, смысл которого заключается в том, что ребенок получает знание не в готовом виде, а «добывает» его в процессе своего труда. В процессе такой систематической работы на уроке развиваются не только познавательные, но и дополнительно регулятивные и коммуникативные действия. Учащиеся учатся фиксировать затруднения в собственной деятельности, выявлять причины этих затруднений, определять цель своей дальнейшей работы, выбирать средства и способы достижения поставленной цели, осуществлять поиск необходимой информации. Ученики учатся сравнивать, анализировать, делать вывод, формулировать свое мнение и позицию, координировать различные позиции в сотрудничестве.

Важнейшую роль в развитии общеучебных действий играет работа с текстом. Навык чтения по праву считается фундаментом всего образования. Полноценное чтение – сложный и многогранный процесс, предполагающий решение таких познавательных задач, как понимание (общее, полное и критическое), поиск конкретной информации, самоконтроль, восстановление широкого контекста, интерпретация, комментирование текста и многое другое. В деятельности чтения участвуют такие механизмы, как восприятие, узнавание, сличение, понимание.

Дискуссия – еще одно средство развития общеучебных действий школьников. Диалог учащихся может проходить не только в устной, но и письменной форме. Следует обратить внимание на развитие тех умений постановки целей, которые являются предпосылкой успешно проведенной письменной дискуссии: четко письменно излагать свое мнение, понимать точки зрения своих одноклассников, выраженные письменно, задавать вопросы на понимание.

Проектная и исследовательская деятельности – необходимое условие компетентного подхода и действенное средство развития общеучебных действий. В процессе этих видов деятельности у учащихся развивается весь спектр познавательных УУД. Исследования учащихся обеспечивают высокую информативную емкость и системность в усвоении учебного материала, широко охватывают внутри предметные и междисциплинарные связи.

Рефлексия – одно из важнейших средств развития общеучебных действий, таких как умения учиться. К средствам, развивающим общеучебные действия на стадии рефлексии, помогающие творчески интерпретировать информацию, относятся: составление задач, памятки, инструкции, схемы и др.

Интеграция выше названных средств позволит осуществлять целенаправленное развитие общеучебных действий у учащихся и в конечном счете повысить качество знаний по предмету и создать условия для успешной социализации личности.

Также, успешное развитие общеучебных действий гарантирует выбор метода обучения. В настоящее время насчитывается более 50 методов: рассказ, упражнения, работа с источниками, беседа, самостоятельная работа, игра и т.д.

Метод проблемного изложения состоит в том, что учитель, прежде чем излагать материал, ставит проблему, формулирует задание, а лишь затем, раскрывая систему доказательств, сравнивая и сопоставляя различные точки зрения, показывает способ его решения. Все эти действия сопровождаются использованием различных источников и средств. Происходит научный поиск, где учащиеся становятся его свидетелями и соучастниками. На основе анализа фактов и раскрытой системы доказательств учащиеся самостоятельно делают выводы и обобщения, формируют с помощью учителя определенные понятия и правила.

Частично-поисковый (эвристический) метод состоит в организации активного поиска решения выдвинутых учителем или самостоятельно сформулированных учащимися заданий. Организация поиска решения происходит под руководством учителя или на основе эвристических программ. При этом методе способ поиска решения проблемы определяет учит ель, но сами решения отдельных вопросов находят учащиеся. Они самостоятельно подходят к формулированию правил, свойств, теорем и составлению заданий. При этом процесс мышления учащихся поэтапно направляется и контролируется учителем или самими учащимися на основе работы с учебными пособиями (в нашем случае при помощи разработанных письменных диалоговых заданий). Данный метод возбуждает интерес к познанию, побуждает к самостоятельности и активизирует мышление.

Исследовательский метод состоит в самостоятельном поиске учащимися варианта решения. После проведенного анализа материала, постановки проблем и задач, устного или письменного пояснения учителя учащиеся самостоятельно изучают представленный материал, ведут наблюдения и измерения и выполняют различные действия поискового характера. В исследовательской деятельности у учащихся наиболее полно проявляются инициатива, самостоятельность, творческий поиск.

Выводы по первой главе

Вместе с приемами, методами и средствами обучения, на продуктивность развития общеучебных действий учащихся и обучения в целом влияет форма организации обучения, наиболее доступная для изменения и совершенствования со стороны учителя. На основе проведенного анализа пришли к выводу, что для нашего исследования в большей степени подходит организация урока общеметодологической направленности с реализацией групповой формы обучения и работы в парах. Групповая форма работы и работа в парах во время урока общеметодологической направленности развивает не только общеучебные действия, но и предоставляет учащимся возможность:

-       осуществлять взаимопомощь;

-       распред  елять обязанности между учащимися в группе;

-       соревноваться друг с другом;

-       развивать чувство ответственности за собственный результат;

-       проводить сравнение и анализ проделанной работы в своей и в других группах;

-       оценивать результат совместной деятельности;

-       работать в группе в различных ролях (лидер, исполнитель, критик), тем самым всячески учувствовать в выработке решения задания;

-       вырабатывать правила поведения, которые присущи всем людям и способствуют тому, чтобы решать проблемы и различные задачи;

-       учащиеся учатся оценивать действия и поступки друг друга;

-       у них снижается страх за ошибки перед учителем и другими учениками;

-       у учащихся имеется возможность работать в различных ролях (ведущий в роли учителя, исполнитель в роли ученика), что способствует выработке решения задания при обучении и развитию умений выявлять проблему, осуществлять поиск и оценку способов её решения;

-       попеременно выступая в роли ученика или учителя, у учащихся повышается ответственность за свои знания;

-       активизируется познавательная деятельность;

-       развивается инициативность, коммуникабельность и трудолюбие.

Таким образом, систематическое использование различных методических приёмов свидетельствуют о возможности развития общеучебных действий у учащихся при обучении математике в 5 классе, которые позволяют повысить эффективность обучения математике.

ГЛАВА 2 ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ОБУЧЕНИЯ РЕШЕНИЮ УРАВНЕНИЙ В 5 КЛАССАХ, ОРИЕНТИРОВАННЫЕ НА РАЗВИТИЕ ОБЩЕУЧЕБНЫХ ДЕЙСТВИЙ

2.1 Некоторые приемы обучения решению уравнений в 5 классах на основе развития общеучебных действий

С учетом рассмотренных ранее средств, методов и форм обучения, ориентированных на развитие УУД, выделим рекомендации по развитию общеучебных действий познавательных УУД.

Для того чтобы ученики усвоили материал по предмету, их необходимо научить мыслить системно (например, основное понятие (правило) – пример – значение материала). Важно помочь ученикам овладеть наиболее продуктивными методами учебно-познавательной деятельности, научить их учиться. Учителю всегда необходимо помнить, что знает не тот, кто пересказывает, а тот, кто использует на практике, поэтому на этом этапе нужно найти способ научить школьника применять свои знания. Только творческое мышление можно развивать всесторонним анализом проблем, для этого уравнения необходимо научить решать несколькими способами.

Выделим основные особенности обучения решению уравнений в 5-6

классах.

Уравнения в школьном курсе математики занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений [25].

Линия уравнений и неравенств является стержнем алгебраического материала школьного курса математики.

Обучение учащихся умению решать уравнения начинается уже в начальной школе. У учеников формируется понятие уравнения, как равенства с неизвестным числом, которое требуется найти. Используя правила нахождения неизвестных компонентов, дети учатся находить корни простейших уравнений. Свое дальнейшее развитие содержательнометодическая линия уравнений получает в 5-6 классах, причем на этом этапе уже есть возможность и необходимость показать детям прикладную ценность уравнений.

Понятие уравнения является ведущим алгебраическим понятием. Эта линия развертывается в трех основных направлениях [13]:

-       прикладная направленность;

-       теоретико-математическая направленность;

-       направленность на установление связей с остальным содержанием.

Уравнения и неравенства являются стержнем алгебраического материала. В их изучении выделяются три больших этапа:

-       пропедевтика уравнений и неравенств в начальной школе;

-       более высокий уровень пропедевтики в 5-6 классах;

-       решение различных видов уравнений и неравенств с 7 класса.

В 5 классе (второй этап) учащимся предлагается к изучению следующие определения:

-         «Равенство, содержащее неизвестное число, называется уравнением»;

-         «Найденное значение неизвестного числа называется корнем уравнения»; «Решить уравнение – значит найти его корни».

В 5 классе в процессе развития общеучебных действий можно организовать решение уравнений на основе использования взаимосвязи

между компонентами и результатами арифметических действий и обобщаются правила:

-       нахождение слагаемого;

-       нахождение, уменьшаемого;

-       нахождение вычитаемого;

-       нахождение множетеля;

-       нахождение делимого;

-       нахождение делителя.

Первые уравнения содержат переменную только в одной части. Позднее уравнения усложняются, и появляется возможность перейти к более высокому уровню развития общеучебных действий познавательных УУД.

При решении ученики рассуждают по следующему плану:

-       неизвестное число входит в состав делителя. Найдем делитель, разделив делимое на частное;

-       неизвестное число является уменьшаемым. Найдем его, сложив вычитаемое с разностью.

Затем рассматривается решение задач с помощью составления уравнений.

В 5-м классе изучаются уравнения, которые содержат буквенные выражения только в одной части уравнения. При их решении развиваются общеучебные действия такие, как внимание, которое у учащихся сосредотачивается на выделение способа решения, осмысление понятия корня и на понимании постановки задачи о решении уравнения. Для облегчения усвоения различных методов и способов решения уравнения в систему подготовленных упражнений включаются задания на упрощение числовых и буквенных выражений, нацеленные на прочное усвоение учащимися правил умножения или деления разнообразных произведений на некоторое отличное от нуля число.

Таким образом, при решении уравнений и неравенств в 5 классах учащиеся формируют базовые знания по определению понятия уравнения как равенства, содержащего неизвестное число, переменную величину. Обучаются решению линейных уравнений, составления уравнения для решения текстовых задач. Изучение и решение уравнений на уроках математики в 5 классах дает возможность для развития общеучебных действий познавательных УУД (таблица 4).

Таблица 4 - Развитие общеучебных действий средствами предмета «Математика» 

Продолжение таблицы 4

Рассмотрим некоторые из приведенных в таблице 3 заданий подробнее. 

Роль проблемной задачи в развитии общеучебных действий состоит в том, что проблемные ситуации практически всего курса математики строятся на затруднении в выполнении нового задания. То есть учащиеся сначала получают задание решить задачу, которую они могут решить. Затем дается задача, похожая на предыдущую, но при этом измененная так, что у детей возникают затруднения. Возникает вопрос «а почему мы не можем ее решить?». После этого возникает вопрос «а как ее решить?». Например, на уроке по теме «Использование букв для обозначения чисел, вычисление значения алгебраического выражения» в 5 классе можно предложить следующий этап постановки учебной задачи.

Задание 1. 

Какое из чисел 3,12,14 является корнем уравнения:

1)  х+16=28; 2)  4х-5=7.

Учащиеся решают эти уравнения. 

х+16=2, х=28-16, х=12.

Ответ (1): 12.

4х-5=7, 4х=7+5, 4х=12, х=12/4, х=3.

Ответ (2): 3.

Задание 2. 

Решить уравнения

(134+х)-583=426 и 3128-(m+425) = 1509.

Школьники испытывают затруднение, так как они умеют решать

уравнения только с помощью связи между компонентами действий, а в этих уравнениях больше одного неизвестного компонента действия. С помощью наводящих вопросов учителя учащиеся формулируют цели и тему урока. В конце урока необходимо вернуться к этим уравнениям и решить их, применив знания, приобретенные на уроке.

Роль такого приема обучения как работа с учебником в развитии общеучебных действий состоит в том, что школьники могут самостоятельно выполнять по тексту учебника то или иное задание. Приведем примеры.

1)                  Найти задание по оглавлению.

2)                  Обдумать заголовок (ответить на вопросы: «О чем пойдет речь?», «Что мне предстоит узнать?», «Что я уже знаю об этом?»).

3)                  Прочитать содержание пункта параграфа; выделить все непонятные слова и выражения, выяснить их значение (в Интернете, справочнике, словаре).

4)                  Задать походу чтения вопросы и ответить на них (О чем здесь говорится? Что мне уже известно об этом? Что именно об этом сообщается? Чем это можно объяснить? Как это соотносится с тем, что я уже знаю? С чем это нужно не перепутать? Что из этого должно получиться? К чему это можно применить?).

5)                  Выделить основные понятия в тексте.

6)                  Выделить основные теоремы ил  и правила.

7)                  Изучить определения понятий, теорем (правил).

8)                  Изучить теоремы (правила).

9)                  Разобрать конкретные примеры в тексте и придумать свои.

10)              Самостоятельно провести доказательство теоремы.

11)              Составить схемы, рисунки, чертежи по имеющейся информации. 

12)              Запомнить материал, используя приемы запоминания (пересказ по схеме, мнемонические приемы, повторение трудных мест).

13)              Ответить на конкретные вопросы в тексте.

14)              Придумать и задать себе вопросы.

Очень полезно, развивая общеучебные действия на уроках математики, устраивать дискуссии. Можно, например, разделить класс на четыре группы. Первой и второй группе дается первая задача и решение второй задачи, третьей и четвертой группе дается решение первой задачи и вторая задача. Каждая группа независимо от других решает свою задачу. Затем первой и второй группам задается вопрос, и тот, кто из них ответит быстрее, будет выбирать, кому показывать решение первой задачи, а кому быть оппонентом. Итак, один учащийся у доски показывает полное решение задачи со всеми обоснованиями, а другой учащийся – его оппонент – внимательно слушает, а затем или оспаривает решение, или соглашается с ним, также обосновывая свои действия. Третья и четвертая группы при этом являются экспертами, которые затем высказывают свое мнение о ходе дискуссии, опираясь на готовое решение задачи. После этого группы меняются ролями и приступают к обсуждению решения второй задачи. Одновременно можно рассмотреть и другие способы решения данных задач. 

Задание 3 (На выполнение прикидки).

Решите уравнение и округлите результат до сотен:

1) 234 + у = 452;  2) 378 - х = 165.

Задание 4 (На знание математического языка).

Цена хризантемы – а р. з  а один цветок, а цена одной розы – на 30 р.

больше. Запишите на математическом языке: цену розы; стоимость пяти хризантем; стоимость трех роз; стоимость букета изпяти хризантем и трех роз. 

Развитие общеучебных действий происходит наиболее эффективно, если использовать математическую модель.

Задание 5.

Расшифруйте данные математические модели в соответствии с каждой из конкретных ситуаций (таблица 5).

Таблица 5 - Математические модели

Развитие общеучебных действий, учащихся проходит успешно, если учитель дает задания на самопроверку и взаимопроверку. Рассмотрим организацию работы на примере проведения математического диктанта. 

Задание 6 (Математические диктанты). 

1.            На доске заранее написаны ответы. После написания диктанта ответы открываются, и каждый ученик самостоятельно проверяет свою работу и оценивает ее, согласно критериям, предложенным учителем. Данный вид проверки, прежде всего, направлен на развитие внимания и умения адекватно оценивать себя самого. 

2.            Ученики меняются тетрадями и осуществляют взаимопроверку, с последующей проверкой учителем или с последующим обсуждением в паре допущенных ошибок. Появляется элемент ответственности за партнера, развивается внимание, появляется необходимость начать обсуждение ошибок, а значит вступить в диалог. 

3.            Каждый обучающийся самостоятельно оценивает свою работу, еще не зная ответов, то есть, опираясь на интуицию или реально представляя свои знания. После этого осуществляется взаимопроверка. Результаты сравниваются, и выставляется итоговая оценка. 

Развитие общеучебных действий, учащихся возможно и средствами головоломок и загадок. Нужно по ответу отгадать вопрос.

 Задание 7. 

Например, число, которое делится только на себя и на единицу. Какой был задан вопрос? «Угадай, о чем меня спросили?». 

Задание 8. 

Найдите значение числа, а, если 8,

а + 9 х = 60 и х= 4.

Задание 9. 

Петя задумал число. Если к этому числу прибавить 43, а к полученной сумме прибавить 77, то получится 258. Какое число задумал Петя?

Задание 10. 

Упростите выражения, назовите свойства:

а) 42 – (15 + а);

б) (874 + х) – 74;

в) 52 + с + 12;

г) n – 25 – 35.

Задание 11.

Составить кроссворд из 10 слов по теме «Уравнения».

 Задание 12.

Математический фокус. Загадайте число. Прибавьте к нему 12, затем отнимите 7 и прибавьте. Какое число у вас получилось?

Задание 13.

Решите задачу с помощью уравнения. В корзине было несколько грибов. Через некоторое время в корзину положили 11 грибов, а потом ещё 20, после чего в корзине стало 43 гриба. Сколько грибов было первоначально в корзине?

Задание 14. 

Найдите ошибку:

(х – 12) + 10 = 32;

х – 12 = 32 – 10;

х – 12 = 22;

х = 22 – 12;

х = 10.

При развитии общеучебных действий, учащихся можно использовать такой прием как работа с карточками (таблицы 6 и 7).

Таблица 6 - Задание 15

Нестандартные задания активизируют рябят и, тем самым, способствуют развитию общеучебных действий учащихся.   

Задание 16. 

Вместо звёздочки подставить такое число, чтобы получилось уравнение, корнем которого было бы число данное

а) *+5=2x+1; (*=4)

б) 3x-7=*-2; (*=7)

в) (5x+1)2=*-3.        (*=45)

Задание 17. 

Разделите уравнения на группы, в которых неизвестный компонент находится одинаковым действием

1)                 х + 12 = 45;

2)                 b – 19 = 60;

3)                 256 – (y + 112) = 25;

4)                 60 = b + 19;

5)                 k – 0 = 92;

6)                 6)       162 = c – 47;

Задание 18. 

Составьте по условию задачи уравнение и решите его: «В корзине было 15 груш. Сначала из нее взяли 7 груш, а потом положили в нее неизвестное количество груш. В результате в корзине стало 34 груши. Сколько груш положили в корзину?».

Таким образом, развитие общеучебных действий, учащихся успешно реализуется в процессе обучения решению уравнений и задач, приводящихся к уравнениям.

2.2Урок общеметодологической направленности, как одна из форм развития общеучебных действий учащихся 5 классов в процессе обучения решению уравнений

Развитию общеучебных действий, учащихся способствует проведение уроков разных типов и видов. На уроке общеметодологической направленности, учащиеся сами формулируют цели и задачи урока, учитель всего лишь подводит к осознанию целей и задач. Учащиеся сами планируют способы достижения целей урока, а учитель консультирует. Во время практической деятельности учащиеся осуществляют учебные действия по намеченному плану, учитель помогает и советует. Во время урока учащимися осуществляется контроль: применяются формы самоконтроля, взаимоконтроля. Возникшие затруднения во время урока, учащиеся формулируют и осуществляют коррекцию самостоятельно, советуясь с учителем. В конце урока дается оценка деятельности учащихся по ее результатам, проводится рефлексия. Домашнее задание формулируется так, что ученики могут выбирать задание из предложенных учителем, с учетом индивидуальных возможностей.

В данном пункте представлены разработанные автором уроки общеметодологической направленности, с учетом:

-             особенностей, учащихся в 5 классах; 

-             рассмотренных приемов, средств, методов и форм обучения;

-             возрастных особенностей обучения учащихся 5 классов. 

При разработке урока общеметодологической направленности применялись представленные ниже приемы, развивающие общеучебные действия пятиклассников.

Элементы истории математики. Использование элементов истории математики позволяет включить учащихся в поиск новых смыслов и альтернативных интерпретаций изучаемого математического материала, увидеть значения изучаемых понятий, увидеть данное понятие в связи с другими, научить школьников быть толерантными к иному мнению, адекватно принимать различные способы рассуждений, что создает условия для обогащения различных форм умственного опыта учащихся. На первый взгляд кажется трудным найти на уроке время, необходимое для ознакомления с историческим материалом. Однако вопрос о формах использования элементов истории математики на уроках почти полностью подчинен главному вопросу – связи изучаемой в школе математики с историей. Какая бы ни была форма сообщения исторических фактов: краткая беседа, экскурс, лаконичная справка, решение уравнения, показ и разъяснение рисунка, – использованное время нельзя считать потерянным напрасно, если учитель сумел преподнести исторический факт в тесной связи с изучаемым на комбинированном уроке теоретическим материалом.

Работа с информацией. Обучение в процессе развития общеучебных действий больше не заключается в том, что ученик получает от учителя некую информацию и осваивает ее. Чем лучше учитель учит детей решать конкретные уравнения, чем больше дает им технических умений, тем труднее им решать задачи нестандартные и новые. Ученики пасуют перед новым. Эту проблему можно решить, если систематически развивать общеучебные действия.

Особое место на уроках общеметодологической направленности по обучению решения уравнений занимает текстовая информация в научном стиле. Целями научного сообщения являются: по возможности точное и полное объяснение фактов, демонстрация причинно-следственных связей между явлениями, выявление закономерности исторического развития и т. д. 

Практико-ориентированные задачи, приводящиеся к необходимости решать уравнения. Огромное значение в развитии общеучебных действий имеют задачи с практическим содержанием, которые целесообразно использовать в процессе обучения решению уравнений, через раскрытие многообразия применения математических задач в жизни, своеобразия отражения ею реального мира и достижения дидактических целей, таких как:

-            мотивация введения новых математических понятий и методов;

-            иллюстрация учебного материала;

-            закрепление и углубление знаний по предмету;

-            развитие практических умений и навыков.

Устные упражнения. Среди различных форм работы на уроке общеметодологической направленности по обучению решения уравнений следует особенно выделить чрезвычайную полезность решения уравнений устно. Устные упражнения содержат огромные потенциальные возможности для активизации познавательной деятельности учащихся. Во время выполнения устного решения уравнений активизируется мыслительная деятельность учащихся, развивается память, речь, внимание, способность воспринимать сказанное на слух, быстрота реакции, наряду с этим развивается и гибкость мышления. Эти функции устных упражнений тесно связывают их с теорией развивающего обучения, которая определяет основную цель обучения в развитие интеллектуальных способностей учащихся. В частности, в качестве одного из средств развивающего обучения предлагается система устных упражнений.

Все вышесказанное реализовано в представленных технологических картах к урокам общеметодологической направленности по следующей тематике:

1)«Решение уравнений» (таблица 8);

2)«Решение задач с помощью уравнений» (таблица 9);

3)«Решение нестандартных задач, приводящихся к уравнению» (приложение А, таблица А.1), которые проводились в 5-х классах, обучающихся по учебнику Н. Я. Вилкина, В.И. Жохова и др., после изучения темы «Решение уравнений». 

Технологическая карта 1

Тема урока: «Решение уравнений»

 Цели (задачи) урока

-    Образовательные: актуализировать знания учащихся об уравнениях, полученные в начальной школе, дать понятие корня уравнения, познакомить учащихся с алгебраическим способом решения задач.

-    Воспитательные: способствовать воспитанию аккуратности, усидчивости, прилежности, формирование личностных позитивных качеств школьников, создание атмосферы сотрудничества учителя и учащихся, воспитание трудолюбия, чувства коллективизма, привитие интереса к изучаемому предмету, воспитание сознательного усвоения дисциплины.

-     Развивающие: способствовать развитию умения сравнивать, обобщать, анализировать; развивать умение составлять план и пользоваться им.

Основные понятия: уравнение, корень уравнения, решить уравнение.

Планируемые образовательные результаты:

-    предметные: уметь решать уравнения;

-    личностные: уметь осуществлять самооценку на основе критерия успешности учебной деятельности; осознать ответственность за общее дело; понимать причины успеха (неуспеха) в учебной деятельности;

-    метапредметные: 

a)     регулятивные – уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; планировать свое действие в соответствии с поставленной задачей; высказывать свое предположение; 

b)    коммуникативные – уметь оформлять свои мысли в устной форме; слушать и понимать речь других; уметь выражать свои мысли с достаточной полнотой и точностью; 

c)     общеучебные действия:

-    формулирование познавательной цели: уметь ориентироваться в своей системе знаний; добывать новые знания; 

-    поиск и выделение информации: уметь осознанно и произвольно строить речевые высказывание; самостоятельно создавать алгоритмы деятельности; 

-    знаково-символьное моделирование: извлекать из математических текстов необходимую информацию; строить логическую цепочку рассуждений.

Оборудование урока: учебник, письменные принадлежности, тетрадь

    Домашнее задание: п.10,          с.58          –       60, №395,    №397

Таблица 8 – Технологическая карта к уроку 1

Продолжение таблицы 8

Технологическая карта 2

Тема урока: «Решение задач с помощью уравнений» 

Образовательные ресурсы: Математика 5 класс. Учебник для учащихся Н. Я. Виленкин, Интернет – ресурсы.

Методы обучения: частично-поисковый, наглядный, словесный.

Используемые технологии: технология проблемного обучения.

Познавательные УУД:

а) общеучебные действия:

-            формулирование познавательной цели: уметь ориентироваться в своей системе знаний; добывать новые знания;

-            поиск и выделение информации: уметь искать информацию в учебной книге, ориентироваться в своей системе знаний; 

-            знаково-символьное моделирование: извлекать из математических текстов не информацию; строить логическую цепочку рассуждений.

б) логические действия: построение логической цепи рассуждений. 

Регулятивные УУД: оценивать правильность выполнения действий на уровне адекватной оценки. 

Личностные УУД: способность к самооценке. 

Коммуникативные УУД: уметь сотрудничать в совместном решении проблемы.

Планируемые результаты:

-            предметные: уметь решать уравнения, решать задачи с помощью уравнения;

-            метапред метные: уметь высказывать своё предположение;

-            личностные: формирование устойчивой мотивации.

Таблица 9 – Технологическая карта к уроку 2

Продолжение таблицы 9

Продол жение таблицы 9

Продолжение таблицы 9

Продолжение таблицы 9

После проведения уроков общеметодологической направленности, на основании наблюдения и беседы с учащимися и коллегами, были выявлены следующие положительные особенности:

-            проведённые уроки были интересны ученикам и неутомительны;

-            на уроках были включены в учебную деятельность все ученики;

-            ученики выполняли как самостоятельные, так и групповые задания;

-            дети активно контактировали друг с другом, обсуждали задания и возникающие вопросы, оценивали работу друг друга;

-            ученики самостоятельно искали и определяли способы решения задач, находили ответы.

Выводы по второй главе

На основании проведенного исследования выделим основные пути совершенствования урока математики общеметодологической направленности, направленного на развитие общеучебных действий пятиклассников:

-            усиление целенаправленности деятельности учителя и учащихся на уроке: мотивация учащихся на выполнение поставленных задач, достижение целей непосредственно на уроке;

-            осуществление четкой организации каждого урока от первой до последней минуты: планирование урока общеметодологической направленности таким образом, чтобы в нем были предусмотрены самые короткие пути, ведущие к поставленной цели;

-            повышение познавательной самостоятельности и творческой активности учащихся: применение на уроке общеметодологической направленности методов и приемов проблемного обучения; организация самостоятельной работы учащихся с различными источниками информации;

-            интенсификация учебно-воспитательного процесса на уроке общеметодологической направленности: степень интенсивности учебного труда зависит от эффективности использования каждой минуты урока, мастерства учителя, подготовки учащихся, организованности классного коллектива, наличия необходимого оборудования и т.п., в то же время не следует понимать под интенсификацией стремление решить, как можно больше уравнений.

-            совершенствование структуры урока общеметодологической направленности: использование в работе современных образовательных технологий позволяет учителю конструировать самые разнообразные по типу и структурным элементам уроки.

Безусловно, можно привести еще целый ряд конкретных примеров, подтверждающих богатый потенциал урока математики общеметодологической направленности для развития общеучебных действий. Да и в самом содержании математики заложен инструмент этого обучения и развития.

ЗАКЛЮЧЕНИЕ

Овладение учащимися общеучебными действиями выступает как способность к саморазвитию и самосовершенствованию, путем сознательного и активного присвоения нового социального опыта, то есть умения учиться. В данной работе, с учетом особенностей обучения математике в 5 классах средней школы, были выявлены основные приемы, средства, методы и формы обучения, основанные на формировании УУД. С учетом этого, разработаны методические рекомендации по обучению решению уравнений в 5 классах.

Практическая значимость результатов исследования состоит в возможности использования материалов исследования учителями при разработке отдельных уроков математики, а также для создания системы работы и методики преподавания. Кроме того, внедрение в педагогическую практику описанных методических рекомендаций позволит осуществить метапредметный подход к образованию школьников и развить общеучебные действия.

В процессе работы проанализирована литература по проблеме развития общеучебных действий на уроках математики в 5 классах, определены особенности обучения решению уравнений, разработаны методические рекомендации, получены успешные отзывы при апробации материалов исследования. 

БИБЛИОГРА ФИЧЕСКИЙ СПИСОК

1.            Актуа льные вопросы форм ирования инте реса в обуч ении: учеб. посо бие / под ре д. Г. И. Щукина. – М.: Просвещение, 1984. – 176 с.

2.            Аммосова, Н.В. Тождест  венные преобразования, уравн ения и нераве нства в 5 кла ссе / Н.В.Аммосова // Матем атика в шко ле, 1996.  – №3. – с.54-58.

3.            Ау т, К.Х. О ро ли основных принц ипов дидактики в преподавании ш кольного кур са математики / К. Х. Ау т, Н. Я. Виленкин // Матем  атика в шко ле. – 1987. – №1. – С. 41-44.

4.            Бабан ский, Ю. К. Оптимизация уче бно-воспитательного проц есса /Ю. К. Бабанский. – М.: Просвещение,1982. – 192 с.

5.            Березанская, Е. С. Мето дика арифметики: посо бие для учит  елей сред. шко лы / Е. С. Березанская. – М.: Учпедгиз, – 1955. – 542 с. 

6.            Боженкова, Л. И. Мето дика формирования универс  альных учебных дейс твий пр и обучении геоме трии / Л. И. Боженкова. – М.: БИНОМ. Ла б. знаний, 2013. – 205 с.

7.            Возрастные и индивидуальные особен ности младших по дростков / по д ред. Д.Б.Элько нина, Т.В. Драгуновой. – М. Просвещение, 1976. – 360 с.

8.            Волович, М.Б. Ка к обеспечить усво ение математики в 5 классе: Методи ческое пособие / По д ред. А.Г. Мордк  овича. – М.: Вет  ана-Графф – Моза ика-Синтез. 2003.  – 64 с. 

9.            Гнеденко, Б.В. Матем атика и математ  ическое образован ие в соврем енном мире / Б.В. Гнед  енко. – М. Просве щение, 1985. – 192 с. 

10.       Зуба рева, И. И. Математика. 5-6 кла ссы: метод. посо бие для учит  еля / И. И. Зубарева, А. Г. Мордк  ович. – 4-е из  д., испр. – М.: Мнемозина, 2014. – 120 с. 

11.       Зубарева, И.И. Матем атика. 5 класс : уч еб. Для учащ ихся общеобразоват. учреж дений / И.И.Зубарева, А.Г.Мордк  ович.  – М.:

Мнемо зина, 2013. – 270 с.

12.       Зуба рева, И.И. Математика. 6 кла  сс [Текст]: уч еб. Для учащ  ихся общеобразоват. учреж дений / И.И.Зубарева, А.Г.Мордк  ович. –М.: Мнемо зина, 2013. – 264 с.

13.       Ка к проектировать универс  альные учебные дейс  твии в начал ьной школе: о т действия к мысли: учеб  ное пособие дл  я учителя / [А.Г. Асмо лов, Г.В. Гурменская, И.А. Волода  рская и д р.]; под ре д. А.Г. Асмолова. – М.:

Просвещение, 2008. – 151 с.

14.       Квитко, Е. С. Возмож ности математики в формировании универс альных учебных дейс твий в 5-6 кл ассах с использованием ИК Т / Е. С. Квитко // Вест  ник МГПУ. Сер  ия «Информатика и информатизация образо вания». – 2013. – № 2(26). – 128 с. – с. 108-115.

15.       Квитко, Е. С. Методи ческие приёмы обуч ения математике в 5-6 классах, направ ленные на разв  итие универсаль ных учебных дейс  твий / Е. С. Квитко // Пер  спективы нау ки. – 2014. – № 3. – с. 19-23.

16.       Кин пис, И.М. Задачи н а составление уравн ений и нерав енств [Текст] / И.М. Кин  пис. – М.: Просве щение, 1995. -84 с.

17.       Леви тас, Г.Г. Методика препод  авания математике в основной шко ле [Текст]: учеб  ное пособие / Г.Г. Леви  тас. – Астрахань: Издате льский дом «Астрах анский университет», 2009. – 179 с.

18.       Лященко Е.И., Маза ник А.А. Методика обуч ения математике в 56 классах. – Мин ск: Народная асв ета, 1976. -92 с.

19.       Матем атика,       5-6:   кн.     дл я   учителя      /        [С.     Б.       Суво рова,

Л. В. Кузнецова, С. С. Мина ева, Л. О. Рослова]. – М.: Просвещение, 2006. – 191 с.

20.       Математика. 5 кла сс: учеб. дл  я учащихся общеобр  азоват.

учреждений / Н. Я. Виле нкин, В. И. Жохов, А. С. Чесн оков [и д р.]. – 31-е из  д., стер. – М.: Мнемозина, 2013. – 280 с. 

21.       Математика. 6 кла сс [Текст]: уч еб. для учащ  ихся общеобразоват.

учреж дений / Н. Я. Виленкин, В. И. Жох  ов, А. С. Чесноков [и др.]. – 30-е изд., ст  ер. – М.: Мнемо зина, 2013. – 288 с.

22.       Приме рная         основная    образова  тельная          программа

образова тельного учреждения. Осно вная школа / Со ст. – Е.С. Савинов. – М.:

Просвещение, 2011. – с. 277 – 286.

23.       Примерные прогр аммы по учеб  ным предметам. Матем атика. 5-9.

–   М.: Просве щение, 2011. – с. 3-4

24.       Приме рные программы п о учебным предм етам. Математика. 5-9.

–   М.: Просвещение, 2011. – с. 6-7

25.       Примерные прогр аммы по учеб  ным предметам. Матем атика. 5-9. – М.: Просве щение, 2011. – с. 18-23, с.40-45

26.       Е.С. Савинов Приме рная основная образова  тельная программа образова тельного учреждения. Осно вная школа / по д ред. Е.С.Сави нова. –М.: Просве щение, 2011.  –  286 с.

27.       Сапе гина, И. В. Организация проц  есса обучения матем атике в 5-6 клас сах, ориентированного н а понимание [Тек  ст]: дисс. … ка нд. пед. на ук:

13.00.02 / И. В. Сапегина; Ро с. гос. пе д. ун-т им. А. И. Герц ена; науч. ру к.:  Е. И. Лященко. – СПб., 2002. – 151 с.

28.       Сара нцев, Г. И. Методика обуч  ения математике в средней шко ле [Текст]/ Г. И. Сара нцев. – М.: Просве щение, 2002. – 224 с.

29.       Стан дарт основного общ  его полного образо вания по матем атике [Текст]. – М.: Госстандарт Рос сии: Изд-в о стандартов.

30.       Тео рия и мето дика развития универс  альных учебных дейс  твий. Выпуск 1: сбор  ник материалов / По д ред. П.М. Гор  ева, В.В. Утемова; науч  ный ред. Г.А. Русс ких // Концепт. Прило жение №9. –Киров: МЦИТО, 2013. –

137 с. 

31.            Универс альные учебные дейс твия: от ид  еи – к техно логии, от це ли – к инстру менту: материалы Втор ого Всероссийского педа  гог. форума (27-29 мар та 2012 г.) – Екатер инбург: ИРО, 2012. – 232 с.

32.            Фундаментальное яд  ро содержания общ  его образования / Ро с.

акад. на ук, Рос. ак ад. образования; по д ред. В.В. Козл  ова, А. М. Кондакова. – 4-е изд., дор  аб. – М.: Прос вещение, 2011. –  36-45 c.

33.            Воло вич М. Б. Ключ к пониманию матем  атики. – М., 2007.

34.            Глей зер Г. И. История матем атики в шко ле: 4 – 6 классы: Посо бие для учит  елей. – М., Просв ещение, 2014. -364 c.

35.            Гус ев В. А. Как пом очь ученику полю бить математику. – М., 2013.

36.            Далингер В. А. Обуч ение учащихся реше нию текстовых зад  ач методом с оставления уравн ений. – Омск.: ОмГ ПУ, 2011. -144 с.

37.            Заха рова А. Е. Текстовые зад  ачи в кур  се алгебры осно вной школы. Уче бно-методические матер  иалы спецкурса п о методике препод  авания математики «Избра  нные вопросы обуч ения алгебре в основн ой школе». М.: «Прометей»,2012. -88 с.

38.            Колягин Ю. М. Зад ачи в обуч ении математик е: т.2. – М.:

Просвещение,2017. -63 с.

39.            Крутецкий В. А. Осн овы педагогической психо логии. – М.:

Просве щение,2012. -37 с.

40.            Ляще нко Е. И. Проблема зад ач в школ  ьном курсе матем атики. Задачи ка к цель и средство обуч  ения математике учащ  ихся средней шк олы. – ЛГ ПИ им. А.И. Герц ена,2013. -94 с.

41.            Матем атика в 5 клас сах:В пом ощь учителю / По д ред. А.И.

Ма ркушевича. – М.: Просвещение, 2011. - 121 с.

42.            Математика: 5-11 к л.: Программы. Темати ческое планирование: Дл я общеобразоват. ш  к., гимназий, лиц еев. /М-в о образования Р  Ф; Сост. Г. М. Кузне цова, Н. Г. Миндюк. – М.: Дро фа, 2010- 320 с.

43.            Матем атика: Учебник дл  я 5 кл. общеобр  азоват. учреждений /  Н. Я. Виле нкин, В. И. Жохов, А. С. Чесн оков, С. И. Шварцбурд. – 5-е изд., ис пр. И до п. – М.: Из дательство «Русс кое слово», 2008. – 358 с.

44.            Мухина В. С. Возра стная психология: Учеб  ник. – М.: «Акад  емия», 2010. -29 с.

45.            Оре хов Ф. А. Решение зад  ач методом состав ления уравне ний. – М.: Просве щение, 2012. -17 с.

46.            По йа Д. Ка к решать зад ачу: Пособие дл  я учителей. М., 2008. -76 с.

47.            Сара нцев Г. И. Упражнения в обучении ма  тематике. – М.:

Просвещение, 2016. -83 с.

48.            Сорокин П. И. Занимат  ельные задачи п о математике с решениями и методическими указа  ниями: Пособие д  ля учит  елей I – V кл.: 2015. -48 с.

49.            Шевкин А. В. Обуч ение решению текст  овых задач в 5 – 6 классах. – М.: Рус. сло во, 2011. -72 с.

50.            Фрид ман Л. М. Психолого-педагог  ические основы обуч ения математике в школе. – М.: Просвещение, 2016. -96 с.

51.            Фридман Л. М., Туре цкий Е.Н. Как научи ться решать зад ачи:

Пособие дл  я учащи хся. – М.: Просве щение, 2011. -26 с.

ПРИЛО ЖЕНИЕ Приложение А

Технологическая кар  та 3

Тема комбинир ованного урока: «Реше  ние нестандартных задач, приводящихся к уравнению» 

Табл ица А.1 – Технолог ическая карта к уроку 3

Продолжение табл ицы А.1

Продолжение табл ицы А.1

Продол жение таблицы А.1

Продол жение таблицы А.1

Продолжение табл ицы А.1

Продолжение табл ицы А.1

Продол жение таблицы А.1

Продолжение табл ицы А.1

Продолжение табл ицы А.1

           Продол жение таблицы А.1                                                                                                                     

Продолжение табл ицы А.1

Приложение Б

Материалы по апробации результатов исследования:

-   Справка об апробации;

81