Решение задач математики и информатики с помощью графов

Теоретическая часть

Впервые основы теории графов появились в 1736 г. в работе Леонарда Эйлера, где он описывал решения головоломок и математических развлекательных задач. Широкое развитие теория графов получила с 50-х гг. ХХ в. в связи со становлением кибернетики и развитием вычислительной техники. Итак, дадим определение графа.

Графом в математике называется конечная совокупность точек, именуемых вершинами; некоторые из них соединены друг с другом линиями, называемыми ребрами графа. Существует несколько разновидностей графов: ориентированный граф(орграф), неориентированный граф и взвешенный граф.

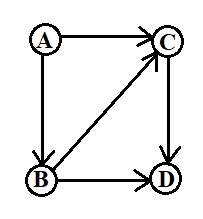Ориентированный граф-это граф, рёбрам которого присвоено направление.

	A	B	C	D
A	0	1	1	0
B	0	0	1	1
C	0	0	1	1
D	0	0	0	0

 

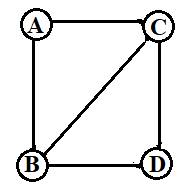Неориентированный граф-это граф, в котором нет направлений линий.

	A	B	C	D
A	0	1	1	0
B	0	0	1	1
C	0	0	1	1
D	0	0	0	0

 

Взвешенный граф-это граф, рёбра которого имеют «вес», то есть длину.

 

	A	B	C	D
A		10	7	0
B	10		5	6
C	7	5		3
D	0	6	3

 

 

 

 

 

 

 

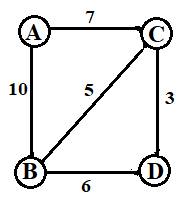
Графы достаточно часто можно встретить в окружающем нас мире, к примеру, схема движения поездов метрополитена или маршрутных такси, генеалогическое древо, созвездия и прочее.

 

Решение задач с помощью графов

Теперь переедем от теории к практике и рассмотрим применение графов к решению задач.

Задача 1.

Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?

Решение

Итак, имеется 5 человек. Выберем пять произвольных точек плоскости, которые назовём по первой букве имени мужчины. Эти точки будут являться вершинами графа, а отрезки, соединяющие данные вершины, будут представлять собой рукопожатия, которые произвели между собой мужчины.

 

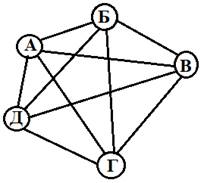
Если подсчитать число ребер графа, изображенного на рисунке, то это число будет равно количеству совершенных рукопожатий. Как видно, их 10.

Ответ:10

Задача 2

В одном дворе живут четыре друга. Вадим и шофер старше Сергея, Николай и слесарь занимаются боксом, электрик-младший из друзей. По вечерам Андрей и токарь играют в домино против Сергея и электрика.

Определите профессию каждого из друзей

Решение

Составим граф из восьми вершин, четыре из которые будут представлять собой друзей и названы по первой букве их имени, а другие четыре вершины будут представлять собой профессии и также будут названы по первой букве.

Будем выделять два вида рёбер: красного и чёрного цвета. Красные рёбра будут обозначать, что данный человек не может иметь выбранную профессию, а чёрные рёбра будут означать, что это профессия данного человека. Если от одной вершины уже выходить три красных  ребра, то четвёртое обязательно должно быть чёрным.

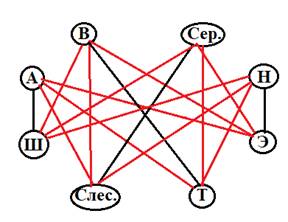
Итого, из графа получается, что Андрей-шофёр, Сергей-слесарь, Николай-электрик, Вадим-токарь.

Ответ: Андрей-шофёр, Сергей-слесарь, Николай-электрик, Вадим-токарь

Задача 3

На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.

Решение

В данной задаче есть два типа отношений «выше» и «ниже», поэтому для её решения будем применять ориентированный граф. Направление рёбер выберем следующим образом: стрелки будут иметь направление от более высокого  дерева к более низкому..

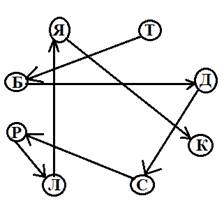
Ответ: Клен, яблоня, лиственница, рябина, сосна, дуб, береза и тополь.

Задача 4

У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо?

Решение

Составим граф в виде дерева, который будет отражать все возможные варианты исхода данного события.

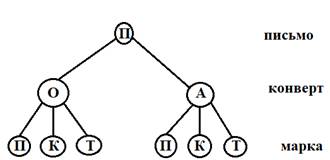
Итого, на последнем этапе получаем 6 возможных способов выбора марки.

Ответ: 6 способов

Задача 5

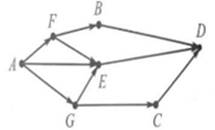
На рисунке представлена схема соединений, связывающих пункты A,F,G,B,E,C,D. По каждому соединению можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта A в пункт D?

Решение

Перестроим данный ориентированный граф в виде дерева.

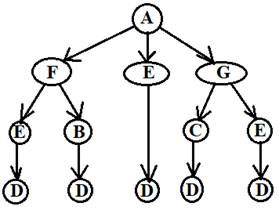
Итого, получаем 5 возможных путей из пункта А в пункт D.

Ответ: 5 путей

	A	B	C	D	E
A		1
B	1		2	2	7
C		2			3
D		2			4
E		7	3	4

Задача 6

Между населенными пунктами A,B,C,D,E построены дороги. Необходимо определить длину кратчайшего пути между пунктами А и Е. Передвигаться можно только по дорогам, протяжённость которых представлена в таблице.

Решение

Перед нами взвешенный граф, представленный в виде таблицы, перестроим его в виде схемы.

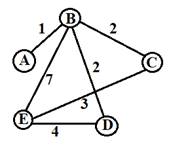
Из рисунка видно, что длина кратчайшего пути между пунктами А и Е равна 6(путь АВСЕ).

Ответ: 6

Задача 7

В первенстве класса по настольному теннису 6 участников: Андрей, Борис Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной и  Еленой; Борис – с Андреем, Галиной; Виктор – с Галиной, Дмитрием и  Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько еще осталось?

Решение

Построим граф, вершинами которого будут являться участники турнира. Красным цветом обозначим те партии, которые были сыграны, а чёрным-все оставшиеся свободные партии.

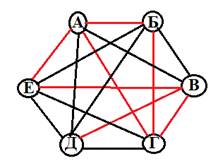
Получаем, что сыграно было 7 партий, а осталось сыграть 8.

Ответ: проведено 7 игры, осталось 8.

Задача 8

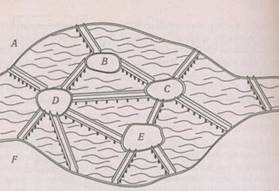
Четыре острова соединены между собой и с берегами реки 14 мостами так, как это показано на рисунке. Можно ли за одну прогулку обойти все эти мосты, побывав на каждом из них один раз?

Решение

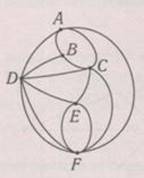Построим граф. Имеются две нечетные вершины В и С. Следовательно за одну прогулку можно обойти все мосты, побывав на каждом из них один раз. При этом прогулку надо начинать с острова В и заканчивать на острове С или наоборот.

Ответ: да, можно

Задача 9

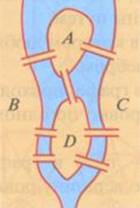Рукава реки Прегель, на берегу которой расположен город Кенигсберг, образовывали два острова. В эту эпоху четыре образовавшихся участка суши (правый и левый берег и два острова) соединяло семь мостов так, как это показано на рисунке. Горожане, гуляя по городу, пытались составить маршрут, чтобы он проходил по каждому мосту ровно один раз.

Решение

Эту задачу решил Леонард Эйлер. Он построил следующий граф и получил, что все четыре вершины нечетные, то есть нельзя пройти по всем мостам один раз и закончить путь там, где он был начат.

Ответ: данный маршрут невозможен

Задача 10

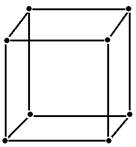Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все 12 ребер куба, не проходя дважды по одному ребру? Подпрыгивать и перелетать с места на место не разрешается

Решение

Ребра и вершины образуют граф, все 8 вершин которого имеют 3 степень, и, следовательно, требуемый обход невозможен.

Ответ: невозможно

 

 

Задача 11

Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?

Решение

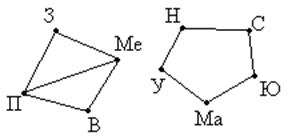Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.

Ответ: нельзя

Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.

Рассмотрим одну из таких задач

 Задача 12

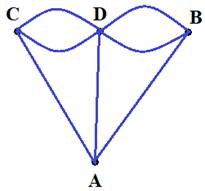
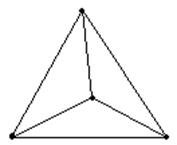
Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?

Решение

Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.

Ответ: нельзя.

Задача 13

4 человека из нашего класса захотели поздравить друг друга с новым годом. Сделать это решили с помощью SMS-ок. Сколько всего SMS-ок было отправлено?

Решение

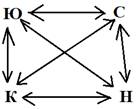
Ответ: 12

Задача 14

Клоуны Бам, Бим, Бом вышли на арену в красной, синей и зеленой рубашках. Их туфли тоже были этих  трех цветов. Туфли и рубашка Бима были одного цвета. На Боме не было ничего красного. Туфли Бама были синие, а рубашка нет. Каких цветов были туфли и рубашка у Бома и Бима?

Решение

Рубашка Бама синяя, а Бома — зелёная. Туфли Бома не могут быть ни красными, ни зелёными (ибо зелёные туфли у Бама). Поскольку туфли Бама зелёные, то туфли Бома не могут быть ни красными, ни зелёными. Значит, они синие. Биму остаются красные туфли. Поэтому и рубашка у него красная. Тогда рубашка Бама синяя, а Бома — зелёная. Изобразим с помощью графа

Ответ: Бом – синяя рубашка и зеленые туфли. Бам – зеленая рубашка и синие туфли.

Задача 15

В школьной столовой на первое можно заказать щи, суп и борщ, на второе – котлету и рыбу, а на третье – чай и морс. Сколько различных обедов можно составить из указанных блюд?

Решение

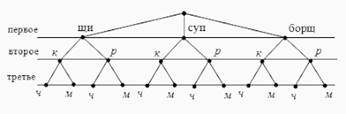
Ответ: 12 обедов

Задача 16

Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам?

Решение

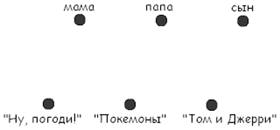Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками

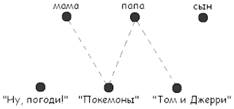Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует – то штриховой. Заметим, что по условию задачи у человека только один любимый мультфильм. Учитывая данные задачи, получаем следующую схему:

Из условия задачи следует, что нужно найти единственно возможное соответствие между элементами двух множеств.

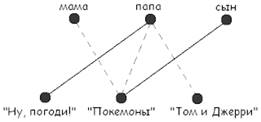
Поэтому граф на рисунке будет выглядеть следующим образом:

Ответ:  папа любит мультфильм «Ну, погоди!», сын – «Покемоны», а мама любит мультфильм «Том и Джерри».

Задача 17

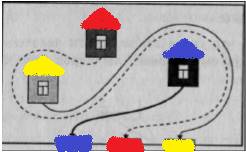
Во дворе, который окружен высоким забором, находятся три домика:

красный, желтый и синий. В заборе есть три калитки: красная, желтая и

синяя. От красного домика проведите дорожку к красной калитке, от желтого

домика – к желтой калитке, от синего – к синей так, чтобы эти дорожки не

пересекались.

Решение

Задача 18

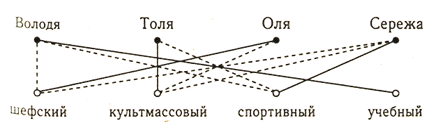
Четыре одноклассника - Володя, Толя, Оля и Сережа выбраны классным собранием для работы в шефском, культурно-массовом, спортивном и учебном секторах школы. Определите, кого из ребят в какой из названных секторов выбрали, если известно, что:

1) Володя и культсектор живут в одном доме, и они вместе с Олей втроем ездят в школу на автобусе;

2) на классном собрании было решено в спортсектор избрать мальчика;

3) учебный сектор и Сережа вместе ходят на теннисный корт;

4) спортсектор и Володя - большие друзья;

5) Оля сидит за одной партой с учебным сектором.

Решение

Составим граф из множества ребят и множества секторов

 

	Шефский сектор	Культмассовый сектор	Спортивный сектор	Учебный сектор
Володя	-	-	-	+
Толя	-	+	-	-
Оля	+	-	-	-
Сережа	-	-	+	-

Ответ: Володя -  учебный сектор, Толя -  культмассовый сектор, Оля-шефский сектор, Серёжа – спортивный сектор.

Задача 19

В пяти корзинах лежали яблоки пяти разных сортов. Яблоки первого сорта лежат в корзинах Г и Д; яблоки второго сорта - в корзинах А, Б, Г; в корзинах А, Б, В имеются яблоки пятого сорта, в корзине В имеются к тому же яблоки четвертого сорта, а в корзине Д - третьего. Пронумеруйте каждую корзину так, чтобы в корзине №1 были яблоки первого сорта (хотя бы одно); в корзине №2 - второго и т.д.

Решение

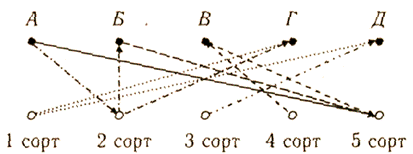
Ответ: №1 - Г;  №2 - А или №2 - Б;  №3 - Д; №4 - В;  №5 - Б или №5 - А.

Задача 20

В стране Семёрка 15 городов, каждый из которых соединён дорогами не менее, чем с семью другими. Докажите, что из каждого города можно добраться до любого другого (возможно, проезжая через другие города).

Решение

Рассмотрим два произвольных города и предположим, что они не соединены путем, то есть такой последовательностью дорог, в которой начало очередной дороги совпадает с концом предыдущей. Каждый из этих двух городов по условию соединен не менее, чем с семью другими; при этом все упомянутые города различны – ведь если какие-то два из них совпадают, то есть путь, соединяющий исходные города. Таким образом, мы насчитали не менее 16 городов. Противоречие.

Задача 21

Дима, приехав из Врунляндии, рассказал, что там есть несколько озер, соединённых между собой реками. Из каждого озера вытекают три реки, и в каждое озеро впадают четыре реки. Докажите, что он ошибается.

Решение

Общее количество "втекающих" рек должно быть равно общему количеству "вытекающих" рек. То есть возникает противоречие.

Задача 22

Несколько Совершенно Секретных Объектов соединены подземной железной дорогой таким образом, что каждый Объект напрямую соединён не более чем с тремя другими и от каждого Объекта можно добраться под землей до любого другого, сделав не более одной пересадки. Каково максимальное число Совершенно Секретных Объектов?

Решение

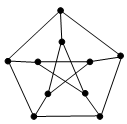Из данного Объекта можно добраться за один "ход" до трёх Объектов, а с пересадкой – еще до  2·3 = 6 Объектов. Следовательно, Объектов не больше 10. Пример такого графа с 10 объектами изображен на рисунке.

Ответ: 10 объектов

Задача 23

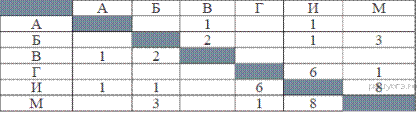Иван-Царевич спешит выручить Марью-Царевну из плена Кощея. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого длинного участка кратчайшего пути от Ивана-Царевича до Марьи-Царевны (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице:

Решение

Построим граф, соответствующий данной таблице

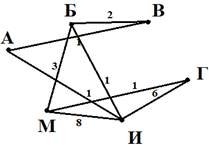
Ответ: 3

Задача 24

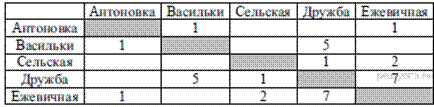Учитель Иван Петрович живёт на станции Антоновка, а работает на станции Дружба. Чтобы успеть с утра на уроки, он должен ехать по самой короткой дороге. Проанализируйте таблицу и укажите длину кратчайшего пути от станции Антоновка до станции Дружба:

Решение

Построим граф, соответствующий данной таблице

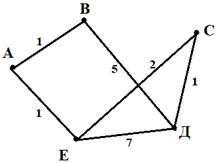
Ответ: 4

Задача 25

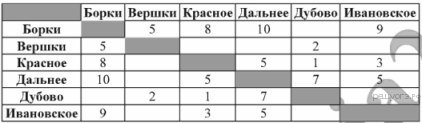Сельская малокомплектная школа находится в поселке Вершки. Петя Орлов живёт в деревне Дальнее. Определите, какое минимальное расстояние ему надо пройти, чтобы добраться до школы:

Решение

Построим граф, соответствующий данной таблице

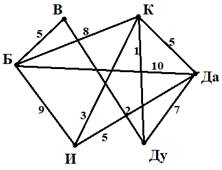
Ответ: 8

Задача 26

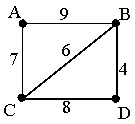На схеме нарисованы дороги между четырьмя населёнными пунктами A, B, C, D и указаны протяжённости данных дорог.

Определите, какие два пункта наиболее удалены друг от друга (при условии, что передвигаться можно только по указанным на схеме дорогам). В ответе укажите кратчайшее расстояние между этими пунктами.

Решение

Заметим, что наиболее удалены друг от друга пункты A и D. Найдём все варианты маршрутов из A в D и выберем самый короткий.

A—B—D: длина маршрута 13 км.

A—C—D: длина маршрута 15 км.

A—B—C—D: длина маршрута 23 км.

A—C—B—D: длина маршрута 17 км.

Заметим, что кратчайшее расстояние между пунктами A и D равняется 13.

Ответ: 13

Задача 27

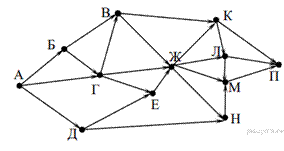На рисунке— схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город П, проходящих через город Л?

Решение

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город. С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

А = 1.  Б = А = 1.  Г = А + Б = 2.  Д = А = 1.  В = Б + Г = 3.  Е = Г + Д = 3.

Ж = В + Г + Е = 8.  К = Ж + В = 11.  Л = Ж + К= 19.  Н = Д + Ж = 9.

М = Л = 19 (Ж и Н не учитываем, поскольку путь должен проходить через Л). П = Л + М = 38 (К не учитываем, поскольку путь должен проходить через Л).

Ответ: 38

Задача 28

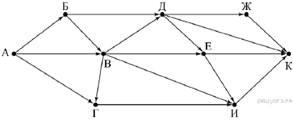На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт К, не проходящих через пункт В?

Решение

Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

А = 1.  Б = А = 1.  Г = А = 1.  Д = Б = 1.

Е = Д = 1 (В не учитываем, поскольку путь не должен проходить через город В).

Ж = Д = 1.  И = Г + Е = 2.  К = Ж + Е + И + Д = 5.

Ответ: 5

Задача 29

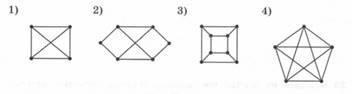Для графов,представленных на рисунке, укажите количество вершин и количество рёбер.

Решение

	Количество вершин	Количество рёбер
Фигура 1	4	6
Фигура 2	6	8
Фигура 3	8	12
Фигура 4	5	10

 

Задача 30

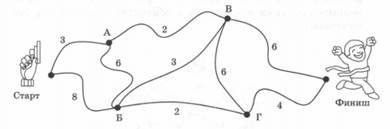На соревнованияхпо спортивному ориентированию участник должен пробежать от старта до финиша, набрав максимально возможное количество баллов (их число за преодоление того или иного участка указано на рисунке). Определите это количество.

Решение

Рассмотрим все возможные пути:

С-А-В-Ф=3+2+6=11

С-Б-Г-Ф=8+2+4=14

С-А-Б-Г-Ф=3+6+2+4=15

С-А-Б-В-Ф=3+6+3+6=18

С-А-Б-В-Г-Ф=3+6+3+6+4=22

С-Б-А-В-Г-Ф=8+6+2+6+4=26

С-Б-В-Г-Ф=8+3+6+4=21

Ответ: 26

 

 

Скачано с www.znanio.ru