РЕШЕНИЕ ЗАДАЧ, СВЯЗАННЫХ

Решение задач, связанных
с физическими величинами

Цели: продолжить формировать умение представлять числа в стандартном виде; формировать умение сравнивать числа, представленные в стандартном виде; формировать умение решать задачи, связанные с физическими величинами.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Назовите число в стандартном виде:

а) 608,5;        б) 0,083;        в) 400;        г) 0,0009;        д) 1,367;        е) 2.

2. При каком значении п верно равенство:

а) 32,4 · 10^п = 0,00324;

б) 0,072 · 10^п = 7,2;

в) 4 · 10^п = 4.

III. Проверочная работа.

В а р и а н т  1

1. Запишите в стандартном виде число:

а) 70000;                         д) 28 · 10⁵;

б) 60,3;                            е) 563 · 10^–4;

в) 14200,5;                      ж) 0,031 · 10⁶;

г) 0,56;                             з) 0,0077 · 10^–2.

2. Выполните действия:

а) (1,5 · 10^–3) · (9,2 · 10^–4);

б) (1,56 · 10^–2) : (2,6 · 10^–6);

в) 5,1 · 10⁵ + 2,9 · 10⁶.

В а р и а н т  2

1. Запишите в стандартном виде число:

а) 900000;                      д) 47 · 10⁴;

б) 800,5;                          е) 672 · 10^–5;

в) 2400,8;            ж) 0,0055 · 10⁷;

г) 0,73;                             з) 0,046 · 10^–3.

2. Выполните действия:

а) (7,8 · 10^–4) · (3,5 · 10^–6);

б) (3,36 · 10^–3) : (4,8 · 10^–7);

в) 5,2 · 10⁴ + 2,8 · 10⁵.

Р е ш е н и е

В а р и а н т  1

1. а) 70000 = 7 · 10⁴;                                        д) 28 · 10⁵ = 2,8 · 10⁶;

    б) 60,3 = 6,03 · 10;                                        е) 563 · 10^–4 =5,63 · 10^–2;

    в) 14200,5= 1,42005 · 10⁴;               ж) 0,031 · 10⁶ = 3,1 · 10⁴;

    г) 0,56 = 5,6 · 10^–1;                                        з) 0,0077 · 10^–2 = 7,7 · 10^–5.

2. а) (1,5 · 10^–3) · (9,2 · 10^–4) = (1,5 · 9,2) · (10^–3 · 10^–4) = 13,8 · 10^–7 =

        = 1,38 · 10 · 10^–7 = 1,38 · 10^–6;

    б) (1,56 · 10^–2) : (2,6 · 10^–6) = (1,56 : 2,6) · (10^–2 : 10^–6) = 0,6 · 10⁴ =

         = 6 · 10^–1 · 10⁴ = 6 · 10³;

    в) 5,1 · 10⁵ + 2,9 · 10⁶ = 0,51 · 10⁶ + 2,9 · 10⁶ = 10⁶ (0,51 + 2,9) =

         = 3,41 · 10⁶.

В а р и а н т  2

1. а) 900000 = 9 · 10⁵;                                      д) 47 · 10⁴ = 4,7 · 10⁵;

    б) 800,5 = 8,005 · 10²;                                  е) 672 · 10^–5 = 6,72 · 10^–3;

    в) 2400,8 = 2,4008 · 10³;                              ж) 0,0055 · 10⁷ = 5,5 · 10⁴;

    г) 0,73 = 7,3 · 10^-1;                                        з) 0,046 · 10^–3 = 4,6 · 10^–5.

2. а) (7,8 · 10^–4) · (3,5 · 10^–6) = (7,8 · 3,5) · (10^–4 · 10^–6) = 27,3 · 10^–10 =

        = 2,73 · 10 · 10^–10 = 2,73 · 10^–9;

    б) (3,36 · 10^–3) : (4,8 · 10^–7) = (3,36 : 4,8) · (10^–3 : 10^–7) = 0,7 · 10⁴ =

        = 7 · 10^–1 · 10⁴ = 7 · 10³;

    в) 5,2 · 10⁴ + 2,8 · 10⁵ = 0,52 · 10⁵ + 2,8 · 10⁵ = 10⁵ (0,52 + 2,8) =

        = 3,32 · 10⁵.

IV. Формирование умений и навыков.

На этом уроке учащиеся должны сравнивать и упорядочивать числа, записанные в стандартном виде, переходить от одних единиц измерения к другим, округлять числа.

1. Сравните числа:

а) 1,78 · 10⁶ и 2,1 · 10⁶;

б) 3,9 · 10^–8 и 6,5 · 10^–8;

в) 8,3 · 10⁴ и 1,4 · 10⁵;

г) 4,7 · 10^–7 и 5,8 · 10^–8.

При решении этих упражнений выводим свойство, что удобно сравнивать  числа одного порядка. Если числа разного порядка, то больше то число, порядок которого больше.

Р е ш е н и е

а) 1,78 < 2,1, значит, 1,78 · 10⁶ < 2,1 · 10⁶.

б) 3,9 < 6,5, значит, 3,9 · 10^–8 < 6,5 · 10^–8.

в) Порядок числа 1,4 · 10⁵ больше порядка числа 8,3 · 10⁴, значит,
1,4 · 10⁵ > 8,3 · 10⁴.

г) Порядок числа 4,7 · 10^–7 больше порядка числа 5,8 · 10^–8, значит,
4,7 · 10^–7 > 5,8 · 10^–8.

2. Порядок числа а равен –12. Каков порядок числа:

а) 100а;          б) 0,001а;          в) а · 10¹⁵;          г) ?

Р е ш е н и е

Так как порядок числа а равен –12, то его стандартный вид b · 10^–12, где 1 ≤ b < 10, тогда:

а) 100а = 100 · b · 10^–12 = b · 10² · 10^–12 = b · 10^–10, порядок числа равен –10.

б) 0,001а = 0,001 · b · 10^–12 = b · 10^–3 · 10^–12 = b · 10^–15, порядок числа равен –15.

в) а · 10¹⁵ = b · 10^–12 · 10¹⁵ = b · 10³, порядок числа равен 3.

г) 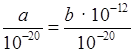 = b · 10^{–12 + 20} = b · 10⁸, порядок числа равен 8.

О т в е т: а) –10; б) –15; в) 3; г) 8.

3. № 1021.

Р е ш е н и е

Формула пути S = V · t;

t = 2,8 · 10⁶ (с);    V = 3 · 10⁵ (км/с);

S = (2,8 · 10⁶) · (3 · 10⁵) = 8,4 · 10¹¹ (км).

О т в е т: 8,4 · 10¹¹ (км).

4. № 1022.

Р е ш е н и е

т_З = 6,0 · 10²⁴ кг;   т_М = 6,4 · 10²³ кг.

Порядок т_З больше порядка т_М, значит, масса Земли больше массы Марса. Чтобы узнать во сколько раз больше, найдём частное:

.

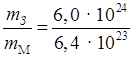
О т в е т: масса Земли больше массы Марса в ≈ 9,4 раза.

5. № 1024.

Р е ш е н и е

ρ = 7,8 · 10³ кг/м³;   ρ = ;   m = ρ · V.

Найдём объём железной пластины:

V = 1,2 · 6 · 10^–1 · 2,5 · 10^–1 = 18 · 10^–2 = 1,8 · 10^–1 (м³);

т = 7,8 · 10³ · 1,8 · 10^–1 = 14,04 · 10² = 1,404 · 10³ (кг).

О т в е т: 1,404 · 10³ кг.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Какую запись числа называют его стандартным видом?

– Покажите на примере, как представить число в стандартном виде.

– Как сравнивают числа одного порядка?

– Как сравнивают числа разного порядка?

– Какие физические величины выражают числами стандартного вида? Приведите примеры.