РЕШЕНИЕ ЗАДАЧ4

РЕШЕНИЕ ЗАДАЧ

 Цели: повторить и обобщить изученный материал; выработать умение учащихся применять изученные теоремы при решении задач; развивать логическое мышление учащихся; подготовить учащихся к контрольной работе.

I.  Актуализация опорных знаний учащихся.

1. Проверка доказательства теоремы о соотношениях между сторонами и углами треугольника и теоремы о неравенстве треугольника (у доски и за первыми партами - на листочках; это позволяет проверить у учащихся знание теорем и накопить отметки).

2. Фронтальная работа с классом:

1) ответы на вопросы 1-9 на с. 89-90;

2) устно решить задачу: существует ли треугольник со сторонами 4 м, 5 м и 8 м; со сторонами 6 см, 12 см и 3 см; со сторонами 9 дм, 9 дм и 7 дм?

3. Собрать листочки у работающих на месте и выслушать ответы учащихся, работающих у доски.

II. Решение задач.

1. Решить задачу № 243 на доске и в тетрадях.

Дано: ΔABC; АА1 - биссектриса; СД || АА1 и Д ∈ АВ.

Доказать: АС = АД.

Доказательство: Так как по условию АА1 - биссектриса треугольника ABC, то ∠1 = ∠2.

∠1 = ∠4 как накрест лежащие углы при пересечении параллельных прямых АА1 и СД и секущей АД. Из равенств ∠1 = ∠2; ∠1 = ∠4; ∠2 = ∠3 следует, что ∠3 = ∠4, тогда по признаку равнобедренного треугольника имеем, что треугольник ДАС - равнобедренный, значит, по определению АС = АД.

2. Решить задачу 1: в прямоугольном треугольнике ABC гипотенуза АВ = 10 см. Найдите СД, если точка Д лежит на гипотенузе АВ и ВД = СД.

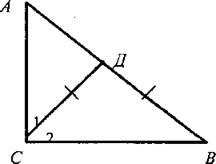Дано: ДABC; ∠С = 90°; АВ = 10 см. Д ∈ АВ и ВД = СД

Найти: СД.

Решение: ∠2 = ∠5, так как по условию СД = ДВ. ∠1 + ∠2 = 90°; ∠В + ∠А = 90°; но ∠2 = ∠В, поэтому ∠А = ∠1, значит, треугольник АДС - равнобедренный, тогда АД = СД.

Итак, СД = ВД по условию, АД = СД по доказанному, следовательно, СД = 1/2АВ = 5 см.

Ответ: 5 см.

3. Решить задачу 2: отрезок ЕК — биссектриса треугольника ДЕС.

Докажите, что КС < ЕС.